Sample Paper ICSE Class 10 Mathematics Set C

Students can refer to the following Sample Paper ICSE Class 10 Mathematics Set C with Answers provided below based on the latest syllabus and examination guidelines issued for ICSE Mathematics. All specimen papers have been prepared covering all chapters given in ICSE Mathematics book for Class 10. You should also refer to ICSE Class 10 Mathematics Solutions.

Sample Paper ICSE Class 10 Mathematics Set C with Answers

ICSE CLASS 10
MATHEMATICS
SAMPLE PAPER

General Instructions:
1. Answers to this paper must be written on the paper provided separately.
2. You will not be allowed to write during the first 15 minutes. Utilize that time in reading the Question Paper.
3. The time given at the head of this paper is the time allowed for writing the answers.
4. Attempt all questions from Section A and any four questions from Section B.
5. All working, including rough work, must be clearly shown, and must be done on the same sheet as the rest of the answers.
6. Omission of essential working will result in loss of marks.
7. The intended marks for questions or parts of questions are given in brackets [ ].
8. Mathematical tables are provided.

Question 1
a) Solve the following inequation, write the solution set and represent it on the number line.

b) An AP consists of 29 terms. The sum of 3-middle most terms is 375 and the sum of the last 3-terms is 531. Find the AP. [3]
c) Prove the following identity – (cos𝜃− cosec𝜃)² + (sin𝜃− sec𝜃)² = (1 – sec𝜃cosec𝜃)²

Question 2
a) R₁ and R₂ are the remainder when the polynomial x³ + 2x² – 5ax – 7 and x³ + ax² – 12x + 6 are divided by x + 1 and x – 2 respectively. If 2R₁ + R₂ = 6, find the value of a. [3]
b) Prove: cos⁴A – cos²A = sin⁴A – sin²A [3]
c) 200 logs are stacked one over the other, 20 logs in bottom row, 19 in the next row, 18 in the row next to it and so on. In how many rows 200 logs are placed and how many logs are there in the top row.

Question 3
a) Find a, b, c, d: If 3

b) If A (−2, −1), B (a, 0), C (4, b) and D (1, 2) are vertices of a parallelogram, find the value of a and b. [3]
c) A girl fills a cylindrical bucket 32 cm in height and 18 cm in radius with sand.
She empties the bucket on the ground and makes a conical heap of the sand.
If the height of the conical heap is 24 cm, find:
i) its radius
ii) its slant height

Question 4
a) If b is the mean proportional between a and c, prove that :
abc (a + b + c)³ = (ab + bc + ca)³ [3]
b) Solve the quadratic equation and give your answer to two significant digits:
5x (x + 2) = 3 [3]
c) Find the co-ordinates of the points of trisection of the line segment joining the points A (5, -3) and B (2, -9).

SECTION B (40 marks)
(Attempt any four questions from this section.)

Question 5
a) A box contains 90 discs which are numbered from 1 to 90. If one disc is drawn at a random from the box, find the probability that it bears:
i) A two – digit number
ii) A perfect square number
iii) A number divisible by 5

b) Mr. Gupta opened a Recurring Deposit Account in a bank. He deposited ₹ 2500 per month for 2 years. At the time of maturity, he gets ₹ 67500. Find the rate of interest per annum.

c) Using a graph paper, plot A (4,6) and B (1,2).
i) Reflect A in X – axis to get the images A’.
ii) B’ is the image of B, when reflected in line AA’.
iii) Give the geometrical name for the figure ABA’B’.
iv) Find the area of figure A’B’B.

Question 6
a) On a map drawn to a scale of 1 : 50000, a rectangular plot of land ABCD has the following dimensions. AB = 6 cm; BC = 8 cm and all angles are right angles. Find:
i) The actual length of diagonal distance AC of the plot in km.
ii) The actual area of the plot in sq. km. [3]

b) From a circular cylinder of diameter 10 cm and height 12 cm, a conical cavity of the same base radius and of the same height is hollowed out. Find the volume and the whole surface of the remaining solid. (Take 𝜋 = 3.14) [3]

c) A solid is in the form of a cylinder with hemispherical ends, the total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the volume and total surface area of the solid.

Question 7
a) Find the intercepts made by the line 2x – 3y + 12 = 0 on the coordinate axis. [3]
b) Prove: 2sec²A – sec⁴A – 2cosec²A + cosec⁴A = cot⁴A – tan⁴A [3]
c) Given matrix A =c

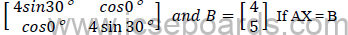
i) Write the order of matrix X.
ii) Find the matrix X.

Question 8
a) Which term of A.P. 3, 15, 27, 39, . . . . . . will be 120 more than its 21st term? [3]
b) If the median of 24, 27, 28, 31, 34, x, 37, 40, 42, 45, is 35, find x. In these data, if 45 is changed to 33, find the new median. [3]
c) A boat goes 12 km downstream and returns moving upstream to the same spot after 4 1/2 hours. The speed of the current is 2 km/h. Find the speed of the boat in still water.

Question 9
a) Using componendo and dividendo, find the value of x :
√3𝑥 + 4 + √3𝑥 − 5/ √3𝑥 + 4 − √3𝑥 − 5 =9

b) If the image of the point A (2, 1) with respect to the mirror line be A’ (5, 2), find the equation of the mirror line. [3]
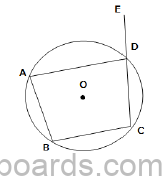
c) In the given figure, ABCD is a quadrilateral, inscribed in a circle with centre O. Side CD is produced to E. If ADE = 95⁰ and ∠OBA = 30⁰, find: [4]
i) ∠OBC
ii) ∠OAC

Question 10
a) Prove that tan𝜃+sec𝜃−1/tan𝜃−sec𝜃+1=1+sin𝜃/cos𝜃
b) The monthly income of a group of 320 employees in a company is given below:

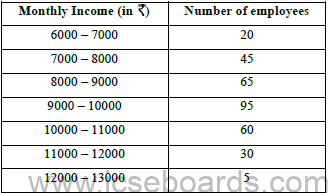
Draw an ogive for the given distribution on a graph sheet taking 2 cm = 1000 on one axis and 2 cm = 50 employees on the other axis. From the graph determine:
i) The median wage. ii) The number of employees whose income is below 8500. iii) If the salary of a senior employee is above 11500, find the number of senior employees of the company.
iv) The upper quartile.

Question 11
a) Divide 16 into two parts such that twice the square of the larger part exceeds the square of the smaller part by 164. [3]
b) Find the amount of bill for the following intra − state transaction of goods. The rate of GST is 12%.

c) A man from the top of a vertical tower observes a car moving at a uniform speed coming directly towards him. If it takes 12 minutes to change the angle of depression from 30⁰ to 45⁰, how soon after it, will the car reach
the tower.