Students can refer to the following Sample Paper ICSE Class 10 Mathematics Set H with Answers provided below based on the latest syllabus and examination guidelines issued for ICSE Mathematics. All specimen papers have been prepared covering all chapters given in ICSE Mathematics book for Class 10. You should also refer to ICSE Class 10 Mathematics Solutions.
Sample Paper ICSE Class 10 Mathematics Set H with Answers
Subject: Mathematics
Answers to this Paper must be written on the paper provided separately.
You will not be allowed to write during the first 15 minutes.
This time is to be spent in reading the question paper.
The time given at the head of this Paper is the time allowed for writing the answers.
Attempt all questions from Section A and any four questions from Section B.
All working, including rough work, must be clearly shown and must be done on the same
sheet as the rest of the answer. Omission of essential working will result in loss of marks.
The intended marks for questions or parts of questions are given in brackets [ ].
This paper consists of 11 questions on 6 pages.
Sample Paper ICSE Class 10 Mathematics Set H
Section A [40 Marks]
Attempt all questions
Question 1
(a) Solve the following inequation and represent the solution set on a number line.[3]

(b) Find the sum of all the 11 terms of an A.P. whose middle most term is 30.[3]

A, B, and C lie on the circle, centre O. BD is a diameter and PAT is the tangent at A. Angle ABD = 580 and angle CDB = 340
Find (a) angle ACD, (b) angle ADB, (c) angle DAT, (d) angle CAO.
Question 2
(a) If (2x3 + ax2 + bx – 2) has a factor (x+2) and leaves a remainder 7 when divided by (2x – 3) find the values of a and b. With these values of a and b, factorize the given polynomial completely.[4]
(b) Using properties of proportion, solve for x:
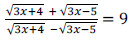

At and Bt are the transpose matrix of A and B respectively, find p and q such that A2 – 6B = I, where I is the unit matrix of the order (2×2). [3]
Question 3
(a) Shubha has a cumulative time deposit account in SBI. She deposits 800 per month for a period of 2 (1/2) years. If at the time of maturity she gets 26790, find the interest paid by the bank and hence calculate rate of interest.[3]
(b) A conical tent is to accommodate 77 people. Each person must have 16m3 of air to breathe. Given the radius of the tent is 7 m, find the height of the tent and also its curved surface area.
(c) All the three face cards of spades are removed from a pack of 52 cards and the remaining cards are well shuffled. A card is drawn at random from the remaining cards. Find the probability of getting:
i) A black face card
ii) A queen
iii) A red card
iv) The number 5
Question 4
(a) Prove that : √secA-1/secA+1 = cosecA − cot A [3]
(b) If B(9, -2) and D(5, 6) are the vertices of a parallelogram ABCD and diagonal AC is inclined at 450 with the positive direction of x-axis, find the equation of diagonal AC.
(c) Use a graph paper for this question. Take 2cm = 1 unit on both axes. [4]
Plot A (2, 3) and B (6, 3)
i) Reflect A in the origin to get the image D.
ii) Reflect A in the x-axis to get the image C.
iii) Write the co-ordinates of C and D.
iv) What kind of figure is ABCD? Find its area.
v) What is the reflection of C in y-axis?
vi) Name two points from the figure which are invariant on reflection in y-axis.
Section B
(Attempt any four questions)
Question 5
(a) In a GP the first term is 7, the last term is 448, and the sum is 989. Find the common ratio and hence find the number of terms of the series.[3]
(b) State the nature of the roots of the equation x2 – 3(x + 3) = 0 and Hence solve it correct to two significant figures.[3]
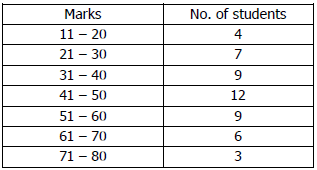
(c) Use step deviation method to find the mean of the given distribution. Also state the modal class.[4]
Question 6
(a) Given matrix A =

i) Write the order of matrix X
ii) Find the matrix X.
(b) Prove that: {tanA/1-cotA}+{cotA/1-tanA}= 1+cosecAsecA
(c) Without solving the equation (k + 1)x2 – 4kx + 9 = 0, find the value of k for which the roots are real and equal. Hence find the roots of the equation[4]
Question 7
(a) In ΔABC, D is point on side AB and E is a point on side AC. DE || BC. If AD = (4x – 3) cm, AE = (8x – 7) cm, BD = (3x – 1) cm, CE = (5x – 3) cm, find the value of x.
Hence, find area of ΔADE : area of trapezium DECB.
(b) Construct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Bisect angle C internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from line AB.
(c) Find the equation of the line perpendicular to the line containing the Points A (1, 2); B (6, 7) and passing through the point C which divides seg AB in the ratio 3:2.[3]
Question 8
(a) An aero plane travels a distance of 2400 km at a certain speed. But on the return trip due to bad weather, it reduces its speed by 50 km/hr and covers the same distance in 12 minutes more than that of onward journey. Find the original speed of the plane.[4]
(b) A mathematics aptitude test of 50 students was recorded as follows: Draw a histogram for the given data using a graph paper and estimate the mode.[3]

(c) A cylindrical can of internal diameter 12 cm contains some water. When a solid sphere of diameter 9 cm is placed in it, it is completely immersed.
Find the rise in water level, if no water overflows.[3]
Question 9
(a) If (a + 2b + c) , (a – c) and (a – 2b + c) are in continued proportion, Show that ‘b’ is the mean proportional between ‘a’ and ‘c’.[3]
(b) In the given figure, AB parallel to CD parallel to EF, AB = 5 cm, AC = 4 cm, EF = 7.5 cm, CF = x and CD = y.[4]
i) Prove that ΔFEC ∼ ΔABC
ii) Find the value of x and y
iii) Find the area ΔCDF : area ΔABF
iv) Find area ΔCDF : area trapezium ACDB

(c) Construct a triangle PQR. Given that QR = 8cm, Angle PRQ = 750 and the altitude from P on RQ is 5.6 cm. Construct circle passing through its vertices. Measure and write its radius.
Question 10[3]
(a) The top of the tower is 60 mt. high makes an angle of depression 300 and 600 with the top and bottom of the coconut tree respectively. Find the height of the tree and the distance between the bottoms of the tower and the tree.[4]
(b) The marks obtained by 200 students in an examination are given.

Using a graph paper, draw an ogive for the above distribution. Use Your ogive to estimate:
i) the Median
ii) the lower quartile
iii) the number of students who obtained more than 80% marks
in the examination and
iv) the number of students who did not pass, if the pass percentage was 35.
Question 11
(a) Mr. Vohra receives an annual income of 900 in buying 50 shares Selling at 80. If the dividend declared is 20%, find the
i) number of shares he purchased
ii) Amount invested by him to buy these shares.
iii) Percentage return on his investment to the nearest whole number.
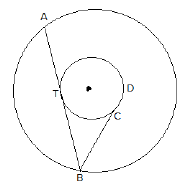
(b) The radii of two concentric circles are 9 cm and 15 cm. Tangent AB touches the smaller circle at T. Chord DC produced intersects the larger circle at B. If BD = 18 cm, find the length of BC.[3]
(c) The sum of the third term and the seventh term of an A.P. is 6 and their Product is 8. Find the sum of first 16 terms of the A.P.[3]