Students should refer to Electricity and Magnetism ICSE Class 10 Physics Board Exam Questions provided below with solutions. These will help the students to understand the type of questions which have been asked in previous year examinations and the type of solutions which the student should give to get good marks. You should also refer to ICSE Class 10 Physics Sample papers for more practice
ICSE Class 10 Physics Electricity and Magnetism Important Questions
Students should learn the important questions and answers given below for Chapter Electricity and Magnetism in Physics for ICSE Class 10. These board questions are expected to come in the upcoming exams. Students of ICSE Class 10th should go through the Important questions and answers ICSE Class 10 Physics which will help them to get more marks in exams.
Electricity and Magnetism ICSE Class 10 Physics Board Exam Questions
Electricity and Magnetism ICSE Class 10 Physics Board Exam Questions
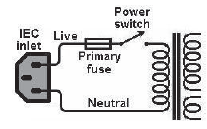
1) Why are switches always placed in the live wire?
Answer:
If the switch is connected to the neutral wire, the appliance remains connected to the live wire and is at the supply voltage even when the switch is off. Thus, the person who comes in contact with the live wire of the appliance may get a fatal shock. To avoid any accident/danger, the switch must be connected to the live wire.
2) Why do electricians use rubber gloves?
Answer:
Electricians wear rubber gloves to protect themselves from electric shocks. Rubber is a good insulator. It does not allow the current to pass through the electrician’s body and saves him from electric shocks if accidentally he touches the live wire.
3) Why is fuse always placed in the live wire?
Answer:
If the fuse is connected to the neutral wire, due to excessive flow of current, the fuse may burn and current will stop flowing in the neutral wire but the appliance will remain connected to the live wire. This means that the current keeps flowing in the appliance. In this case, if a person touches the appliance, he/she may get a severe shock.
4) Why is soft iron used as a core of the electromagnet in the electric bell?
Answer:
A soft iron used inside the coil makes the magnetic field stronger as it becomes the magnet itself when the current starts flowing. The soft iron used will lose its magnetism as soon as the current stops flowing, making it a temporary magnet. In this way, the electromagnet can be switched on and off by turning the electricity on and off. Therefore, in
an electric bell, a soft iron is used as the core of the electromagnet because it becomes magnetised and as the circuit is broken, it immediately gets demagnetised.

5) Why do we transmit alternating current at high voltage?
Answer:
Electricity transmission is done at high voltage, i.e., at low current, the energy loss due to heating (i 2 Rt) will be reduced considerably. Besides it, for low current thin wires can
be used and for thin wires less support is required, which makes the transmission economical. Therefore, the electricity generated at the powerhouse is stepped up to 11KV to
400KV or so for transmission to main substations where it is stepped down to 33KV or so. At this voltage, it is transmitted to the city substations where it is further stepped down to
220V/440V for supply to the consumer as per their requirements (domestic/commercial).
6) Why is earth pin in a plug made longer and thicker than the other two pins?
Answer:
The earth pin in a plug is made longer so that the earth connection is the first to connect and the last to disconnect. It is made thicker so that even by mistake it cannot be inserted into the live hole of the socket which may result in electric shocks.
7) Why are thick wires used in the leads of an electric radiator?
Answer:
Thick wires are used in high power instruments like electric iron, electric heater, heating rod, electric radiator because for the given voltage V,
P ∞ i
Thus, the higher is the power of the electric appliance, larger is the current drawn by it and for the given voltage V,
P ∞ 1/R,
i.e., if resistance is low, power will be more and for low resistance, the area of cross-section will be more.
8) Why is the filament of the electric iron or electric kettle put between mica sheets?
Answer:
Mica sheet provides perfect insulation on both sides of the filament and the body of electric iron or electric kettle. It allows free flow of heat.
9) Why is the bulb filled with an inert gas?
Answer:
When the current is passed through the filament, it gets heated up to about 2500 0 C due to which the filament oxidises and evaporates quickly. Thus, to prevent oxidation and evaporation of filament insert gas like Argon is filled in the bulb after evacuation, to increase its life. Argon is an inert gas which does not give rise to any chemical reaction and so would not affect the working of the tungsten filament. At the same time, the pressure of Argon gas would almost prevent ‘evaporation’ of the filament.
(image below only for reference, will not be asked in exam)

10) Why is tungsten filament used in the bulb?
Answer:
Electric bulb is based on the heating effect of the current. Tungsten filament has some amazing qualities like lower vapour pressure, greatest tensile strength out of all the metals, high resistivity, high melting point (~ 3000 0 C) and is ductile. This is why it is used as a filament in the bulb



