Students should refer to Genetics ICSE Class 10 Biology notes provided below designed based on the latest syllabus and examination pattern issued by ICSE. These revision notes are really useful and will help you to learn all the important and difficult topics. These notes will also be very useful if you use them to revise just before your Biology Exams. Refer to more ICSE Class 10 Biology Notes for better preparation.
ICSE Class 10 Biology Genetics Revision Notes
Students can refer to the quick revision notes prepared for Chapter Genetics in Class 10 ICSE. These notes will be really helpful for the students giving the Biology exam in ICSE Class 10. Our teachers have prepared these concept notes based on the latest ICSE syllabus and ICSE books issued for the current academic year. Please refer to Chapter wise notes for ICSE Class 10 Biology provided on our website.
Genetics ICSE Class 10 Biology
TOPIC-1
Definition of Genetics and Related Terms
Quick Review
➢ The term genetics was proposed by William Bateson.
➢ Genetics is the branch of biology that deals with the study of inheritance and variation of characters from parent to offsprings.
➢ The kind of transmission of characters from parent to offsprings is called heredity or inheritance. Like wise, no two individuals of a species are alike such differences are called variations.
➢ Monohybrid Cross is the inheritance of one pair of contrasting characters. For example, a cross between a pea plant with a dominant green seed and one with a recessive yellow seed.
➢ Dihybrid Cross is inheritance of two pairs of contrasting characters. For example, the inheritance of yellow and round seed character and the green wrinkled character is a dihybrid cross.
➢ Gene : Mendel presumed that a character is determined by a pair of factors present in each cell of an individual. These are known as genes in modern genetics.
➢ Allele or allelomorph : They are various forms of a gene or Mendelian factor which occurs on the same locus on homologous chromosomes and control the same character. Alleles or allelomorphs control different expressions or traits of the same character (e.g., tallness and dwarfness in Pea).
➢ Heterozygous : An individual having two contrasting Mendelian factors or genes for a character. Heterozygote or heterozygous individual is also called hybrid. E.g., Tt.
➢ Homozygous : An individual having identical Mendelian factors or genes for a character (TT or tt). Homozygous or homozygote individual is always pure for the trait.
➢ Dominant Factor : An allele or Mendelian factor which expresses itself in the hybrid ( heterozygote ) as well as in the homozygous state. It is denoted by capital letter (T for tallness)
➢ Recessive Factor : An allele or Mendelian factor which is unable to express itself in the hybrid or in the presence of alternate (dominant ) allele. It is denoted by small letter (t for dwarfness). The recessive factor expresses itself only in the homozygous state (e.g., tt ).
➢ Mutation is a new sudden inheritable discontinuous variation which appears in the organism due to the permanent change in it’s genotype.
OR
➢ Sudden changes in one or more genes in the progeny, which normally may not have existed in the parents, grand parents or even great grandparents are called mutations. For example : albinism, sickle cell Anaemia.
➢ Mutation may be of gene mutation – changes in the DNA & chromosomal mutation – changes in the number of arrangement of the chromosome.
➢ Variation : The differences among the members of same species and offspring of the same parents are referred to as variation.
OR
➢ Variation is the departure from a complete similarity between individuals of the same species.
➢ Genotype : It is the gene complement or genetic constitution of an individual with regard to one or more characters irrespective of whether the genes are expressed or not. For example, the genotype of hybrid tall pea plant is Tt, pure tall TT and dwarf tt.
➢ Phenotype : The observable, morphological or physiological expression of an individual with regard to one or more characters is called phenotype. For recessive gene, the phenotype is similar to genotype. For dominant genes, the phenotypic expression can be due to its homozygous genotype or heterozygous genotype. For example, Phenotypic tall pea plant can be genotypically TT or Tt.
TOPIC-2
Mendel’s Laws of Inheritance
Quick Review
➢ G. J. Mendel ( 1822-1884 ), the father of genetics, was an Austrian monk.
➢ He was the 1st scientist who made a systematic study of Patterns of inheritance of characters from parents to progeny.
➢ He carried out breeding experiments on garden pea plants (Pisum sativum) and formulated basic laws of heredity.
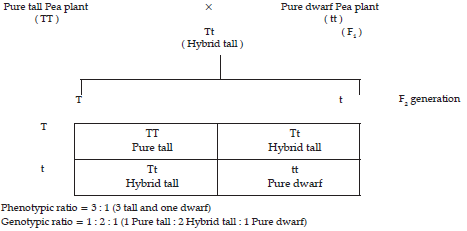
➢ Mendel crossed a pure tall garden Pea plant and a pure dwarf Pea plant, the resulting offspring were called F1 generation.
➢ Why Mendel Selected pea plant for his experiments?
(i) Garden pea has distinct, easily detectable contrasting traits
(ii) The plant reproduces will & grows to maturity in a simple season.
(iii) The Pea plant is self pollinating in nature because pea flower is bisexual.
(iv) Self pollination could be prevented by removing the male reproductive parts of the flower.
(v) Cross-pollination could be done artificially.
➢ Law of Paired Factor : A character is represented in an individual ( diploid ) by atleast two factors. The two factors lies on the two homologous chromosomes at the same locus. They may represent the same ( homozygous, e.g., TT in case of pure tall pea plant, tt in case of dwarf pea plant ) or alternate expression ( heterozygous e.g., Tt in case of hybrid tall pea plant ) of the same character.
➢Law of Dominance : In a hybrid where both the contrasting alleles or unit factors are present, only one unit factor / allele called dominant is able to express itself while the other factor / allele called recessive remains suppressed In a cross between pure breeding red flower ( RR ) Pea plant and white flower ( rr ) Pea plant, the F1 generation is red flowered though it has received both the factors ( R and r ). It is because of the dominant nature of factor for red flower colour and recessive nature of the factor for white flower colour. On self breeding, the recessive trait reappear in the F2 generation showing that it is suppressed in F1 generation and not lost.
➢Law of Segregation : Law of segregation states that the two contrasting factors do not mix in the F1 generation but segregate or separate from each other at the time of gamete formation.
➢Mendel continued his experiments further and allowed self pollination in F1 hybrids. The resultant offsprings were called F2 generation. In F2 generation tall and dwarf plants are formed in 3 : 1 ratio. So that each gamete receive only one factor, either dominant or recessive. Hence gametes are pure. Thus law of segregation is also referred to as law of purity of gametes.
➢ Law of independent assortment states that the factors of different pairs of contrasting characters behave independent to each other at the time of gamete formation, and at the time of fertilization they bring about all the possible combinations of characters.
➢ Mendel crossed a pure yellow, round seeded garden pea plant with a pure green, wrinkled seeded garden pea plant. All F1 individuals show yellow, round characters. In F1 dihybrids yellow character is dominant over green character and round character is dominant over wrinkled character.
➢ Mendel allowed self pollination of F1 dihybrids and observed F2 generation. In F2 generation, he find yellow round; yellow wrinkled; green round; green wrinkled pea plants in 9 : 3 : 3 : 1 ratio. In the above cross, in F2 generation, two more new varieties of pea plants are formed besides the parents. They are yellow, wrinkled and green, round plants.

TOPIC-3
Sex Determination in Human Beings
Quick Review
➢ In humans, 23 pair of chromosomes are present. These are classified into two main types such as – Autosomes and Sex chromosome.
➢ Autosome are 22 pairs of chromosomes other than the sex chromosomes. Autosomes are chromosomes that contain genes for anything that does not relate to sex determination.
➢ Sex chromosome is a pair of chromosome which determine the sex of a person. These XX-YY chromosomes are called hetero-chromosomes or sex chromosomes. The remaining chromosomes are called autosomes.
➢ In human beings, male gametes ( sperm ) contain either X or Y chromosome, while female gamete ( egg ) contains only X-chromosome.
➢ The sex of child depends upon the kind of sperm that fertilizes the egg during fertilization. In case, the sperm carrying ( X ) chromosome fertilizes the egg (X) then the resulting child will be female (XX) and if the sperm carrying (Y) chromosome fertilizes the egg (X) then the resulting child will be male (XY). This can be shown by the following cross:

TOPIC-4
Sex Linked Inheritance of Diseases
Quick Review
➢ Sex linked inheritance was first discovered by Morgan (1910) in Drosophila.
➢ In man , two sex linked disorders are Haemophilia and Colour blindness.
➢ In Hemophilia, blood clotting mechanism is absent. The person with colour blindness cannot distinguish colours.
➢ Hemophilia and colour blindness are caused by recessive genes present on X chromosome.
➢ The above two disorders are common in males than females, because to express disorders, two recessive genes are required for female whereas in male a single recessive gene is sufficient because its allele is absent in sex chromosomes(y).
➢ When a normal man marries a colour blind female., expected vision of their children may be shown as

Inheritance of x-liked genes as in colour blindness & haemophilia is called criss-cross inheritance. This is because the son (male) may get it from the otherwise normal but carrier mother & a colour blind father may pass it on to the daughter making her colour-blind if the mother is carrier.
Know the Terms
➢ Character : It is well defined morphological or physiological feature of an organism. eg. Stem height.
➢ Gene symbol : Each character is provided with a symbol. eg. T for tallness and t for dwarfness.
➢ Gene locus : A particular region of the chromosome representing a single gene is called gene locus.
➢ Hybrid : The heterozygous organism produced after crossing two genetically different individuals is called a hybrid .
➢ Pure line : It is a strain of true breeding individuals which have homozygous traits due to continued self breeding over the generations.
➢ Genome : It is a complete set of chromosomes where every gene and chromosome is represented singly as in a gamete.
➢ Gene pool : The aggregate of all the genes and their alleles present in a interbreeding population is known as gene pool.
➢ Backcross : It is a cross between hybrid and one of its parents in order to increase the number of traits of that parent.
➢ Test cross : It is cross between an individual with a dominant trait and a recessive organism in order to know whether the dominant trait is homozygous or heterozygous.
Genetics is the study of variations and how they are transferred from one generation to another.
Gregor Johann Mendel is considered to be the father of genetics. During his time, his findings were not accepted, but later in 1900, three scientists DeVries, Correns, and Tschermak rediscovered Mendel’s work.
The term genetics was coined by W. Batson in 1905.
Now let us explore some of the terms related to the study of genetics.
• Heredity − It is the transmission of traits from one generation to the other generation.
• Variation − It can be defined as the difference observed among members of the same species and also among offsprings of the same parent.
• Gene − A gene is the unit of inheritance, which is transferred from the parent to the offspring. It controls the expression of a character. A gene is a linear piece of DNA which is present in nucleus.
• Allelomorphs − Every character is controlled by two genes, which control contrasting expressions. A pair of genes that controls the contrasting characters and lies on the same loci in the homologous chromosomes is called an allele.
• Dominant allele − An allele which expresses itself in the presence of its contrasting allele is called a dominant allele. For example, the character tallness is determined by two alleles T and t, where T is the dominant allele and t is the recessive allele. In the presence of T, the expression of t does not occur.
• Recessive allele − The allele which cannot express itself in the presence of the dominant allele is called a recessive allele.
• Homozygous organism − In an individual, if the alleles of a character are similar, then they are known as homozygous. For example, TT is a homozygous condition.
• Heterozygous organisms − If the alleles of a character are dissimilar, then they are called heterozygous. For example, Tt is a heterozygous condition.
• Phenotype − It is the physical expression of a character. E.g., tall plant
• Genotype − It represents how an organism is genetically made up. For e.g., TT or Tt or tt
• F1 generation − It is the first filial generation which is produced when two pure parents are crossed. For example, the F1generation produced when two pure line plants TT and tt are crossed is Tt.
• F2 generation − It is the second filial generation of progeny formed when two F1 generation plants are crossed.
Mendel and His Experiments
The individuals of a family (parents and offspring) have more similarity in comparison to others. This is because certain characteristics are passed from the parents to the off springs without any variation.
Heredity is defined as the transmission of characteristics from one generation to another. These characteristics may be physical, mental, or physiological.
Commonly observed heritable features are curly hair, a particular type of ear lobe, hair on ears etc.
Transmission of traits from the parents to progeny – Mendel’s Work
Gregor Johann Mendel (1822 – 1884) was the first to carry out the study on the transmission of characteristics from the parents to the offsprings. He proposed that heredity is controlled by factors, which are now believed to be segments of chromosomes or genes.
Mendel performed experiments on a garden pea (Pisum sativum) with different visible contrasting characters. He selected seven contrasting pairs of characters or traits in a garden pea.
These include round/wrinkled seeds, tall/short plants, green/yellow pod colour, purple/white flower colour, axial/terminal flower, green/yellow seed colour, and inflated/pinched ripe pods.
Mendel’s experiment
Mendel performed experiments in three stages:

Selection of parents: Mendel selected true breeding pea plants with contrasting characteristics for his experiment.
True breeding plant is the one that produces an offspring with the same characteristics on self- pollination. For example, a tall plant is said to be true breeding when all its progeny formed after self-pollination are tall.
Production of F1 plants: F1 generation is the first filial generation. It is formed after crossing the desirable parents. For example, Mendel crossed a pure tall pea plant with a pure dwarf pea plant. All F1 plants were found to be tall.
Results of self-pollination of F1 plants: Mendel found that on self-pollination of F1 plants, the progenies obtained in F2 generations were not all tall plants. Instead, one-fourth of F2 plants were found to be short.
Mendel’s explanation for the reappearance of the short trait:
From this experiment, Mendel concluded that F1 tall plants were not true breeding. They were carrying both short and tall height traits. They appeared tall, because tall trait was dominant over short trait.
Dominant trait: It is a trait or characteristic, which is able to express itself over another contrasting trait. For example, tall plants are dominant over short plants.
Recessive trait: It is a trait which is unable to express its effect in the presence of the dominant trait.
Mendel represented the dominant trait as upper case T (i.e. T for tallness), and the recessive trait as lower case t (i.e. t for shortness). These traits are actually the genes present in the chromosomes of a cell.
Thus, Mendel’s experiment can be represented as follows:

Revival of the trait that was unexpressed in F1 (dwarf) was observed in some F2 progeny. Both traits, tall and dwarf, were expressed in F2 generation in ratio 3:1.
Mendel proposed that something is being passed unchanged from generation to generation. He called these things as ‘factors’ (presently called genes). Factors contain and carry hereditary information. Traits may not show up in an individual but are passed on to the next generation.
Inheritance of traits over two generations
The appearance of F1 plants was similar to their parents i.e. they were tall, but were actually different from their parents. Mendel introduced the terms genotype and phenotype.
Genotype is the genetic constitution of an organism, which includes all genes that are inherited from both the parents. For example TT, Tt, and tt are genotypes of organisms with reference to their height.
Phenotype is the observable trait or characteristic of an organism, which is the result of genotype. For example, tallness and shortness are phenotypes resulting from different genotypes.
The above experiment of Mendel involved only one pair of contrasting characters (tall/short plant height), so it is called a monohybrid cross.
If two pairs of contrasting characters are involved, then the cross is termed as dihybrid cross
Inheritance of Two Genes (Dihybrid Cross)
• In dihybrid cross, we consider two characters. (e.g., seed colour and seed shape)
• Yellow colour and round shape is dominant over green colour and wrinkled shape.
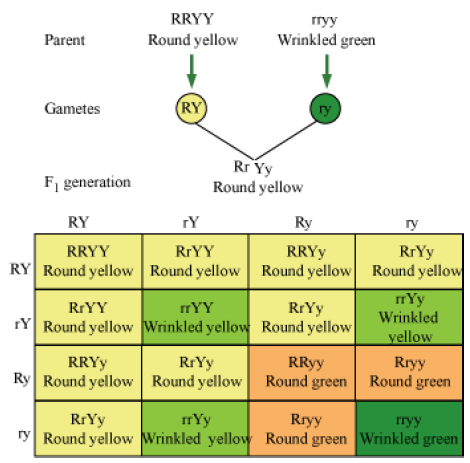
Phenotypic ratio − 9:3:3:1
Round yellow − 9
Round green − 3
Wrinkled yellow − 3
Wrinkled green −1
Mendel’s Laws of Inheritance
Principles of Mendel:
• Each characteristic in an organism is represented by two factors (it means that each cell has two chromosomes, carrying the gene for the same character).
• When two contrasting factors are present in an organism then one of them can mask the presence of the other. Therefore, one is called the dominant factor, while the other is called the recessive factor.
• When two contrasting factors are present in an individual, they do not blend and produce an intermediate type. However, they remain separate and get expressed in the F2 progeny. The plant with Tt genotype is tall and not of intermediate height.
• When more than two factors are involved, these are independently inherited.
Mendel’s Laws of Inheritance
Based on his experiments, Mendel proposed three laws or principles of inheritance-
• Law of Dominance
• Law of Segregation
• Law of Independent Assortment
Law of dominance and law of segregation are based on monohybrid cross while law of independent assortment is based on dihybrid cross.
Law of Dominance
• According to this law, characters are controlled by discrete units called factors, which occur in pairs with one member of the pair dominating over the other in a dissimilar pair.
• This law explains expression of only one of the parental character in F1 generation and expression of both in F2 generation.
Law of Segregation
• This law states that the two alleles of a pair segregate or separate during gamete formation in such a way that a gamete receives only one of the two factors.
• In homozygous parents, all gametes produced are similar; while in heterozygous parents, two kinds of gametes are produced in equal proportions.
Law of independent Assortment
• When two pairs of traits are combined in a hybrid, one pair of character segregates independent of the other pair of character.
• In a dihybrid cross between two plants having round yellow (RRYY) and wrinkled green seeds (rryy), four types of gametes (RY, Ry, rY, ry) are produced. Each of these segregate independent of each other, each having a frequency of 25% of the total gametes produced.
Sex Determination
• Henking discovered the genetic/chromosomal basis of sex determination by working on insects. He observed specific nuclear structures during spermatogenesis in insects. He named these structures as X bodies.
• He observed that after spermatogenesis, 50% of the sperm obtained these structures, while 50% did not.
• Later on, it was found that the X body observed by Henking was actually a chromosome and thus, this chromosome was named X chromosome.
• Chromosomes involved in sex determination are called sex chromosomes, while the other chromosomes are called autosomes. • XO type of sex determination
• Other than autosomes, at least one X chromosome is present in all insects.
• Some sperms contain X chromosomes, while some do not.
• Eggs fertilised by sperms having X chromosomes become females. So, females have two X chromosomes.
• Eggs fertilised by sperms not having X chromosomes become males. So, males have only one X chromosome.
• Example of organisms with XO type of sex determination − Insects
• XY type of sex determination
• Males have X chromosome and its counterpart Y chromosome, which is distinctly smaller. Hence, males are XY.
• Females have a pair of X chromosomes. Hence, females are XX.
• Example of organisms with XY type of sex determination − Humans and Drosophila
• Male heterogamety − XO and XY types of sex determination are examples of male heterogamety.
• In XO type, some gametes have X chromosomes, while some gametes are without X chromosomes.
• In XY type, some gametes have X chromosomes, while some gametes have Y chromosomes.
• Female heterogamety − ZW type of sex determination is an example of female heterogamety.
• In ZW type, the female has one Z and one W chromosome, while the male has a pair of Z chromosomes.
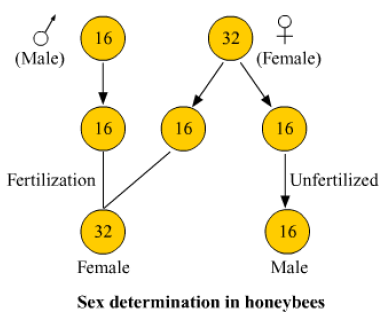
Sex Determination in honeybees –
• Honey bees show a special mechanism of sex determination called the haplo-diploidy.
• In honeybees, the sex of the offspring is determined by the fertilization or non-fertilization of eggs, rather than the presence or absence of sex chromosomes.
• The unfertilized honey bee eggs normally develop into male progeny and are haploid in nature (have just one set of chromosomes).
• The fertilized honey bee eggs, differentiate into queens and worker bees and are diploid in nature (have two sets of chromosomes).
What is Sex Linked Inheritance?
Genes carried by sex chromosome are said to be sex linked. The appearence of a trait because of the presence of an allele either on X chromosome or Y chromosome is called Sex-linked Inheritance.
Diseases observed in X-linked Inheritance
Any disease that is determined by the sex chromosomes, or that occurs due to defects in a gene on the sex chromosomes, is said to be sex linked. These diseases can descend to the offsprings from the parents through gametes. The diseases that occur due to any defective gene present on X chromosomes are known as X-linked diseases.
Most of these diseases are recessive in nature, that means, in the case of females, the defective allele should be present on both of the X chromosomes.
These disorders are more commonly observed in males as they have only a single X chromosome. A single recessive gene on that X chromosome will cause the disease. Most commonly observed diseases are:
• Haemophilia – It is a genetic disorder under which the sufferer (recessive X bearing male and homozygous recessive female) is at a risk of excessive blood loss leading to death as blood fails to clot.
• Colour blindness – It is also a genetic disorder in which the sufferer is unable to identify or distinguish between various colours. The following example will explain the sex-linked inheritance of colour-blindness in humans more clearly.


Criss-Cross Inheritance
The transfer of a gene from mother to son or father to daughter is known as criss-cross inheritance. For example, as in X-chromosome linkage.