Sample Paper ICSE Class 10 Mathematics Set B

Students can refer to the following Sample Paper ICSE Class 10 Mathematics Set B with Answers provided below based on the latest syllabus and examination guidelines issued for ICSE Mathematics. All specimen papers have been prepared covering all chapters given in ICSE Mathematics book for Class 10. You should also refer to ICSE Class 10 Mathematics Solutions.

Sample Paper ICSE Class 10 Mathematics Set B with Answers

MATHEMATICS
SECTION A (40 MARKS)
(ATTEMPT ALL QUESTIONS IN THIS SECTION)

QUESTION 1
a. Find the equation of the line passing through the points (0, -2) and the point of intersection of the lines 4x+3y=1 and 3x-y+9=0. [3]
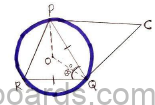
b. In the given figure PQ=RQ, <RQP=680, PC and QC are tangents to the circle with centre O. Calculate the values of <QOP and <QCP.

c. If (x-2) is a factor of the expression, 2𝑥³+𝑎𝑥²+b𝑥-14 and the expression is divided by (x-3), it leaves a remainder 52. Find the values of a and b.

QUESTION 2
a. The sum of the first 5 terms and the sum of the first 7 terms of the same AP is 167. If the sum of the first 10 terms of this AP is 235, find the sum of its first 20 terms. [3]
b. Prove that

QUESTION 3
a. If b is the mean proportion between a and c then, show that

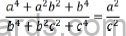
b. A tree breaks due to a storm and the broken part bends (without being detached) so that the top of the tree touches the ground making an angle of 30⁰ with it. The distance between the foot of the tree to the point where the top touches the ground is 8m. Find the height of the tree. [3]

c. Solve the linear inequation -2{5/6} < 1/2 – 2𝑥/3 ≤2, x Ꞓ N and graph the solution on the number line.

QUESTION 4
a. Find the values of m such that (3m+1)𝑥²+2(m+1)𝑥 + m=0 has real and equal roots. [3]
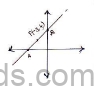
b. In the figure the line segment AB meets the x-axis at A and y-axis B. The point P (-3,4) on AB divides it in the ratio 2:3. Find the coordinates of A and B.

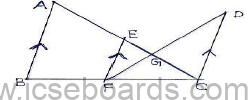
c. In the given figure AB II EF II CD, AB=7.5cm, EG=2.5cm, GC=5cm and DC=9cm. Calculate
(i)EF
(ii)AC.

SECTION B (40 MARKS)
(ATTEMPT ANY 4 QUESTIONS FROM THIS SECTION)

QUESTION 5
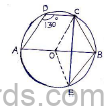
a. In the figure, AB is the diameter of the circle with centre O. If <ADC=1300 and chord BC = chord BE. Find <CBE.

b. The sum of four consecutive numbers in an AP is 32 and the ratio of product of the first and last term to the product of middle terms is 7:15. Find the numbers. [3]

c. From the top of a building AB, 60m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30⁰ and 60⁰ respectively. Find the horizontal distance BD and also the height of the lamp post.

QUESTION 6
a. Solve the quadratic equation 𝑥²+7 𝑥 = 7 and give your answer correct to 2 decimal places. [3]
b. Solve the inequation −𝑥/3≤ 𝑥/2 − 1{1/3}< 1/6, x ∈𝑅 and write the solution set. [3]
c. Given (x +1) and (x- 2) are factors of 𝑥³+a𝑥²– b x- 6. Find the values of a and b. With the values of a and b factorize the expression completely.

QUESTION 7
a. In an auditorium, seats were arranged in rows and columns. The number of rows was equal to the number of seats in each row. When the number of rows was doubled and the number of seats in each row was reduced by 10, the total number of seats increased by 300.
Find i) The number of rows in the original arrangement
ii) The number of seats in the auditorium after the rearrangement

b. If 𝑥=√𝑎+1 + √𝑎−1/√𝑎+1 − √𝑎−1 , using properties of proportion show that 𝑥²-2a 𝑥 +1=0. [3]
c. Find AB+2C-4D , given that

QUESTION 8
a. The midpoint of the line segment joining (4a,2b-3) and (-4,3b) is (2, -2a).
Find a and b. [3]
b. A and B are two points on the x-axis and y-axis respectively. P (2, -3) is the midpoint of AB. Find i) the coordinates of A and B
ii) the slope of AB
iii) the equation of line AB [3]
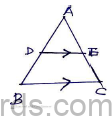
c. From the given figure i) prove that △𝐴𝐷𝐸 ∼△𝐴𝐵𝐶
ii) given that AD = ½ BD, calculate DE, if BC=4.5cm
iii) find 𝑎𝑟(△𝐴𝐷𝐸)/𝑎𝑟(△𝐴𝐵𝐶) and 𝑎𝑟(△𝐴𝐷𝐸)/𝑎𝑟(𝑡𝑟𝑎𝑝𝑒𝑧𝑖𝑢𝑚 𝐵𝐶𝐸𝐷).

QUESTION 9
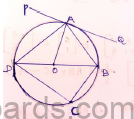
a) In the given figure <DAE = 70⁰. Find <BCD, <BOD, <OBD (give suitable reasons)

b) Prove that √𝑠𝑒𝑐²𝜃 +𝑐𝑜𝑠𝑒𝑐²𝜃= 𝑡𝑎𝑛𝜃 + 𝑐𝑜𝑡𝜃 [3]
c) Using properties of proportion solve for x, 2𝑥 + √4𝑥²−1/2𝑥 − √4𝑥²−1= 4, given that x is positive

QUESTION 10
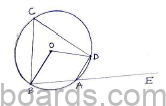
a. PQ is a tangent to the circle at A, DB is the diameter and O is the centre. If <ADB = 30⁰ and <CBD = 60⁰ calculate <QAB, <PAD, <CDB.

b. Find k such that the equation x²+4kx+(k²-k+2) = 0 has equal and real roots. [3]
c. A(2,5), B(-1,2) and C(5,8) are the vertices of a triangle ABC, M is a point on AB such that AM:MB=1:2. Find the coordinates of M. Hence find the equation of line passing through the point C and M.

QUESTION 11
a. For the AP: 10,15,20, …., 195, find
(i)the number of terms (ii)sum of all terms. [3]
b. Factorize 2𝑥³+3𝑥²−9𝑥−10 completely. [3]
c. Prove that 𝑐𝑜𝑠𝐴/1−𝑡𝑎𝑛𝐴+𝑠𝑖𝑛𝐴/1−𝑐𝑜𝑡𝐴= 𝑐𝑜𝑠𝐴 + 𝑠𝑖𝑛𝐴