Students can refer to the following Sample Paper ICSE Class 10 Mathematics Set D with Answers provided below based on the latest syllabus and examination guidelines issued for ICSE Mathematics. All specimen papers have been prepared covering all chapters given in ICSE Mathematics book for Class 10. You should also refer to ICSE Class 10 Mathematics Solutions.
Sample Paper ICSE Class 10 Mathematics Set D with Answers
MATHEMATICS
Std : 10 Max. Marks : 80
No. of Questions : 11
Duration : 2 ½ hours No. of Printed sides : 07
[Answers to this paper must be written on the paper provided separately.] You will not be allowed to
write during the first 15 minutes. This time is to be spent in reading the question paper.
Answer all questions from Section A and any four questions from Section B.
All working including rough work, must be clearly shown and must be done on the same sheet as the rest
of the answer. Omission of essential working will result in loss of marks. The intended marks for
questions or parts of questions are given in brackets [ ]. Mathematical tables and squared sheets
are provided.
Sample Paper ICSE Class 10 Mathematics Set D
SECTION A (40 Marks)
Answer all questions from this Section
Question 1
(a) If A =

(i) Write the order of matrix X
(ii) Find matrix X
(b) Mr. Davis has a cumulative deposit account in HDFC Bank for two years at 6% p.a. simple interest. If he gets 1200 as interest at the time of maturity, find: [3]
(i) the monthly instalment (ii) the matured value
(c) There are two dice; one red and the other black. Both are rolled simultaneously. Find the probability that: [4]
(i) the number on the red dice is either 3 or 5
(ii) the number on the black dice is 4
(iii) each dice shows five
(iv) the product of the numbers appearing on the top of the dice is less than 9
Question 2
(a) A cylinder having height and diameter 14 cm, is filled with water up to the brim. Four equal solid spheres are placed into it. The diameter of each sphere is equal to the radius of the base of the cylinder. What fraction of water overflows? [3]
(b) Mr Lai took a loan of 80,000 to buy a motor bike. He repays his total loan by paying every month starting with the first instalment of 1000. If he increases his instalment by 100 every month, what amount will be paid by him in the 24th instalment? What amount of loan does he still have to pay after the 24th instalment?
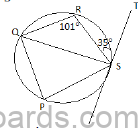
(c) P, Q, R and S are points on the circumference of the given circle TS is the tangent to the circle at the point S.
∠RST = 350,∠QRS = 1010
Find the magnitude of
(i) ∠QPS
(ii) ∠SQR
(iii) ∠ QPR
Question 3
(a) Using factor theorem factorise the following polynomials: [3]
x3 + 10x2 – 37x + 26
(b) Prove the following identity:
( 1 + cotθ – cosecθ ) ( 1 + tanθ + secθ ) = 2 [3]
(c) Write down the correct alternative in each of the following: [4]
(i) The median of the first 10 prime numbers is (a) 11 (b) 12 (c) 13 (d) 14
(ii) If the mean of 6, 7, x, 8, y, 14 is 9, then
(a) x + y = 21 (b) x – y = 19 (c) x + y = 19 (d) x – y = 21
(iii) For the following distribution –

the modal class is
(a) 10 – 20 (b) 20 – 30 (c) 30 – 40 (d) 50 – 60
(iv) If 35 is removed from the data: 30, 34, 35, 36, 37, 38, 39, 40, then the median increases by
(a) 2 (b) 1.5 (c) 1 (d) 0.5
Question 4
(a) Solve the following inequation, write down the solution set and represent it on the real number line. [3]

(b) The first term of a G.P. is 1. The sum of the third and fifth terms is 90. Find the common ratio and write down the GP. [3]
(c) Use graph paper for this question. [4]
Plot P( 2, 4 ) Q( -2, 1 ) and R( 5, 0 ) using scale 2 cm = 1 unit on both axes.
(i) Reflect P and Q in y = O to get P’ and Q’ and write their coordinates.
(ii) Give a geometrical name to the figure PQQ’P’R.
(iii) Find the area of the figure.
(iv) Write down the equation of QQ’.
SECTION B
(Answer only four)
Question 5
(a) If -4 is a root of the quadratic equation x2 + px – 4 = 0, find the value of p. Given that the quadratic equation x2 + px + k = 0 has equal roots, find the value of k.
(b) Use graph paper for this question. Take scale 1 cm = 1 unit on both axes. Plot A( 3, -2 ) B( 2, 1 ) and C( 10, 3 ). [3]
(i) Construct the locus of points at a distance of 5 cm from A.
(ii) Construct locus of points equidistant from B and C.
(iii) Locate point P such that PB = PC and P is at a distance of 5 cm from A. Write down the coordinates of P.
(c) Mr. Prasad invests 9,600 in 5% 100 shares at a discount of 20. After a year he sold these shares at 90 each and invests the proceeds (including his dividend) in 9% 50 shares at 57. Calculate: [4]
(i) his dividend for the first year.
(ii) his annual income in the second year.
(iii) the percentage increase in his return on his original investment.
Question 6

(b) Find the number of two digit numbers greater than 50, which when divided by 7 leaves a remainder 4. Also find their sum.
(c) Given P(1, 2) and S(-3, 0). P divides OQ in the ratio 2 : 3 and OPRS is a parallelogram. Find: [4]
(i) the coordinates of Q
(ii) the coordinates of R
(iii) the equation of a line through P parallel to the y-axis

Question 7
(a) Solve the quadratic equation 3×2 – x – 7 = 0 and give your answer correct to 3 significant figures. [3]
(b) From the given graph (i) Prove Δ AOB ∼ Δ COD

(c) Prove the following identity:
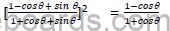
Question 8
(a) If y is the mean proportion between x and z, show that

(b) Draw a line segment AB of length 8 cm. Taking A as centre draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm.
Construct tangents AX and AY to the circle with B as centre and construct tangents BM and BN to the circle with A as centre. Measure and record the lengths of each tangent. [3]
(c) Ayan has a cumulative deposit amount of 340 per month at 6% per annum. If he gets 7157 at the time of maturity, find the total time for which the account was held.
Question 9

Evaluate B x A without using log tables.
(b) Ratanpura village is situated 3 km away from Dhule district in Maharashtra State. Google maps on which they are shown is drawn to a scale of 1 : 5000. [3]
(i) Calculate the distance between the two villages in cm on the map.
(ii) On the map a rectangular paddy field has an area of 5 cm2. Calculate the actual area of the paddy field in square metres.
(c) The following table gives the pocket money of 200 students in Std 10. [4]
Calculate the mean of the following distribution by step – deviation method.

Calculate the new mean if the pocket money increases by 21.50.
Question 10
(a) A circle is inscribed in ΔABC, AB = 7 cm, BC = 8 cm, AC = 5 cm. If P is the point of contact of the circle with side BC, find the length of BP.
(b) An electrician has to repair an electric fault on an electric pole of height 10m. He needs to reach a point 3.1m below the top of the pole in order to undertake the repair work. What should be the length of the ladder that he should use which when inclined at an angle of 600 to the horizontal, would enable him to reach the required position? Give your answer correct to the nearest metre. Take √3 = 1.73
(c) In the figure given below, diameter AB and chord CD of circle with centre O intersect at P. PT is the tangent to the circle at T. CD = 15 cm, DP = 12 cm, BP = 6 cm, find: [4]
(i) the radius of the circle.
(ii) the length of the tangent PT.

Question 11
(a) A cone of radius 9cm and height 12 cm is full of water. A sphere which exactly fits and touches the sides of the cone is immersed in it. Find: [4]
(i) the radius of the sphere.
(ii) the fraction of the water that overflows

(b) Use a graph sheet to answer this question.
The following table gives the record of weight in kilograms of students residing in a boarding house. Taking scale 2cm = 20 students on one axis and 2cm = 5kg on the other axis, draw an ogive for the given distribution

Use your ogive to estimate the following:
(i) The median weight.
(ii) The percentage of students weighing 55kg or more.
(iii) The number of students who are overweight if 57.5 kg is considered as the standard weight.
(iv) The weight above which the heaviest 30% of the students fall.