Students can refer to the following Sample Paper ICSE Class 10 Mathematics Set F with Answers provided below based on the latest syllabus and examination guidelines issued for ICSE Mathematics. All specimen papers have been prepared covering all chapters given in ICSE Mathematics book for Class 10. You should also refer to ICSE Class 10 Mathematics Solutions.
Sample Paper ICSE Class 10 Mathematics Set F with Answers
Grade: X
Subject : Mathematics
• You will not be allowed to write during the first 15 minutes.
• This time is to be spent in reading the question paper.
• The time given at the head of this paper is the time allowed for writing the answers.
• This paper consists of 5 printed pages.
• Attempt all questions from Section A and any four questions from Section B.
• All working including rough work should be clearly shown and must be done on the same sheet as the rest of the answer.
• Omission of essential working will result in loss of marks.
• All figures in geometry have to be copied on the answer sheet.
• The intended marks for questions or parts of questions are given in brackets [ ].
Section A
Attempt all questions from this Section
Question I

(b) There were 50 questions in an examination paper numbered 1 to 50. Write down the probability that the number of question chosen will: [3]
(i) contain more than one digit.
(ii) contain at least one figure 4.
(iii) end in 4.
(c) Find the values of a and b if (x – 1) is a factor of ax3 – x2 – bx + 6 and when this polynomial is divided by (x – 3), remainder is 30.
Question 2
(a) Mr. Rathod opened a recurring deposit account in a bank paying 12% p.a. At the end of 2 years he received 6750. Calculate his monthly instalment. [3]
(b) Solve and give answer correct to 3 significant figures. X-18/x= 6 [3]
(c) If the 3th and 7th term of a GP are 2 and 512 respectively, find: [4]
(i) the first term
(ii) the sum of its first 5 terms.
Question 3
(a) Solve the following linear inequation and represent the solution set on the number line:

(b) In the adjoining figure, D is a point on BC such that ∠ABD = ∠CAD, If AB = 5 cm, AC = 3 cm and AD = 4 cm, find:
(i) BC
(ii) area of ∠ACD : area of ∠BCA

(c) The surface area of a solid metallic sphere is 5024 cm2. It is melted and recast into solid cones of radius 5 cm and height 10 cm. Calculate: (π = 3.14) [4]
(i) the radius of the sphere
(ii) the number of cones recast.
Question 4
(a) Prove the identity

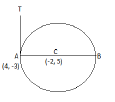
(b) AB is a diameter of a circle with centre C (-2, 5). If A is (4, -3) find: [3]
(i) the coordinates of B.
(ii) equation of tangent AT.
(c) In the given figure, I is the incentre of AABC. BI when produced meets the circumcircle of Δ ABC at D.

Given ∠BAC = 550 and ∠ACD = 650, calculate:
(i) ∠DCA (ii) ∠DAC
(iii) ∠DCI (iv) ∠AIC
Section B
Attempt any four questions from this Section
Question 5
(a) If x = 4 is one root of (k + 2) x2 – (5k + 2)x – 4 = 0, find the value of k. Also, find the other root of the equation. [3]
(b) Ashish buys 70 shares available at 125 (par value 100). [3]
(i) How much is his investment?
(ii) If the dividend is 7.5%, what will be his annual income?
(iii) If he wants to increase his income by 105, how many extra shares should he buy?
(c) Plot P(2, 4), Q (-2, 1) and R (5, 0). Reflect points P and Q in x –axis to get P’ and Q’. [4]
(i) Write their co-ordinates.
(ii) Give geometrical name to the figure formed by joining the points PQQ’P’R.
(iii) Find the area of figure PQQ’P’R.
Question 6
(a) Using properties of proportion, solve for x :

(b) Find the mean of the following by step-deviation method

(c) Construct a regular hexagon of side 5 cm. Locate a point O inside the hexagon which is equidistant from its all sides. Construct a circle circumscribing the hexagon. All traces of construction must be clearly shown.
(a) The digits of a 3 digit positive number are in AP and their sum is 15. The number obtained by reversing its digit is 792 more than the original number. Find the original number. [3]
(b) Using factor theorem, factorise the following polynomial: [3]
X3 + 10x2 – 37x + 26
(c) Find the mode of the following distribution by drawing histogram.

Question 8
(a) If 16 is the mean proportional between two numbers a and b and 128 is the third proportional to a and b, find the numbers. [3]
(b) A toy model of a truck and a real truck are in the ration 1:60. [3]
(i) If the length of the model is 25 cm, calculate the length of the truck, in meters.
(ii) If the open area of loading of the truck is 90 m2, find the same area of the model in cm2.
(iii) The volume of the model is 7500 cm3, find the volume of the truck in m3.
(c) Some glass flower vases were bought for 6000. Ten were damaged during transportation. The remaining were sold for a total profit of 1200 by selling each for 60 more than what was paid for. Find the number of vases bought
Question 9
(a) A boy is flying a kite with a string of length 80 m. The angle of elevation of the kite is found to be 300. On the other side of the kite, a girl standing near the window at a height of 16 m observes ∠ of elevation of kite of 600. Find the distance between the girl and the kite.
(b) Use graph paper for this question.

Using a scale of 2 cm = 1000 on one axis and 2 cm = 20 employees on another draw the ogive and from it determine: [6]
(i) the median income
(ii) the lower quartile
(iii) the number of employees getting above 15500.
(iv) the number of employees getting below 9500
Question 10
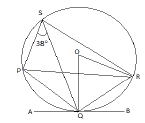
(a) AB id a tangent to the circle at Q. [3]
PQRS is a cyclic quadrilateral.
If ∠PSQ = 380, ∠PQR = 1100
find:
(i) ∠QPR (ii) ∠PQA

(c) A test tube consists of a hemisphere and a cylinder [4]
of the same Radius. Volume of water required to fill the tube is 2849/8 cm3 And 2618/3 cm3 of water to fill the tube to a level 2 cm below the top. Find the radius of the tube and the length of cylindrical part.

Question 11
(a) Provide the identity
(b) Construct a cyclic quadrilateral ABCD in which AB = 5 cm, BC = 8 cm, ∠ABC = 600 and D is equidistant from B and C. [3]
(c) A man wants to repay 81,880 in 11 monthly instalments, such that each instalment is double the value of the earlier. Find the values of the first and the last instalments.