Students should refer to Current Electricity ICSE Class 10 Physics Notes and solutions below. Our teachers have provided numerical problems and solutions for chapter Current Electricity in ICSE Class 10 Physics. These notes are really useful if you are preparing for ICSE exams. concise physics class 10 solutions are also very important for Physics students.
ICSE Class 10 Physics Current Electricity Numerical Problems
Students can refer to the Numerical Problems prepared for Chapter Current Electricity in Class 10 ICSE. These notes will be really helpful for the students giving the Physics exam in ICSE Class 10. Our teachers have prepared these concept notes based on the latest ICSE syllabus and ICSE books issued for the current academic year. Please refer to Chapter wise notes for ICSE Class 10 Physics provided on our website.
Current Electricity ICSE Class 10 Physics Revision Notes
Revision Notes
➢ A sustained electric current flows through a conductor only when it is connected to a source of emf.
➢The electric current, in a given conductor is simply the rate of flow of charge across its cross section. Thus,
I = Q/t
➢The unit of current is ampere (A). We have
1 A = 1 coulomb per second = 1 Cs-1
➢The current, flowing through a wire, is said to be one ampere when one coulomb of charge flows across its cross-section in one second.
➢Potential is the electrical state of a conductor which determines the direction of flow of charge when two conductors are either kept in contact or joined by a metallic wire. The potential at a point is defined as the amount of work done in bringing a unit positive charge from infinity to that point. The potential difference (p.d.) between two points is simply the work done in transporting a positive charge of one coulomb from the first point to the second point. W = QV
➢The unit of potential difference is volt (V). We have 1 volt = 1 V = 1 joule per coulomb = 1 JC-1. The potential difference between two points equals one volt if the work done in transporting a charge of one coulomb between these points equals one joule.
➢Electromotive Force : When no current is drawn from a cell, then the potential difference between the terminals of the cell is called electromotive force. It is denoted by e. Its unit is volt. The electromotive force of a cell depends upon (i) the material of the electrodes, (ii) the electrolyte used in the cells.
➢According to Ohm’s Law :
➢The current flowing through a given conductor is directly proportional to the potential difference across its ends, provided the physical conditions of the conductor (e.g., its length, its area of cross-section, its temperature, etc.) remain constant.
➢The resistance of a conductor equals the ratio of the potential difference across its ends to the current flowing through it. Thus, the resistance of the conductor is numerically equal to the potential difference across its ends when unit current flows through it.
R = V/I or V = IR or I = V/R
➢The obstruction offered to the flow of current by the conductor (or wire) is called its resistance. The unit of resistance
is ohm (Ω). A conductor has a resistance of one ohm when a potential difference of one volt across its ends causes a current of one ampere to flow through it.¾ ¾ The resistance associated with the electrolyte of a cell—within its electrodes—is known as the internal resistance of the cell.
➢When a cell of emf ε, and internal resistance r, is connected across an external resistance R, current flows through the circuit. I = ε/(R + r) and V = ‘p.d.’ across R = IR
➢The internal resistance of a cell depends on
(iv) the nature, concentration and temperature of its electrolyte.
(v) the surface area of the (‘dipped within the electrolyte’ part) electrodes.
(vi) the distance between the electrodes.
➢ An increase in the surface area of the electrodes causes the internal resistance to decrease, whereas an increase in the distance between the electrodes causes the internal resistance to increase. Internal resistance decreases with increasing temperature or concentration of an electrolyte.
➢Factors Affecting the Resistance of a Conductor
The electrical resistance of a conductor depends on the following factors :
(i) Length of the Conductor : The resistance of a conductor R is directly proportional to its length l
i.e., R ∝ l
∴ When the length of a wire is doubled or halved, then its resistance also gets doubled or halved respectively.
(ii) Area of Cross-Section of the Conductor : The resistance of a conductor R is inversely proportional to its area of cross-section A.
i.e., R ∝ 1/A
∴ When the area of cross-section of wire is doubled, its resistance gets halved and if area of cross-section of wire is halved, its resistance will get doubled.
(iii) Nature of the Material of the Conductor : The resistance of a conductor depends on the nature of the material of which it is made of. Some materials have low resistance whereas others have high resistance.
(iv) Effects of Temperature :
(a) Resistance of a conductor increases linearly with increase in temperature.
(b) Resistance of a semiconductor decreases with increase in temperature.
(c) Resistance of insulators (non-conductor) decreases with increase in temperature.
(d) Resistance of electrolytes decreases with increase in temperature.
From the above relation (i) and (ii), we can write R ∝ 1/A or R =ρ 1/A where, ρ is the constant of proportionality called resistivity or specific resistance of the conductor.
➢Ohmic and Non-Ohmic Resistor :
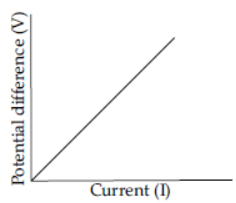
The conductor which obeys Ohm’s law is called ohmic resistor (or linear resistance), e.g., Silver, nichrome, copper,
iron etc. The graph of V vs I a straight line. The conductor which does not obey Ohm’s law is known as non-ohmic
resistor for non-linear resistance) e.g., Triode valve, junction diode, transistor, etc. The graph of V vs I a curved line.
➢ Superconductor : It is a substance of zero resistance at a very low temperature. e.g., Mercury, niobium, etc.
➢ Resistivity of a material is the resistance of a wire of that material of a unit length and unit area of cross section.
➢ Difference between ohmic and non-ohmic resistor :

➢ Difference between Resistance and Resistivity :

➢ The e.m.f of a cell is defined as the energy spent (or the work done) per unit charge in taking a positive charge around the complete circuit of the cell (i.e., in the circuit outside the cell as well as in the electrolyte inside the cell).
➢ When no current is drawn from a cell i.e., when the cell is in open circuit, the potential difference between the terminals of the cell is called its electro-motive force or (e.m.f.).
➢ When current is drawn from a cell i.e., when the cell is in a closed circuit, the potential difference between the electrodes of the cell is known as its terminal voltage.
➢ The terminal voltage of a cell is defined as the work done per unit charge in carrying a positive charge around the circuit across the terminals of the cells.
➢Difference between E.M.F. and the terminal voltage of cells :

➢ When the resistance of the combination is to be increased, they are combined in series and when the resistance of the combination is to be decreased, in order to pass a heavy current in the circuit, they are combined in parallel.
➢ V-I graph :
The below graph gives the graphical representation of Ohm’s law where the slope of V-I graph gives the resistance of the conductor.
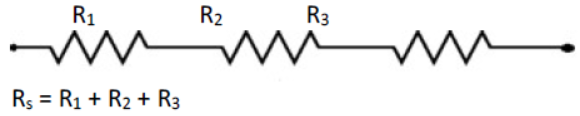
➢ Combination of resistors in Series :
Three resistors R1, R2 and R3 are connected in series. The same current I, flows through all the three resistors but the potential across each resistor is different and let it be V1, V2 and V3 .
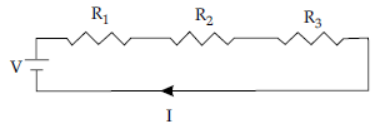
V = V1 + V2 + V3
= IR1 + IR2 + IR3( Using Ohm’s law, V = IR )
IReq = I (R1 + R2 + R3)
Req = R1 + R2 + R3
So, the equivalent resistance in a series combination is the sum of all resistances.
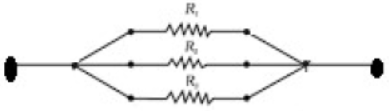
➢ Combination of resistors in Parallel :
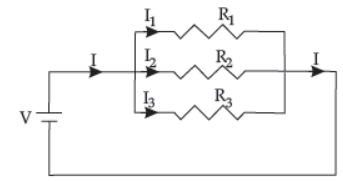
Three resistors R1, R2 and R3 are connected in parallel. The same potential difference, V exist through all the three resistors but the current across each resistor is different and let it be I1, I2 and I3 .
Net current, I = I1 + I2 + I3
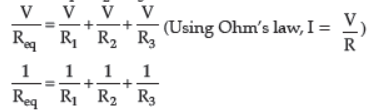
So, the reciprocal of equivalent resistance in a parallel combination is equal to the sum of reciprocal of individual resistances.
➢ Combination of resistors in Parallel :
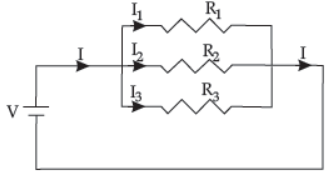
Three resistors R1, R2 and R3 are connected in parallel. The same potential difference, V exist through all the three resistors but the current across each resistor is different and let it be I1, I2 and I3 .
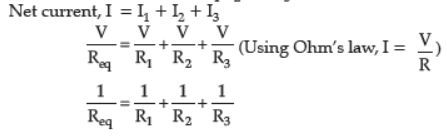
So, the reciprocal of equivalent resistance in a parallel combination is equal to the sum of reciprocal of individual resistances.
➢ The following two facts are to be noted about the series combination.
(i) The current has a single path for its flow. Hence, the same current passes through each resistor, so the potential difference across any resistor is directly proportional to its resistance.
(ii) The potential difference across the entire circuit is equal to the sum of potential differences across the individual resistor, i.e.,
V = V1 + V2 + V3 ….
➢ The following two points are to be noted about the parallel combination.
(i) The potential difference across each resistor is the same (V1 = V2 = V3 say) which is equal to the potential difference across the terminals of the battery (or source).
(ii) The main current I from the battery divides itself in different arms. The low resistance arm allows more current and the high resistance arm allows less current, i.e., the current in a resistor is inversely proportional to its resistance. The sum of currents I1 I2 I3 … in the separate branches of the parallel circuit is equal to the current I drawn from the source i.e., I = I1 + I2 + I3 + …
TOPIC-2
Electric Power and Energy, Fuse, Household Circuit
Revision Notes
➢ In India, electric power for domestic use is supplied with alternating current (a.c.) at a frequency of 50 Hz with a (rms) potential difference of 220 V between the phase (or live) wire and the neutral wire.
➢ The neutral and the earth wires of the local sub-station are usually connected together so that the neutral wire is at the same potential as the earth. The live or the phase wire is then at a potential of 220 V (rms) with respect to either the neutral or the earth wire.
➢ Connection of all appliances (bulb, fan, socket, etc.) with the mains :
We note that all the electrical appliances (say, bulbs, fans, sockets, etc) are connected in parallel at the mains, each with a separate switch and a separate fuse connected in the live wire.
➢ Advantages of connecting the appliances in parallel :
(i) Each appliance gets connected to 220 V supply (= its voltage rating) for its normal working.
(ii) Each appliance works independently without being affected by the status of the other appliance being switched on or off.
➢ Disadvantages of connecting the appliances in series :
(I) The voltage of source gets divided in all the appliances connected in series, in a ratio of their resistances, so each appliance does not operate at its rated voltage.
(ii) On connecting one more appliance in the same circuit, the resistance of the circuit will increase. Hence it will reduce the current in the circuit, so each appliance will get less power.
(iii) All appliances connected in series operate simultaneously. None of the appliances can be operated independently. If one appliance is switched off or not operated, no other appliance connected with it in series will then operate.
➢ Electrical energy is very important in our day-to-day life. This is because of the case with which it can be converted into other forms of energy.
➢ The flow of an electrical current through a conductor produces heat. The heating effect associated with a current is expressed by Joule’s Law, according to which
H = I2 Rt = V2 t/R = IVt.
➢ The electrical power of a given device is simply the rate at which electrical energy is being consumed by it.
➢ We have P = IV = I2R = V2/R
➢ The resistance R (in ohm) of a device of power P watt, working at an applied p.d. of V unit, is given by
R = V2/P ohm.
➢ One watt is the electric power consumed when a current of 1 ampere flows through a circuit having a potential difference of 1 volt.
➢ We need both conductors (materials which let electricity flow through them easily) and insulators (materials which do not (easily) let electric current flow through them) for safe and proper use of electrical energy.
➢ All electric circuits (closed conducting paths used for ensuring a flow of electric current) need by :
(i) A source of electricity (cell, battery, generator, ‘mains’, etc.)
(ii) Conducting wires or conductors for providing a path for the flow of current and
(iii) A switch or a key for switching ‘ON’ and ‘OFF’ electric energy as per our requirements.
➢ SI Units :

By the definition of potential difference, work needed to move a charge Q through a potential difference V is
W = QV
But Q = I × t
W = VIt
Using Ohm’s law, W = I2 Rt = (V2 /R) t
➢ The unit often used for estimating the consumption of electrical energy is the kilowatt hour (kWh). One kilowatt-hour (kWh) is the electrical energy consumed by an electrical appliance of power 1 kW when it is used for 1 hour.
1 kWh = 1000 W × 3600 s
= 3.6 × 106 J
➢ Electrical energy consumed by appliance (in kWh) = power (in kW) × time (in h)
= power (in watt) × time (in hour) × 103
= V (volt) × I (in ampere) × t (hour) × 103
➢ Cost of electricity = electrical energy in kWh × cost per kWh
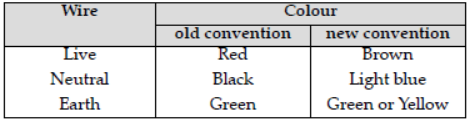
➢ Colour coding of wires in a cable :
➢ A fuse is a safety device which limits the flow of current in a circuit and thus protecting the device from being damaged.
➢ Fuse is made up of material having low melting point.
➢ A switch is an ON/OFF device which is connected in a circuit to the live wire.
➢ Earthing protects the appliance from getting damaged due to excessive current. If excess current flows, it passes through the earth wire to the earth. In local earthing, the earth connection at a meter is connected to a thick copper wire, which is buried deep in the earth and its ends are connected to a copper plate surrounded by a mixture of charcoal and salt. The thick copper wire is covered by a hollow pipe and water is poured into the pipe from time to time to provide a conducting layer between the plate and the ground.
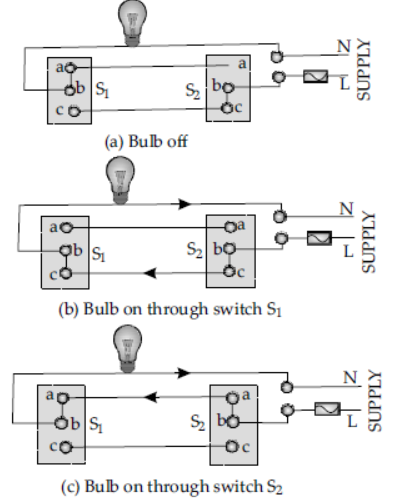
➢ Staircase wiring or dual control switch has two pathways for making the switch ON/OFF. The following diagrams illustrate a dual switch with two switches S1 and S2. The circuit can be switched on either using switch S1 or S2. When the connection ba is changed to bc, the circuit is completed and the switch operates by S1 whereas when the connection bc is changed to ab, the circuit is completed and the switch operates by S2.
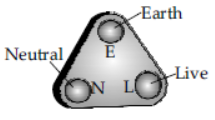
➢ Three pin plug has three pins – the top pin is for earth (E), the left pin is for live (L) and the right pin is for neutral (N).The earth pin is made longer and thicker so that firstly earth connection is made and if the device is faulty then after live connection is made, the current passes to the earth through earth wire.
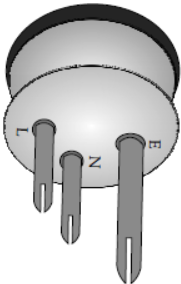
➢ A socket is fixed in the board of the circuit so that plug can be inserted. It has three holes which have a hollow metallic tube. The upper bigger hole is for earth connection, the left is for neutral and right for a live wire.
➢ Safety precautions while using electricity :
(i) Never touch the appliance with wet hands.
(ii) The wires carrying current should be having higher capacity than the total current which would flow when all the appliances are switched on.
(iii) Each appliance must be provided with a fuse.
(iv) The insulation of wires should be of good quality and that should be checked from time to time.
(v) Local earthing should be done near kWh meter.
IMPORTANT FORMULAS



If a cell of emf ɛ and internal resistance r sends a current I in an external resistance R, then
If a cell of emf ɛ and internal resistance r sends a current I in an external resistance R, then
• Total Resistance of the circuit = R+ r.
• Current dream from the cell 𝐼 = ε / R+r
• Terminal voltage of the cell 𝑉 = 𝑇𝑅 = ɛr / R+R
• Voltage drop inside the cell, 𝑉 = 𝐼𝑟 = ɛR / R+r
• E.m.f of the cell, ɛ = V+ v =IR+ Ir = I(R+ r)
• Internal resistance of a cell, 𝑟 = (ɛ/V -1)
POINTS TO REMEMBER
1) Current:
• S I unit of current is ampere (A)
• Bigger units are kilo ampere(kA=103A) & mega ampere [MV=106A]
• small units are milliamp ere(mA=103A) & Micro ampere (A=10-6A)
2) Potential difference:
• S.I unit of potential difference is volt(v).
• Bigger units are kilovolt(kV=103) and megavolt ( MV=106V)
3) Resistance:
• S.I unit of resistance is ohm(Ω).
• Bigger units are kilo-ohm(kΩ =103Ω) and mega ohm (MΩ = 106Ω) and
Giga Ohm (G Ω) = 109 Ohm.
4) Specific Resistance:
• S.I unit of specific resistance is ohm-meter (Ω-m)
• C.G.S unit of specific resistance is ohm-cm (Ω- cm)
5) Unit of electric charge: The unit of electric charge is coulomb one coulomb is equivalent to total change 6.25* 1018 Electrons.
6) The charge on one electrons is equivalent to 1.6*10-19C.
7) Potential difference: Potential difference between two points in an electric circuit is the amount of work done to move certain amount of change from one point to another point.
Potential difference (v) = Work done(w) / Amount of charge (Q)
Potential difference measured in volts.
One Volt is the potential difference, if one joule of work is done in moving a charge of one coulomb.
8) The current in series circuit is a constant quantity. There is a continuous drop in potential all along in series circuit, but potential difference goes on increasing. Total potential difference (p.d) in series circuit is equal to the sum total of p.d across the terminals of individual resistors.
i.e. V= V1+ V2+V3.
9) Parallel circuit: When a number of resistors are connected such that they have a common positive and a common negative terminal then resistors are said to be in parallel circuit.
The potential difference in a parallel circuit is a constant quantity
The current divides in parallel circuit in the inverse ratio of resistance
Total current flowing through parallel circuit is equal to the sum total of current flowing through individual resistors.
i.e. I=I1+I2+I3
10) Conductivity: The reciprocal of resistivity is called conductivity. It is abbreviated by the symbol σ, called Sigma.
SI Unit is Ohm-1M-1 or Siemen metre-1.
σ = 1/p = L/RA
11) Conductance The reciprocal of resistance is called conductance.
Conductance = 1/ Resistance
Its unit is mho or Siemen.
12) Q when do we join resistors in (a) series (b) parallel
(a) In order to increase the resistance of a circuit resistors are connected in series.
(b) When we have to decrease the resistance of a circuit in order to pass heavy current, resistors is connected in parallel.
𝑅𝑝 = 1/𝑅1 + 1/𝑅2 +1/𝑅3
(c) Special Cases : If two resistors are connected in parallel then
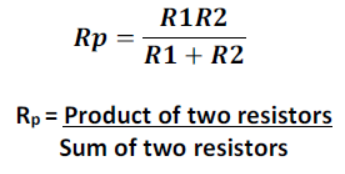
If I is the current drawn from the battery current I, flowing in resistor R, is given by
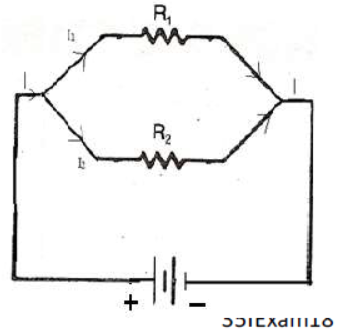

If ‘n’ identical resistors are connected in parallel, the equivalent resistor Rp is given by
13) Relation between resistivity and conductivity of a conductor:
Conductance X 1 /Resistivity
14) Relation between E.M.F; P.D; Internal Resistance and External Resistance:

- 2.Drop in potential at the terminal of cell is the product of current drawn from the cell and internal resistance of cell.
E-V = Ir - 3.If a large current is drawn from cell i.e. external resistance is low then drop in potential is very large.
(E.M.F – E, P.D- v, internal resistance-r & external Resistance →R)
15) Cells in series can give a large current only if their internal resistance is so small that it can be neglected is negligible with respect to external resistance.
Current in external circuit= Total E.m.f
Total resistance of circuit ⇒ 𝐼 =nE /R+nr
If ‘r’ is so small that it is negligible, them 𝐼 = 𝑛*e/R
It is for this reason that lead acid accumulators are connected in series.
16) Cell can give maximum current in parallel only if external resistance is very small and internal resistance is large.
𝐼 =𝑛*E/r
17) Melting point of tungsten is about 30000C.
18) The number of electrons contained in one coulomb of charge is 1.6 X 10-19.
19) Value of specific charge on an electron is 6.25* 10-18C.
20) The SI units for electric intensity are NC-1.
21) 1 KWh is equivalent to 3.6 X 106J.
IMPORTANT PROBLEMS AND SOLUTIONS
1) An experiment is performed to verify ohm’s law observations and tabulated and follows.

(i) From the data, plot a V-I graph
(ii) Show that the graph confirms the Ohm’s law
(iii) Find the resistance of the resistor used
(i) The required graph is Shown.
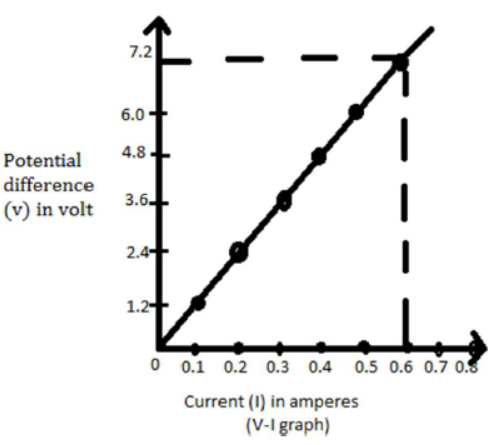
(ii) We observe that the graph drawn potential difference verses current is a straight line. This confirms the Ohm’s law.
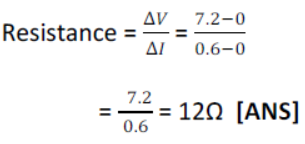
2) What should be the length of nichrome wire of resistance 5 Ω if the length of similar wire is 60 cm and resistance 2.5 Ω?
Ʀ1 = 5Ω , L2 = 60 cm, R2 = 2.5 Ω, L1 = ?
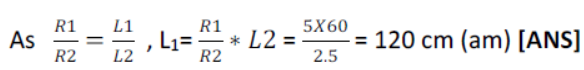
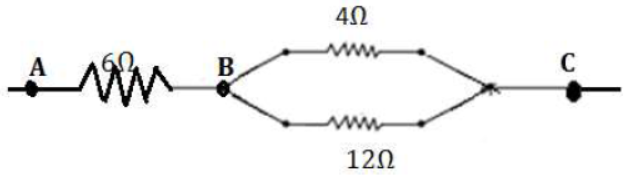
3) Calculate the equivalent resistance between point A and C, as show in figure.
Resistance of 4 Ω and 12 Ω are connected in parallel between point B and C let R1 be their equivalent resistance
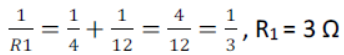
Now equivalent resistance R1 in series with 6 Ω resistance let R be the equivalent resistance of circuit.
Ʀ = 6+3 = 9 Ω [ANS]
4) An in candescent lamp of resistance 80 Ω draws a current of 0.75 A find the line voltage.
I = 0.75 A, R = 80 Ω V=? , by ohm’s law =V/R , V= IR = 0.75/80 = 60 Volts. [ANS]
5) Calculate the equivalent resistance of the following combination of resistors r1, r2, r3 and r4

The resistors r3 and r4 are in parallel if r is equivalent resistance of resistors r3 and r4 then
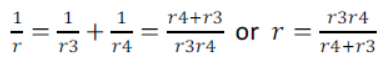
Now resistors r1, r2, and r3 are in series equivalent resistance
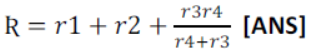
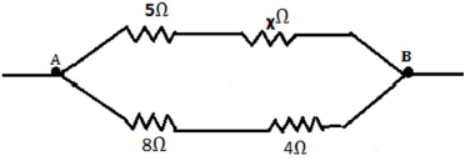
6) The equivalent resistance of the following circuit diagram is 4 Ω calculate the value of ‘X ’.
Resistance of 5 Ω and X Ω are in series.
Similarly, resistance of 8 Ω and 4 Ω are in series.
Equivalent resistance.
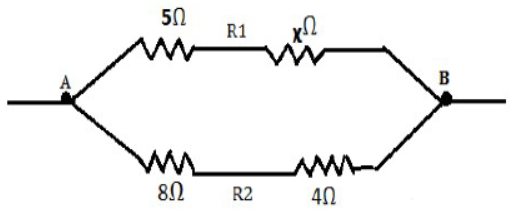
R1 = (5 +) Ω,
R2 = 8+4 = 12 Ω
Now R1 and R2 are in parallel combination
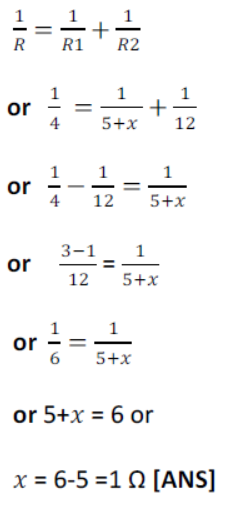
7) Calculate the resistance between the points X and Y in the given figure below.
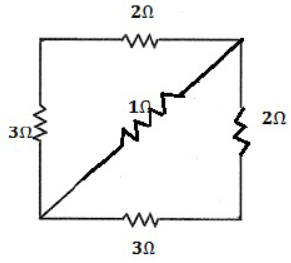
We can draw the given circuit as shown here
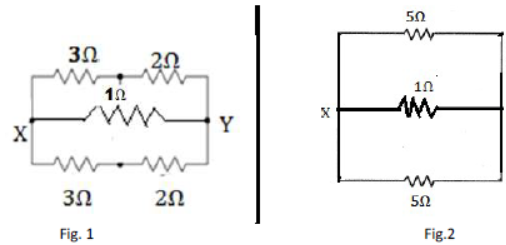
The resistors of 3 Ω and 2 Ω are in series
Their equivalent resistance = 3 Ω + 2 Ω = 5 Ω Now the resisters of 5 Ω, 1 Ω and 5 Ω are in parallel
as shown in alongside fig (ii)
Their equivalent resistance
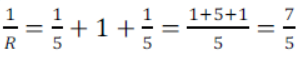
Or Ʀ = 71 Ω
Hence the resistance between X and Y is 0.71 Ω. [ANS]
8) Calculate the specific resistance of the material of a wire 1.1 m long 0.4 mm in diameter and having a total resistance of 4.2 ohm?
Specific resistance =? = 1.1m
Diameter = 0.4 mm,
r = 0.4/2
mm = 0.02 cm
R= 4.2 ohm
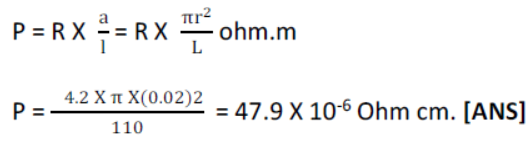
9) Two resistances of 2 ohm and 4 ohm are first connected to each other in series and then in parallel. Find the resistance of the combination in each case.
R1 = 2 ohm, r2 = 4 ohm, Rp =? , Rs =?
(i) In series Rs = r1 + r2
Rs= 2+4 =6 ohm
(ii) In parallel
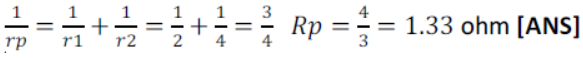
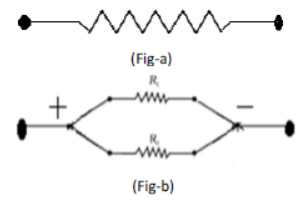
10) A wire of resistance ‘r’ ohm is doubled up by connecting its free ends together. What will be the resistance of wire in its new shape?
Let ‘r’ be the resistance of wire (fig-a) as its free ends are joined together, it becomes a combination of two wires each of resistance r/2 connected in parallel with each other (fig-b)
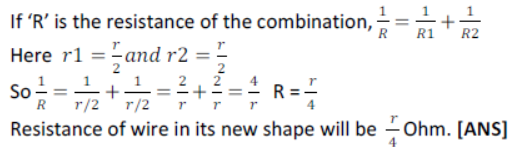
11) Calculate the number of electrons passing per second through a conductor to give a current of 1 amp. Charge on an electron = 1.6 X 10-19C.
Let ‘n’ be the number of electrons passing per second through the conductor when 1 ampere current passes , then Total change passing per second = ne
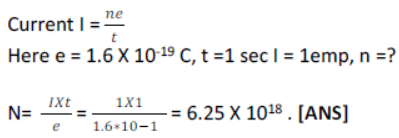
12) Given fig shows a circuit diagram having a battery of 24V and negligible internal resistance. Calculate the (a) reading of ammeter and (b) Readings of V1 , V2 and V3
E = 24 V
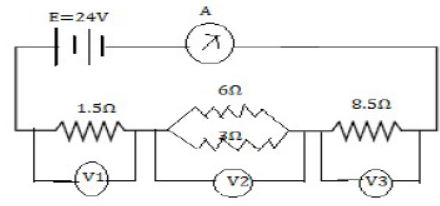
Resistance of 6 Ω and 3 Ω are in parallel. Their equivalent resistances,
1/R1 = 1/6 + 1/3 =1+2 /6 = 3/6 = 1/2 or R1 = 2Ω
Now resistances of 1.5 Ω, R1 and 8.5 Ω are in series
Total resistance = 1.5 + R1+ 8.5
= 10 + R1 = (10+2) Ω
= 12 Ω
(a) Current drawn from cell (ammeter reading)
I = V/R = 24/12 = 2 A Ans
(b) P. D. across 1.5 Ω resistor
V1= IR = 2 X 1.5 = 3V
P.D. across 2 Ω (Combination of 6 Ω and 3 Ω in parallel) resistor.
V2 = IR = 2 X 2 = 4V
P.D across 8.5 Ω resistor
V3 = IR = 2 X 8.5 = 17 V
Thus, the values of V1 , V2 and V3 are 3 V, 4 V and 17 V. [ANS]
13) Calculate the resistance of Eureka wire 110 cm long and 0.2mm in diameter. Given specific resistance of Eureka = 49= 10-8 ohm-m.
Here L= 110 cm = 1.10m,
r=0.1 mm= 10-4 m,
p= 49 X 10-8 ohm .m
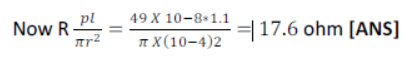
14) Four cells each of 1.5 volt e.m.f and 20 ohm internal resistance are used to send a current through a wire of 20 ohm resistances. The cells are arranged (i) all in series (ii) all in parallel. Calculate the current in the wire in each case
(i) Cells connected in series I =
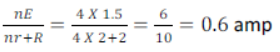
Current = 0.6 amp [ANS]
(ii) Cells connected in parallel,
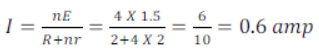
Current = 0.6 amp [ANS]
15) There resistors of 6 Ω , 3 Ω and 2 Ω are connected in parallel the combination of above resistors is connected in series to a resistance of 4 Ω and then to a cell of e.m.f 1.5 V If the internal resistance of cell is negligible .
(i) Draw the circuit diagram
(ii) Calculate the current in main circuit
(iii) Calculate the current in each of the resistor in parallel
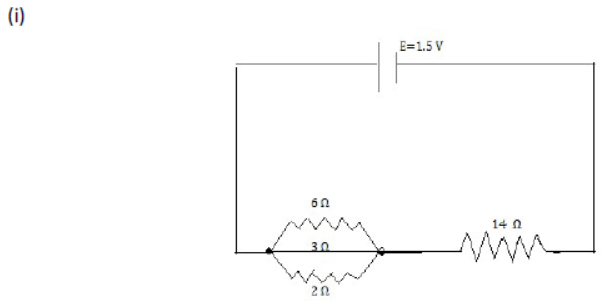
(ii) Equivalent resistance of 6 Ω, 3 Ω and 2 Ω in parallel
1/r1 = 1/6 + 1/3 + 1/2 = 6/6 = 1 R1 = 1Ω
So total equivalent resistance in series = 1+4= 5 Ω
Current in main circuit 𝐼 = V/R = 1.5/5 =0.3A [ANS]
= 0.3 𝐴 [ANS]
(iii) p.d. across parallel circuit; V = IR = 0.3 X 1 = 0.3 V
Current in 6 Ω resistor
I1 = V/R = 0.3/6 = 0.05 A[Ans.]
Similarly current in 3 Ω resistor
I2 = V/R = 0.3/3 = 0.10A [ANS]
Current in 2 Ω resistor
I3 = V/R = 0.3/3 = 0.15A [ANS]
16) Two resistors are connected in series as shown in the diagram.
(i) What is the current through the 5 ohm resistor?
(ii) What is the current through R?
(iii) What is the value of R? And
(iv) What is the value of V?
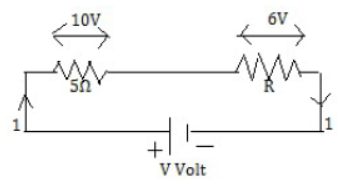
Given
Potential difference across 5 ohm resistor = 10 V
Potential difference across R ohm resistor = 6 V
Value of resistance R1= 5 ohm
I =? , R =? And V =?
By Ohm’s law the current through resistor of 5 ohm is
(i) 𝐼 = V/R = 10/5 = 2A [Ans]
(ii) Since the two resistors are connected in series therefore the current through resistor R is also 2 ampere [ANS]
(iii) Therefore value of R can be obtained as follows.
R = V/1 = 6/2 = 3 Ohm [ANS]
(iv) Since the resistors are in series therefore, net resistance of the circuit is
R=R1+R2=5+3=8 Ω
Hence by the expression of V=IR we have V= 2X8= 16V [ANS]
17) A letter A consist of a uniform wire of resistance 1 ohm per cm the sides of the letter are each 20cm long and the cross piece in the middle is 10 cm long (P-8.50). Find the resistance of the letter between points (i) BD and (ii) AB
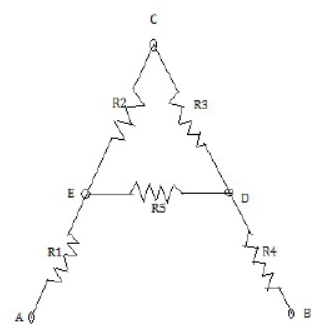
Clearly AE= EC=CD=DE=BD=10 CM
Therefore R1= R2 =R3 =R4 = R5 =10 Ω
As R2 and R3 are in series therefore their combined resistance is 10+10=20 Ohm This combination is in parallel with R5.
(i) Hence, resistance between points B and D is
1/R = 1/20 + 1/10 = 3/20 or R = 20/3 = 6.67Ω [ANS]
(ii) Now resistance R1, R and R4 are in series therefore resistance across AB is
R1= R+R1+ R4 = 20/3 + 10 +10 = 26.67Ω [ANS]
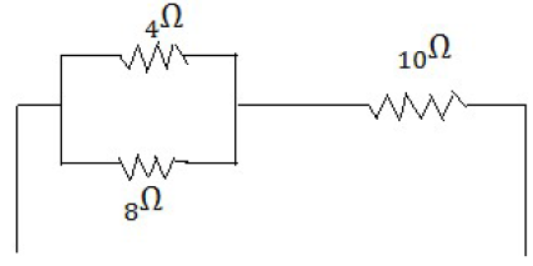
18) A circuit is made by connecting three resistances of 4 Ω,8 Ω and 10 Ω their total resistance is more than 10 Ω but less than 14 Ω show the circuit arrange on a diagram and calculate the equivalent resistance(1989 type)
We connect the resistance of 4 Ω and 8 Ω in parallel to each other and then connect this parallel combination to the 10 Ω resistance in series the required arrangement is as shown in Fig. the equivalent resistance of 4 Ω and 8 Ω in parallel is given by
1/R = 1/4 + 1/ 8 = 2+1 /8 = 3/8 OR R = 8/3Ω = 2.67Ω
Thus, the total resistance of the setup is (2-67+10) Ω = 12.67 Ω [ANS]
Fig
19) What is the equivalent resistance between the point X and Y for the network show given figure?
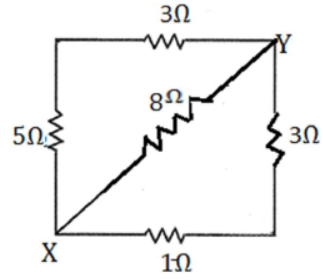
We can redraw the given circuit as
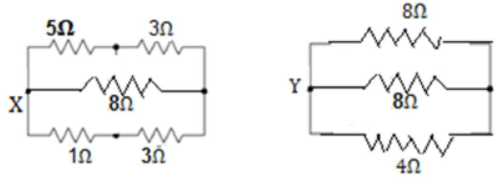
Hence, the required equivalent resistance R given by
1/R = 1/8 + 1/8 +1/4 = 1+1+2 / 8 = 4/8 =1/2
R= 2 Ω [ANS]
20) What is the usual color code followed for connecting live neutral and earth wires? Why is it so important?
The following is the color code.
Live wire- red, Neutral wire – black and earth wire – Green. This color code of electric wire must be followed, so that even a layman will be able to identify the correct connecting wire.
21) What is the resistance of an ideal ammeter?
The resistance of an ideal ammeter is zero.
22) Which one has more resistance – a 100 Walt bulb or 60 Walt bulbs?
The resistance of a 60 Walt bulb is more than the resistance of a 100 Walt bulb.
23) (a) What happens to the electrical resistance when mercury is cooled to 4.12 k? (b) What name is given to this phenomenon?
(a) When mercury is cooled to 4.12 k the electrical resistance of mercury disappears completely and becomes zero.
(b) This phenomenon of loss of electrical resistance of a substance on cooling it to an extremely low temperature is known as super conductivity.
24) Derive the formula for electric power which is used only when voltage V and resistance R are known to us.
We know that P= V X 1
From Ohm’s law, we have
V/I = 𝑅 … … … (𝑖)
Or V= IR
Or 𝐼 =V/I… … … . (𝑖𝑖)
Substituting the value of 1 in equation 1
We get P = 𝑉𝑋* V/R
or Power P =V2/R
25) A battery of emf 12V and internal resistance 2Ω is connected with two resistances A and B of resistance 4 Ω and 6 Ω respectively joined in series.
Find:
i. current in the circuit
ii. The terminal voltage of the cell
iii. The potential difference across 6 Ω Resistor
iv. Electrical energy spent per minute in 4 Ω resistors. (2016)
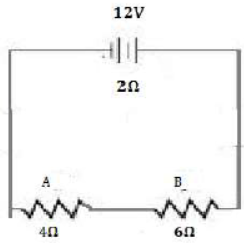
(i)Total resistance = (4.0+6.0+2.0) Ω = 12 Ω
Current in the circuit = V/R = 12/2 = 1𝐴 [ANS]
(ii) Terminal voltage of the cell V=IR = 1 X 10= 10V [ANS]
(iii)The potential difference across 6 Ω
Resistor = I X R = 1A X 6 Ω =6 V [ANS]
(iv) E= I2 RT = 1 X 4 X 60 – 240 I [ANS]
26) Find the equivalent resistance between point A and B. (2015)
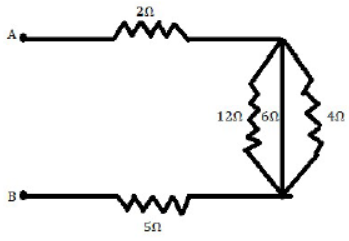
12 Ω, 6 Ω And 4 Ω are connection in parallel
Then 1/RP = 1/12Ω + 1/6Ω + 1/4Ω = 1+2+3 /12 = 1/2ΩRp = 2Ω
Now 2 Ω, 2 Ω and 5 Ω are combined in a series
Then equivalent resistance between point A and B, R= (2+2+5) =9 Ω [ANS]
27) A cell of E.m.f 2v and internal resistance 1.2 Ω is connected with an ammeter of resistance 0.8 Ω and two resistors of 4.5 Ω and 9 Ω as shown in the diagram below. (2015)
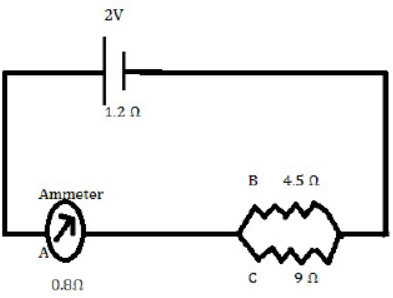
(i) What would be the reading on the ammeter?
(ii) What is the potential difference across the terminals of the cell?
Given E= 2V, r = 1.2 Ω
Resistance of resistor A= 0.8 Ω
Resistance of resistor B= 4.5 Ω
Resistance of resistor C=9 Ω
The resistors B and C are in parallel.
If the equivalent resistance is Rp then 1/RP = 1/4.5Ω + 1/9Ω = 2+1/9Ω = 1/3Ω rp = 3Ω
The resistor A is in series with resistance Rp
R= 0.8+3=3.8 Ω
Total resistance current draw from the battery = 3.8+1.2 = 5 Ω
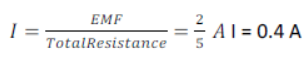
(i) The reading of Ammeter i= 0.4 A [ANS]
(ii) Terminal voltage of the cell V= IR = 0.4 X 308V = 1.52 V [ANS]
28) Find the equivalent resistance between points A and B?
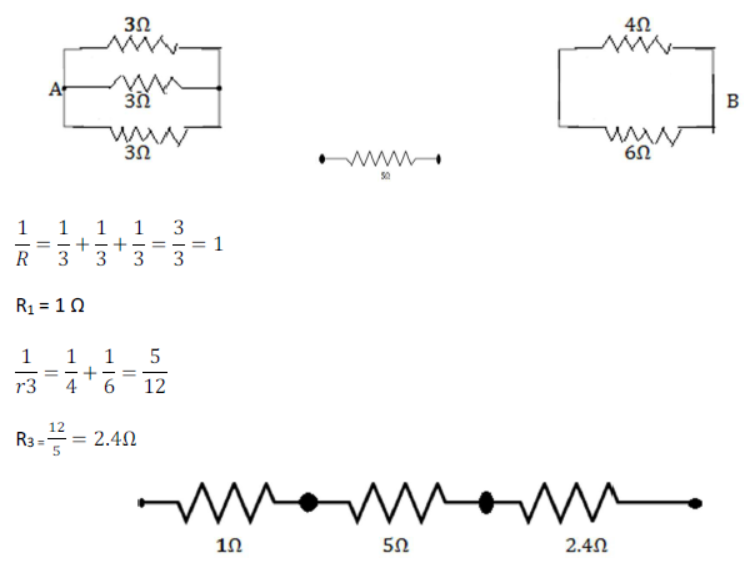
Equivalent resistance = (1+5+2.4) Ω = 8.4 Ω (Am) [ANS]
29) Two resistors of 4 Ω and 6 Ω are connected in parallel to a cell to draw 0.5 A current from the cell (2014)
(i) Draw a labeled circuit diagram showing the above arrangement
(ii) Calculate the current in each resistor.
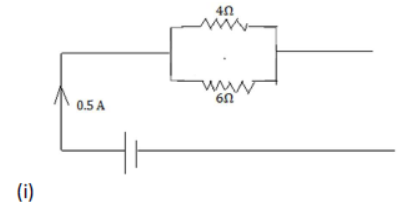
(ii) Let current through 4 Ω resistance is ‘i’
Then current through 6 Ω resistance is(0.5-i)
i X 4 = (0.5-i) X 6 or
4i=3-6i
Or 10i = 3 or i =0.3A
Current through 4 Ω resistance = 0.3 A and current through 6 Ω
= 0.5-0.3= 0.2 A (Am) [ANS]
30) A metal wire of resistance 6 Ω is stretched so that its length is increased to twice it original length, calculate its new resistance?
Volume of a metal wire remains same
A1 l1 = A2 l2
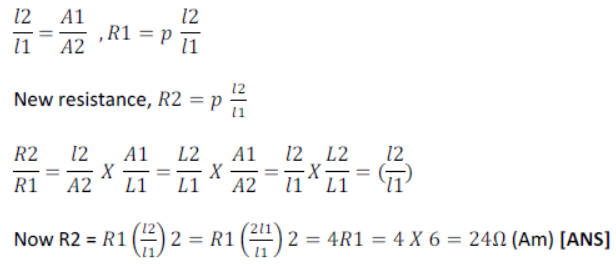
31) Calculate the equivalent resistance between the points A and B for the following combination of resistance
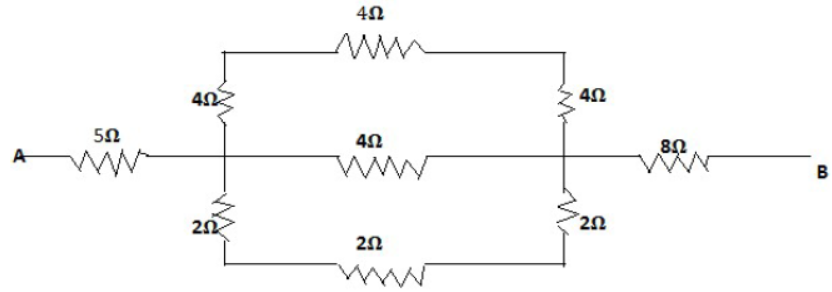
R1 = 4+4+4 = 12 Ω
R2 = 2+2+2 = 6 Ω
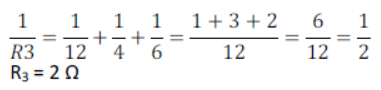
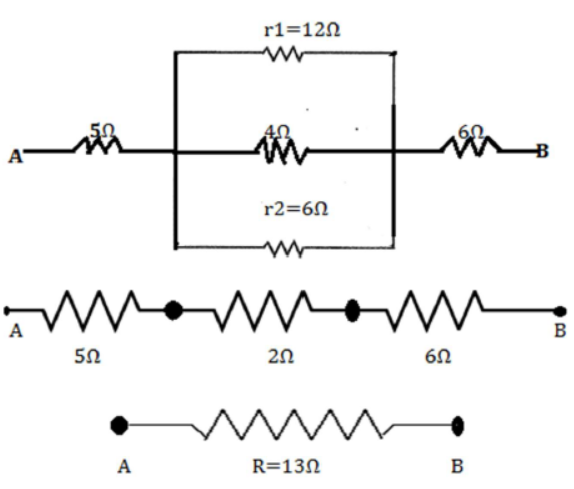
Resistance between A and B R=5+2+6= 13 Ω
Hence equivalent resistance between A and B = 13 Ω [ANS]
32) An electrical application is rated at 1000 KVA, 220 V if the application is operated for 2 hours calculate the energy consumed by the application in (i) kwh (ii) joule.
(i) E = power X Time=
1000 X 2 = 2000 kwh [ANS]
(ii) E = 2000 X 3.6 X 106 J
= 7.2 X 109 J [ANS]
33) Calculate the equivalent resistance between P and Q from the following diagram?
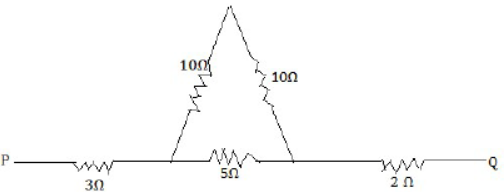
The two 10 Ω resistors are in series & parallel to 5 Ω equivalent resistance
1/R = 1/20 + 1/5 = 1+4/20 = 5/20 = 1/4R = 4Ω
Resistance between P and Q = 3+4+2= 9 Ω [ANS]
34) At what voltage is the alternating current supplied to our house?
220 to 240 V
35) Three resistors are connected to a 6 V batter as shown in the given figure (2011)
(i) Calculate the equivalent resistance of the circuit
(ii) Total current in the circuit
(iii) Potential difference across the 7.2 Ω resistor
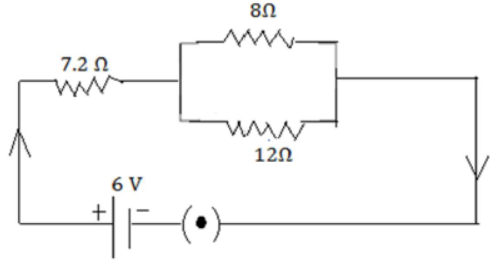
(i) 8 Ω and 12 Ω are in parallel, then equivalent resistance
1/R = 1/8 + 1/12 = 5/24 R=4.8
Now total resistance = 4.8+7.2= 12 Ω [ANS]
(ii) Let V= IR 𝐼 = V/R = 6/12 = 0.5A [ANS]
(iii) P.D across 7.2 Ω = 0.5 X 7.2= 3.6 V [ANS]
36) Calculate the equivalent resistance between A and B from the following diagram. (2011)
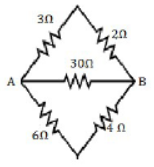
Let R be the equivalent resistance between A and b
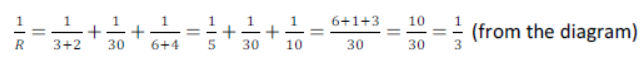
R = 3 Ω
The equivalent resistance between A and B is 3 Ω [ANS]
37) Three resistors are connected to a 12 V battery as shown in the Fig. given below.
(a) What is the current through the 8 Ohm resistance?
(b) What is the potential difference across the parallel combination of 6 Ohm and 12 ohm resistor?
(c) What is the current through the 6 Ohm Resistor? (2011)
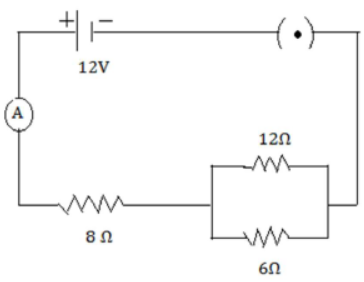
Let 12 Ω and 6 Ω resistors are in parallel.
Their effective resistance = 12X6 /12+ = 72/18 = 4Ω
Total resistance of the circuit = 8+4 = 12 Ω
So current drawn = 12/12 = 1A
(a) Current through 8 Ω resistor = 1 A [ANS]
(b) P.D. across 8 Ω resistor = 1 X 8=8 V
P.D. across the parallel combination of resistors = 12-8= 4 V
The resistances are in parallel they have the same P.D each i.e., 4 V [ANS]
(c) Current through the 6 Ω resistor 4/6 = 2/3 A= 0.67 𝐴 [ANS]
38) (a) An electric bulb is marked 100 250 V what information does this convey?
(b) How much current will the bulb draw if connected to a 250 v supply?
(a) It means that if a bulb is given a 250 volt supply, It will consume 100 J of energy in each second
(b) Let P = VI
I = 1000/250 =0.4 A [ANS]
39) Five resistors of different resistance are connected together as show in the figure A 12 v battery is connected to the arrangement calculate:
(a) The total resistance in the circuit
(b) The total current flowing in the circuit (2010)
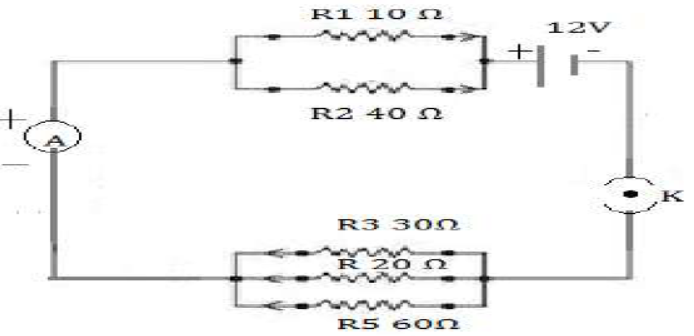
(a) Here R1 and R2 are parallel
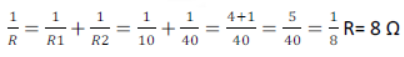
R3, R4, and R5 are in parallel
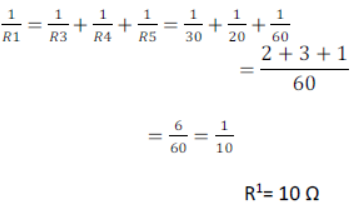
Total resistance = R+R1 = 8+10 = 18 Ω [ANS]
(b) Total current = Voltage / Total Resistance = 12/18 = 2/3 =67 A [ANS]
40) Six resistance are connected together as shown in the figure calculate the equivalent resistance between the point A and B.
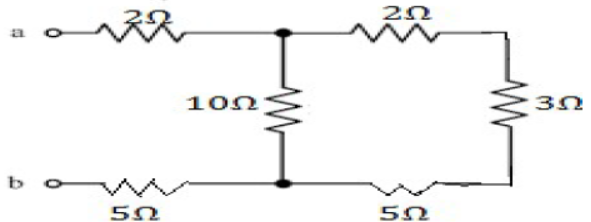
Equivalent resistance between A and B is = 2+R+5
Where 1/R = 1/10 + 1/10 = 2/10 = 1/5
Equivalent resistance between A and B = 2+5+2= 12 Ω [ANS]
41) The equivalent resistance of the following circuit diagram is 4 Ω calculate the value of 𝑥.
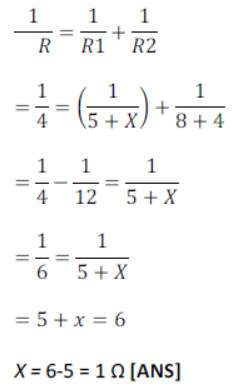
42) Three resistors of 6.0 Ω, 2.0 Ω and 4.0 Ω respectively are joined together as shown in the figure the resistors are connected to an ammeter and to a cell of e.m.f 6.0 V. (2007)
Calculate:
(a) Effective resistance of the circuit
(b) Current drawn from the cell
(a) Resistance R2 and R3 are in series so their effective resistance
R1 = 6 Ω
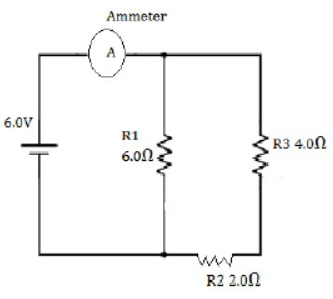
R1 and R1 are in parallel so 1/R = 1/R1 + 1/R1 = 1/+6 +1/6 = 2/6
R = 3 Ohm [ANS]
(b) V= IR or 6+ I X 3
I =6/3 = 2 amp. So current drawn from the cell is 2 amp. [ANS]
43) Calculate the value of the resistance which must be connected to a 15 Ω resistance to provide an effective resistance of 6 Ω Resistance decrease in parallel combination so let R resistance is connected to 15 W resistances in parallel to make resultant 6 W
Now, 1/6 = 1/15 +1/R
𝑜𝑟 1/R = 1/6 -1/15
= (5 -2)/30
= 3/30
= 1/10
R = 10 Ω [ANS]
44) A cell of e.m.f 1.5 V and internal resistance 1.0 w is connected to two resistors of 4.0 W and 20.0 in series as shown in the figure (2006)
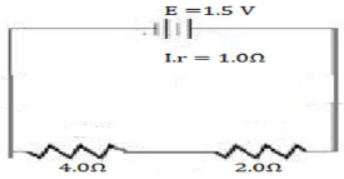
(i) Calculate the current in the circuit
(ii) Potential difference across the 4.0 Ohm resistor
(iii) Voltage drop when the current is flowing
(iv) Potential difference across the cell.
E.m.f of a cell = 1.5 volt
Internal resistance = 1.0 Ohm (r)
External resistance = r1+ r2( in series)
R= 4+20 = 24 Ω
(i) Current I = E/r+R or l = 1.5 / 1+24 = 1.5/25 = 0.6amp [ANS]
(ii) P.D across 4 Ω resistor = 4 X .06 = .24 Volt [ANS]
(iii) Voltage drop when the current is flowing = Ir = 06 X 1 = .06 Volt [ANS]
(iv) Potential difference across the cell = RI = 24 X .06 = 1.44 volt [ANS]
45) In the figure below, the ammeter A reads 0.3 A. Calculate:
(i) The total resistance of the circuit
(ii) The value of R
(iii) The current flowing through R. (2006)
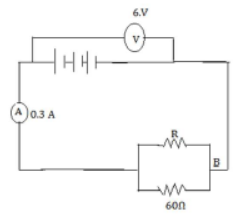
(i) Since V= IR
R=V/I = 6.0/0.3 = 20Ω
Total resistance = 20 Ω [ANS]
(ii) Given that resistance are in parallel
1/20 = 1/R + 1/60 or 1/R = 1/20 – 1/60
1/R = 3-1/60 = 2/60
R = 60/2 = 30Ω [ANS]
(iii) Since v= IR and potential (V) is equal at the two ends i.e. A and B
Let I be current flowing through R then (0.3-1) is current flowing through 60 Ωresistances
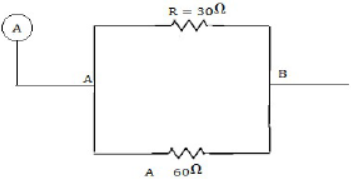
Now V= V → I1 R1 = I2 R2
I1 X 30 = (0.3- I1) X 60
I1 = 0.6 – 2 I, or 3 I1 = 0.6
or I1 = 0.6/3 = 0.2
Current flowing through R= 0.2 A [ANS]
46) A Wire of uniform thickness with a resistance of 27 Ω is cut into three equal pieces and they are joined in parallel. Find the resistance of the parallel combination.
Resistance of a given wire = 27 Ω
Resistance of each small wire = 17/3 = 9 Ω
Let Rp be the equivalent resistance for parallel combination
Then 1/Rp = 1/R1 + 1/R2 +1/R3 = 1/9+1/9+1/9
1/Rp = 3/9 or Rp = 9/3 = 3Ω
Resistance of the parallel combination = 3 Ω [ANS]
47) Mention two factor on which the resistance of wire depends (2005)
Resistance of a wire depends on
• length of a wire
• area of a cross- section of a wire
48) Four resistances of 2.0 Ω, each are joined end to end, to from a square ABCD. Calculate the equivalent resistance of the combination between any two adjacent corners.
The diagram indicates a square ABCD formed by joining four resistance of 2 Ω each end to end let us calculate the equivalent resistance of the combination between the two adjacent corner C and D.
Let us calculate the equivalent resistance of the combination between the two adjacent corners C and D. Arms DA AB and BC are joined in series so their equivalent resistance=
(2+2+2) Ω – 6 Ω now resistance of 6 Ω and 2 Ω are in parallel The equivalent resistance of the combination is R
Then, 1/R = 1/6+ 1/2 = 4/6 = 2/3
R= 3/2Ω = 1.5Ω[ANS]

49) In the fig given alongside A, B and C are three ammeters. The ammeter B reads 0.5 A (All the ammeter have negligible resistance )
Calculate:
(i) The reading in the ammeters A and C
(ii) The total resistance of the circuit
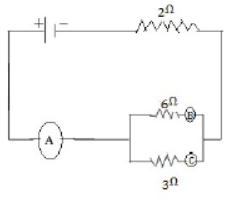
(i) P.D. across 6 Ω = P. D. across 3 Ω or 6 X 0.5 = 3 X i.e
Or i c i.e., current passing through the ammeter c is (6 X 0.5)/3 = 1.0 ampere [ANS]
(ii) Here 1/R = 1/6 + 1/3 = 3/6 = 1/2 𝑜𝑟 𝑅 = 2 Ω
Total resistance of the circuit = 2 Ω + r = 2 Ω + 2 Ω = 4 Ω
Current through A = Current passing through B+ current passing through C
Current through A = 0.5 +1.0 = 1.5 ampere. [ANS]
50) An electric bulb rated 220 V,60 W is working at fall efficiency
(i)State the resistance of the coil of the bulb
(ii) Another identical bulb is connected in series with the first one and the system is
connected across the main as shown in alongside.
• State the rate of conversion of energy in each bulb
• Calculate the total power
• What will be the total power if the bulbs are connected in parallel?
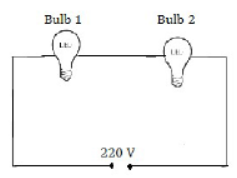
Given that potential difference = 220 V and power = 60W
Current I = power/p.d = 60/220 = 3/11amp
(i) Resistance of the bulb (R) = 220/ (3/11) = 806.7[ANS]
(ii) When another bulb is connected in series, then total resistance of two bulb becomes twice and current passing through the circuit
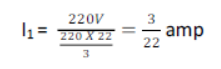
• Energy conversion in each bulb
=I2R =(3/22)/2 X (220X11/3)
= 15 watt [ANS]
• Energy conversion in the circuit in series combination
= V X I1 = 220 X 3/22 = 30watt [ANS]
• In parallel each bulb will consume 60 watt independently hence power consumption
will be = 60+60= 120 watt. [ANS]
51) A cell of e.m.f 1.5 V and internal resistance 10 Ohms is connected to a resistance of 5 Ohms, with an ammeter in series what is the reading of the ammeter?
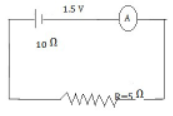
E= i (R+ r)
1.5 = I (5+10) or i= 1.5/1.5
I = 0.1 A [ANS]
52) Four cells each of e.m.f 1.5 V and internal resistance 2.0 Ohms are connected in parallel.
The battery of cells is connected to an external resistance of 2.5 Ohms. Calculate:
(i) The total resistance of the circuit
(ii) The current flowing in the external circuit and
(iii) The drop in potential across the terminals of the cells
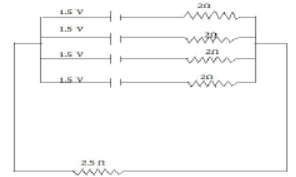
(i) As the four cells are connected in parallel their internal resistance i.e. r = 2 Ω will also be connected in parallel therefore, total internal resistance
1/rp = 1/r+1/r+1/r+1/r = 4/r = 4/2 = 2,
rp = 1/2 = 0.5Ω
Total resistance of the circuit R1
R + rp= 2.5 Ω + 0.5 Ω = 3.0 Ω [ANS]
(ii) The current flowing in the external circuit in parallel combination of the cells, the effective
e.m.f of any number of cells is equal to the e.m.f due to a single cell.
𝑖 = E/R Where E=1.5 V and R1 = 3.0 Ω
Current i = 1.5V /3.0Ω = 0.5 A [ANS]
(iii) The drop in potential across the terminal of a cell V= E- irp
= 1.5 V – 0.5 A X 0.5 Ω
= 1.5 V -0.25 V = 1.25 V [ANS]
Which is same across the terminal of every cell as the other specification of different cells are same
Or 𝑉
=ER/rp+R
= 1.5V X 2.5V / 0.5Ω+2.5Ω
=1.5V X 2.5Ω/3.0Ω
=1.25V(Am) [ANS]
53) In the figure shown below calculate (2000)
(i) The value of combined resistances of 40 Ohm and R using the reading of the two meters
(ii) The value of R
(iii) The current flowing through R
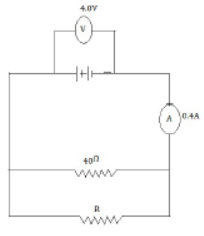
Given V= 4.0 V and I =0.4 A
(i) Therefore the total resistance of the circuit is R=V/I = 4.0/0.4 = 10 ohm [ANS]
(ii) Now R and 40 Ohm are connected in parallel and their combined resistance is 10 Ohm therefore we have
1/10 = 1/R+ 1/40 solving for R we have R = 40/3 = 13.3 ohm
(iii) Current flowing through R = 0.4 X 40 /40 +13.3 = 0.3A [ANS]
54) Define the e.m.f (E) of a cell and the potential difference (V) across a resistor (R) in terms of the work done in moving a unit charge
State the relating between these two works and the work done in moving a unit charge through a cell connected across the resistor. Take the internal resistance of the cell as ‘r’ hence obtains expression for the current ‘i’ in the circuit
E.M.F of a cell is generally define as the amount of work done (or the energy spent) in taking a unit positive charge around the complete circuit of the cell. It is also defined as the potential difference between the terminals of a cell when no current is drawn from it (or when the cell is an open circuit)
Potential difference (P .D) or the terminal voltage of a cell is generally defined as the amount of work done in carrying a unit positive charge round the circuit connected across the terminals of the cell.
If ‘W’ is the amount of work done (in J) in moving a test change ‘q’ between the terminals of a cell through a resistor ‘R’ then the
P.D = W/q i.e., work done in moving a unit positive change across the terminals of the cell.
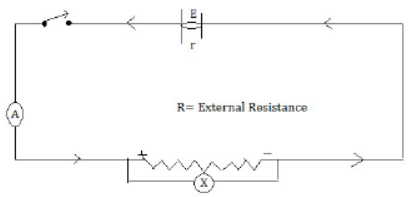
Relation between ‘E’, ‘V’ external resistance ‘R’ and the internal resistance ‘r’ Applying Ohm’s law to external resistance only ; I = V/R . . . . . 1
Again applying Ohm’s law to complete circuit I = E/R+r….2
Comparing Value of I in 1 and 2
We have V/R = E/ R+r
Or ER = v (R + r) = VR + Vr
ER-VR=Vr
Or R (E- V) = Vr
Or 𝑟 = R(E=V)/V = E-V /I
(V= IR)
Or I = E – V/I
55) A battery of e.m.f 9 V and internal resistance 0.6 ohm connected to three resistors A,B and C. (1995)
Calculate:
(i) The combined resistance B and c
(ii) The total resistance of A,B and C
(iii) The total resistance of the circuit
(iv) The current in each of the three resistance A,B and C
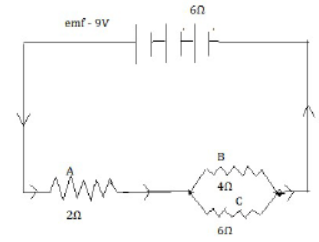
(i) Let R be the combined resistance of B and c which are connected in parallel we than have
1/R = 1/4 + 1/6 = 5/12 Or r= 2.4 ohm [ANS]
(ii) Now R and A are connected in series therefore the total resistance,
say Y of A, B and c is given by Y= A + R =(2+2.4)=4.4 ohm [ANS]
(iii) The total resistance say Z of the circuit, is given by
Z = (Y+06) Ω = (4.4+0.6) Ω = 5.0 Ω [ANS]
(iv) The current flowing in the circuit is
I = 9/Z = 9/5 = 1.8 A
This is also the current through the resistor A
Thus IA = 1.8 A
Now current through B and C is obtained by using the formula
IB = IRB/RB + RC = 1.8 X 4 /4+6 = 0.72 A
Ic = IRC/RB + RC = 1.8 X 4 /4+6 = 108/10 = 1.08 A [ANS]
56) Four cells each of e.m.f 2 V and internal resistance 0.1 Ohm are connected in series. The combination is connected in series to an ammeter of negligible resistance, a 1.6 Ohm resistor and an unknown resistor R1 the current in the circuit is 2A (1996)
Draw a labeled circuit diagram for the above arrangement and calculate:
(i) The total resistance in the circuit
(ii) The total e.m.f
(iii) The value of R1 and
(iv) The potential difference across R1
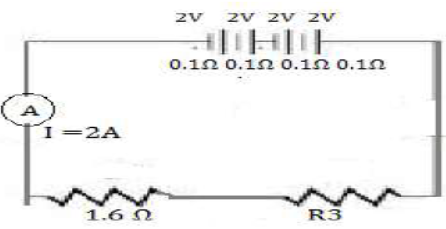
(i) Total resistance = 1.6+0.1 X 4+R1
= 1.6+0.4+R1 (2+R1) Ω
⸫ Total Resistance = R1+2 (2+2) Ω = 4 Ω. (solved after finding out R1) [ANS]
(ii) Total e.m.f = 2+2+2+2 =8V [ANS]
(iii) Here I = Total E.m.f / total resistance or 2 = 8/R1 + 2
Or, 2R1+4 =8 or 2R1 = 4 or R1=2 Ω. [ANS]
(iv)Potential difference across R1 = IR1 = 2 X 2 = 4V [ANS]
57) Two resistors of resistance 2 Ohm and 3 Ohm in parallel are connected to a cell of e.m.f 1.5 v and internal resistance 0.3 Ohm. Draw a labeled circuit diagram showing the above arrangement and the current drawn from the cell. (1997)
The circuit diagram is as shown below:
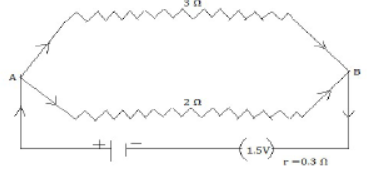
If total resistance between A and b id R, then
1/R = 1/2 + 1/3 = 5/6 or R = 6/5 = 1.2 Ohm
Now total resistance of the circuit is RT = R + 0.3
= 1.2 + 0.3 =1.5 Ohm
Hence current in the circuit is 𝐼 = V/RT = 1.5/1.5 = 1A [ANS]
58) Circuit diagram is given in which three resistances 1 Ohm, 2 Ohm and 3 Ohm are connected to cell of e.m.f 2 v and internal resistance 0.5 ohm
(i) Calculate the total resistance of the circuit
(ii) what is the reading of the ammeter?
(iii) What will be the ammeter reading if an exactly similar cell is connected in series with the given cell? (1994)
(i) The resistance 1 Ω and 2Ω are in series, 1 Ω +2 Ω = 3 Ω
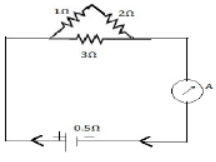
The combination is in parallel with the resistor of 3 Ohm
or 1/R1 = 1/3+1/3
R1=3/2 = 1.5
Total resistance is the circuit R = R1 + r = (1.5 + 0.5) Ω = 2.0 Ω [ANS]
(ii) I = V/R = 2/2 = 1A [ANS]
(iii) EMF of the cells = 4V
Total internal resistance of the cells = 1 Ω
Ammeter reading = 4/2.5= 1.6 A [ANS]
59) A cell supplies a current of 0.6 A through a 2 Ohm coil and a current of 0.3A through a 8 Ohm coil Calculate the e.m.f and the internal resistance of the cell.
Given I1= 0.6A, R1= 2Ω,
I2= 0.3 A, R2= 8 Ω, r =?
Using I = E/R+r
1) 0.6 = E/2+r and
2) 0.3 = E/8+r
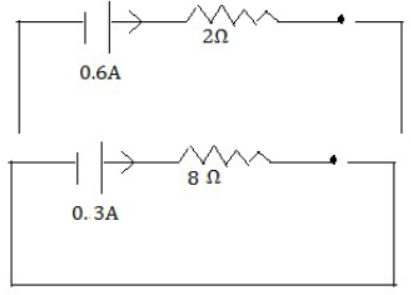
From the above two we have
As same cell is used
E is same so (i) = (ii)
0.6(2 + r) = 0.3 (8+ R)
Or 0.3r = 1.2 or r = 4Ohm
E= 0.6(2+4) (putting the value of r in eq. (i)
= 3.6 V [ANS]
60) From the given figure above calculate (1996)
(i) The equivalent resistance between P and Q
(ii) The reading of the ammeter
(iii) The electrical power between P and Q
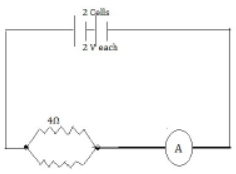
(i) if equivalent resistance is R, then
1/R = 1/4+ 1/6 = 3+2/12 = 5/12
Equivalent resistance R = 12/5 = 2.4Ω [ANS]
(ii) From diagram E= 2 X 2 = 4 V and R=2.4 Ω
But E = IR
4 = I X 2.4
I= 4/24 = 1.66 A [ANS]
(iii) P = I2R = (4/24) X 2.4 = 6.66 watts [ANS]
61) Write an expression for the resistance of a conducting wire in terms of its length and area of cross section
R= 𝑃 (1/A)
, where r = resistance
L= length and
A = Area of cross section of the wire
P = resistivity or specific resistance of the material of the wire.
62) Calculate the equivalent resistance of the following combination of resistors : r1 , r2 , r3, r4
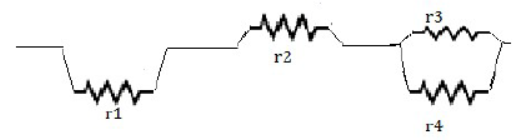
Resistance of r3, r4 in parallel is given by
1/r = 1/r3 + 1/r4 = r4+r3 / r3r4
R = r3+r4 / r3r4
Now resistance r1, r2 and r4 are in series their combined resistance R is given
R = r1 , r2 + r4+r3 / r3r4 = (r1 + r2)r3 + (r1 + r2 + r3)r4 / r3+r4 [ANS]

We hope you liked Current Electricity ICSE Class 10 Physics Notes and solutions. If you have any questions please post them in the comments section below


