Question 1. Find which of the following equations are quadratic:
(𝑖) (3𝑥– 1)2 = 5(𝑥 + 8)
(𝑖𝑖) 5𝑥2 – 8𝑥 = −3(7– 2𝑥)
(𝑖𝑖𝑖) (𝑥– 4)(3𝑥 + 1) = (3𝑥– 1)(𝑥 + 2)
(𝑖𝑣) 𝑥2 + 5𝑥– 5 = (𝑥– 3)2
(𝑣) 7𝑥3– 2𝑥2+ 10 = (2𝑥– 5)2
(𝑣𝑖) (𝑥 − 1)2 + (𝑥 + 2)2 + 3(𝑥 + 1) = 0
Solution:
(𝑖) (3𝑥– 1)2 = 5(𝑥 + 8)
We know that,
(𝑎 − 𝑏)2 = 𝑎2 − 2𝑎𝑏 + 𝑏2
(3𝑥)2 − 2(3𝑥)(1) + (1)2 = 5𝑥 + 40
9𝑥2 – 6𝑥 + 1 = 5𝑥 + 40
9𝑥2 – 6𝑥 − 5𝑥 = 40 − 1
9𝑥2 – 6𝑥 − 5𝑥 = 39
9𝑥2 – 11𝑥 – 39 = 0
Above equation is the form of 𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0
Hence, the given equation is a quadratic equation.
(𝑖𝑖) 5𝑥2 – 8𝑥 = −3(7– 2𝑥)
5𝑥2 – 8𝑥 = −21 + 6𝑥
5𝑥2 – 8𝑥 − 6𝑥 = −21
5𝑥2 – 14𝑥 + 21 = 0
5𝑥2– 14𝑥 + 21 = 0
Above equation is the form of 𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0
Hence, the given equation is a quadratic equation.
(𝑖𝑖𝑖) (𝑥 – 4)(3𝑥 + 1) = (3𝑥– 1)(𝑥 + 2)
(𝑥 – 4)(3𝑥 + 1) = (3𝑥– 1)(𝑥 + 2)
3𝑥2 + 𝑥 − 12𝑥 − 4 = 3𝑥2 + 6𝑥 − 𝑥 − 2
3𝑥2 − 11𝑥– 4 = 3𝑥2 + 5𝑥 – 2
−11𝑥– 5𝑥 = – 2 + 4
−16𝑥 = 2
−16𝑥 − 2 = 0
16𝑥 + 2 = 0
Above equation is not in the form of 𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0
Hence, the given equation is not a quadratic equation.
(𝑖𝑣) 𝑥2 + 5𝑥– 5 = (𝑥– 3)2
We know that,
(𝑎 − 𝑏)2 = 𝑎2 − 2𝑎𝑏 + 𝑏2
𝑥2 + 5𝑥– 5 = 𝑥2 − 2(𝑥)(3) + 32
𝑥2 + 5𝑥– 5 = 𝑥2 − 6𝑥 + 9
5𝑥 + 6𝑥 = 9 + 5
11𝑥 = 14
11𝑥– 14 = 0
Above equation is not in the form of 𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0
Hence, the given equation is not a quadratic equation.
(𝑣) 7𝑥3– 2𝑥2 + 10 = (2𝑥– 5)2
We know that,
(𝑎 − 𝑏)2 = 𝑎2 − 2𝑎𝑏 + 𝑏2
7𝑥3 – 2𝑥2 + 10 = (2𝑥)2 − 2(2𝑥)(5) + (5)2
7𝑥3 – 2𝑥2 + 10 = 4𝑥2 − 20𝑥 + 25
7𝑥3 – 2𝑥2 − 4𝑥2 + 10 + 20𝑥 − 25 = 0
7𝑥3– 6𝑥2 + 20𝑥– 15 = 0
Above equation is not in the form of 𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0
Hence, the given equation is not a quadratic equation.
(𝑣𝑖) (𝑥 − 1)2 + (𝑥 + 2)2 + 3(𝑥 + 1) = 0
We know that,
(𝑎 − 𝑏)2 = 𝑎2 − 2𝑎𝑏 + 𝑏2
(𝑎 + 𝑏)2 = 𝑎2 + 2𝑎𝑏 + 𝑏2
𝑥2 − 2(𝑥)(1) + (1)2 + 𝑥2 + 2(𝑥)(2) + 22 + 3𝑥 + 3 = 0
𝑥2 − 2𝑥 + 1 + 𝑥2 + 4𝑥 + 4 + 3𝑥 + 3 = 0
2𝑥2 + 5𝑥 + 8 = 0
Above equation is the form of 𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0
Hence, the given equation is a quadratic equation.
Question 2. (i) Is x = 5 a solution of the quadratic equation 𝑥2– 2𝑥– 15 = 0?
Solution:
It is given that,
𝑥2 − 2𝑥 – 15 = 0
𝑥 = 5
Put the value of x in given equation
L.H.S = (5)2 – 2(5) – 15
25 – 10 – 15 = 0
L.H.S = R.H.S
Thus, 𝑥 = 5 is a solution of the quadratic equation 𝑥2 − 2𝑥 – 15 = 0
Question 2. (ii) Is x = -3 a solution of the quadratic equation 2𝑥2 – 7𝑥 + 9 = 0?
Solution:
It is given that,
2𝑥2 – 7𝑥 + 9 = 0
𝑥 = −3
Put the value of x in given equation
L.H.S = 2(−3)2 – 7(−3) + 9
2(9) + 21 + 9
18 + 21 + 9 = 48
L.H.S. ≠ R.H.S
Thus, 𝑥 = −3 is not a solution of the quadratic equation 2𝑥2 – 7𝑥 + 9 = 0
Question 3. If √(2/3) is a solution of equation 3𝑥2 + mx + 2 = 0, find the value of m.
Solution:
It is given that,
3𝑥2 + mx + 2 = 0
x = √(2/3)
Put the value of x in given equation

Question 4. 2/3 and 1 are the solutions of equation 𝑚𝑥2 + 𝑛𝑥 + 6 = 0. Find the values of m and n.
Solution:
It is given that,
mx2 + nx + 6 = 0
Put the value of 𝑥 = 2/3 in the given equation.

4𝑚 + 6𝑛 + 54 = 0……………………(i)
Put the value of 𝑥 = 1 in the given equation.
𝑚(1)2 + 𝑛(1) + 6 = 0
𝑚 + 𝑛 + 6 = 0
𝑚 + 𝑛 + 6 = 0……………………(ii)
Get the value of 𝑚 from equation (ii)
𝑚 = −6 − 𝑛……………(iii)
Put the value of 𝑚 in equation (i)
4(−6 − 𝑛) + 6𝑛 + 54 = 0
−24 − 4𝑛 + 6𝑛 + 54 = 0
2𝑛 + 30 = 0
2𝑛 = −30
𝑛 = −30/2
𝑛 = −15
Put the value of 𝑛 in equation (iii)
𝑚 = −6 − (−15)
𝑚 = −6 + 15
𝑚 = 9
Hence, the value of 𝑛 is -15 and 𝑚 is 9.
Question 5. If 3 and -3 are the solutions of equation 𝑎𝑥2 + 𝑏𝑥– 9 = 0. Find the values of 𝑎 and 𝑏.
Solution:
It is given that,
𝑎𝑥2 + 𝑏𝑥– 9 = 0
Put the value of 𝑥 = 3 in the given equation.
𝑎(3)2 + 𝑏(3)– 9 = 0
9𝑎 + 3𝑏– 9 = 0
3(3𝑎 + 𝑏– 3) = 0
3𝑎 + 𝑏– 3 = 0………………..(i)
Put the value of 𝑥 = −3 in the given equation.
𝑎(−3)2 + 𝑏(−3)– 9 = 0
9𝑎 − 3𝑏– 9 = 0
3(3𝑎 − 𝑏– 3) = 0
3𝑎 − 𝑏– 3 = 0………………..(ii)
Get the value of 𝑎 from equation (ii)
𝑎 = 𝑏+3/3 ……………(iii)
Put the value of 𝑎 in equation (i)
3 (𝑏+3/3 ) + 𝑏– 3 = 0
𝑏 + 3 + 𝑏– 3 = 0
2𝑏 = 0
𝑏 = 0
Put the value of 𝑏 in equation (iii)
𝑎 = 0+3/3
𝑎 = 3/3
𝑎 = 1
Hence, the value of 𝑎 is 1 and 𝑏 is 0.
Exercise 5B
Question 1. Without solving, comment upon the nature of roots of each of the following equations:
(𝑖) 7𝑥2– 9𝑥 + 2 = 0
(𝑖𝑖) 6𝑥2– 13𝑥 + 4 = 0
(𝑖𝑖𝑖) 25𝑥2– 10𝑥 + 1 = 0
(𝑖𝑣) 𝑥2 + 2√3𝑥 – 9 = 0
(𝑣) 𝑥2– 𝑎𝑥– 𝑏2 = 0
(𝑣𝑖) 2𝑥2 + 8𝑥 + 9 = 0
Solution:
(i) It is given that,
7𝑥2– 9𝑥 + 2 = 0
𝑎 = 7
𝑏 = 9
𝑐 = 2
We know that by discriminate,
D = 𝑏2 − 4𝑎𝑐
D = (9)2 − 4(7)(2)
D = 81 − 56
D = 25
Here 𝐷 > 0 then given equation have two real and unequal roots.
(ii) It is given that,
6𝑥2– 13𝑥 + 4 = 0
𝑎 = 6
𝑏 = −13
𝑐 = 4
We know that by discriminate,
D = 𝑏2 − 4𝑎𝑐
D = (−13)2 − 4(6)(4)
D = 169 − 96
D = 73
Here 𝐷 > 0 then given equation have two real and unequal roots.
(iii) It is given that,
25𝑥2– 10𝑥 + 1 = 0
𝑎 = 25
𝑏 = −10
𝑐 = 1
We know that by discriminate,
D = 𝑏2 − 4𝑎𝑐
D = (−10)2 − 4(25)(1)
D = 100 − 100
D = 0
Here 𝐷 = 0 then given equation have two real and unequal roots.
(iv) It is given that,
𝑥2– 2√3𝑥 − 9 = 0
𝑎 = 1
𝑏 = −2√3
𝑐 = −9
We know that by discriminate,
D = 𝑏2 − 4𝑎𝑐
D = (−2√3)2 − 4(1)(−9)
D = 12 + 36
D = 48
Here 𝐷 > 0 then given equation have two real and unequal roots.
(v) It is given that,
𝑥2– 𝑎𝑥 − 𝑏2 = 0
𝑎 = 1
𝑏 = −𝑎
𝑐 = −𝑏2
We know that by discriminate,
D = 𝑏2 − 4𝑎𝑐
D = (−𝑎)2 − 4(1)(−𝑏2)
D = 𝑎2 + 4𝑏2
Here 𝐷 > 0 then given equation have two real and unequal roots.
(vi) It is given that,
2𝑥2– 8𝑥 − 9 = 0
𝑎 = 2
𝑏 = 8
𝑐 = 9
We know that by discriminate,
D = 𝑏2 − 4𝑎𝑐
D = (8)2 − 4(2)(9)
D = 𝑎2 + 4𝑏2
Here 𝐷 > 0 then given equation have two real and unequal roots.
Question 2. Find the value of p, if the following quadratic equation has equal roots: 4𝑥2– (𝑝– 2)𝑥 + 1 = 0
Solution:
It is given that,
Quadratic equation has equal roots. So, D = 0
4𝑥2– (𝑝– 2)𝑥 + 1 = 0
𝑎 = 4
𝑏 = −(𝑝 − 2)
𝑐 = 1
We know that by discriminate,
D = 𝑏2 − 4𝑎𝑐
0 = [−(𝑝 − 2)]2 − 4(4)(1)
0 = 𝑝2 − 2(𝑝)(2) + 4 − 16
0 = 𝑝2 − 4𝑝 + 4 − 16
0 = 𝑝2 − 4𝑝 − 12
By splitting the middle term
𝑝2 − 6𝑝 + 2𝑝 − 12 = 0
𝑝(𝑝 − 6) + 2(𝑝 − 6) = 0
(𝑝 + 2)(𝑝 − 6) = 0
Then
𝑝 + 2 = 0 𝑝 − 6 = 0
𝑝 = −2 𝑝 = 6
Question 3. Find the value of ‘p’, if the following quadratic equations have equal roots: 𝑥2 + (𝑝 – 3)𝑥 + 𝑝 = 0
Solution:
It is given that,
Quadratic equation has equal roots. So, D = 0
𝑥2 + (𝑝 – 3)𝑥 + 𝑝 = 0
𝑎 = 1
𝑏 = (𝑝– 3)
𝑐 = 𝑝
We know that by discriminate,
D = 𝑏2 − 4𝑎𝑐
0 = 𝑏2 − 4𝑎𝑐
(𝑝 − 3)2 − 4(1)(𝑝) = 0
(𝑝 − 3)2 − 4𝑝 = 0
𝑝2 + 9– 6𝑝– 4𝑝 = 0
𝑝2– 10𝑝 + 9 = 0
𝑝2 − 9𝑝– 𝑝 + 9 = 0
𝑝(𝑝– 9) – 1(𝑝– 9) = 0
(𝑝 − 9)(𝑝– 1) = 0
Then
𝑝 − 9 = 0 𝑝 − 1 = 0
𝑝 = 9 𝑝 = 1
Question 4. The equation 3𝑥2– 12𝑥 + (𝑛– 5) = 0 has equal roots. Find the value of n.
Solution:
It is given that,
Quadratic equation has equal roots. So, D = 0
3𝑥2– 12𝑥 + (𝑛– 5) = 0
𝑎 = 3
𝑏 = −12
𝑐 = (𝑛 − 5)
We know that by discriminate,
D = 𝑏2 − 4𝑎𝑐
0 = 𝑏2 − 4𝑎𝑐
(−12)2 − 4(3)(𝑛 − 5) = 0
144 − 12(𝑛 − 5) = 0
144 − 12𝑛 + 60 = 0
144 − 12𝑛 + 60 = 0
−12𝑛 + 204 = 0
−12𝑛 = −204
12𝑛 = 204
𝑛 = 204/12
𝑛 = 17
Hence, the value of 𝑛 is 17.
Question 5. Find the value of m, if the following equation has equal roots: (𝑚– 2)𝑥2– (5 + 𝑚)𝑥 + 16 = 0.
Solution:
It is given that,
Quadratic equation has equal roots. So, D = 0
(𝑚– 2)𝑥2– (5 + 𝑚)𝑥 + 16 = 0
𝑎 = (𝑚 − 2)
𝑏 = −(5 + 𝑚)
𝑐 = 16
We know that by discriminate,
D = 𝑏2 − 4𝑎𝑐
0 = 𝑏2 − 4𝑎𝑐
[−(5 + 𝑚)]2 − 4(𝑚 − 2)(16) = 0
(5)2 + 2(5)(𝑚) + 𝑚2 − 64𝑚 + 128 = 0
25 + 10𝑚 + 𝑚2 − 64𝑚 + 128 = 0
−54𝑚 + 𝑚2 + 153 = 0
𝑚2 − 54𝑚 + 153 = 0
𝑚2 − 51𝑚 − 3𝑚 + 153 = 0
𝑚(𝑚 − 51) − 3(𝑚 − 51) = 0
(𝑚 − 51)(𝑚 − 3) = 0
Then
𝑚 − 51 = 0 𝑚 − 3 = 0
𝑚 = 51 𝑚 = 3
Question 6. Find the value of p for which the equation 3𝑥2– 6𝑥 + 𝑘 = 0 has distinct and real roots.
Solution:
It is given that,
Quadratic equation has real roots. So, 𝐷 > 0
3𝑥2– 6𝑥 + 𝑘 = 0
𝑎 = 3
𝑏 = 6
𝑐 = 𝑘
We know that by discriminate,
D < 𝑏2 − 4𝑎𝑐
0 < 𝑏2 − 4𝑎𝑐
0 < (6)2 − 4(3)(𝑘)
0 < 36 − 12𝑘
12𝑘 < 36
𝑘 < 36/12
𝑘 < 3
Hence, the value of K is 3.
Exercise 5C
Question 1. Solve: 𝑥² – 10𝑥– 24 = 0
Solution:
It is given that,
𝑥² – 10𝑥– 24 = 0
By the splitting the middle term,
𝑥² – 12𝑥 + 2𝑥– 24 = 0
𝑥(𝑥 − 12) + 2(𝑥 − 12) = 0
(𝑥 + 2)(𝑥 − 12) = 0
Then
𝑥 + 2 = 0 𝑥 − 12 = 0
𝑚 = −2 𝑥 = 12
Question 2. Solve: 𝑥²– 16 = 0
Solution:
It is given that,
𝑥²– 16 = 0
𝑥²– (4)2 = 0
𝑥²– (4)2 = 0
We know that,
(𝑎2 − 𝑏2) = (𝑎 − 𝑏)(𝑎 + 𝑏)
(𝑥² − 42) = (𝑥 − 4)(𝑥 + 4)
(𝑥 − 4)(𝑥 + 4) = 0
Then
𝑥 − 4 = 0 𝑥 + 4 = 0
𝑥 = 4 𝑥 = −4
Question 3. Solve: 2𝑥² − 1/2 𝑥 = 0
Solution:
It is given that,

Question 4. Solve: 𝑥(𝑥– 5) = 24
Solution:
It is given that,
𝑥(𝑥– 5) = 24
𝑥² − 5𝑥 = 24
𝑥² − 5𝑥 − 24 = 0
By the splliting the middle term
𝑥² − 5𝑥 − 24 = 0
𝑥² − 8𝑥 + 3𝑥 − 24 = 0
𝑥(𝑥 − 8) + 3(𝑥 − 8) = 0
(𝑥 + 3)(𝑥 − 8) = 0
Then
𝑥 + 3 = 0 𝑥 − 8 = 0
𝑥 = −3 𝑥 = 8
Question 5. Solve: 9/2 𝑥 = 5 + 𝑥²
Solution:
It is given that, 9/2 𝑥 = 5 + 𝑥²
9𝑥 = 2(5 + 𝑥2)
9𝑥 = 10 + 2𝑥²
0 = 2𝑥² − 9𝑥 + 10
2𝑥² − 9𝑥 + 10 = 0
2𝑥² − 5𝑥 − 4𝑥 + 10 = 0
𝑥(2𝑥 − 5) − 2(2𝑥 − 5) = 0
(𝑥 − 2)(2𝑥 − 5) = 0
Then
𝑥 − 2 = 0 2𝑥 − 5 = 0
𝑥 = 2 𝑥 = 5/2
Question 6. Solve 6/𝑥 = 1 + 𝑥
Solution:
It is given that, 6/𝑥 = 1 + 𝑥
6 = 𝑥(1 + 𝑥)
6 = 𝑥 + 𝑥2
𝑥² + 𝑥 − 6 = 0
𝑥² + 3𝑥 − 2𝑥 − 6 = 0
𝑥(𝑥 + 3) − 2(𝑥 + 3) = 0
(𝑥 − 2)(𝑥 + 3) = 0
Than
𝑥 − 2 = 0 𝑥 + 3 = 0
𝑥 = 2 𝑥 = −3
Question 7. Solve: 𝑥 = 3𝑥 + 1/4𝑥
Solution:
It is given that,
𝑥 = 3𝑥+1/4𝑥
𝑥 × 4𝑥 = 3𝑥 + 1
4𝑥² − 3𝑥 − 1 = 0
4𝑥² − 4𝑥 + 𝑥 − 1 = 0
4𝑥(𝑥 − 1) − 1(𝑥 − 1) = 0
(4𝑥 − 1)(𝑥 − 1) = 0
than
4𝑥 − 1 = 0 𝑥 − 1 = 0
𝑥 = 1/4 𝑥 = 1
Question 8. Solve 𝑥 + 1/𝑥 = 2.5
Solution:
It is given that,
𝑥 + 1
𝑥 = 2.5
𝑥²+1/𝑥 = 2.5 (we can write 2.5 as 5/4)
𝑥²+1/𝑥 = 5/2
2(𝑥² + 1) = 5𝑥
2𝑥² + 2 = 5𝑥
2𝑥² − 5𝑥 + 2 = 0
2𝑥² − 4𝑥 − 𝑥 + 2 = 0
2𝑥(𝑥 − 2) − 1(𝑥 − 2) = 0
2𝑥(𝑥 − 2) − 1(𝑥 − 2) = 0
(2𝑥 − 1)(𝑥 − 2) = 0
than
2𝑥 − 1 = 0 𝑥 − 2 = 0
𝑥 = 1/2 𝑥 = 2
Question 9. Solve: (2𝑥– 3)² = 49
Solution:
It is given that,
(2𝑥– 3)² = 49
2𝑥– 3 = √49
2𝑥– 3 = ±7
Then
2𝑥 − 3 = 7 2𝑥 − 3 = −7
2𝑥 = 7 + 3 2𝑥 = −7 + 3
𝑥 = 10/2 𝑥 = −4/2
𝑥 = 5 𝑥 = −2
Question 10. Solve: 2(𝑥²– 6) = 3(𝑥 – 4)
Solution:
It is given that,
2(𝑥²– 6) = 3(𝑥 – 4)
2𝑥²– 12 = 3𝑥 – 12
2𝑥²– 3𝑥 = −12 + 12
2𝑥²– 3𝑥 = 0
𝑥(2𝑥– 3) = 0
Then
𝑥 = 0 2𝑥– 3 = 0
𝑥 = 3/2
Question 11. Solve: (𝑥 + 1)(2𝑥 + 8) = (𝑥 + 7)(𝑥 + 3)
Solution:
It is given that,
(𝑥 + 1)(2𝑥 + 8) = (𝑥 + 7)(𝑥 + 3)
2𝑥² + 8𝑥 + 2𝑥 + 8 = 𝑥² + 3𝑥 + 7𝑥 + 21
2𝑥² − 𝑥² + 8𝑥 + 2𝑥 − 3𝑥 − 7𝑥 + 8 − 21 = 0
𝑥² + 10𝑥 − 10𝑥 − 13 = 0
𝑥² − 13 = 0
(𝑥)2 + (√13)2 = 0
(𝑥)2 + (√13)2 = 0
(𝑥 + √13)(𝑥 − √13) = 0
Then
𝑥 + √13 = 0 𝑥 − √13 = 0
𝑥 = −√13 𝑥 = √13
Question 12. Solve: 𝑥²– (𝑎 + 𝑏)𝑥 + 𝑎𝑏 = 0
Solution:
It is given that,
𝑥²– (𝑎 + 𝑏)𝑥 + 𝑎𝑏 = 0
𝑥²– 𝑎𝑥 − 𝑏𝑥 + 𝑎𝑏 = 0
𝑥(𝑥– 𝑎) − 𝑏(𝑥 − 𝑎) = 0
(𝑥– 𝑎)(𝑥 − 𝑏) = 0
Then
𝑥 − 𝑎 = 0 𝑥 − 𝑏 = 0
𝑥 = 𝑎 𝑥 = 𝑏
Question 13. Solve: (𝑥 + 3)²– 4(𝑥 + 3)– 5 = 0
Solution:
It is given that,
(𝑥 + 3)²– 4(𝑥 + 3)– 5 = 0
We know that,
(𝑎 + 𝑏)2 = 𝑎2 + 𝑏2 + 2𝑎𝑏
𝑥2 + (3)2 + 2(𝑥) (3)– 4𝑥 − 12– 5 = 0
𝑥2 + 9 + 6𝑥– 4𝑥 − 17 = 0
𝑥2 + 2𝑥 − 8 = 0
𝑥2 + 4𝑥 − 2𝑥 − 8 = 0
𝑥(𝑥 + 4) − 2(𝑥 + 4) = 0
(𝑥 − 2)(𝑥 + 4) = 0
Than
𝑥 − 2 = 0 𝑥 + 4 = 0
𝑥 = 2 𝑥 = −4
Question 14. Solve: 4(2𝑥– 3)²– (2𝑥– 3) – 14 = 0
Solution:
It is given that,
4(2𝑥– 3)²– (2𝑥– 3) – 14 = 0
Let us assumed that,
2𝑥– 3 = 𝑦
4𝑦²– 𝑦 – 14 = 0
4𝑦²– 8𝑦 + 7𝑦 – 14 = 0
4𝑦(𝑦– 2) + 7(𝑦– 2) = 0
(4𝑦 + 7)(𝑦– 2) = 0
Than
4𝑦 + 7 = 0 𝑦– 2 = 0
𝑦 = − 7/4 𝑦 = 2

Question 15. Solve:

Solution:
It is given that,

(3𝑥 − 2)(𝑥 + 4) = (3𝑥 − 8) (2𝑥 − 3)
3𝑥2 + 12𝑥 − 2𝑥 − 8 = 6𝑥2 − 9𝑥 − 16𝑥 + 24
3𝑥2 − 6𝑥2 + 12𝑥 − 2𝑥 + 9𝑥 + 16𝑥 − 8 − 24 = 0
−3𝑥2 + 10𝑥 + 25𝑥 − 32 = 0
−3𝑥2 + 35𝑥 − 32 = 0
−(3𝑥2 − 35𝑥 + 32) = 0
3𝑥2 − 35𝑥 + 32 = 0
3𝑥2 − 32𝑥 − 3𝑥 + 32 = 0
𝑥(3𝑥 − 32) − 1(3𝑥 − 32) = 0
(𝑥 − 1)(3𝑥 − 32) = 0
Than
𝑥 − 1 = 0 3𝑥– 32 = 0
𝑦 = 1 3𝑥 = 32
𝑥 = 32/3
𝑥 = 10 (2/3)
Question 16. 2𝑥2– 9𝑥 + 10 = 0, 𝑊ℎ𝑒𝑛
(i) 𝑥 ∈ 𝑁
(ii) 𝑥 ∈ 𝑄
Solution:
It is given that,
2𝑥2– 9𝑥 + 10 = 0
2𝑥2– 5𝑥 − 4𝑥 + 10 = 0
𝑥(2𝑥– 5) − 2(2𝑥 − 5) = 0
(𝑥 − 2)(2𝑥– 5) = 0
Than
𝑥 − 2 = 0 2𝑥– 5 = 0
𝑦 = 2 2𝑥 = 5
𝑥 = 5/2
Question 17. Solve

Solution:
It is given that,

2(2𝑥2 + 18) = 5(𝑥2 − 9)
4𝑥2 + 36 = 5𝑥2 − 45
4𝑥2 − 5𝑥2 = −45 − 36
−𝑥2 = −81
𝑥2 − 81 = 0
𝑥2 − (9)2 = 0
(𝑥 − 9)(𝑥 + 9) = 0
Than
𝑥 − 9 = 0 𝑥 + 9 = 0
𝑦 = 9 𝑥 = −9
Question 18. Solve:

Solution:
It is given that,

(3𝑥 + 10) (2𝑥 + 1) = 4(𝑥2 + 5𝑥 + 6)
6𝑥2 + 3𝑥 + 20𝑥 + 10 = 4𝑥2 + 20𝑥 + 24
6𝑥2 + 23𝑥 + 10 − 4𝑥2 − 20𝑥 − 24 = 0
2𝑥2 + 3𝑥 − 14 = 0
2𝑥2 + 7𝑥 − 4𝑥 − 14 = 0
𝑥(2𝑥 + 7) − 2(2𝑥 + 7) = 0
(𝑥 − 2) (2𝑥 + 7) = 0
Than
𝑥 − 2 = 0 2𝑥 + 7 = 0
𝑥 = 2 2𝑥 = −7
𝑥 = − 7/2
Question 19. Solve:Q20. Solve:

Solution:
It is given that,

𝑥(2𝑥 + 36) = 4(𝑥2 + 4𝑥 − 12)
2𝑥2 + 36𝑥 = 4𝑥2 + 16𝑥 − 48
2𝑥2 − 4𝑥2 + 36𝑥 − 16𝑥 + 48 = 0
−2𝑥2 + 20𝑥 + 48 = 0
−2(𝑥2 − 10𝑥 − 24) = 0
𝑥2 − 10𝑥 − 24 = 0
𝑥2 − 12𝑥 + 2𝑥 − 24 = 0
𝑥(𝑥 − 12) + 2(𝑥 − 12) = 0
(𝑥 + 2) (𝑥 − 12) = 0
Than
𝑥 + 2 = 0 𝑥 − 12 = 0
𝑦 = −2 𝑥 = 12
Question 20. Solve:

Solution:
It is given that,

8(𝑥2 − 4) = 7(𝑥2 − 1)
8𝑥2 − 32 = 7𝑥2 − 7
8𝑥2 − 7𝑥2 = −7 + 32
𝑥2 = 25
𝑥2 = ±√25
𝑥 = ± 5
Question 21. Find the quadratic equation, whose solution set is:

Solution:
(i) It is given that,
The solution set is {3, 5}
𝑥 = 3 𝑥 = 5
𝑥 − 3 = 0 𝑥 − 5 = 0
(𝑥 − 3)(𝑥 − 5) = 0
𝑥2 − 5𝑥 − 3𝑥 + 15 = 0
𝑥2 − 8𝑥 + 15 = 0
Hence, the required equation is 𝑥2 − 8𝑥 + 15 = 0.
(ii) It is given that,
The solution set is {−2, 3}
𝑥 = −2 𝑥 = 3
𝑥 + 2 = 0 𝑥 − 3 = 0
(𝑥 + 2)(𝑥 − 3) = 0
𝑥2 − 3𝑥 + 2𝑥 − 6 = 0
𝑥2 − 𝑥 − 6 = 0
Hence, the required equation is 𝑥2 − 𝑥 − 6 = 0.
(iii) It is given that,
The solution set is {5, −4}
𝑥 = 5 𝑥 = −4
𝑥 − 5 = 0 𝑥 + 4 = 0
(𝑥 − 5)(𝑥 + 4) = 0
𝑥2 + 4𝑥 − 5𝑥 − 20 = 0
𝑥2 − 𝑥 − 20 = 0
Hence, the required equation is 𝑥2 − 𝑥 − 20 = 0.
(iv) It is given that,

𝑥 = −3 𝑥 = −2/5
𝑥 + 3 = 0 𝑥 + 2
5 = 0
5𝑥 + 2 = 0
(𝑥 + 3)(5𝑥 + 2) = 0
5𝑥2 + 2𝑥 + 15𝑥 + 6 = 0
5𝑥2 − 17𝑥 + 6 = 0
Hence, the required equation is 5𝑥2 − 17𝑥 + 6 = 0.
Question 22. Solve:

Solution:
It is given that,

15(6𝑥 − 𝑥2 + 9) = 3(6 − 𝑥)(12 + 2𝑥)
5(6𝑥 − 𝑥2 + 9) = (6 − 𝑥)(12 + 2𝑥)
5(6𝑥 − 𝑥2 + 9) = 72 + 12𝑥 − 12𝑥 − 2𝑥2
30𝑥 − 5𝑥2 + 45 = 72 + 12𝑥 − 12𝑥 − 2𝑥2
30𝑥 − 5𝑥2 + 45 = 72 − 2𝑥2
30𝑥 − 5𝑥2 + 2𝑥2 + 45 − 72 = 0
30𝑥 − 3𝑥2 + 27 = 0
−3𝑥2 + 30𝑥 + 27 = 0
−3(𝑥2 − 10𝑥 + 9) = 0
𝑥2 − 10𝑥 + 9 = 0
𝑥2 − 9𝑥 − 𝑥 + 9 = 0
𝑥(𝑥 − 9) − 1(𝑥 − 9) = 0
(𝑥 − 1)(𝑥 − 9) = 0
Than
𝑥 − 1 = 0 𝑥 − 9 = 0
𝑥 = 1 𝑥 = 9
Question 23. Solve the equation 9𝑥2 + 3𝑥/4 + 2 = 0, if possible, for real values of 𝑥.
Solution:
It is given that,

We can’t solve the given equation for 𝑥 since √−1143 isn’t possible.
Hence, there is no real value of 𝑥.
Question 24. Find the value of 𝑥, if 𝑎 + 1 = 0 and 𝑥2 + 𝑎𝑥– 6 = 0.
Solution:
It is given that,
𝑎 + 1 = 0
𝑎 = −1
Put the value of 𝑎 in given equation,
𝑥2 + 𝑎𝑥– 6 = 0
𝑥2 + 1𝑥– 6 = 0
𝑥2 + 𝑥– 6 = 0
𝑥2 − 3𝑥 + 2𝑥– 6 = 0
𝑥(𝑥 − 3) + 2(𝑥– 3) = 0
(𝑥 + 2)(𝑥 − 3) = 0
Than
𝑥 + 2 = 0 𝑥 − 3 = 0
𝑥 = −2 𝑥 = 3
Question 25. Find the value of 𝑥, if 𝑎 + 7 = 0; 𝑏 + 10 = 0 and 12𝑥2 = 𝑎𝑥– 𝑏.
Solution:
It is given that,
𝑎 + 7 = 0
𝑎 = −7
and
𝑏 + 10 = 0
𝑏 = −10
Put the value of 𝑎 and 𝑏 in the given equation,
12𝑥2 = 𝑎𝑥– 𝑏
12𝑥2 = (−7)𝑥– (−10)
12𝑥2 = −7𝑥 + 10
12𝑥2 + 7𝑥 − 10 = 0
12𝑥2 + 15𝑥 − 8𝑥 − 10 = 0
3𝑥(4𝑥 + 5) − 2(4𝑥 + 5) = 0
(3𝑥 − 2)(4𝑥 + 5) = 0
Than
3𝑥 − 2 = 0 4𝑥 + 5 = 0
𝑥 = 2/3 𝑥 = −(5/4)
Question 26. Use the substitution 𝑦 = 2𝑥 + 3 to solve for 𝑥, if 4(2𝑥 + 3)2– (2𝑥 + 3)– 14 = 0.
Solution:
It is given that,
𝑦 = 2𝑥 + 3…………….(i)
Put the value of (2𝑥 + 3) as 𝑦 in given equation,
4𝑦2– 𝑦– 14 = 0
4𝑦2 + 7𝑦 − 8𝑦– 14 = 0
𝑦(4𝑦 + 7) − 2(4𝑦 + 7) = 0
(𝑦 − 2)(4𝑦 + 7) = 0
Than
𝑦 − 2 = 0 4𝑦 + 7 = 0
𝑦 = 2 𝑦 = −(7/4)
Put the value of 𝑦 in equation (i)
𝑦 = 2
𝑦 = 2𝑥 + 3
2 = 2𝑥 + 3
2 − 3 = 2𝑥

Question 27. Without solving the quadratic equation 6𝑥2 – 𝑥 – 2 = 0, find whether 𝑥 = 2/3 is a solution of this equation or not.
Solution:
It is given that,
𝑥 = 2/3
Put the value 𝑥 in given equation,

Question 28. Determine whether 𝑥 = −1 is a root of the equation 𝑥2 – 3𝑥 + 2 = 0 or not.
Solution:
It is given that,
𝑥 = −1
Put the value 𝑥 in given equation,
𝑥2 – 3𝑥 + 2 = 0
(−1)2 – 3(−1) + 2 = 0
1 + 3 + 2 = 0
6 ≠ 0
L.H.S. ≠ R.H.S.
Hence, 𝑥 = −1 is not a solution of the given equation.
Question 29. If 𝑥 = 2/3 is a solution of the quadratic equation 7𝑥2 + 𝑚𝑥– 3 = 0; Find the value of m.
Solution:
It is given that,
𝑥 = 2/3
Put the value 𝑥 in given equation,
7𝑥2 + 𝑚𝑥 − 3 = 0

Question 30. If 𝑥 = −3 and 𝑥 = 2/3 are solutions of quadratic equation 𝑚𝑥2 + 7𝑥 + 𝑛 = 0, find the values of m and n.
Solution:
It is given that,
𝑥 = −3
Put the value of x in given equation,
𝑚𝑥2 + 7𝑥 + 𝑛 = 0
𝑚(−3)2 + 7(−3) + 𝑛 = 0
9𝑚 − 21 + 𝑛 = 0
9𝑚 + 𝑛 = 21_____________(i)
And
𝑥 = 2/3
Put the value of x in given equation,
𝑚𝑥2 + 7𝑥 + 𝑛 = 0

4𝑚 + 42 + 9𝑛 = 0
4𝑚 + 9𝑛 = −42_____________(ii)
From equation first get the value of 𝑛
9𝑚 + 𝑛 = 21
𝑛 = 21 − 9𝑚__(iii)
Value of n put in equation (ii)
4𝑚 + 9𝑛 = −42
4𝑚 + 9(21 − 9𝑚) = −42
4𝑚 + 189 − 81𝑚 = −42
4𝑚 − 81𝑚 = −42 − 189
−77𝑚 = −231
𝑚 = 231/77
𝑚 = 3
Put the value of 𝑚 in equation (iii)
𝑛 = 21 − 9𝑚
𝑛 = 21 − 9(3)
𝑛 = 21 − 27
𝑛 = −6
Question 31. If quadratic equation 𝑥2– (𝑚 + 1) 𝑥 + 6 = 0 has one root as 𝑥 = 3; find the value of m and
the root of the equation.
Solution:
It is given that,
𝑥 = 3
Put the value of 𝑥 in given equation,
𝑥2– (𝑚 + 1) 𝑥 + 6 = 0
(3)2– (𝑚 + 1) 3 + 6 = 0
9– 3𝑚 − 3 + 6 = 0
– 3𝑚 + 12 = 0
– 3𝑚 = −12
𝑚 = −12/−3
𝑚 = 4
Put the value of 𝑚 in given equation,
𝑥2– (𝑚 + 1) 𝑥 + 6 = 0
𝑥2– (4 + 1)𝑥 + 6 = 0
𝑥2– 5𝑥 + 6 = 0
𝑥2– 3𝑥 − 2𝑥 + 6 = 0
𝑥(𝑥– 3) − 2(𝑥 − 3) = 0
(𝑥 − 2)(𝑥 − 3) = 0
Than
𝑥 − 2 = 0 𝑥 − 3 = 0
𝑥 = 2 𝑥 = 3
Question 32. Given that 2 is a root of the equation 3𝑥²– 𝑝(𝑥 + 1) = 0 and that the equation 𝑝𝑥²– 𝑞𝑥 + 9 = 0 has equal roots, find the values of p and q.
Solution:
It is given that,
𝑥 = 2
Put the value of 𝑥 in given equation,
3(2)²– 𝑝(2 + 1) = 0
3(2)²– 𝑝(3) = 0
12– 3𝑝 = 0
– 3𝑝 = −12
𝑝 = 12/3
𝑝 = 4
Put the value of 𝑝 in other equation
𝑝𝑥²– 𝑞𝑥 + 9 = 0
4𝑥²– 𝑞𝑥 + 9 = 0
It is given that the roots are equal, we know
𝑏2 − 4𝑎𝑐 = 0
Here,
𝑎 = 4
𝑏 = −𝑞
𝑐 = 9
(−𝑞)2 − 4(4)(9) = 0
𝑞2 − 144 = 0
𝑞2 = 144
𝑞 = √144
𝑞 = 12
Hence, the value of 𝑝 and 𝑞 is 4 and 12 respectively.
Question 33. Solve:

Solution:
It is given that,

𝑥2 = 𝑎𝑏 + 𝑏2 + 𝑎2 + 𝑎𝑏
𝑥2 = 𝑎2 + 𝑏2 + 2𝑎𝑏
𝑥2 = (𝑎 + 𝑏)2
𝑥 = 𝑎 + 𝑏
Question 34. Solve:

Solution:
It is given that,

(600 + 𝑥)(𝑥 − 10) = 630𝑥
600𝑥 − 6000 + 𝑥2 − 10𝑥 = 630𝑥
600𝑥 − 6000 + 𝑥2 − 10𝑥 − 630𝑥 = 0
−6000 + 𝑥2 − 10𝑥 − 30𝑥 = 0
−6000 + 𝑥2 − 40𝑥 = 0
𝑥2 − 40𝑥 − 6000 = 0
𝑥2 − 100𝑥 + 60𝑥 − 6000 = 0
𝑥2 − 100𝑥 + 60𝑥 − 6000 = 0
𝑥(𝑥 − 100) + 60(𝑥 − 100) = 0
(𝑥 + 60)(𝑥 − 100) = 0
Than
𝑥 + 60 = 0 𝑥 − 100 = 0
𝑥 = −60 𝑥 = 100
Question 35. If −1 and 3 are the roots of 𝑥2 + 𝑝𝑥 + 𝑞 = 0, find the values of p and q.
Solution:
It is given that,
𝑥 = −1
Put the value of 𝑥 in given equation,
(−1)2 + 𝑝(−1) + 𝑞 = 0
1 − 𝑝 + 𝑞 = 0
−𝑝 + 𝑞 = −1_______________ (i)
Also
𝑥 = 3
Put the value of 𝑥 in given equation,
(3)2 + 𝑝(3) + 𝑞 = 0
9 + 3𝑝 + 𝑞 = 0
3𝑝 + 𝑞 = −9______________(ii)
From equation (i) we get the value of 𝑞
−𝑝 + 𝑞 = −1
𝑞 = −1 + 𝑝__ (iii)
Put the value of 𝑞 in equation (ii)
3𝑝 + (−1 + 𝑝) = −9
3𝑝 + 𝑝 = −9 + 1
4𝑝 = −8
𝑝 = − 8/4
𝑝 = −2
Put the value of 𝑝 in equation (iii)
𝑞 = −1 + 𝑝
𝑞 = −1 + (−2)
𝑞 = −1 − 2
𝑞 = −3
Hence, the value of 𝑝 is −2 and 𝑞 is −3.
Exercise 5D
Question 1. Solve each of the following equations using the formula:
(i) 𝑥2 − 6𝑥 = 27
(ii) 𝑥2 − 10𝑥 + 21 = 0
(iii) 𝑥2 + 6𝑥 − 10 = 0
(iv) 𝑥2 + 2𝑥 − 6 = 0
(v) 3𝑥2 + 2𝑥 − 1 = 0
(vi) 2𝑥2 + 7𝑥 + 5 = 0

Solution:
(i) 𝑥2 − 6𝑥 = 27
𝑥2 − 6𝑥 − 27 = 0
𝑎 = 1
𝑏 = −6
𝑐 = −27
By the quadratic formula,

(ii) 𝑥2 − 10𝑥 + 21 = 0
𝑎 = 1
𝑏 = −10
𝑐 = 21
By the quadratic formula,

(iii) 𝑥2 + 6𝑥 − 10 = 0
𝑎 = 1
𝑏 = 6
𝑐 = −10
By the quadratic formula,
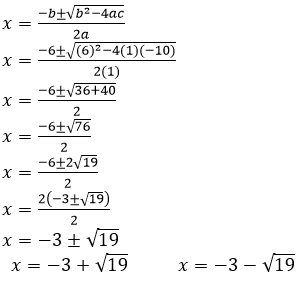
(iv) 𝑥2 + 2𝑥 − 6 = 0
𝑎 = 1
𝑏 = 2
𝑐 = −6
By the quadratic formula,

(v) 3𝑥2 + 2𝑥 − 1 = 0
𝑎 = 3
𝑏 = 2
𝑐 = −1
By the quadratic formula,

(vi) 2𝑥2 + 7𝑥 + 5 = 0
𝑎 = 2
𝑏 = 7
𝑐 = 5
By the quadratic formula,



(ix) 𝑥2 − 6 = 2√2𝑥
𝑥2 − 2√2𝑥 − 6 = 0
𝑎 = 1
𝑏 = −2√2
𝑐 = −6
By the quadratic formula,

(4 − 3𝑥)(2𝑥 + 3) = 5𝑥
(4 − 3𝑥)(2𝑥 + 3) = 5𝑥
8𝑥 + 12 − 6𝑥2 − 9𝑥 = 5𝑥
12 − 6𝑥2 − 𝑥 = 5𝑥
12 − 6𝑥2 − 𝑥 − 5𝑥 = 0
12 − 6𝑥2 − 6𝑥 = 0
−(6𝑥2 + 6𝑥 − 12) = 0
6𝑥2 + 6𝑥 − 12 = 0
6(𝑥2 + 𝑥 − 2) = 0
𝑥2 + 𝑥 − 2 = 0
𝑎 = 1
𝑏 = 1
𝑐 = −2
By the quadratic formula,


(xii) √6𝑥2 − 4𝑥 − 2√6 = 0
𝑎 = √6
𝑏 = −4
𝑐 = −2√6
By the quadratic formula,



3(2𝑥2 − 10𝑥 + 10) = 10(𝑥2 − 6𝑥 + 8)
6𝑥2 − 30𝑥 + 30 = 10𝑥2 − 60𝑥 + 80
6𝑥2 − 30𝑥 + 30 − 10𝑥2 + 60𝑥 − 80 = 0
−4𝑥2 − 30𝑥 + 50 = 0
−2(2𝑥2 − 15𝑥 + 25) = 0
2𝑥2 − 15𝑥 + 25 = 0
𝑎 = 2
𝑏 = −15
𝑐 = 25
By the quadratic formula,

Question 2. Solve each of the following equations for 𝑥 and give, in each case, your answer correct to one decimal place:
(𝑖) 𝑥2– 8𝑥 + 5 = 0
(𝑖𝑖) 5𝑥2 + 10𝑥– 3 = 0
Solution:
(i) 𝑥2– 8𝑥 + 5 = 0
𝑎 = 1
𝑏 = −8
𝑐 = 5
By the quadratic formula,

(ii) 5𝑥2 + 10𝑥 − 3 = 0
𝑎 = 5
𝑏 = 10
𝑐 = −3
By the quadratic formula,

Question 3 (i). Solve each of the following equations for x and give, in each case, your answer correct to two decimal places:
(𝑖) 2𝑥2– 10𝑥 + 5 = 0
Solution:
It is given that,
2𝑥2– 10𝑥 + 5 = 0
𝑎 = 2
𝑏 = −10
𝑐 = 5
By the quadratic formula,

Question 3 (ii). Solve each of the following equations for x and give, in each case, your answer correct to two decimal places:
4𝑥 + 6/𝑥 + 13 = 0

Question 3 (iii). Solve each of the following equations for x and give, in each case, your answer correct to two decimal places:
𝑥2 – 3𝑥– 9 = 0
Solution:
It is given that,
𝑥2 – 3𝑥– 9 = 0
𝑎 = 1
𝑏 = −3
𝑐 = −9
By the quadratic formula,

Question 3 (iv). Solve each of the following equations for x and give, in each case, your answer correct to two decimal places:
𝑥2– 5𝑥– 10 = 0
Solution:
It is given that,
𝑥2– 5𝑥– 10 = 0
𝑎 = 1
𝑏 = −5
𝑐 = −10
By the quadratic formula,
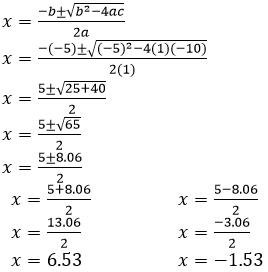
Question 4. Solve each of the following equations for x and give, in each case, your answer correct to 3 decimal places:
(𝑖) 3𝑥2– 12𝑥 – 1 = 0
(𝑖𝑖) 𝑥2– 16 𝑥 + 6 = 0
(𝑖𝑖𝑖) 2𝑥2 + 11𝑥 + 4 = 0
Solution:
(𝑖) 3𝑥2– 12𝑥 – 1 = 0
𝑎 = 3
𝑏 = −12
𝑐 = −1
By the quadratic formula,

(𝑖𝑖) 𝑥2– 16 𝑥 + 6 = 0
𝑎 = 1
𝑏 = −16
𝑐 = 6
By the quadratic formula,

(𝑖𝑖𝑖) 2𝑥2 + 11𝑥 + 4 = 0
𝑎 = 2
𝑏 = 11
𝑐 = 4
By the quadratic formula,

Question 5. Solve:
(𝑖) 𝑥4 – 2𝑥2 – 3 = 0
(𝑖𝑖) 𝑥4 – 10𝑥2 + 9 = 0
Solution:
(𝑖) 𝑥4 – 2𝑥2 – 3 = 0
By splitting the middle term method,
𝑥4 – 3𝑥2 + 𝑥2 − 3 = 0
𝑥2(𝑥2 − 3) + 1(𝑥2 − 3) = 0
(𝑥2 + 1)(𝑥2 − 3) = 0
𝑥2 + 1 = 0 𝑥2 − 3 = 0
𝑥2 = −1 𝑥 = ±√3
(𝑖𝑖) 𝑥2 – 10𝑥2 + 9 = 0
By splitting the middle term method,
𝑥4 – 9𝑥2 − 𝑥2 − 9 = 0
𝑥2(𝑥2 − 9) + 1(𝑥2 − 9) = 0
(𝑥2 + 1)(𝑥2 − 9) = 0
𝑥2 + 1 = 0 𝑥2 − 9 = 0
𝑥2 = −1 𝑥2 = 9
𝑥 = ±3
Question 6. Solve:
(𝑖) (𝑥2 – 𝑥)2 + 5(𝑥2– 𝑥) + 4 = 0
(𝑖𝑖) (𝑥2 – 3𝑥)2 – 16(𝑥2– 3𝑥)– 36 = 0
Solution:
(𝑖) (𝑥2 – 𝑥)2 + 5(𝑥2– 𝑥) + 4 = 0
Let us assumed that,
𝑥2 – 𝑥 = 𝑦
𝑦2 + 5𝑦 + 4 = 0
By the splitting the middle term
𝑦2 + 4𝑦 + 𝑦 + 4 = 0
𝑦(𝑦 + 4) + 1(𝑦 + 4) = 0
(𝑦 + 1)(𝑦 + 4) = 0
𝑦 + 1 = 0 𝑦 + 4 = 0
𝑦 = −1 𝑦 = −4
Put the value of y as −1
𝑥2 – 𝑥 = −1
𝑥2 – 𝑥 + 1 = 0
By the quadratic formula,
𝑎 = 1
𝑏 = −1
𝑐 = 1

(𝑖𝑖) (𝑥2 – 3𝑥)2 – 16(𝑥2– 3𝑥)– 36 = 0
Let us assumed that,
𝑥2 – 3𝑥 = 𝑦
𝑦2 − 16𝑦 − 36 = 0
By the splitting the middle term
𝑦2 – 16𝑦– 36 = 0
𝑦2– 18𝑦 + 2𝑦– 36 = 0
𝑦(𝑦– 18) + 2(𝑦– 18) = 0
(𝑦 + 2)(𝑦– 18) = 0
𝑦 + 2 = 0 𝑦– 18 = 0
𝑦 = −2 𝑦 = 18
Put the value of y as −2
𝑥2 – 3𝑥 = −2
𝑥2 – 3𝑥 + 2 = 0
By the quadratic formula,
𝑎 = 1
𝑏 = −3
𝑐 = 2
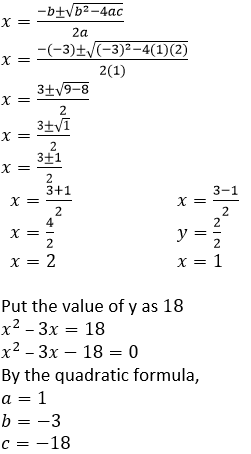

Question 7. Solve:-






Question 8. Solve the equation 2𝑥 − (1/𝑥) = 7. Write your answer correct to two decimal places.
Solution:
It is given that,

Question 9. Solve the following equation and give your answer correct to 3 significant figures:
5𝑥²– 3𝑥 – 4 = 0
Solution:
It is given that,
5𝑥²– 3𝑥 – 4 = 0
By quadratic formula
𝑎 = 5
𝑏 = −3
𝑐 = −4

Question 10. Solve for x using the quadratic formula. Write your answer correct to two significant figures.
(𝑥– 1)2– 3𝑥 + 4 = 0
Solution:
It is given that,
(𝑥– 1)2– 3𝑥 + 4 = 0
𝑥2 − 2(𝑥)(1) + 1– 3𝑥 + 4 = 0
𝑥2 − 5𝑥 + 5 = 0
By quadratic formula
𝑎 = 1
𝑏 = −5
𝑐 = 5

Question 11. Solve the quadratic equation 𝑥²– 3(𝑥 + 3) = 0; Give your answer correct to two significant figures.
Solution:
It is given that,
𝑥²– 3(𝑥 + 3) = 0
𝑥²– 3𝑥 − 9 = 0
By quadratic formula
𝑎 = 1
𝑏 = −3
𝑐 = −9

Exercise 5E
Question 1. Solve:
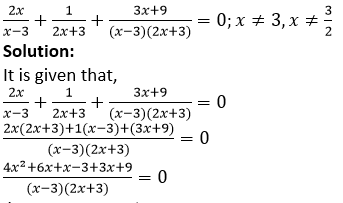
4𝑥2 + 6𝑥 + 𝑥 − 3 + 3𝑥 + 9 = 0
4𝑥2 + 10𝑥 + 6 = 0
By the splitting the middle term
4𝑥2 + 4𝑥 + 6𝑥 + 6 = 0
4𝑥(𝑥 + 1) + 6(𝑥 + 1) = 0
(4𝑥 + 6)(𝑥 + 1) = 0
4𝑥 + 6 = 0 𝑥 + 1 = 0
4𝑥 = −6 𝑥 = −1
𝑥 = −6/4
𝑥 = −3/2
Question 2. Solve: (2𝑥 + 3)2 = 81
Solution:
It is given that,
(2𝑥 + 3)2 = 81
2𝑥 + 3 = √81
2𝑥 + 3 = ±9
2𝑥 + 3 = 9 2𝑥 + 3 = −9
2𝑥 = 9 − 3 2𝑥 = −9 − 3
2𝑥 = 6 2𝑥 = −12
𝑥 = 6/2 𝑥 = −12/2
𝑥 = 3 𝑥 = −6
Question 3. Solve: 𝑎²𝑥²– 𝑏² = 0
Solution:
It is given that,
𝑎²𝑥²– 𝑏² = 0
(𝑎𝑥)2– 𝑏² = 0
We know that,
𝑎2 − 𝑏2 = (𝑎 + 𝑏)(𝑎 − 𝑏)
(𝑎𝑥)2– 𝑏² = 0
(𝑎𝑥 + 𝑏)(𝑎𝑥 − 𝑏) = 0
𝑎𝑥 + 𝑏 = 0 𝑎𝑥 − 𝑏 = 0
𝑎𝑥 = −𝑏 𝑎𝑥 = 𝑏
𝑥 = −𝑏/𝑎 𝑥 = 𝑏/𝑎
Question 4. Solve:

Question 5. Solve: 𝑥 + 4/𝑥 = −4; 𝑥 ≠ 0
Solution:
It is given that,
𝑥 + 4/𝑥 = −4
By the LCM of denominator,
𝑥2 + 4/𝑥 = −4
𝑥2 + 4 = −4𝑥
𝑥2 + 4𝑥 + 4 = 0
By splitting the middle term
𝑥2 + 4𝑥 + 4 = 0
𝑥2 + 2𝑥 + 2𝑥 + 4 = 0
𝑥(𝑥 + 2) + 2(𝑥 + 2) = 0
(𝑥 + 2)(𝑥 + 2) = 0
𝑥 + 2 = 0
𝑥 = −2
Hence, the value of 𝑥 is −2.
Question 6. Solve: 2𝑥4– 5𝑥² + 3 = 0
Solution:
It is given that,
2𝑥4– 5𝑥² + 3 = 0
2𝑥4– 3𝑥² − 2𝑥² + 3 = 0
𝑥²(2𝑥2– 3) − 1(2𝑥2 + 3) = 0
(𝑥² − 1)(2𝑥2– 3) = 0
𝑥² − 1 = 0 2𝑥2– 3 = 0

Q7. Solve: 𝑥4– 2𝑥²– 3 = 0.
Solution:
It is given that,
𝑥4– 2𝑥²– 3 = 0
𝑥4– 3𝑥² + 𝑥²– 3 = 0
𝑥2(𝑥2– 3) + 1(𝑥2– 3) = 0
(𝑥2 + 1)(𝑥2– 3) = 0
𝑥2 + 1 = 0 𝑥2– 3 = 0
𝑥² = −1 𝑥2 = 3
𝑥 = √−1 𝑥 = ±√3𝑥2
Question 8. Solve:

Put the values,
9(𝑦2 − 2) − 9𝑦 − 52 = 0
9𝑦2 − 18 − 9𝑦 − 52 = 0
9𝑦2 − 9𝑦 − 70 = 0
9𝑦2 − 30𝑦 + 21𝑦 − 70 = 0
3𝑦(3𝑦 − 10) + 7(3𝑦 − 10) = 0
(3𝑦 + 7)(3𝑦 − 10) = 0
3𝑦 + 7 = 0 3𝑦 − 10 = 0
3𝑦 = −7 3𝑦 = 10
𝑦 = −7/3 𝑦 = 10/3
Put the value of y as -7/3

3(𝑥2 + 1) = 10𝑥
3𝑥2 + 3 = 10𝑥
3𝑥2 − 10𝑥 + 3 = 0
By the splitting the middle term
3𝑥2 − 9𝑥 − 𝑥 + 3 = 0
3𝑥(𝑥 − 3) − 1(𝑥 − 3) = 0
(3𝑥 − 1)(𝑥 − 3) = 0
3𝑥 − 1 = 0 𝑥 − 3 = 0
3𝑥 = 1 𝑥 = 3
𝑥 = 1/3
Hence, the value of 𝑥 is 3.
Question 9. Solve:

Put the values,
2(𝑦2 − 2) − 𝑦 = 11
2𝑦2 − 4 − 𝑦 = 11
2𝑦2 − 4 − 𝑦 − 11 = 0
2𝑦2 − 𝑦 − 15 = 0
By splitting term,
2𝑦2 − 6𝑦 + 5𝑦 − 15 = 0
2𝑦(𝑦 − 3) + 5(𝑦 − 3) = 0
(2𝑦 + 5)(𝑦 − 3) = 0
2𝑦 + 5 = 0 𝑦 − 3 = 0
𝑦 = − 5/2 𝑦 = 3
Put the value of 𝑦 as 3

𝑥2 + 1 = − 5
2 × 𝑥
2(𝑥2 + 1) = −5𝑥
2𝑥2 + 2 = −5𝑥
2𝑥2 + 5𝑥 + 2 = 0
2𝑥2 + 4𝑥 + 𝑥 + 2 = 0
2𝑥(𝑥 + 2) + 1(𝑥 + 2) = 0
(2𝑥 + 1)(𝑥 + 2) = 0
2𝑥 + 1 = 0 𝑥 + 2 = 0
2𝑥 = −1 𝑥 = −2
𝑥 = − 1/2
Question 10. Solve:


Question 11. Solve: (𝑥² + 5𝑥 + 4)(𝑥² + 5𝑥 + 6) = 120
Solution:
It is given that,
(𝑥² + 5𝑥 + 4)(𝑥² + 5𝑥 + 6) = 120
Let us assumed that,
𝑥² + 5𝑥 = 𝑦 …………..(i)
(𝑦 + 4)(𝑦 + 6) = 120
𝑦2 + 6𝑦 + 4𝑦 + 24 = 120
𝑦2 + 10𝑦 + 24 = 120
𝑦2 + 10𝑦 + 24 − 120 = 0
𝑦2 + 10𝑦 − 96 = 0
𝑦2 + 16𝑦 − 6𝑦 − 96 = 0
𝑦(𝑦 + 16) − 6(𝑦 + 16) = 0
(𝑦 − 6)(𝑦 + 16) = 0
𝑦 − 6 = 0 𝑦 + 16 = 0
𝑦 = 6 𝑦 = −16
Put the value of 𝑦 as 6 in equation (i)
𝑥² + 5𝑥 = 6
𝑥² + 5𝑥 − 6 = 0
𝑥² + 6𝑥 − 𝑥 − 6 = 0
𝑥(𝑥 + 6) − 1(𝑥 + 6) = 0
(𝑥 + 6)(𝑥 − 1) = 0
(𝑥 + 6)(𝑥 − 1) = 0
𝑥 + 6 = 0 𝑥 − 1 = 0
𝑦 = −6 𝑥 = 1
Put the value of 𝑦 as -16 in equation (i)
𝑥² + 5𝑥 = −16
𝑥² + 5𝑥 + 16 = 0
By quadratic formula
𝑎 = 1
𝑏 = 5
𝑐 = 16

Question 12. Solve each of the following equations, giving answer upto two decimal places.
(𝑖) 𝑥2 – 5𝑥 − 10 = 0
(𝑖𝑖) 3𝑥2 – 𝑥– 7 = 0
Solution:
(i) 𝑥2 – 5𝑥 − 10 = 0
By quadratic formula
𝑎 = 1
𝑏 = −5
𝑐 = −10

(𝑖𝑖) 3𝑥2 – 𝑥– 7 = 0
By quadratic formula
𝑎 = 3
𝑏 = −1
𝑐 = −7

Question 13. Solve:

𝑦2 − 7𝑦 + 12 = 0
By splitting the middle term,
𝑦2 − 4𝑦 − 3𝑦 + 12 = 0
𝑦(𝑦 − 4) − 3(𝑦 − 4) = 0
(𝑦 − 3)(𝑦 − 4) = 0
𝑦 − 3 = 0 𝑦 − 4 = 0
𝑦 = 3 𝑦 = 4
Put the value of 𝑦 as 3 in equation (i)
𝑥/𝑥+2 = 3
𝑥 = 3(𝑥 + 2)
𝑥 = 3𝑥 + 6
𝑥 − 3𝑥 = 6
−2𝑥 = 6
𝑥 = − 6/2
𝑥 = −3
Put the value of 𝑦 as 4 in equation (i)
𝑥/𝑥+2 = 4
𝑥 = 4(𝑥 + 2)
𝑥 = 4𝑥 + 8
𝑥 − 4𝑥 = 8
−3𝑥 = 8
𝑥 = − 8/3
Question 14. Solve:
(𝑖) 𝑥2– 11𝑥 – 12 = 0; 𝑤ℎ𝑒𝑛 𝑥 ∈ 𝑁
(𝑖𝑖) 𝑥2 – 4𝑥 – 12 = 0; 𝑤ℎ𝑒𝑛 𝑥 ∈ 𝐼
(𝑖𝑖𝑖) 2𝑥2 – 9𝑥 + 10 = 0; 𝑤ℎ𝑒𝑛 𝑥 ∈ 𝑄
Solution:
(i) 𝑥2– 11𝑥 – 12 = 0
By splitting the middle term,
𝑥2– 12𝑥 + 𝑥 – 12 = 0
𝑥(𝑥– 12) + 1(𝑥 – 12) = 0
(𝑥 + 1)(𝑥– 12) = 0
𝑥 + 1 = 0 𝑥– 12 = 0
𝑥 = −1 𝑥 = 12
Hence, the value of 𝑥 is 12 since 𝑥 ∈ 𝑁.
(ii) 𝑥2– 4𝑥 – 12 = 0
By splitting the middle term,
𝑥2 + 2𝑥 − 6𝑥 – 12 = 0
𝑥(𝑥 + 2) − 6(𝑥 + 12) = 0
(𝑥 − 6)(𝑥 + 2) = 0
𝑥 − 6 = 0 𝑥 + 2 = 0
𝑥 = 6 𝑥 = −2
Hence, the value of 𝑥 is 6 and -2 since 𝑥 ∈ 𝐼
(iii) 2𝑥2 – 9𝑥 + 10 = 0
By splitting the middle term,
2𝑥2 – 4𝑥 − 5𝑥 + 10 = 0
2𝑥(𝑥 – 2) − 5(𝑥 − 2) = 0
(2𝑥 − 5)(𝑥 − 2) = 0
2𝑥 − 5 = 0 𝑥 − 2 = 0
𝑥 = 5/2 𝑥 = 2
Hence, the value of 𝑥 is 5/2 and 2 since 𝑥 ∈ 𝑄.
Question 15. Solve: (𝑎 + 𝑏)²𝑥² – (𝑎 + 𝑏)𝑥 – 6 = 0; 𝑎 + 𝑏 ≠ 0.
Solution:
It is given that,
(𝑎 + 𝑏)²𝑥² – (𝑎 + 𝑏)𝑥 – 6 = 0
By splitting the middle term,
(𝑎 + 𝑏)2𝑥2– 3(𝑎 + 𝑏)𝑥 + 2(𝑎 + 𝑏)𝑥 – 6 = 0
(𝑎 + 𝑏)𝑥[(𝑎 + 𝑏)𝑥– 3] + 2[(𝑎 + 𝑏)𝑥 – 3] = 0
[(𝑎 + 𝑏)𝑥 + 2][(𝑎 + 𝑏)𝑥 − 3] = 0
(𝑎 + 𝑏)𝑥 + 2 = 0 (𝑎 + 𝑏)𝑥 − 3 = 0
(𝑎 + 𝑏)𝑥 = −2 (𝑎 + 𝑏)𝑥 = 3
𝑥 = −2/(𝑎+𝑏) 𝑥 = 3/(𝑎+𝑏)
Question 16. Solve:

Question 17. Solve:
(i) 𝑥(𝑥 + 1) + (𝑥 + 2)(𝑥 + 3) = 42

Solution:
(i) 𝑥(𝑥 + 1) + (𝑥 + 2)(𝑥 + 3) = 42
𝑥2 + 𝑥 + 𝑥2 + 3𝑥 + 2𝑥 + 6 = 42
2𝑥2 + 6𝑥 + 6 − 42 = 0
2𝑥2 + 6𝑥 − 36 = 0
2𝑥2 + 12𝑥 − 6𝑥 − 36 = 0
2𝑥(𝑥 + 6) − 6(𝑥 + 6) = 0
(2𝑥 − 6)(𝑥 + 6) = 0
2𝑥 − 6 = 0 𝑥 + 6 = 0
𝑥 = 6/2 𝑥 = −6
𝑥 = 3

Question 18. For each equation, given below, find the value of 𝑚 so that the equation has equal roots.
Also, find the solution of each equation:
(i) (𝑚 − 3)𝑥2 − 4𝑥 + 1 = 0
(ii) 3𝑥2 + 12𝑥 + (𝑚 + 7) = 0
(iii) 𝑥2 − (𝑚 + 2)𝑥 + (𝑚 + 5) = 0
Solution:
(i) (𝑚 − 3)𝑥2 − 4𝑥 + 1 = 0
It is given that, the above equation equal roots so 𝐷 = 0
We know that,
𝐷 = 𝑏2 − 4𝑎𝑐
𝑏2 − 4𝑎𝑐 = 0
Here,
𝑎 = (𝑚 − 3)
𝑏 = −4
𝑐 = 1
Put the values,
(−4)2 − 4(𝑚 − 3)(1) = 0
16 − 4𝑚 + 12 = 0
−4𝑚 + 28 = 0
−4𝑚 = −28
𝑚 = 7
Put the value of 𝑚 in above equation,
(7 − 3)𝑥2 − 4𝑥 + 1 = 0
4𝑥2 − 4𝑥 + 1 = 0
4𝑥2 − 2𝑥 − 2𝑥 + 1 = 0
2𝑥(2𝑥 − 1) − 1(2𝑥 − 1) = 0
(2𝑥 − 1)(2𝑥 − 1) = 0
2𝑥 − 1 = 0
𝑥 = 1/2
Hence, the value of 𝑥 is 1/2.
(ii) 3𝑥2 + 12𝑥 + (𝑚 + 7) = 0
It is given that, the above equation equal roots so 𝐷 = 0
We know that,
𝐷 = 𝑏2 − 4𝑎𝑐
𝑏2 − 4𝑎𝑐 = 0
Here,
𝑎 = 3
𝑏 = 12
𝑐 = (𝑚 + 7)
Put the values,
(12)2 − 4(3)(𝑚 + 7) = 0
144 − 12(𝑚 + 7) = 0
144 − 12𝑚 − 84 = 0
−12𝑚 + 60 = 0
−12𝑚 = −60
𝑚 = 5
Put the value of 𝑚 in above equation,
3𝑥2 + 12𝑥 + (5 + 7) = 0
3𝑥2 + 12𝑥 + 12 = 0
3(𝑥2 + 4𝑥 + 4) = 0
𝑥2 + 4𝑥 + 4 = 0
𝑥2 + 2𝑥 + 2𝑥 + 4 = 0
𝑥(𝑥 + 2) + 2(𝑥 + 2) = 0
𝑥(𝑥 + 2) + 2(𝑥 + 2) = 0
𝑥 + 2 = 0
𝑥 = −2
Hence, the value of 𝑥 is −2.
(iii) 𝑥2 − (𝑚 + 2)𝑥 + (𝑚 + 5) = 0
It is given that, the above equation equal roots so 𝐷 = 0
We know that,
𝐷 = 𝑏2 − 4𝑎𝑐
𝑏2 − 4𝑎𝑐 = 0
Here,
𝑎 = 1
𝑏 = −(𝑚 + 2)
𝑐 = (𝑚 + 5)
Put the values,
[−(𝑚 + 2)]2 − 4(1)(𝑚 + 5) = 0
[𝑚2 + 2 × 𝑚 × (2) + 4]2 − 4(𝑚 + 5) = 0
𝑚2 + 4𝑚 + 4 − 4𝑚 − 20 = 0
𝑚2 − 16 = 0
𝑚2 = 16
𝑚 = ±4
Put the value of 𝑚 as 4 in above equation,
𝑥2 − (4 + 2)𝑥 + (4 + 5) = 0
𝑥2 − 6𝑥 + 9 = 0
𝑥2 − 3𝑥 − 3𝑥 + 9 = 0
𝑥(𝑥 − 3) − 3(𝑥 − 3) = 0
(𝑥 − 3)(𝑥 − 3) = 0
𝑥 − 3 = 0
𝑥 = 3
Put the value of 𝑚 as -4 in above equation,
𝑥2 − (−4 + 2)𝑥 + (−4 + 5) = 0
𝑥2 + 2𝑥 + 1 = 0
𝑥2 − 𝑥 − 𝑥 + 1 = 0
𝑥(𝑥 − 1) − 1(𝑥 − 1) = 0
(𝑥 − 1)(𝑥 − 1) = 0
𝑥 − 1 = 0
𝑥 = 1
Hence, the value of 𝑥 is 3 or 1.
Question 19. Without solving the following quadratic equation, find the value of p for which the roots are equal. 𝑝𝑥2 − 4𝑥 + 3 = 0
Solution:
It is given that, the above equation equal roots so 𝐷 = 0
We know that,
𝐷 = 𝑏2 − 4𝑎𝑐
𝑏2 − 4𝑎𝑐 = 0
𝑝𝑥2 − 4𝑥 + 3 = 0
Here,
𝑎 = 𝑝
𝑏 = −4
𝑐 = 3
Put the values,
(−4)2 − 4(𝑝)(3) = 0
16 − 12𝑝 = 0
−12𝑝 = −16
𝑝 = −16/−12
𝑝 = −16/−12
𝑝 = 4/3
Question 20. Without solving the following quadratic equation, find the value of ‘m’ for which the given
equation has real and equal roots.
𝑥² + 2(𝑚– 1)𝑥 + (𝑚 + 5) = 0
Solution:
It is given that, the above equation equal roots so 𝐷 = 0
We know that,
𝐷 = 𝑏2 − 4𝑎𝑐
𝑏2 − 4𝑎𝑐 = 0
𝑥² + 2(𝑚– 1)𝑥 + (𝑚 + 5) = 0
Here,
𝑎 = 1
𝑏 = 2(𝑚 − 1)
𝑐 = (𝑚 + 5)
Put the values,
[2(𝑚 − 1)]2 − 4(1)(𝑚 + 5) = 0
[4(𝑚2 − 2(𝑚)(1) + (1)2]2 − 4𝑚 − 20 = 0
4(𝑚2 − 2𝑚 + 1) − 4𝑚 − 20 = 0
4𝑚2 − 8𝑚 + 4 − 4𝑚 − 20 = 0
4𝑚2 − 12𝑚 − 16 = 0
4(𝑚2 − 3𝑚 − 4) = 0
𝑚2 − 3𝑚 − 4 = 0
𝑚2 − 4𝑚 + 𝑚 − 4 = 0
𝑚(𝑚 − 4) + 1(𝑚 − 4) = 0
(𝑚 + 1)(𝑚 − 4) = 0
𝑚 + 1 = 0 𝑚 − 4 = 0
𝑚 = −1 𝑚 = 4
Hence, the value of m is -1 and 4.
Exercise 5F
Question 1. Solve:
(i) (𝑥 + 5)(𝑥– 5) = 24
(ii) 3𝑥2 − 2√6𝑥 + 2 = 0
(ii) 3√2𝑥2 − 5𝑥 + √26 = 0
Solution:
(i) (𝑥 + 5)(𝑥 – 5) = 24
𝑥2 – (5)2 = 24
We know that,
(𝑎 – 𝑏)(𝑎 + 𝑏) = 𝑎2– 𝑏2
𝑥2– 25 = 24
𝑥2 = 49
𝑥 = ± 7
(ii) 3𝑥2 – 2√6𝑥 + 2 = 0
3𝑥2– √6𝑥– √6𝑥 + 2 = 0
√3𝑥(√3𝑥– √2)– √2(√3𝑥 − √2) = 0
(√3𝑥– √2)(√3𝑥 − √2) = 0
(√3𝑥– √2)(√3𝑥 − √2) = 0
√3𝑥– √2 = 0
𝑥 = √2/√3
(iii) 3√2𝑥2 − 5𝑥 − √2 = 0
3√2𝑥2 − 6𝑥 + 𝑥 − √2 = 0
3√2𝑥(𝑥 − √2) + 1(𝑥 − √2) = 0
(3√2𝑥 + 1)(𝑥 − √2) = 0
3√2𝑥 + 1 = 0 𝑥 − √2 = 0
3√2𝑥 = −1 𝑥 = √2
𝑥 = − 1/3√2
Question 2. One root of the quadratic equation 8𝑥2 + 𝑚𝑥 + 15 is 3/4. Find the value of m. Also, find the other root of the equation.
Solution:
It is given that,
The one root of equation is 3/4.
Quadratic equation is 8𝑥2 + 𝑚𝑥 + 15 = 0
Put the value of 𝑥 as 3/4 in given equation,

Put the value of 𝑚 in given equation,
8𝑥2 + 𝑚𝑥 + 15 = 0
8𝑥2 + (−26)𝑥 + 15 = 0
8𝑥2 − 26𝑥 + 15 = 0
8𝑥2 − 20𝑥 − 6𝑥 + 15 = 0
4𝑥(2𝑥 − 5) − 3(2𝑥 − 5) = 0
(4𝑥 − 3)(2𝑥 − 5) = 0
4𝑥 − 3 = 0 2𝑥 − 5 = 0
𝑥 = 3/4 𝑥 = 5/2
Hence, the other root of given equation is 5/2.
Question 3. One root of the quadratic equation 𝑥2 – 3𝑥– 2𝑎𝑥 – 6𝑎 = 0 is −3, find its other root.
Solution:
It is given that,
The one root of equation is −3.
Quadratic equation is 𝑥2 – 3𝑥– 2𝑎𝑥 – 6𝑎 = 0
Put the value of 𝑥 as −3 in given equation,
𝑥2 – 3𝑥 – 2𝑎𝑥 – 6𝑎 = 0
𝑥(𝑥 + 3) – 2𝑎(𝑥 + 3) = 0
(𝑥– 2𝑎)(𝑥 + 3) = 0
𝑥 − 2𝑎 = 0 𝑥 + 3 = 0
𝑥 = 2𝑎 𝑥 = −3
Hence, the other root of the given equation is 2a.
Question 4. If 𝑝– 15 = 0 and 2𝑥2 + 15𝑥 + 15 = 0; find the values of 𝑥.
Solution:
It is given that,
𝑝– 15 = 0
𝑝 = 15
Put the value of 𝑝 in given equation,
2𝑥2 + 15𝑥 + 15 = 0
2𝑥 + 10𝑥 + 5𝑥 + 15 = 0
2𝑥(𝑥 + 5) + 5(𝑥 + 5)
(2𝑥 + 5)(𝑥 + 5) = 0
2𝑥 + 5 = 0 𝑥 + 5 = 0
𝑥 = −5/2 𝑥 = −5
Hence, the value of 𝑥 is −5/2 and -5.
Question 5. Find the solution of the equation 2𝑥2 − 𝑚𝑥 – 25𝑛 = 0; if 𝑚 + 5 = 0 and 𝑛 – 1 = 0.
Solution:
It is given that,
𝑚 + 5 = 0
𝑚 = −5
And
𝑛 – 1 = 0
𝑛 = 1
Put the value of 𝑚 and 𝑛 in given equation
2𝑥2 − 𝑚𝑥 – 25𝑛 = 0
2𝑥2 − (−5)𝑥 – 25(1) = 0
2𝑥2 + 5𝑥 – 25 = 0
2𝑥 + 10𝑥– 5𝑥– 25 = 0
2𝑥(𝑥 + 5) − 5(𝑥 + 5) = 0
(𝑥 + 5)(2𝑥– 5) = 0
𝑥 + 5 = 0 2𝑥 − 5 = 0
𝑥 = −5 𝑥 = 5/2
Hence, the value of 𝑥 is -5 and 5/2.𝑥2
Question 6. If m and n are roots of the equation (1/𝑥) − (1/𝑥−2) = 3 where 𝑥 ≠ 0 and 𝑥 ≠ 2; find 𝑚 × 𝑛.
Solution:


Question 7. Solve, using formula: 𝑥2 + 𝑥 – (𝑎 + 2)(𝑎 + 1) = 0
Solution:
It is given that,
𝑥2 + 𝑥 – (𝑎 + 2)(𝑎 + 1) = 0
By the quadratic formula
𝑎 = 1
𝑏 = 1
𝑐 = – (𝑎 + 2)(𝑎 + 1)

Question 8. Solve the quadratic equation 8𝑥2– 14𝑥 + 3 = 0
(i) When 𝑥 ∈ 𝐼 (integers)
(ii) When 𝑥 ∈ 𝑄 (rational numbers)
Solution:
It is given that,
8𝑥2– 14𝑥 + 3 = 0
8𝑥2– 12𝑥 − 2𝑥 + 3 = 0
4𝑥(2𝑥 – 3) – (2𝑥– 3) = 0
(4𝑥– 1)(2𝑥– 3) = 0
4𝑥 − 1 = 0 2𝑥 − 3 = 0
𝑥 = 1/4 𝑥 = 3/2
(i) When 𝑥 ∈ 𝐼 (integers) the given 8𝑥2– 14𝑥 + 3 = 0 has no equal roots.
(ii) When 𝑥 ∈ 𝑄 (rational numbers) the given 8𝑥2– 14𝑥 + 3 = 0 are 𝑥 = 1/4 , 3/2
.
Question 9. Find the value of m for which the equation (𝑚 + 4 )2 + (𝑚 + 1)𝑥 + 1 = 0 has real and equal roots.
Solution:
Given quadratic equation is (m + 4 )2 + (m + 1)x + 1 = 0
The quadratic equation has real and equal roots if its discriminant is zero.
⇒ D = 𝑏2 – 4ac = 0
⇒ (m + 1)2 -4(m + 4)(1) = 0
⇒ m2 + 2m + 1 – 4m – 16 = 0
⇒ m2 – 2m – 15 = 0
⇒ m2 – 5m + 3m – 15 = 0
⇒ m(m – 5) +3(m =5) = 0
⇒ (m – 5)(m + 3) = 0
⇒ m = 5 or m = -3
Question 10. Find the values of m for which equation 3𝑥2 + m𝑥 + 2 = 0 has equal roots. Also, find the roots of the given equation.
Solution:
It is given that, the above equation equal roots so 𝐷 = 0
We know that,
𝐷 = 𝑏2 − 4𝑎𝑐
𝑏2 − 4𝑎𝑐 = 0
3𝑥² + 𝑚𝑥 + 2 = 0
Here,
𝑎 = 3
𝑏 = 𝑚
𝑐 = 2
Put the values,
m2 − 4(2)(3) = 0
m2 − 24 = 0
m2 = 24
𝑚 = √24
𝑚 = ±2√6
Put the value of 𝑚 as 2√6 in given equation,
3𝑥² + 2√6𝑥 + 2 = 0
(√3𝑥)² + 2(√3𝑥)(√2) + (√2)2 = 0
(√3𝑥 + √2)² = 0
√3𝑥 + √2 = 0
√3𝑥 = −√2

Question 11. Find the value of k for which equation 4𝑥2 + 8𝑥 – 𝑘 = 0 has real roots.
Solution:
It is given that, the above equation equal roots so 𝐷 ≥ 0
We know that,
𝐷 = 𝑏2 − 4𝑎𝑐
𝑏2 − 4𝑎𝑐 ≥ 0
4𝑥² + 8𝑥 − 𝑘 ≥ 0
Here,
𝑎 = 4
𝑏 = 8
𝑐 = −𝑘
Put the values,
(8)2 − 4(4)(−𝑘) ≥ 0
64 + 16𝑘 ≥ 0
16𝑘 ≥ −64
𝑘 ≥ −64/16
𝑘 ≥ −4
Hence, the value of 𝑘 is −4 when given equation has real roots.
Question 12. Find, using quadratic formula, the roots of the following quadratic equations, if they exist
(𝑖) 3𝑥2 – 5𝑥 + 2 = 0
(𝑖𝑖) 𝑥2 + 4𝑥 + 5 = 0
Solution:
(i) 3𝑥2 – 5𝑥 + 2 = 0
Here,
𝑎 = 3
𝑏 = −5
𝑐 = 2
Put the values,
𝐷 = 𝑏2 − 4𝑎𝑐
𝐷 = (−5)2 – 4(3)(2)
𝐷 = 25 – 24
𝐷 = 1
We know that,
𝐷 > 0, so the roots of the quadratic equation are real and distinct.
By quadratic formula

(ii) 𝑥2 + 4𝑥 + 5 = 0
Here,
𝑎 = 1
𝑏 = 4
𝑐 = 5
Put the values,
𝐷 = 𝑏2 − 4𝑎𝑐
𝐷 = (4)2 − 4(1)(5)
𝐷 = 16 − 20
𝐷 = −4
Hence, 𝐷 > 0, so the roots of the quadratic equation does not exist.
Question 13. Solve:

48𝑥 = 324– 𝑥2
𝑥2 + 48𝑥 − 324 =
𝑥2 + 48𝑥 – 324 = 0
𝑥2 + 54𝑥 – 6𝑥 – 324 = 0
𝑥(𝑥 + 54) − 6(𝑥 + 54) = 0
(𝑥 + 54)(𝑥 – 6) = 0
𝑥 = −54 𝑜𝑟 𝑥 = 6
Hence, the value of 𝑥 > 0.





