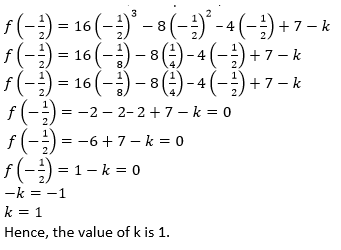Question 1. Find in each case the remainder when:
(i) 𝑥4 − 3𝑥2 + 2𝑥 + 1 is divided by 𝑥 − 1.
(ii) 𝑥3 − 3𝑥2 − 12𝑥 + 4 is divided by 𝑥 − 2.
(iii) 𝑥4 + 1 is divided by 𝑥 + 1.
Solution:
(i) 𝑥4 − 3𝑥2 + 2𝑥 + 1 is divided by 𝑥 − 1.
𝑥 − 1 = 0
𝑥 = 1
Put the value of x in given equation.
𝑥4 − 3𝑥2 + 2𝑥 + 1
(1)4 − 3(1)2 + 2(1) + 1
1 − 3(1) + 2 + 1
1 − 3 + 2 + 1
4 − 3 = 1
Hence, the reminder is 1.
(ii) 𝑥3 − 3𝑥2 − 12𝑥 + 4 is divided by x − 2.
𝑥 − 2 = 0
𝑥 = 2
Put the value of x in given equation.
𝑥3 − 3𝑥2 − 12𝑥 + 4
(2)3 + 3(2)2 − 12(2) + 4
8 + 3(4) − 24 + 4
8 + 12 − 24 + 4
24 − 24 = 0
Hence, the reminder is 0.
(iii) 𝑥4 + 1 is divided by 𝑥 + 1.
𝑥 + 1 = 0
𝑥 = −1
Put the value of x in given equation.
𝑥4 + 1
(−1)4 + 1
1 + 1 = 2
Hence, the reminder is 2.
Question 2. Show that:
(i) 𝑥 − 2 is a factor of 5𝑥2 + 15𝑥 − 50.
(ii) 3𝑥 + 2 is a factor of 3𝑥2 − 𝑥 − 2.
Solution:
(i) It is given that,
𝑥 − 2 is the factor of 5𝑥2 + 15𝑥 − 50
So,
𝑥 − 2 = 0
𝑥 = 2
Put the value of 𝑥 in given equation,
𝑓(𝑥) = 5𝑥2 + 15𝑥 − 50
𝑓(2) = 5(2)2 + 15(2) − 50
𝑓(2) = 5 × 4 + 30 − 50
𝑓(2) = 20 + 30 − 50
𝑓(2) = 50 − 50
𝑓(2) = 0
Hence, it is proved that 𝑥 − 2 is a factor of 5𝑥2 + 15𝑥 − 50.
(ii) It is given that,
3𝑥 + 2 is the factor of 3𝑥2 − 𝑥 − 2
So,
3𝑥 + 2 = 0
𝑥 = −2/3
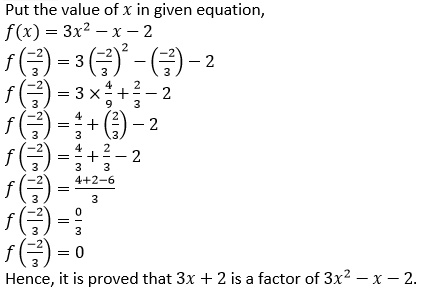
Question 3. Use the Remainder Theorem to find which of the following is a factor of 2𝑥3 + 3𝑥2– 5𝑥– 6.
(i) 𝑥 + 1
(ii) 2𝑥– 1
(iii) 𝑥 + 2
Solution:
(i) It is given that,
𝑥 + 1 is the factor of 2𝑥3 + 3𝑥2– 5𝑥– 6
𝑥 + 1 = 0
𝑥 = −1
Put the value of 𝑥 in given equation,
𝑓(𝑥) = 2𝑥3 + 3𝑥2– 5𝑥– 6
𝑓(−1) = 2(−1)3 + 3(−1)2 − 5(−1) − 6
𝑓(−1) = 2 × −1 + 3 × 1 − 5 × (−1) − 6
𝑓(−1) = −2 + 3 + 5 − 6
𝑓(−1) = −8 + 8
𝑓(−1) = 0
Hence, it is proved that 𝑥 + 1 is a factor of 2𝑥3 + 3𝑥2– 5𝑥– 6.
(ii) It is given that,
2𝑥 − 1 is the factor of 2𝑥3 + 3𝑥2– 5𝑥– 6
2𝑥 − 1 = 0
𝑥 = 1/2
(iii) It is given that,
𝑥 + 2 is the factor of 2𝑥3 + 3𝑥2– 5𝑥– 6
𝑥 + 2 = 0
𝑥 = −2
Put the value of 𝑥 in given equation,
𝑓(𝑥) = 2𝑥3 + 3𝑥2– 5𝑥– 6
𝑓 (−2) = 2(−2)3 + 3(−2)2– 5(−2)– 6
𝑓 (−2) = −16 + 12 + 10– 6
𝑓 (−2) = 0
Thus, (x + 2) is a factor of the polynomial f(x).
Question 4. (i) If 2𝑥 + 1 is a factor of 2𝑥2 + 𝑎𝑥– 3, find the value of a.
(ii) Find the value of k, if 3𝑥– 4 is a factor of expression 3𝑥2 + 2𝑥– 𝑘.
Solution:
(i) It is given that,
2𝑥 + 1 is a factor of 2𝑥2 + 𝑎𝑥– 3
So,
2𝑥2 + 𝑎𝑥– 3 = 0
We know that,
2𝑥 + 1 = 0
2𝑥 = −1
𝑥 = − 1/2
Put the value of 𝑥 in above equation,
2𝑥2 + 𝑎𝑥– 3 = 0
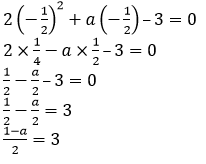
1 − 𝑎 = 3 × 2
1 − 𝑎 = 6
−𝑎 = 6 − 1
−𝑎 = 5
𝑎 = −5
Hence, the value of 𝑎 is −5.
(ii) It is given that,
3𝑥 − 4 is a factor of 3𝑥2 + 2𝑥– 𝑘
So,
3𝑥2 + 2𝑥– 𝑘 = 0
We know that,
3𝑥 − 4 = 0
3𝑥 = 4
𝑥 = 4/3
Put the value of 𝑥 in above equation,
3𝑥2 + 2𝑥– 𝑘 = 0
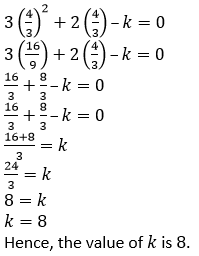
Question 5. Find the values of constants a and b when 𝑥– 2 and 𝑥 + 3 both are the factors of expression 𝑥3 + 𝑎𝑥2 + 𝑏𝑥– 12.
Solution:
It is given that,
𝑓(𝑥) = 𝑥 + 𝑎𝑥2 + 𝑏𝑥– 12
𝑥 − 2 is the factor of 𝑥 + 𝑎𝑥2 + 𝑏𝑥– 12
𝑥 − 2 = 0
𝑥 = 2
Put the value of 𝑥 in given equation,
(2)3 + 𝑎(2)2 + 𝑏(2)– 12 = 0
8 + 4𝑎 + 2𝑏– 12 = 0
4𝑎 + 2𝑏– 4 = 0
2(2𝑎 + 𝑏– 2) = 0
2𝑎 + 𝑏– 2 = 0
2𝑎 + 𝑏 = 2 _(1)
𝑥 + 3 is the factor of 𝑥 + 𝑎𝑥2 + 𝑏𝑥– 12
𝑥 + 3 = 0
𝑥 = −3
Put the value of 𝑥 in given equation,
(−3)3 + 𝑎(−3)2 + 𝑏(−3)– 12 = 0
−27 + 𝑎 × 9 − 𝑏 × 3– 12 = 0
−27 + 9𝑎 − 3𝑏– 12 = 0
9𝑎 − 3𝑏– 39 = 0
3(3𝑎 − 𝑏– 13) = 0
3𝑎 − 𝑏– 13 = 0
3𝑎 − 𝑏 = 13_____________(2)
From equation 1 we get,
2𝑎 + 𝑏 = 2
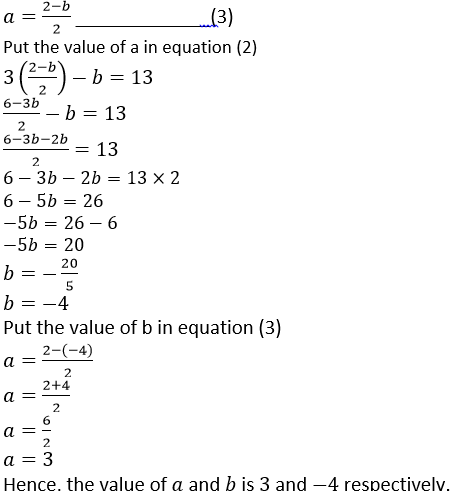
Question 6. Find the value of k, if 2𝑥 + 1 is a factor of (3𝑘 + 2)𝑥3 + (𝑘– 1).
Solution:
It is given that,
2𝑥 + 1 is a factor of (3𝑘 + 2)𝑥3 + (𝑘– 1)
2𝑥 + 1 = 0
𝑥 = − 1/2
Put the value of 𝑥 in given equation,
(3𝑘 + 2)𝑥3+ (𝑘– 1) = 0
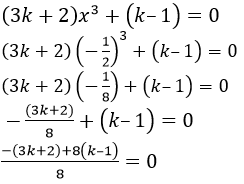
−3𝑘 − 2 + 8𝑘– 8 = 0
5𝑘– 10 = 0
5𝑘 = 10
𝑘 = 10/5
𝑘 = 2
Hence, the value of 𝑘 is 2.
Question 7. Find the value of a, if 𝑥– 2 is a factor of 2𝑥5– 6𝑥4– 2𝑎𝑥3 + 6𝑎𝑥2 + 4𝑎𝑥 + 8.
Solution:
It is given that,
𝑓(𝑥) = 2𝑥5– 6𝑥4– 2𝑎𝑥3 + 6𝑎𝑥2 + 4𝑎𝑥 + 8 = 0
𝑥– 2 is a factor of 2𝑥5– 6𝑥4– 2𝑎𝑥3 + 6𝑎𝑥2 + 4𝑎𝑥 + 8
𝑥– 2 = 0
𝑥 = 2
Put the value of 𝑥 in given equation,
2(2)5 – 6(2)4 – 2𝑎(2)3 + 6𝑎(2)2 + 4𝑎(2) + 8 = 0
2(32) – 6(16) – 2𝑎(8) + 6𝑎(4) + 4𝑎(2) + 8 = 0
64– 96– 16𝑎 + 24𝑎 + 8𝑎 + 8 = 0
−24 + 16𝑎 = 0
16𝑎 = 24
𝑎 = 1.5
Hence, the value of 𝑎 is 1.5.
Question 8. Find the values of m and n so that 𝑥– 1 and 𝑥 + 2 both are factors of 𝑥3 + (3𝑚 + 1)𝑥2 + 𝑛𝑥–18.
Solution:
It is given that,
𝑓(𝑥) = 𝑥3 + (3𝑚 + 1)𝑥2 + 𝑛𝑥 − 18
𝑥– 1 is a factor of 𝑥3 + (3𝑚 + 1)𝑥2 + 𝑛𝑥 − 18
𝑥– 1 = 0
𝑥 = 1
Put the value of 𝑥 in given equation,
𝑥3 + (3𝑚 + 1)𝑥2 + 𝑛𝑥 − 18 = 0
(1)3 + (3𝑚 + 1)(1)2 + 𝑛(1) − 18 = 0
1 + (3𝑚 + 1)1 + 𝑛 − 18 = 0
1 + 3𝑚 + 1 + 𝑛 − 18 = 0
3𝑚 + 𝑛 − 16 = 0____________(1)
𝑥 + 2 is a factor of 𝑥3 + (3𝑚 + 1)𝑥2 + 𝑛𝑥 − 18
𝑥 + 2 = 0
𝑥 = −2
Put the value of 𝑥 in given equation,
(−2)3 + (3𝑚 + 1)(−2)2 + 𝑛(−2) − 18 = 0
−8 + (3𝑚 + 1)(4) − 2𝑛 − 18 = 0
−8 + 12𝑚 + 4 − 2𝑛 − 18 = 0
12𝑚 − 2𝑛 − 22 = 0
6𝑚 − 𝑛 − 11 = 0____________(2)
From equation (1) we get, the value of 𝑚
3𝑚 + 𝑛 − 16 = 0
𝑚 = 16−𝑛 /3 _(3)
Put the value of 𝑚 in equation (2)
6 (16−𝑛/3 ) − 𝑛 − 11 = 0
2(16 − 𝑛) − 𝑛 − 11 = 0
32 − 2𝑛 − 𝑛 − 11 = 0
21 − 3𝑛 = 0
−3𝑛 = −21
𝑛 = −21/−3
𝑛 = 7
Put the value of 𝑛 in equation (3)
𝑚 = 16−7/3
𝑚 = 9/3
𝑚 = 3
Hence, the value of 𝑚 is 3 and 𝑛 is 7.
Question 9. When 𝑥3 + 2𝑥2– 𝑘𝑥 + 4 is divided by 𝑥– 2, the remainder is k. Find the value of constant k.
Solution:
It is given that,
𝑓(𝑥) = 𝑥3 + 2𝑥2 + 𝑘𝑥 + 4 = 0
𝑥 − 2 is a factor of 𝑥3 + 2𝑥2 − 𝑘𝑥 + 4
𝑥 − 2 = 0
𝑥 = 2
Put the value of 𝑥 in given equation,
𝑥3 + 2𝑥2 − 𝑘𝑥 + 4 = 𝑘
(2)3 + 2(2)2 − 𝑘(2) + 4 = 𝑘
8 + 2 × 4 − 𝑘(2) + 4 = 𝑘
8 + 8 − 2𝑘 + 4 = 𝑘
20 − 2𝑘 = 𝑘
20 = 𝑘 + 2𝑘
20 = 3𝑘
𝑘 = 20/3
𝑘 = 6 (2/3)
Hence, the value of k is 6 (2/3).
Question 10. Find the value of 𝑎, if the division of 𝑎𝑥3 + 9𝑥2 + 4𝑥– 10 by 𝑥 + 3 leaves a remainder 5.
Solution:
It is given that,
𝑓(𝑥) = 𝑎𝑥3 + 9𝑥2 + 4𝑥 − 10 = 5
𝑥 + 3 is a factor of 𝑥3 + 2𝑥2 − 𝑘𝑥 + 4
𝑥 + 3 = 0
𝑥 = −3
Put the value of 𝑥 in given equation,
𝑎𝑥3 + 9𝑥2 + 4𝑥 − 10 = 5
𝑎(−3)3 + 29 + 4(−3) − 10 = 5
−27𝑎 + 9 × 9 − 12 − 10 = 5
−27𝑎 + 81 − 12 − 10 = 5
−27𝑎 + 54 = 0
−27𝑎 = −54
𝑎 = −54/−27
𝑎 = 2
Hence, the value of 𝑎 is 2.
Question 11. If 𝑥3 + 𝑎𝑥2 + 𝑏𝑥 + 6 has 𝑥– 2 as a factor and leaves a remainder 3 when divided by 𝑥– 3, find the values of a and b.
Solution:
It is given that,
𝑓(𝑥) = 𝑥3 + 𝑎𝑥2 + 𝑏𝑥 + 6 = 0
𝑥 + 2 is a factor of 𝑥3 + 𝑎𝑥2 + 𝑏𝑥 + 6
𝑥 + 2 = 0
𝑥 = −2
Put the value of 𝑥 in given equation,
(2)3 + 𝑎(2)2 + 𝑏(2) + 6 = 0
8 + 𝑎(4) + 𝑏(2) + 6 = 0
8 + 4𝑎 + 2𝑏 + 6 = 0
4𝑎 + 2𝑏 + 14 = 0
2(2𝑎 + 𝑏 + 7) = 0
2𝑎 + 𝑏 + 7 = 0 _(1)
𝑥 − 3 is a factor of 𝑥3 + 𝑎𝑥2 + 𝑏𝑥 + 6 = 3
𝑥 − 3 = 0
𝑥 = 3
Put the value of 𝑥 in given equation,
(3)3 + 𝑎(3)2 + 𝑏(3) + 6 = 3
27 + 𝑎(9) + 𝑏(3) + 6 = 3
27 + 9𝑎 + 3𝑏 + 6 = 3
9𝑎 + 3𝑏 + 33 − 3 = 0
9𝑎 + 3𝑏 + 30 = 0
3(3𝑎 + 𝑏 + 10) = 0
3𝑎 + 𝑏 + 10 = 0 _(2)
From equation (1) we get,
2𝑎 + 𝑏 + 7 = 0
𝑏 = −7 − 2𝑎 __(3)
Put the value of b in equation (2)
3𝑎 + (−7 − 2𝑎) + 10 = 0
3𝑎 − 7 − 2𝑎 + 10 = 0
3𝑎 − 2𝑎 + 3 = 0
𝑎 = −3
Put the value of a in equation (3)
𝑏 = −7 − 2(−3)
𝑏 = −7 + 6
𝑏 = −1
Hence, the value of a is -3 and value of b is -1.
Question 12. The expression 2𝑥3 + 𝑎𝑥2 + 𝑏𝑥– 2 leaves remainder 7 and 0 when divided by 2𝑥– 3 and 𝑥 + 2 respectively. Calculate the values of a and b.
Solution:
It is given that,
𝑓(𝑥) = 2𝑥3 + 𝑎𝑥2 + 𝑏𝑥 − 2 = 0
2𝑥 − 3 is a factor of 2𝑥3 + 𝑎𝑥2 + 𝑏𝑥 − 2
2𝑥 − 3 = 0
𝑥 = 3/2
Put the value of 𝑥 in given equation,
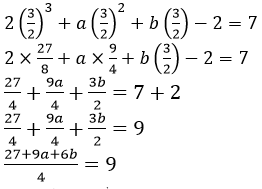
27 + 9𝑎 + 6𝑏 = 9 × 4
27 + 9𝑎 + 6𝑏 = 36
9𝑎 + 6𝑏 = 36 − 27
9𝑎 + 6𝑏 = 9
3(3𝑎 + 2𝑏) = 9
3𝑎 + 2𝑏 = 9/3
3𝑎 + 2𝑏 = 3__________(1)
𝑥 + 2 is a factor of 2𝑥3 + 𝑎𝑥2 + 𝑏𝑥 − 2 = 0
𝑥 + 2 = 0
𝑥 = −2
Put the value of 𝑥 in given equation,
2(−2)3 + 𝑎(−2)2 + 𝑏(−2) − 2 = 0
2 × (−8) + 𝑎(4)2 + 𝑏(−2) − 2 = 0
−16 + 4𝑎 − 2𝑏 − 2 = 0
4𝑎 − 2𝑏 − 18 = 0 _(2)
From equation (1) we get,
3𝑎 + 2𝑏 = 3
𝑎 = 3−2𝑏/3 ___(3)
Put the value of a in equation (2)
4𝑎 − 2𝑏 − 18 = 0
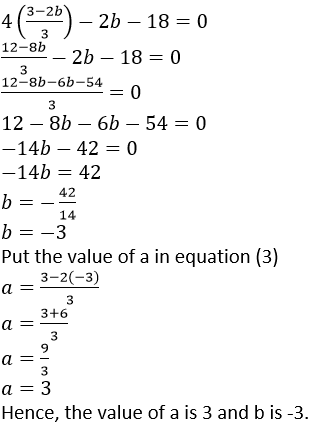
Question 13. What number should be added to 3𝑥3 − 5𝑥2 + 6𝑥 so that when resulting polynomial is divided by 𝑥– 3, the remainder is 8?
Solution:
Let us assumed that,
𝐾 is added to given polynomial
So, the polynomial is,
𝑓(𝑥) = 3𝑥3 − 5𝑥2 + 6𝑥 + 𝑘
𝑥 − 3 is a factor of 3𝑥3 − 5𝑥2 + 6𝑥 + 𝑘 and remainder is 8.
𝑥 − 3 = 0
𝑥 = 3
Put the value of 𝑥 in given equation,
3𝑥3 − 5𝑥2 + 6𝑥 + 𝑘 = 8
3(3)3 − 5(3)2 + 6(3) + 𝑘 = 8
3(27) − 5(9) + 6(3) + 𝑘 = 8
81 − 45 + 18 + 𝑘 = 8
54 + 𝑘 = 8
𝑘 = 8 − 54
𝑘 = −46
Hence, the value of k is -46.
Question 14. What number should be subtracted from 𝑥3 + 3𝑥2– 8𝑥 + 14 so that on dividing it with 𝑥– 2, the remainder is 10.
Solution:
Let us assumed that,
𝑘 is subtracted to given polynomial
So, the polynomial is,
𝑓(𝑥) = 𝑥3 + 3𝑥2 − 8𝑥 + 14 − 𝑘
𝑥 − 2 is a factor of 𝑥3 + 3𝑥2 − 8𝑥 + 14 and remainder is 10.
𝑥 − 2 = 0
𝑥 = 2
Put the value of 𝑥 in given equation,
𝑥3 + 3𝑥2 − 8𝑥 + 14 − 𝑘 = 10
(2)3 + 3(2)2 − 8(2) + 14 − 𝑘 = 10
8 + 3(4) − 8(2) + 14 − 𝑘 = 10
8 + 12 − 16 + 14 − 𝑘 = 10
18 − 𝑘 = 10
−𝑘 = 10 − 18
−𝑘 = −8
𝑘 = 8
Hence, the value of k is 8.
Question 15. The polynomials 2𝑥3– 7𝑥2 + 𝑎𝑥– 6 and 𝑥3– 8𝑥2 + (2𝑎 + 1)𝑥– 16 leaves the same remainder when divided by 𝑥– 2. Find the value of ‘a’.
Solution:
It is given that,
𝑓(𝑥) = 2𝑥3– 7𝑥2 + 𝑎𝑥– 6
𝑥 − 2 is a factor of 2𝑥3– 7𝑥2 + 𝑎𝑥 − 6
𝑥 − 2 = 0
𝑥 = 2
Put the value of 𝑥 in given equation,
𝑓(2) = 2(2)3– 7(2)2 + 𝑎(2)– 6
𝑓(2) = 2(8)– 7(4) + 𝑎(2)– 6
𝑓(2) = 16– 28 + 2𝑎– 6
𝑓(2) = 2𝑎– 18
Again,
𝑔(𝑥) = 𝑥3– 8𝑥2 + (2𝑎 + 1)𝑥– 16
𝑥 − 2 is a factor of 𝑥3– 8𝑥2 + (2𝑎 + 1)𝑥 − 16
𝑥 − 2 = 0
𝑥 = 2
Put the value of 𝑥 in given equation,
𝑔(2) = (2)3 − 8(2)2 + (2𝑎 + 1)(2) − 16
𝑔(2) = 8 − 8(4) + 4𝑎 + 2 − 16
𝑔(2) = 8 − 32 + 4𝑎 + 2 − 16
𝑔(2) = 4𝑎 − 38
It is given that,
Polynomial leaves the same remainder
𝑓(2) = 𝑔(2)
2𝑎– 18 = 4𝑎 − 38
2𝑎 − 4𝑎 = −38 + 18
−2𝑎 = −20
𝑎 = 20/2
𝑎 = 10
Hence, the value of a is 10.
Question 16. If (𝑥– 2) is a factor of the expression 2𝑥3 + 𝑎𝑥2 + 𝑏𝑥– 14 and when the expression is divided by (𝑥– 3), it leaves a remainder 52, find the values of a and b.
Solution:
It is given that,
𝑓(𝑥) = 2𝑥3 + 𝑎𝑥2 + 𝑏𝑥– 14
𝑥 − 2 is a factor of 2𝑥3 + 𝑎𝑥2 + 𝑏𝑥– 14
𝑥 − 2 = 0
𝑥 = 2
2(2)3 + 𝑎(2)2 + 𝑏(2)– 14 = 0
16 + 4𝑎 + 2𝑏– 14 = 0
4𝑎 + 2𝑏 + 2 = 0
2𝑎 + 𝑏 + 1 = 0
2𝑎 + 𝑏 = −1_________(𝑖)
(𝑥 − 3) is a factor of 2𝑥3 + 𝑎𝑥2 + 𝑏𝑥– 14 and remainder is 52,
2(3)3 + 𝑎(3)2 + 𝑏(3)– 14 = 52
54 + 9𝑎 + 3𝑏– 14 = 52
9𝑎 + 3𝑏 + 40 = 52
9𝑎 + 3𝑏 = 12
3𝑎 + 𝑏 = 4___________(𝑖𝑖)
From equation (1) we get the value of a,
2𝑎 + 𝑏 = −1
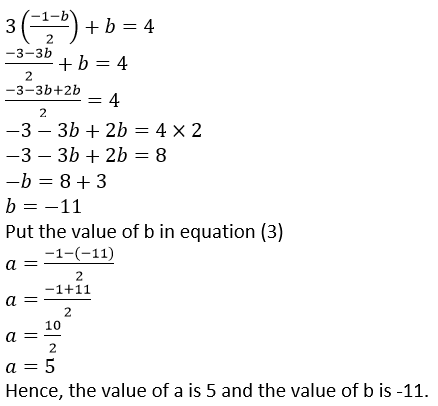
Question 17. Find ‘a’ if the two polynomials 𝑎𝑥3 + 3𝑥2– 9 and 2𝑥3 + 4𝑥 + 𝑎, leave the same remainder when divided by 𝑥 + 3.
Solution:
It is given that,
Two polynomial have same remainder.
𝑥 + 3 = 0
𝑥 = −3
Value of polynomial 𝑎𝑥3 + 3𝑥2– 9 at 𝑥 = −3 is same as value of polynomial 2𝑥3 + 4𝑥 + 𝑎 𝑎𝑡 𝑥 = −3
𝑎(−3)3 + 3(−3)2 – 9 = 2(−3)3 + 4(−3) + 𝑎
−27𝑎 + 27 – 9 = −54 – 12 + 𝑎
−27𝑎 + 18 = −66 + 𝑎
−27𝑎 − 𝑎 = −66 − 18
−28𝑎 = −84
𝑎 = −84/−28
𝑎 = 3
Hence, the value of a is 3.
Exercise 8B
Question 1. Using the Factor Theorem, show that:
(i) (𝑥– 2) is a factor of 𝑥3– 2𝑥2– 9𝑥 + 18.
Hence, factories the expression 𝑥3– 2𝑥2– 9𝑥 + 18 completely.
(ii) (𝑥 + 5) is a factor of 2𝑥3 + 5𝑥2 – 28𝑥– 15.
Hence, factories the expression 2𝑥3 + 5𝑥2 – 28𝑥– 15 completely.
(iii) (3𝑥 + 2) is a factor of 3𝑥3 + 2𝑥2– 3𝑥– 2.
Hence, factories the expression 3𝑥3 + 2𝑥2– 3𝑥– 2 completely.
Solution:
(i) It is given that,
(𝑥– 2) is a factor of 𝑥3– 2𝑥2 – 9𝑥 + 18
𝑥 − 2 = 0
𝑥 = 2
Put the value of 𝑥 in given equation,
𝑓(2) = (2)3– 2(2)2 + 9(2) + 18
𝑓(2) = (8)– 2(4) + 9(2) + 18
𝑓(2) = 8– 8 + 18 + 18
𝑓(2) = 0
Now,
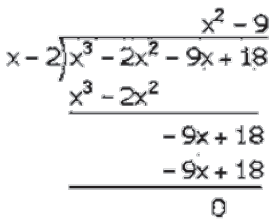
Factorization of 𝑥3– 2𝑥2– 9𝑥 + 18 is
(𝑥 − 2)(𝑥2 − 9)
(𝑥 − 2)(𝑥2 − (3)2)
(𝑥 − 2)(𝑥 − 3)(𝑥 + 3)
Hence, the factors of 𝑥3– 2𝑥2– 9𝑥 + 18 is (𝑥 − 2)(𝑥 − 3)(𝑥 + 3).
(ii) It is given that,
(𝑥 + 5) is a factor of 2𝑥3 + 5𝑥2 – 28𝑥– 15
𝑥 + 5 = 0
𝑥 = −5
Put the value of 𝑥 in given equation,
𝑓(−5) = 2(−5)3 + 5(−5)2 + 28(−5) − 15
𝑓(−5) = 2(−125) + 5(25) + 28(−5) − 15
𝑓(−5) = −250 + 125 + 140 − 15
𝑓(−5) = −265 + 265
𝑓(−5) = 0
Now,
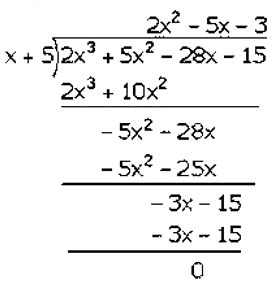
Factorization of 2𝑥3 + 5𝑥2– 28𝑥 − 15 is
(𝑥 + 5)(2𝑥2 − 5𝑥 − 3)
(𝑥 + 5)(2𝑥2 − 6𝑥 + 𝑥 − 3)
(𝑥 + 5)[2𝑥(𝑥 − 3) + 1(𝑥 − 3)]
(𝑥 + 5)(2𝑥 + 1)(𝑥 − 3)
Hence, the factors of 𝑥3– 2𝑥2– 9𝑥 + 18 is (𝑥 + 5)(2𝑥 + 1)(𝑥 − 3).
(iii) It is given that,
(3𝑥 + 2) is a factor of 3𝑥3 + 2𝑥2 – 3𝑥– 2
3𝑥 + 2 = 0
𝑥 = − 2/3
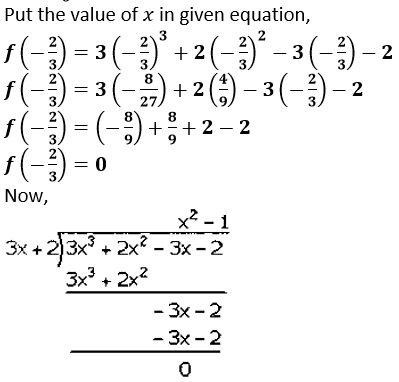
Factorization of 3𝑥3 + 2𝑥3– 3𝑥 − 2 is
(3𝑥 + 2)(𝑥3 − 1)
(3𝑥 + 2)(𝑥 − 1)(𝑥 + 1)
Hence, the factors of 3𝑥3 + 2𝑥3– 3𝑥 − 2 is (3𝑥 + 2)(𝑥 − 1)(𝑥 + 1).
Question 2. Using the Remainder Theorem, factorise each of the following completely.
(𝑖) 3𝑥3 + 2𝑥3 − 19𝑥 + 6
(𝑖𝑖) 2𝑥3 + 𝑥3– 13𝑥 + 6
(𝑖𝑖𝑖) 3𝑥3 + 2𝑥3– 23𝑥– 30
(𝑖𝑣) 4𝑥3 + 7𝑥3 – 36𝑥 – 63
(𝑣) 𝑥3 + 𝑥3 – 4𝑥 – 4
Solution:
(𝑖) 3𝑥3 + 2𝑥3 − 19𝑥 + 6
Assumed that, 3𝑥3 + 2𝑥3 − 19𝑥 + 6 is divided by 𝑥 − 2
𝑥 − 2 = 0
𝑥 = 2
Put the value of 𝑥 in given equation,
3𝑥3 + 2𝑥3 − 19𝑥 + 6 = 0
3(2)3 + 2(2)2 − 19(2) + 6 = 0
3(8) + 2(4) − 19(2) + 6 = 0
24 + 8 − 38 + 6 = 0
38 − 38 = 0
0 = 0
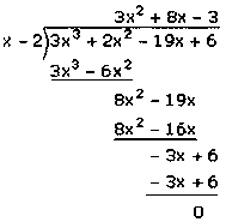
Factorization of 3𝑥3 + 2𝑥2– 19𝑥 + 6 is
(𝑥 − 2)(3𝑥2 − 8𝑥 − 3)
(𝑥 − 2)(3𝑥2 + 9𝑥 − 𝑥 − 3)
(𝑥 − 2)[3𝑥(𝑥 + 3) − 1(𝑥 + 3)]
(𝑥 − 2)(3𝑥 − 1)(𝑥 + 3)
Hence, the factors of 3𝑥3 + 2𝑥2– 19𝑥 + 6 is (𝑥 − 2)(3𝑥 − 1)(𝑥 + 3).
(𝑖𝑖) 2𝑥3 + 𝑥2 – 13𝑥 + 6
Assumed that, 2𝑥3 + 𝑥2– 13𝑥 + 6 is divided by 𝑥 − 2
𝑥 − 2 = 0
𝑥 = 2
Put the value of 𝑥 in given equation,
𝑓(𝑥) = 2(2)3 + (2)2– 13(2) + 6
𝑓(𝑥) = 2(8) + 4– 26 + 6
𝑓(𝑥) = 16 + 4– 26 + 6
𝑓(𝑥) =– 26 + 26
𝑓(𝑥) = 0
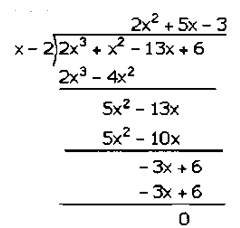
Factorization of 2𝑥3 + 𝑥2 – 13𝑥 + 6 is
(𝑥 − 2)(2𝑥2 + 5𝑥 − 3)
(𝑥 − 2)(2𝑥2 + 6𝑥 − 𝑥 − 3)
(𝑥 − 2)[2𝑥(𝑥 + 3) − 1(𝑥 + 3)]
(𝑥 − 2)(2𝑥 − 1)(𝑥 + 3)
Hence, the factors of 2𝑥3 + 𝑥2– 13𝑥 + 6 is (𝑥 − 2)(2𝑥 − 1)(𝑥 + 3).
(𝑖𝑖𝑖) 3𝑥3 + 2𝑥2– 23𝑥– 30
Assumed that, 3𝑥3 + 2𝑥2– 23𝑥 + 30 is divided by 𝑥 − 2
𝑥 + 2 = 0
𝑥 = −2
Put the value of 𝑥 in given equation,
𝑓(𝑥) = 3(−2)3 + 2(−2)2– 23(−2) + 30
𝑓(𝑥) = 3(−8) + 2(4) + 46 + 30
𝑓(𝑥) = 16 + 4– 26 + 6
𝑓(𝑥) =– 26 + 26
𝑓(𝑥) = 0
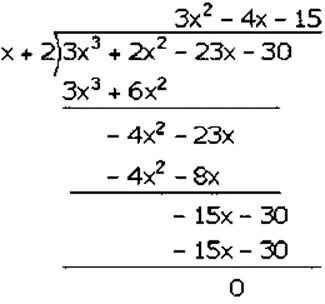
Factorization of 3𝑥3 + 2𝑥2– 23𝑥 − 30 is
(𝑥 + 2)(3𝑥2 − 4𝑥 − 15)
(𝑥 + 2)(3𝑥2+ 5𝑥 − 9𝑥 − 3)
(𝑥 + 2)[𝑥(3𝑥 + 5) − 3(3𝑥 + 5)]
(𝑥 + 2)(3𝑥 + 5)(𝑥 − 3)
Hence, the factors of 3𝑥3 + 2𝑥2– 23𝑥 − 30 is (𝑥 + 2)(3𝑥 + 5)(𝑥 − 3).
(𝑖𝑣) 4𝑥3 + 7𝑥2 – 36𝑥 – 63
Assumed that, 3𝑥3 + 2𝑥2– 23𝑥 + 30 is divided by 𝑥 − 2
𝑥 − 3 = 0
𝑥 = 3
Put the value of 𝑥 in given equation,
𝑓(𝑥) = 4(3)3 + 7(3)2 – 36(3) − 63
𝑓(𝑥) = 4(27) + 7(9) − 36(3) − 63
𝑓(𝑥) = 108 + 63– 108 − 63
𝑓(𝑥) = 0
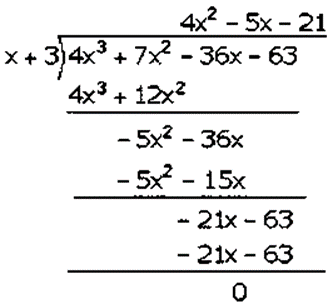
Factorization of 4𝑥3 + 7𝑥2– 36𝑥 − 63 is
(𝑥 + 3)(4𝑥2 − 5𝑥 − 21)
(𝑥 + 3)(4𝑥2 − 12𝑥 + 7𝑥 − 21)
(𝑥 + 3)[4𝑥(𝑥 − 3) + 7(𝑥 − 3)]
(𝑥 + 3)(4𝑥 + 7)(𝑥 − 3)
Hence, the factors of 4𝑥3 + 7𝑥2 – 36𝑥 − 63 is (𝑥 + 3)(4𝑥 + 7)(𝑥 − 3).
(𝑣) 𝑥3 + 𝑥2 – 4𝑥 – 4
Assumed that, 𝑥3 + 𝑥2 – 4𝑥 – 4 is divided by 𝑥 + 1
𝑥 + 1 = 0
𝑥 = −1
Put the value of 𝑥 in given equation,
𝑓(−1) = (−1)3 + (−1)2 – 4(−1) − 4
𝑓(−1) = (−1) + (1) − 4(−1) − 4
𝑓(−1) = −1 + 1 + 4 − 4
𝑓(𝑥) = 0
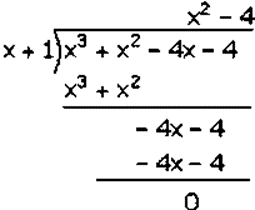
Factorization of 𝑥3 + 𝑥2 – 4𝑥 − 4 is
(𝑥 + 1)(𝑥2 − 4)
(𝑥 + 1)(𝑥2 − (2)2)
(𝑥 + 1)(𝑥 − 2)(𝑥 + 3)
Hence, the factors of 𝑥3 + 𝑥2 – 4𝑥 − 4 is (𝑥 + 1)(𝑥 − 2)(𝑥 + 3).
Question 3. Using the Remainder Theorem, factories the expression 3𝑥3 + 10𝑥2 + 𝑥– 6. Hence, solve the equation 3𝑥3 + 10𝑥2 + 𝑥– 6 = 0.
Solution:
It is given that,
3𝑥3 + 10𝑥2 + 𝑥 – 6
Assumed that, 3𝑥3 + 10𝑥2 + 𝑥– 4 is divided by 𝑥 + 1
𝑥 + 1 = 0
𝑥 = −1
Put the value of 𝑥 in given equation,
𝑓(−1) = 3(−1)3 + 10(−1)2 + (−1) − 6
𝑓(−1) = 3(−1) + 10(1) − 1 − 6
𝑓(−1) = −3 + 10 − 1 − 6
𝑓(−1) = 0
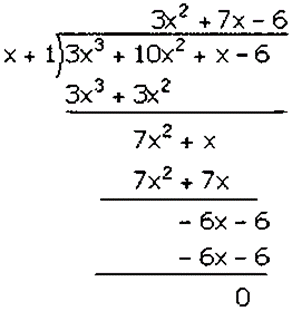
Factorization of 3𝑥3 + 10𝑥2 + 𝑥– 6 is
(𝑥 + 1)(3𝑥2 + 7𝑥 − 6)
(𝑥 + 1)(3𝑥2 + 9𝑥 − 2𝑥 − 6)
(𝑥 + 1)[3𝑥(𝑥 + 3) − 2(𝑥 + 3)]
(𝑥 + 1)(𝑥 + 3)(3𝑥 − 2)
Hence, the factors of 3𝑥3 + 10𝑥2 + 𝑥 − 6 is (𝑥 + 1)(𝑥 + 3)(3𝑥 − 2).
Question 4. Factories the expression 𝑓(𝑥) = 2𝑥3 – 7𝑥2 – 3𝑥 + 18. Hence, find all possible values of x for which 𝑓(𝑥) = 0.
Solution:
It is given that,
2𝑥3 − 7𝑥2 − 3𝑥 + 18
Assumed that, 2𝑥3 − 7𝑥2 − 3𝑥 + 18 is divided by 𝑥 − 2
𝑥 − 2 = 0
𝑥 = 2
Put the value of 𝑥 in given equation,
𝑓(2) = 2(2)3 − 7(2)2 − 3(2) + 18
𝑓(2) = 2(8) + 7(4) − 6 + 18
𝑓(2) = 16 − 28 − 6 + 18
𝑓(2) = 0
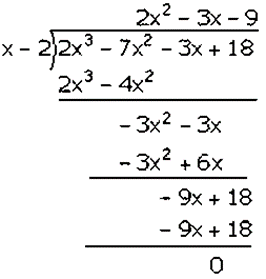
Factorization of 2𝑥3 − 7𝑥2 − 3𝑥 + 18 is
(𝑥 − 2)(2𝑥2 − 3𝑥 − 9)
(𝑥 − 2)(2𝑥2 − 6𝑥 + 3𝑥 − 9)
(𝑥 − 2)[2𝑥(𝑥 − 3) + 3(𝑥 − 3)]
(𝑥 − 2)(𝑥 − 3)(2𝑥 + 3)
Hence, the factors of 2𝑥3 − 7𝑥2 − 3𝑥 + 18 is (𝑥 − 2)(𝑥 − 3)(2𝑥 + 3).
Question 5. Given that 𝑥– 2 and 𝑥 + 1 are factors of 𝑓(𝑥) = 𝑥3 + 3𝑥2 + 𝑎𝑥 + 𝑏; calculate the values of a and b. Hence, find all the factors of 𝑓(𝑥).
Solution:
It is given that,
𝑥3 + 3𝑥2 + 𝑎𝑥 + 𝑏
Assumed that, 𝑥3 + 3𝑥2 + 𝑎𝑥 + 𝑏 is divided by 𝑥 − 2
𝑥 − 2 = 0
𝑥 = 2
Put the value of 𝑥 in given equation,
𝑓(2) = (2)3 + 3(2)2 + 𝑎(2) + 𝑏
𝑓(2) = 8 + 3(4) + 2𝑎 + 𝑏
𝑓(2) = 8 + 12 + 2𝑎 + 𝑏
𝑓(2) = 20 + 2𝑎 + 𝑏
2𝑎 + 𝑏 + 20 = 0______________(i)
Assumed that, 𝑥3 + 3𝑥2 + 𝑎𝑥 + 𝑏 is divided by 𝑥 + 1
𝑥 + 1 = 0
𝑥 = −1
Put the value of 𝑥 in given equation,
𝑓(−1) = (−1)3 + 3(−1)2 + 𝑎(−1) + 𝑏
𝑓(−1) = −1 + 3(1) − 𝑎 + 𝑏
𝑓(−1) = −1 + 3 − 𝑎 + 𝑏
𝑓(−1) = 2 − 𝑎 + 𝑏
2 − 𝑎 + 𝑏 = 0______________(ii)
From equation (i)
2𝑎 + 𝑏 + 20 = 0
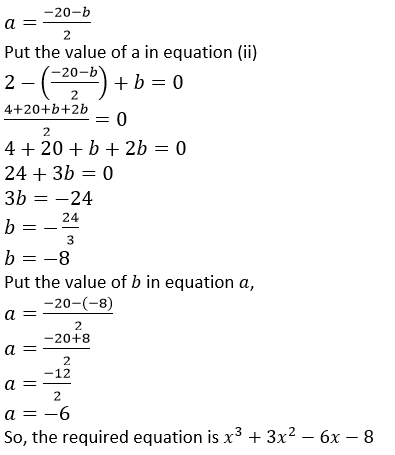
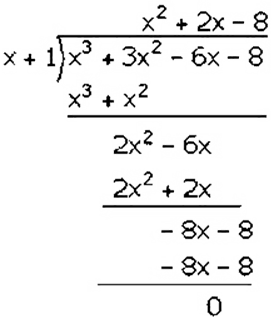
Factorization of 𝑥3 + 3𝑥2 − 6𝑥 − 8 is
(𝑥 + 1)(𝑥2 + 2𝑥 − 8)
(𝑥 + 1)(𝑥2 + 4𝑥 − 2𝑥 − 8)
(𝑥 + 1)[𝑥(𝑥 + 4) − 2(𝑥 + 4)]
(𝑥 + 1)(𝑥 − 2)(𝑥 + 4)
Hence, the factors of 𝑥3 + 3𝑥2 − 6𝑥 − 8 is (𝑥 + 1)(𝑥 − 2)(𝑥 + 4).
Question 6. The expression 4𝑥3– 𝑏𝑥2 + 𝑥– 𝑐 leaves remainders 0 and 30 when divided by 𝑥 + 1 and 2𝑥– 3 respectively. Calculate the values of b and c. Hence, factorize the expression completely.
Solution:
It is given that,
4𝑥3 − 𝑏𝑥2 + 𝑥 − 𝑐 is divided by 𝑥 + 1
𝑥 + 1 = 0
𝑥 = −1
Put the value of 𝑥 in given equation,
𝑓(−1) = 4(−1)3 − 𝑏(−1)2 + (−1) − 𝑐
𝑓(−1) = 4(−1) − 𝑏(1) − 1 − 𝑐
𝑓(−1) = −4 − 𝑏 − 1 − 𝑐
𝑓(−1) = 5 + 𝑏 + 𝑐
5 + 𝑏 + 𝑐 = 0______________(i)
Also,
4𝑥3 − 𝑏𝑥2 + 𝑥 − 𝑐 is divided by 2𝑥 − 3 and leaves remainder 30.
2𝑥 − 3 = 0
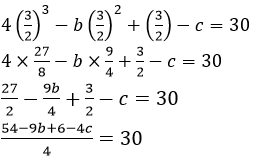
54 − 9𝑏 + 6 − 4𝑐 = 30 × 4
60 − 9𝑏 − 4𝑐 = 120
60 − 9𝑏 − 4𝑐 − 120 = 0
−9𝑏 − 4𝑐 − 60 = 0
−(9𝑏 + 4𝑐 + 60) = 0
9𝑏 + 4𝑐 + 60 = 0______________(ii)
From equation (1) we get the value of 𝑎
5 + 𝑏 + 𝑐 = 0
𝑐 = −5 − 𝑏_(iii)
Put the value of c in equation in equation (ii)
9𝑏 + 4𝑐 + 60 = 0
9𝑏 + 4(−5 − 𝑏) + 60 = 0
9𝑏 − 20 − 4𝑏 + 60 = 0
5𝑏 + 40 = 0
𝑏 = − 40/5
𝑏 = −8
Put the value of b in equation (iii)
𝑐 = −5 − (−8)
𝑐 = −5 + 8
𝑐 = 3
So, the required equation is 4𝑥3 + 8𝑥2 + 𝑥 − 3
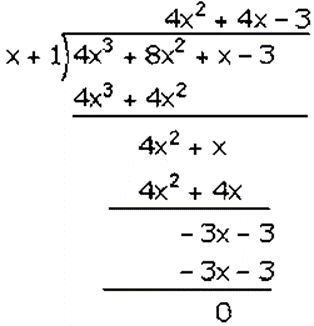
Factorization of 4𝑥3 + 8𝑥2 + 𝑥 − 3 is
(𝑥 + 1)(4𝑥2 + 4𝑥 − 3)
(𝑥 + 1)(4𝑥2 + 6𝑥 − 2𝑥 − 3)
(𝑥 + 1)[2𝑥(2𝑥 + 3) − (2𝑥 + 3)]
(𝑥 + 1)(2𝑥 − 1)(2𝑥 + 3)
Hence, the factors of 4𝑥3 + 8𝑥2 + 𝑥 − 3 is (𝑥 + 1)(2𝑥 − 1)(2𝑥 + 3).
Question 7. If 𝑥 + 𝑎 is a common factor of expressions 𝑓(𝑥) = 𝑥2 + 𝑝𝑥 + 𝑞 and 𝑔(𝑥) = 𝑥2 + 𝑚𝑥 + 𝑛; Show that: 𝑎 = 𝑛−𝑞/𝑚−𝑝
Solution:
It is given that,
𝑓(𝑥) = 𝑥2 + 𝑝𝑥 + 𝑞
𝑥2 + 𝑝𝑥 + 𝑞 is divided by 𝑥 + 𝑎
𝑥 + 𝑎 = 0
𝑥 = −𝑎
(−𝑎)2 + 𝑝(−𝑎) + 𝑞 = 0
𝑎2 − 𝑎𝑝 + 𝑞 = 0
𝑎2 = 𝑎𝑝 − 𝑞(1)
𝑔(𝑥) = 𝑥2 + 𝑚𝑥 + 𝑛
𝑥2 + 𝑚𝑥 + 𝑛 is divided by 𝑥 + 𝑎
𝑥 + 𝑎 = 0
𝑥 = −𝑎
(−𝑎)2 + 𝑚(−𝑎) + 𝑛 = 0
𝑎2 − 𝑎𝑚 + 𝑛 = 0
𝑎2 = 𝑎𝑚 − 𝑛(1)
From equation (1) and (2) we get,
𝑎𝑝 − 𝑞 = 𝑎𝑚 − 𝑛
𝑛 − 𝑞 = 𝑎𝑚 − 𝑎𝑝
𝑛 − 𝑞 = 𝑎(𝑚 − 𝑝)
𝑎 = 𝑛−𝑞/𝑚−𝑝
Hence proved.
Question 8. The polynomials 𝑎𝑥3 + 3𝑥2– 3 and 2𝑥2– 5𝑥 + 𝑎, when divided by 𝑥– 4, leave the same remainder in each case. Find the value of a.
Solution:
Let us assumed that,
𝑓(𝑥) = 𝑎𝑥3 + 3𝑥2– 3
𝑎𝑥3 + 3𝑥2 – 3 is divided by 𝑥– 4
𝑓(4) = 𝑎(4)3 + 3(4)2 – 3
𝑓(4) = 𝑎(64) + 3(16)– 3
𝑓(4) = 64𝑎 + 45_________(1)
Let us assumed that,
𝑔(𝑥) = 2𝑥3– 5𝑥 + 𝑎
2𝑥3– 5𝑥 + 𝑎 is divided by 𝑥– 4
𝑔(4) = 2(4)3– 5(4) + 𝑎
𝑔(4) = 2(64)– 20 + 𝑎
𝑔(4) = 128– 20 + 𝑎
𝑔(4) = 𝑎 + 108_________(2)
From equation (1) and (2)
64𝑎 + 45 = 𝑎 + 108
64𝑎 − 𝑎 = 108 − 45
63𝑎 = 63
𝑎 = 1
Hence, the value of 𝑎 is 1.
Question 9. Find the value of ‘a’, if (𝑥– 𝑎) is a factor of 𝑥3– 𝑎𝑥2 + 𝑥 + 2.
Solution:
Let us assumed that,
𝑓(𝑥) = 𝑥3– 𝑎𝑥2 + 𝑥 + 2
𝑥3– 𝑎𝑥2 + 𝑥 + 2 is divided by 𝑥– 𝑎
𝑥 + 𝑎 = 0
𝑥 = −𝑎
Put the value of 𝑥 in given equation,
(𝑎)3 + 𝑎(𝑎)2 + 𝑎 + 2 = 0
𝑎3 − 𝑎3 + 𝑎 + 2 = 0
𝑎 + 2 = 0
𝑎 = −2
Hence, the value of 𝑎 is −2.
Question 10. Find the number that must be subtracted from the polynomial 3𝑦3 + 𝑦2– 22𝑦 + 15, so that the resulting polynomial is completely divisible by 𝑦 + 3.
Solution:
Let us assumed that,
The number to be subtracted from the given polynomial be k.
𝑓(𝑦) = 3𝑦3 + 𝑦2– 22𝑦 + 15
3𝑦3 + 𝑦2– 22𝑦 + 15 is divisible by (𝑦 + 3).
𝑦 + 3 = 0
𝑦 = −3
Put the value of 𝑦 is −3.
3(−3)3 + (−3)2– 22(−3) + 15– k = 0
3(−27) + 9 + 66 + 15– k = 0
−81 + 9 + 66 + 15 – k = 0
9 – k = 0
k = 9
Hence, the number to be subtracted from the polynomial be 9.
Exercise 8C
Question 1. Show that (𝑥– 1) is a factor of 𝑥3– 7𝑥2 + 14𝑥– 8. Hence, completely factorize the given expression.
Solution:
It is given that,
𝑥3 − 7𝑥2 + 14𝑥 − 8
Assumed that, 𝑥3 − 7𝑥2 + 14𝑥 − 8 is divided by 𝑥 − 1
𝑥 − 1 = 0
𝑥 = 1
Put the value of 𝑥 in given equation,
𝑓(1) = (1)3 − 7(1)2 + 14(1) − 8
𝑓(1) = 1 − 7 − 14 − 8
𝑓(1) = 0
𝑥3 − 7𝑥2 + 14𝑥 − 8 is divided by 𝑥 − 1
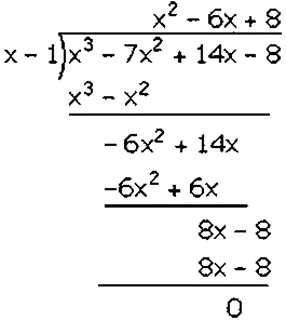
Factorization of 𝑥3 − 7𝑥2 + 14𝑥 − 8 is
(𝑥 − 1)(𝑥2 − 6𝑥 + 8)
(𝑥 − 1)(𝑥2 − 2𝑥 − 4𝑥 + 8)
(𝑥 − 1)[𝑥(𝑥 − 2) − 4(𝑥 − 2)]
(𝑥 − 1)(𝑥 − 2)(𝑥 − 4)
Hence, the factors of 𝑥3 − 7𝑥2 + 14𝑥 − 8 is (𝑥 − 1)(𝑥 − 2)(𝑥 − 4).
Question 2. Using Remainder Theorem, factorize: 𝑥3 + 10𝑥2 – 37𝑥 + 26 completely.
Solution:
It is given that,
𝑥3 + 10𝑥2 − 37𝑥 + 26
Assumed that, 𝑥3 + 10𝑥2 − 37𝑥 + 26 is divided by 𝑥 − 1
𝑥 − 1 = 0
𝑥 = 1
Put the value of 𝑥 in given equation,
𝑓(1) = (1)3 + 10(1)2 − 37(1) + 26
𝑓(1) = 1 + 10 − 37 + 26
𝑓(1) = 37 − 37
𝑓(1) = 0
𝑥3 + 10𝑥2 − 37𝑥 + 26 is divided by 𝑥 − 1
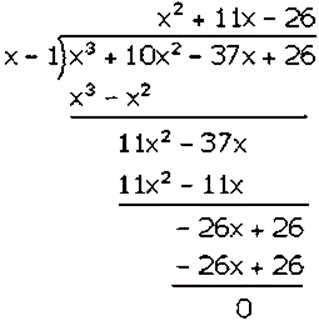
Factorization of 𝑥3 + 10𝑥2 − 37𝑥 + 26 is
(𝑥 − 1)(𝑥2 + 11𝑥 − 26)
(𝑥 − 1)(𝑥2 + 13𝑥 − 2𝑥 − 26)
(𝑥 − 1)[𝑥(𝑥 + 13) − 2(𝑥 + 13)]
(𝑥 − 1)(𝑥 − 2)(𝑥 + 13)
Hence, the factors of 𝑥3 + 10𝑥2 − 37𝑥 + 26 is (𝑥 − 1)(𝑥 − 2)(𝑥 + 13).
Question 3. When 𝑥3 + 3𝑥2– 𝑚𝑥 + 4 is divided by 𝑥– 2, the remainder is 𝑚 + 3. Find the value of m.
Solution:
Let us assumed that,
𝑓(𝑥) = 𝑥3 + 3𝑥2– 𝑚𝑥 + 4
Assumed that, 𝑥3 + 3𝑥2– 𝑚𝑥 + 4 is divided by 𝑥 − 1 and remainder is 𝑚 + 3
𝑥 − 2 = 0
𝑥 = 2
Put the value of 𝑥 in given equation,
(2)3 + 3(2)2
– 𝑚(2) + 4 = 𝑚 + 3
8 + 12– 2𝑚 + 4 = 𝑚 + 3
24– 3 = 𝑚 + 2𝑚
3𝑚 = 21
𝑚 = 7
Hence, the value of 𝑚 is 7.
Question 4. What should be subtracted from 3𝑥3– 8𝑥2 + 4𝑥– 3, so that the resulting expression has 𝑥 + 2 as a factor?
Solution:
Let us assumed that,
The required number be k.
𝑓(𝑥) = 3𝑥3– 8𝑥2 + 4𝑥– 3
Assumed that, 𝑥3 + 3𝑥2– 𝑚𝑥 + 4 is divided by 𝑥 + 2
𝑥 + 2 = 0
𝑥 = −2
Put the value of 𝑥 in given equation,
3(−2)3– 8(−2)2 + 4(−2)– 3– 𝑘 = 0
3(−8)– 8(4) + 4(−2)– 3– 𝑘 = 0
−24 – 32– 8– 3– 𝑘 = 0
−67– 𝑘 = 0
𝑘 = −67
Hence, the required number is -67.
Question 5. If (𝑥 + 1) and (𝑥– 2) are factors of 𝑥3 + (𝑎 + 1)𝑥2– (𝑏– 2)𝑥– 6, find the values of a and b. And then, factorize the given expression completely.
Solution:
Let us assumed that,
𝑓(𝑥) = 𝑥2 + (𝑎 + 1)𝑥2– (𝑏– 2)𝑥– 6
Given that, 𝑥2 + (𝑎 + 1)𝑥2– (𝑏– 2)𝑥– 6 is divided by 𝑥 + 1
𝑥 + 1 = 0
𝑥 = −1
Put the value of 𝑥 in given equation,
(−1)3 + (𝑎 + 1)(−1)2 – (𝑏– 2)(−1)– 6 = 0
−1 + (𝑎 + 1) + (𝑏– 2)– 6 = 0
𝑎 + 𝑏– 8 = 0__________(𝑖)
Given that, 𝑥3 + (𝑎 + 1)𝑥2– (𝑏– 2)𝑥– 6 is divided by 𝑥 + 2
𝑥 + 2 = 0
𝑥 = −2
Put the value of 𝑥 in given equation,
(2)3 + (𝑎 + 1)(2)2 – (𝑏– 2)(2)– 6 = 0
8 + 4𝑎 + 4– 2𝑏 + 4– 6 = 0
4𝑎– 2𝑏 + 10 = 0
2𝑎– 𝑏 + 5 = 0___________(𝑖𝑖)
From equation (i) we get,
𝑎 = 8 − 𝑏__(𝑖𝑖𝑖)
Put the value of a in equation (ii)
2(8 − 𝑏)– 𝑏 + 5 = 0
16 − 2𝑏– 𝑏 + 5 = 0
−2𝑏– 𝑏 = −5 − 16
−3𝑏 = −21
𝑏 = −21/−3
𝑏 = 7
Put the value of b in equation (iii)
𝑎 = 8 − 𝑏
𝑎 = 8 − 7
𝑎 = 1
The required equation is,
𝑓(𝑥) = 𝑥3 + (1 + 1)𝑥2 – (7– 2)𝑥– 6
𝑓(𝑥) = 𝑥3 + 2𝑥2– 5𝑥– 6
Hence, it is proved that (𝑥 + 1)(𝑥– 2) are factor of 𝑥3 + 2𝑥2– 5𝑥– 6.
Factorization of 𝑥3 + 10𝑥2 − 37𝑥 + 26 is
(𝑥 − 1)(𝑥 − 2)(𝑥 + 3)
Hence, the factors of 𝑥3 + 2𝑥2 − 5𝑥 − 6 is (𝑥 + 1)(𝑥 − 2)(𝑥 + 3).
Question 6. If 𝑥– 2 is a factor of 𝑥2 + 𝑎𝑥 + 𝑏 and a + b = 1, find the values of a and b.
Solution:
It is given that,
𝑎 + 𝑏 = 1_______(𝑖)
Also,
Given that, 𝑥2 + 𝑎𝑥 + 𝑏 is divided by 𝑥 − 2
𝑥 − 2 = 0
𝑥 = 2
Put the value of 𝑥 in given equation,
(2)2 + 𝑎(2) + 𝑏 = 0
4 + 2𝑎 + 𝑏 = 0
2𝑎 + 𝑏 = −4 _(𝑖𝑖)
From equation (i),
𝑎 + 𝑏 = 1
𝑎 = 1 − 𝑏(𝑖𝑖𝑖)
Put the value of a in equation (ii),
2(1 − 𝑏) + 𝑏 = −4
2 − 2𝑏 + 𝑏 = −4
−𝑏 = −4 − 2
−𝑏 = −6
𝑏 = 6
Put the value of a in equation (iii),
𝑎 = 1 − 𝑏
𝑎 = 1 − 6
𝑎 = −5
Hence, the value of 𝑎 is -5 and 𝑏 is 6
Question 7. Factorise 𝑥3 + 6𝑥2 + 11𝑥 + 6 completely using factor theorem.
Solution:
It is given that,
𝑥3 + 6𝑥2 + 11𝑥 + 6
Assumed that, 𝑥3 + 6𝑥2 + 11𝑥 + 6 is divided by 𝑥 + 1
𝑥 + 1 = 0
𝑥 = −1
Put the value of 𝑥 in given equation,
𝑓(−1) = (−1)3 + 6(−1)2 + 11(−1) + 6
𝑓(−1) = −1 + 6 − 11 + 6
𝑓(−1) = 12 − 12
𝑓(−1) = 0
𝑥3 + 6𝑥2 + 11𝑥 + 6 is divided by 𝑥 + 1
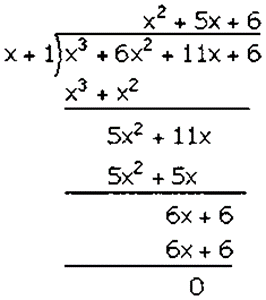
Factorization of 𝑥3 + 6𝑥2 + 11𝑥 + 6 is
(𝑥 + 1)(𝑥2 + 5𝑥 + 6)
(𝑥 + 1)(𝑥2 + 2𝑥 + 3𝑥 + 6)
(𝑥 + 1)[𝑥(𝑥 + 2) + 3(𝑥 + 2)]
(𝑥 + 1)(𝑥 + 2)(𝑥 + 3)
Hence, the factors of 𝑥3 + 6𝑥2 + 11𝑥 + 6 is (𝑥 + 1)(𝑥 + 2)(𝑥 + 3).
Question 8. Find the value of ‘𝑚’, if 𝑚𝑥2 + 2𝑥2– 3 and 𝑥2– 𝑚𝑥 + 4 leave the same remainder when each is divided by 𝑥– 2.
Solution:
Let us assumed that,
𝑓(𝑥) = 𝑚𝑥2 + 2𝑥2– 3
𝑔(𝑥) = 𝑥2– 𝑚𝑥 + 4
According to the question,
𝑓(𝑥) and 𝑔(𝑥) leave the same remainder if divided by (𝑥– 2).
𝑥– 2 = 0
𝑥 = 2
We have,
𝑓(2) = 𝑔(2)
𝑚(2)3 + 2(2)2– 3 = (2)2– 𝑚(2) + 4
𝑚(8) + 2(4)– 3 = 4– 2𝑚 + 4
8𝑚 + 8– 3 = 4– 2𝑚 + 4
8𝑚 + 2𝑚 = 4 + 4 − 8 + 3
10𝑚 = 3
𝑚 = 3/10
Hence, the value of 𝑚 is 3/10.
Question 9. The polynomial 𝑝𝑥3 + 4𝑥2– 3𝑥 + 𝑞 is completely divisible by 𝑥2– 1; find the values of p and q. Also, for these values of p and q factorize the given polynomial completely.
Solution:
Let us assumed that,
𝑓(𝑥) = 𝑝𝑥3 + 4𝑥2– 3𝑥 + 𝑞
According to the question,
𝑝𝑥3 + 4𝑥2– 3𝑥 + 𝑞 is divisible by (𝑥2– 1) = (𝑥 + 1)(𝑥– 1).
𝑓(1) = 0 𝑎𝑛𝑑 𝑓(−1) = 0
𝑓(1) = 𝑝(1)3 + 4(1)2– 3(1) + 𝑞 = 0
𝑓(1) = 𝑝 + 4– 3 + 𝑞 = 0
𝑝 + 𝑞 + 1 = 0 (𝑖)
From (𝑥 + 1) we get,
𝑓(−1) = 𝑝(−1)3 + 4(−1)2– 3(−1) + 𝑞 = 0
𝑓(−1) = 𝑝(−1) + 4(1)– 3(−1) + 𝑞 = 0
𝑓(−1) = −𝑝 + 4(1) + 3 + 𝑞 = 0
−𝑝 + 𝑞 + 7 = 0__________(𝑖𝑖)
From equation (i) we get,
𝑝 + 𝑞 + 1 = 0
𝑝 = −1 − 𝑞__(𝑖𝑖𝑖)
Put the value of p in equation (ii)
−𝑝 + 𝑞 + 7 = 0
−(−1 − 𝑞) + 𝑞 + 7 = 0
1 + 𝑞 + 𝑞 + 7 = 0
2𝑞 + 8 = 0
𝑞 = −4
Put the value of q in equation (iii)
𝑝 = −1 − 𝑞
𝑝 = −1 − (−4)
𝑝 = −1 + 4
𝑝 = 3
Hence, the required equation is 𝑓(𝑥) = 3𝑥3 + 4𝑥2– 3𝑥– 4.
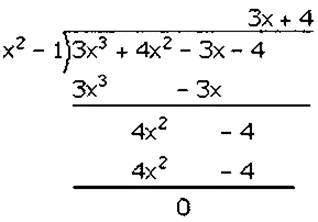
Factorization of 3𝑥3 + 4𝑥2– 3𝑥– 4 is
(𝑥2 − 1)(3𝑥 + 4)
(𝑥 − 1)(𝑥 + 1)(3𝑥 + 4)
Hence, the factors of 3𝑥3 + 4𝑥2– 3𝑥– 4 is (𝑥 − 1)(𝑥 + 1)(3𝑥 + 4).
Question 10. Find the number which should be added to 𝑥2 + 𝑥 + 3 so that the resulting polynomial is completely divisible by (𝑥 + 3).
Solution:
Let us assumed that, the required number be k.
𝑓(𝑥) = 𝑥2 + 𝑥 + 3 + 𝑘
According to the question,
𝑥2 + 𝑥 + 3 + 𝑘 is divisible by (𝑥 + 3) and remainder is 0.
𝑥 + 3 = 0
𝑥 = −3
Put the value of x in given equation,
(−3)2 + (−3) + 3 + 𝑘 = 0
9– 3 + 3 + 𝑘 = 0
9 + 𝑘 = 0
𝑘 = −9
Hence, the required number is -9.
Question 11. When the polynomial 𝑥3 + 2𝑥2– 5𝑎𝑥– 7 is divided by (𝑥– 1), the remainder is A and when the polynomial 𝑥3 + 𝑎𝑥2– 12𝑥 + 16 is divided by (𝑥 + 2), the remainder is B. Find the value of ‘a’ if 2𝐴 + 𝐵 = 0.
Solution:
According to question,
𝑥3 + 2𝑥2– 5𝑎𝑥– 7 is divided by (𝑥– 1), the remainder is A.
𝑥– 1 = 0
𝑥 = 1
Put the value of 𝑥 in given equation,
𝑥3 + 2𝑥2– 5𝑎𝑥– 7 = 𝐴
1 + 2– 5𝑎 − 7 = 𝐴
– 5𝑎– 4 = 𝐴____(𝑖)
𝑥3 + 𝑎𝑥2 – 12𝑥 + 16 is divided by (𝑥 + 2), the remainder is B.
𝑥 + 2 = 0
𝑥 = −2
Put the value of 𝑥 in given equation,
𝑥3 + 𝑎𝑥2 – 12𝑥 + 16 = 𝐵
(−2)3 + 𝑎(−2)2– 12(−2) + 16 = 𝐵
−8 + 4𝑎 + 24 + 16 = 𝐵
4𝑎 + 32 = 𝐵_(𝑖𝑖)
It is given that 2A + B = 0
From equation (i) and (ii), we get,
2(−5𝑎– 4) + 4𝑎 + 32 = 0
−10𝑎– 8 + 4𝑎 + 32 = 0
−6𝑎 + 24 = 0
6𝑎 = 24
𝑎 = 4
Hence, the value of 𝑎 is 4.
Question 12. (3𝑥 + 5) is a factor of the polynomial (𝑎– 1)𝑥3 + (𝑎 + 1)𝑥2– (2𝑎 + 1)𝑥– 15. Find the value of ‘a’, factorize the given polynomial completely.
Solution:
Let us assumed that,
𝑓(𝑥) = (𝑎 − 1)𝑥3 + (𝑎 + 1)𝑥2 − (2𝑎 + 1)𝑥 − 15
According to question,
(3𝑥 + 5) is a factor of 𝑓(𝑥) and remainder = 0
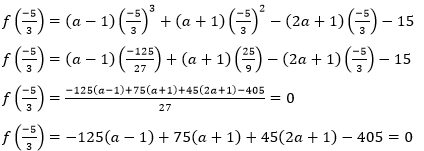
−125(𝑎 − 1) + 75(𝑎 + 1) + 45(2𝑎 + 1) − 405 = 0
40𝑎 − 160 = 0
40𝑎 = 160
𝑎 = 4
𝑓(𝑥) = (𝑎 − 1)𝑥3 + (𝑎 + 1)𝑥2 − (2𝑎 + 1)𝑥 − 15
𝑓(𝑥) = (4 − 1)𝑥3 + (4 + 1)𝑥2 − (2(4) + 1)𝑥 − 15
𝑓(𝑥) = 3𝑥3 + 5𝑥2 − 9𝑥 − 15
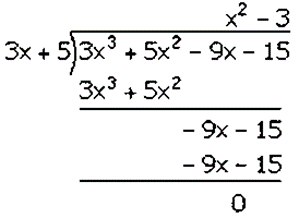
Factorization of 3𝑥3 + 5𝑥2– 9𝑥– 15 is
(3𝑥 + 5)(𝑥2 − 3)
(3𝑥 + 5)(𝑥 + √3)(𝑥 − √3)
Hence, the factors of 3𝑥3 + 5𝑥2– 9𝑥– 15 is (3𝑥 + 5)(𝑥 + √3)(𝑥 − √3).
Question 13. When divided by 𝑥– 3 the polynomials 𝑥3– 𝑝𝑥2 + 𝑥 + 6 and 2𝑥3– 𝑥2– (𝑝 + 3)𝑥– 6 leave the same remainder. Find the value of ‘p’.
Solution:
It is given that,
(𝑥– 3) is factor of 𝑓(𝑥) = 𝑥3– 𝑝𝑥2 + 𝑥 + 6,
𝑓(3) = (3)3– 𝑝(3)2 + 3 + 6
𝑓(3) = 27– 9𝑝 + 3 + 6
𝑓(3) = 36– 9𝑝
(𝑥 – 3) is factor of 𝑔(𝑥) = 2𝑥3– 𝑥2 + (𝑝 + 3) − 6
𝑔(3) = 2(3)3– (3)2– (𝑝 + 3)(3)– 6
𝑔(3) = 2(27)– 9– (𝑝 + 3)(3)– 6
𝑔(3) = 54– 9– 3𝑝 + 9– 6
𝑔(3) = 30 − 3𝑝
It is also given that both the sides have equal remainder,
𝑓(3) = 𝑔(3)
36– 9𝑝 = 30– 3𝑝
6𝑝 = −6
𝑝 = 1
Hence, the value of 𝑝 is 1.
Question 14. Use the Remainder Theorem to factorise the following expression: 2𝑥3 + 𝑥2– 13𝑥 + 6.
Solution:
Let us assumed that,
𝑓(𝑥) = 2𝑥3 + 𝑥2 − 13𝑥 + 6
By Remainder theorem,
Put the 𝑥 = 2, we get,
𝑓(2) = 2(2)3 + (2)2 − 13(2) + 6
𝑓(2) = 2(8) + 4 − 26 + 6
𝑓(2) = 16 + 4 − 26 + 6
𝑓(2) = 0
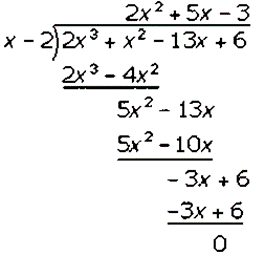
Factorization of 2𝑥2 + 5𝑥 − 3 is
(𝑥 − 2)(2𝑥2 + 6𝑥 − 𝑥 − 3)
(𝑥 − 2)[2𝑥(𝑥 + 3) − 1(𝑥 + 3)]
(𝑥 − 2)(2𝑥 − 1)(𝑥 + 3)
Hence, the factors of 2𝑥3 + 𝑥2– 13𝑥 + 6 is (𝑥 − 2)(2𝑥 − 1)(𝑥 + 3).
Question 15. Using remainder theorem, find the value of k if on dividing 2𝑥3 + 3𝑥2– 𝑘𝑥 + 5 by 𝑥– 2, leaves a remainder 7.
Solution:
Let us assumed that,
𝑓(𝑥) = 2𝑥3 + 3𝑥2– 𝑘𝑥 + 5
By Remainder Theorem,
𝑓(2) = 7
2(2)3 + 3(2)2– 𝑘(2) + 5 = 7
2(8) + 3(4) – 2𝑘 + 5 = 7
16 + 12 – 2𝑘 + 5 = 7
33 – 2𝑘 = 7
2𝑘 = 26
𝑘 = 13
Hence, the value of 𝑘 is 13.
Question 16. What must be subtracted from 16𝑥3 – 8𝑥2 + 4𝑥 + 7 so that the resulting expression has 2𝑥 + 1 as a factor?
Solution:
Let us assumed that,
𝑓(𝑥) = 16𝑥3– 8𝑥2 + 4𝑥 + 7
It is given that 2𝑥 + 1 is a factor of 16𝑥3– 8𝑥2 + 4𝑥 + 7.
2𝑥 + 1 = 0
2𝑥 = −1
𝑥 = − 1/2
Put the value 𝑥 in given equation,