Are you looking for Mathematics Formulas ICSE Class 10, then you have come to the correct place. On this page, we have provided Class 10 Mathematics Chapter-wise formulas for all important topics which are covered in your Mathematics books. You can use these formula banks for ICSE for revision just prior to your exams or for daily use too. Its important for you to remember these formulas they will be really useful when you solve mathematics problems.
ICSE MATHEMATICS (X)
The paper will be divided into two Sections. Section I (40 marks), Section II (40 marks). Section I: It will consist of compulsory short answer questions. Section II: Candidates will be required to answer four out of seven questions.
UNITS & CHAPTERS
1. COMMERCIAL ARITHMETIC
• Compound Interest (Paying back in equal installments not included)
• Sales Tax and Value Added Tax
• Banking (Saving Bank Accounts and Recurring Deposit Accounts)
• Shares and Dividends (Brokerage and fractional shares not included)
2. ALGEBRA
• Linear Inequations
• Quadratic Equations and Solving Problems
• Ratio and Proportion Remainder and Factor Theorems (f(x) not to exceed degree 3)
• Matrices
3. CO-ORDINATE GEOMETRY
• Reflection
• Distance and Section Formulae
• Equation of a Straight Line
4. GEOMETRY
• Symmetry
• Similarity
• Loci (Locus and Its Constructions)
• Circles Tangents and Intersecting
• Chords
• Constructions (tangents to circle, circumscribing & inscribing circle on △ & reg. hexagon)
5. MENSURATION
• Circumference and Area of a circle (Area of sectors of circles other than semi-circle and quarter-circle not included)
• Surface Area and Volume (of solids)
6. TRIGONOMETRY
• Trigonometrical Identities and Trigonometrical Tables
• Heights and Distances (Cases involving more than 2 right angled △ട excluded)
7. STATISTICS
• Graphical Representation (Histogram and Ogives)
• Measures of Central Tendency (Mean, Median, Quartiles and Mode)
• Probability
Commercial Arithmetic
a) Goods and Service Tax [GST]
What is GST
GST is a comprehensive tax levy on manufacture, sale and consumption of goods and service at a national level under which no distinction is made between goods and services for levying of tax. It substitutes all the indirect taxes levied on goods and services by the Central and State government in India. GST is a tax on goods and services under which every person is liable to pay tax on his output and is entitled to get Input Tax Credit, (ITC) on the tax paid on its inputs and ultimately the final consumer shall bear the tax.
Objective of GST One of the main objective of GST is to eliminate the double taxation on production and
distribution cost of goods and services. The exclusion of cascading effects, that is, tax on tax till the level of final consumers will significantly improve the competitiveness of original goods and
services in market which will have a beneficial impact on the GDP of the country.
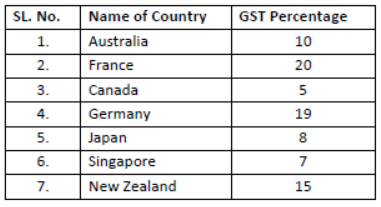
Worldwide GST France was the first country to introduce GST in 1954. GST rates of seven countries are mentioned below:
GST Computation
Applicable GST rates in India are 5%, 12%, 18% or 28%.
Say, goods are sold at the rate of Rs.500. GST rate is 18%. Then Gross amount of the goods is
= 500 + [500 ×(18/100) ] = Rs.590.
Types of Problems Included in syllabus
i) Computation of tax including discounts
ii) List-price
iii) Profit and Loss
iv) Basic / Cost Price including inverse cases
Formulae
Add GST
GST Amount = Original Cost × GST % / 100
Net Price = Original Cost + GST Amount
Remove GST
GST Amount = Original Cost –[ Original Cost × (100 / 100+GST)]
Net Price = Original Cost – GST Amount
b) Banking
Types of accounts
i) SB = Savings accounts in which simple interest is offered.
ii) FD = Fixed Deposit, that is, a sum of money is deposited for a fixed period, and so more rate of interest is offered.
iii) RD = Recurring Deposit, that is, certain fixed sum is deposited every month, and interest rate offered is usually more than SB, but less than FD.
Formulae 1. For SB account simple interest (SI) is offered.
SI = P x R x T / 100
where P = Principal amount, R = rate of interest, T = Time.
For Recurring Deposit Account
Matured Amount = Total sum deposit + Interest on it
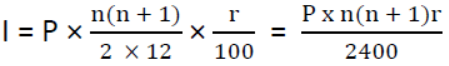
where P = Each Installment, r = rate per annum, n = number of months
(The sum of Natural Numbers: S = 1 + 2 + 3 + – – – + N = N( N+1) /2 )
MV = P(n) + I,
Where MV = Matured Value, P(n) = Total Sum Deposited, I = Interest
c) Shares and Dividends
Nominal Value = Face Value = Par Value = FV
Market Value = MV
Dividend = Income
Types of Problems Included in syllabus
i) Computation of MV/FV
ii) Market value
iii) Dividend
iv) Rate of Dividend
v) Premium
Formulae
1. Income = No. of Shares × Rate of Dividend × FV
2.No. of Shares = Total Nominal Value / Nominal Value per shares
or Investment / Market Value of each share
3. Investment = No. of Shares X MV per share
4. Total Nominal Value= No. of Shares X FV per shares
5. Dividend (Income) = NV/MV × Investment × Dividend%
6. Sales proceeds = No. of Shares X Selling Price of Each Share
7. Rate of Dividend = Profit % or Yield % or Return% = Income / Investment x 100
8. Earning = NV/MV × Investment × Rate of Dividend
9. For better investment, compare the Yield% of both shares
10. Discount Shares means Market Value < Face value
11. Premium Share means Market Value > Face Value
12. Share at par means Market Value = Face Value
Compound Interest:
✔ A = P + I
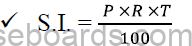
✔ S.I. for 1st year = C.I. for 1st year
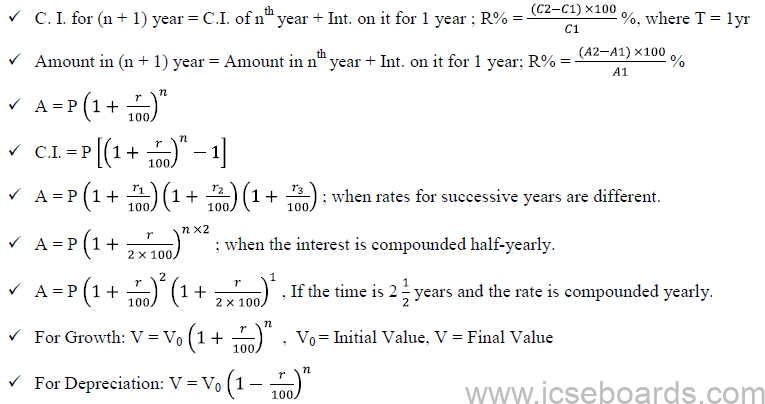
Sales Tax and Value Added Tax:
✔ The price at which an Article is marked : List Price/Marked Price/Printed Price/Quoted Price
✔ Sale Price = M.P. – Discount, Discount is calculated on M.P.
✔ Sales Tax is calculated after deducting the discount (on the discounted price).
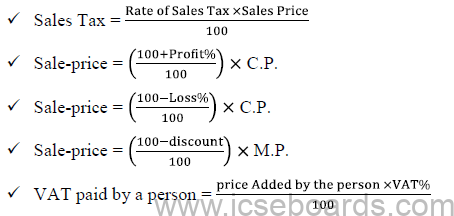
✔ VAT = Tax recovered(charged) on the sale – Tax paid on the purchase
Banking:
1. SB Account:
a. Withdrawal = Debit
b. Deposit = Credit
c. Steps for calculation of interest:
i. Find the minimum balance of each month between 10th day and the last day.
ii. Add all the balances. This is the Equivalent Monthly Principal for 1 month.
iii. Calculate the SI on the Equivalent Monthly Principal with T = 1/12 years.
iv. No interest is paid for the month in which the account is closed.
v. If the Amount Received on closing is asked, add the interest to the LAST BALANCE and not to the Equivalent Monthly Principal.
2. RD Account:
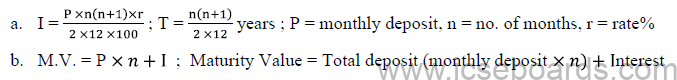
Shares and Dividend:
⩥ The total money invested by the company is called its capital stock.
⩥ The capital stock is divided into a number of equal units. Each unit is a called a share.
⩥ Nominal Value is also called Register Value, Printed Value, and Face Value.
⩥ The FV of a share always remains the same, while its MV goes on changing.
⩥ The part of the profit of a company which is distributed amongst the shareholders is known as dividend.
⩥ If the MV of the share is same as its NV, the share is said to be at par.
⩥ If the MV of the share is greater than NV, the share is said to be at premium.
⩥ If the MV of the share is less than NV, the share is said to be at discount

Algebra
a) Linear Inequations
Linear Inequation is one unknown variable for x ε N, W, Z and R.
i) Natural numbers (N) = {1, 2, 3, 4, 5, … ∞}
ii) Whole numbers (W) = {0, 1, 2, 3, 4, 5, … ∞} (W0N)
iii) Integers (I, Z) = {-∞, ….-3, -2, -1, 0, 1, 2, 3, 4, 5, … ∞}
iv) Real numbers (R) = {-∞, ….0 … ∞} (all decimals and fractions in between are included)
Types of Problems Included in syllabus
i) Solving algebraically and writing the solution in set notation form
ii) Representation of solution on the number line
Inequation signs
i) The sign ‘ < ’ means ‘is less than’.
ii) The sign ‘>’ means ‘is greater than’.
iii) The sign ‘≤’ means ‘is less or equal to’.
iv) The sign ‘ ≥ ’ means ‘is less or equal to’.
Rules
i) By adding equal number to both sides of an inequation, sign remains unchanged.
ii) By subtracting equal number from both sides of an inequation, sign remains unchanged.
iii) Multiplying by a positive equal number to both sides of an inequation, sign remains unchanged.
iv) Dividing by a positive equal number to both sides of an inequation, sign remains unchanged.
v) Multiplying or dividing by only equal negative number, inequation sign becomes opposite, that is, from ‘ < ’ becomes ‘>’, from ‘≤’ becomes ‘≥’.
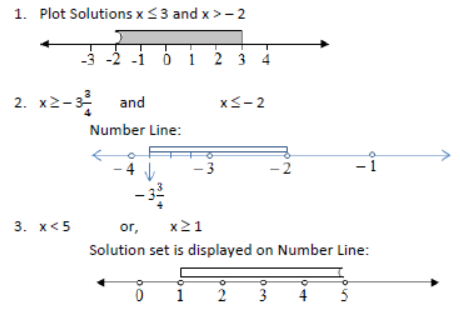
Number Lines
Please note –
i) A number line should have arrow sign at both ends of the line.
ii) You should show at least one number more at both ends of the marking on the line. Say,
b) Quadratic Equations
Types of Problems Included in syllabus
i) Solving Quadratic Equations by – Factorization and Using Formula
ii) Solving simple quadratic equation problems
Formulae Standard form of the Quadradic Equation = ax2 + bx + c = 0, (a≠0)

Characteristics of D – Nature of Roots:
a) If D = 0, then the roots will be equal and real. Lines are coincident
b) If D > 0, and is perfect square, then the roots will be real, unequal and rational. Lines are intersecting
c) If D > 0, and is not perfect square, then the roots will be real, unequal and irrational.
d) If D < 0, the roots will be imaginary. Parallel lines.
- If α and β are the roots of a quadratic equation, then:
a) α + β = – b/a
b) α × β = c/a - Quadratic Equation: x2 – (α + β) x + α × β = 0.
c) Ratio and Proportion
i) If a, b, c & d are in proportion a/b = c/d i.e. ad = bc (product of means = product of extremes) also called in proportion.
ii) If a, b & c are in proportion a/b = c/d , i.e. b2 = ac (where ‘b’ is the mean proportion and ‘c’ is the third proportion) also called continued proportion.
iii) If a, b, c & d are in continued proportion a/b = b/c = c/d K, Then c = dk, b = dk2, a = dk3.
iv) If a, b, c & d are in proportion then use property of ratio.
Types of Problems Included in syllabus
i) Proportion
ii) Componendo, Dividendo, Alternendo, Invertendo Properties and their Combinations
iii) Direct simple applications on proportions only
Formulae
1. a/c = b/d By Alternendo
2. b/a = d/c By Invertendo
3. (a+b)/b = (c+d)/d By Componendo
4. (a-b)/b = (c-d)/d By Dividendo
5. (a+b) /(a-b) = (c+d)/(c-d) By Comp & Div
6. a/b = c/d = e/f = a+c+e / b+d+f By Property of ratio
d) Factorization of Polynomials
Types of Problems Included in syllabus
i) Problems based on Factor Theorm and Remainder Theorem
ii) Factorising a polynomial completely after obtaining one factor by factor theorem
Theorem
• Factor Theorem
When a polynomial f(x) is divided by x – a, the remainder = f (a). And, if remainder f(a)= 0; x – a is a factor of polynomial f(x). OR if (x – a) is a factor, the remainder is 0.
• Remainder Theorem
If f(x) is a polynomial, an expression with variable ‘x’ and is divided by (x– a); the remainder
is the value of f(x) at x = a. i.e. the remainder is f(a)
• Complete factorizing
Let f(x) be a Polynomial, divided by g(x), quotient be q(x), which leaves a remainder r(x).
Then f(x) = g(x) × q(x) + r(x).
That is, Dividend = Divisor × Quotient + Remainder
Note: f(x) not to exceed degree 3
e) Matrices
1. Order of a matrix – Row and column Matrix Size of Matrix = No. of rows x No. of columns. (Rh →Rows horizontal)
2. Compatibility of Addition and Multiplication
Matrix A m x n can only be multiplied with matrix B p x q if n = p and then resultant matrix will have m rows and q cols i.e. R m x q
Matrix multiplication is not commutative if AB ≠ BA
Matrix multiplication is associative if A(BC) = (AB)C
A X 1=1 X A =where I is a unit matrix of suitable order
3. Distributive Property A (B+C) = AB+AC
If AB = AC then B ≠ C, A may or may not be zero.
Null and Identity Matrix
Null matrix =

Identity Matrix =
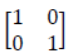
5. Addition and Subtraction of 2 X 2 Matrices
Only same order matrix can be added or subtracted
6. Multiplication of 2 X 2 Matrix by non – zero rational number and another matrix
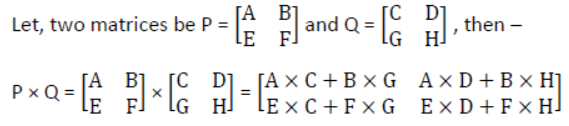
f) Arithmetic and Geometric Progression
Types of Problems Included in syllabus
i) Finding the general term
ii) Finding sum of the first n’ terms
iii) Simple Application
Arithmetic Progression
If you have the sequence 2, 8, 14, 20, 26, then each term is 6 more than the previous term. This is an example of an arithmetic progression (AP) and the constant value that defines the difference between any two consecutive terms is called the common difference.
Formulae
1. Finding their General Terms
If an arithmetic difference has a first term a and a common difference of d, then we can write a,
(a + d), (a + 2d) … {a + (n-1) d}
where the nth term = a + (n−1) d
2. Finding the Sum of First nTH terms
Sum of Arithmetic series
The sum of an arithmetic series of n terms is found by making n/2 pairs each with the value of the sum of the first and last term.
This gives us the formula:
Sn =n/2 (a+1)
where a = first term and l= last term.
As the last term is the nth term = a + (n − 1) d we can rewrite this as:
Sn =n/2 (2a + (n-1)d)
3. Simple Applications
Use the first formula if you know the first and last terms; use the second if you know the first term and the common difference.
Geometric Progression Geometric Sequence is a sequence such that any element after the first is obtained by
multiplying the preceding element by a constant called the Common Ratio which is denoted by ‘r’. The common ratio (r) is obtained by dividing any term by the preceding term, that is –
r = a2 /a1 or a2 /a2
so, r= an / an-1
where, r = common ratio,
a1= first term
a2= second term
a3= third term, and
So, Tn= nth term.
Thus, Geometric Sequence is called the Geometric Progression, in short, GP.
Example:
The sequence 1, 2, 4, 8, 16, – – – is a geometric sequence.
Here, a = 1, r = 2/1 = 2,
or, r = 4/2 = 2 etc.
The geometric sequence has its sequence formation:
a1, a1r, a1r2, a1r3, – – -, a1rn-1 , a1rn.
Formulae
- 1. Common Term = an= a1rn-1
- 2. Sum of nth Term = Sn= a1 (1-rn) / 1-r , when r < 1
- 3. Also, Sn= a1 (rn -1 ) / r-1 , when r > 1
Linear Inequations:
✔ The signs >,< ≥ are ≤ called signs of inequality.
✔ On transferring +ve term becomes –ve and vice versa.
✔ If each term is multiplied or divided by +ve number, the sign of inequality remains the same.
✔ The sign of inequality reverses:
⩥ If each term is multiplied or divided by same negative number.
⩥ If the sign of each term on both the sides of an inequation is changed.
⩥ On taking reciprocals of both sides, in case both the sides are positive or negative.
✔ Always, write the solution set for the inequation, e.g.,{x : x≤3, x ∈ N}, solution set = {1, 2, 3}
✔ To represent the solution on a number line:
⩥ Put arrow sign on both the ends of the line and keep extra integers beyond the range.
⩥ Use dark dots on the line for each element of N, W and Z.
⩥ For Q, R: mark range with solid circle ⚫ (for ≥ or ≤), hollow circle ⚪ (for < and >.)
✔ “and” means Intersection ( only common elements of the sets).
✔ “or” means Union(all elements of the sets without repetition).
Quadratic Equations:
1. Quadratic equation is an equation with one variable, the highest power of the variable is 2.
2. Some useful results:
a) (a + b)2 = a2 + b2 + 2ab
b) (a – b)2 = a2 + b2 – 2ab
c) a2 – b2= (a + b) (a – b)
d) (a + b)2 – (a – b)2 = 4ab
e) (a + b)3 = a3 + b3 + 3ab(a + b)
f) (a – b)3 = a3 – b3 – 3ab(a – b)
g) (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
h) a3 + b3 + c3 – 3abc = (a + b + c) (a2 + b2 + c2 – ab – bc – ca)
3. Steps for solving quadratic equation by factorization:
a. Clear all fractions and brackets if necessary.
b. Bring it to the form ax2 + bx + c = 0 by transposing terms.
c. Factorize the expression by splitting the middle term as a sum of product of a and c.
4. Discriminant (D) = b2 – 4ac
a. if D > 0, then the roots are real and unequal
b. if D = 0, then the roots are real and equal
c. if D < 0, then the roots are not real (imaginary).
5. The roots of the quadratic equation ax2 + bx + c = 0 ; a ≠ 0 can be obtained by using the formula:
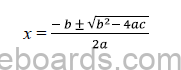
Ratio and Proportion:
• A ratio is a comparison of the sizes of two or more quantities of the same kind by division. Since ratio is a number, so it has no units.
• To find the ratio between two quantities, change them to the same units.
• To compare two ratios, convert them into like fractions.
• In the ratio, a : b, a is called antecedent and b is called consequent.
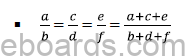
• Compound ratio of a : b and c : d is (a × c) : (b × d)
• Duplicate ratio of a : b is a2 : b2
• Triplicate ratio of a : b is a3 : b3
• Sub-duplicate ratio of a : b is √a: √b
• Sub-triplicate ratio of a : b is :
• Reciprocal ratio of a : b is 3√a: 3√b
• Proportion- An equality of two ratios is called a proportion. Written as: a : b :: c : d or a/b = c/d
• Product of extreme terms = product of middle terms, if a, b, c, d are in proportion then ad = bc
• Continued Proportion- a : b :: b : c or a : b = b : c ; mean proportion (b) =√ab
• Invertendo – If a : b = c : d, then b : a = d : c
• Alternendo – If a : b = c : d, then a : c = b : d
• Componendo – If a : b = c : d, then a + b : b = c + d : d
• Dividendo – If a : b = c : d, then a – b : b = c – d : d
• Componendo and Dividendo – If a : b = c : d, then a + b : a – b = c + d : c – d
Remainder and Factor Theorem:
1. If f (x) is a polynomial, which is divisible by (x – a), a ∈ R, then the remainder is f (a).
2. If the remainder on dividing a polynomial f (x) by (x – a), f (a) = 0, then (x – a) is a factor of f (x).
3. When f (x) is divided by (ax + b), then remainder is f (-b/a), a ≠ 0
4. When f (x) is divided by (ax – b), then remainder is f ,(b/a) a 0
Matrices:
1. A rectangular arrangement of numbers, in the form of horizontal (rows) and vertical lines (columns) is called a matrix. Each number of a matrix is called its element. The elements of a matrix are enclosed in brackets [ ].
2. The order of a matrix = No. of rows × No. of columns
3. Row matrix: Only 1 row. [a b]
4. Column matrix: Only 1 column. [a/b]


Coordinate Geometry
Co-ordinate Geometry
Reflection
For any points
P (a, b) Mx→P’ (a, –b) Reflected in x axis
P (a, b) My→P’ (-a, b) Reflected in y axis
P (a, b) Mo→P’ (-a, -b) Reflected in origin
Invariant point is a point which does not change under reflection.
E.g. P (2, 0) Mx →P’ (2, 0)
Coordinates
Formulae
1. Distance Formula
The distance between two points A (x1, y1) and B (x2, y2) is given by:
AB = √((x₂ − x₁)2 + (y₂ − y₁)² )
2. Section Formula
A line-segment AB, where coordinates of A(x1, y1) and B(x2, y2), is divided internally by P(x, y) in the ratio m : n is given by:
P(x, y) = (mx₂ + nx₁ / m+n , my₂ + ny₁ / m+n )
A line-segment AB, where coordinates of A(x1, y1) and B(x2, y2), is divided externally by P(x, y) in the ratio m : n is given by:
P(x, y) = (mx₂ + nx₁ / m-n , my₂ + ny₁ / m -n )
3. Mid Point formula
A line-segment AB, where coordinates of A(x1, y1) and B(x2, y2), is divided equally by P(x, y) in the ratio 1 : 1, that is, P is the mid-point of AB, is given by:
P(x, y) = (1/2 (x2 + x1), 1/2(y2 + y1) )
4. Central Formula
If three vertices of ΔABC are A (x1, y1), B (x2, y2) and C (x3, y3), then the Centroid O (x, y) of the triangle will be:
P(x, y) = (1/3 (x2 + x1), 1/3(y2 + y1) )
5. Equation of a line
Slope intercept from {m, c = y intercept}: y = mx + c.
Slope point from {P (X1, Y1) & m}: y – y1 = m (x – x1),
Two point from {P(X1, Y1) & Q(X2, Y2)} : (Y – Y1) /( Y2 – Y1 ) = (X – X1) /( X2 – X1 )
6. Slope/ Gradient/tanΘ
If two points A (x1, y1) and B (x2, y2) lie on an inclined line-segment, then the slope [m] or gradient of the line-segment
m = Y2 – Y1 / X2 -X1 = tanθ° where θ is the angle the line makes with the x axis;
If Positive it is anti-clock wise.
If Negative it is clock wise.
Two or more points lie on a line if gradient of first segment = gradient of second part = gradient of third segment etc.
7. Conditions for two lines
Two lines of slopes m1 and m2 will be –
i) If m1 = m2, lines are parallel. Here m1 = m2 →Slopes are equal ii) If m1 × m2 = – 1, lines are perpendicular to each other. Here Slopes are negative reciprocal of each other.
Reflection:
• Mx (x, y) = (x, -y)
• My (x, y) = (-x, y)
• Mo (x, y) = (-x, -y)
• X- axis: y = 0
• Y- axis : x = 0
• Any point that remains unaltered under a given transformation is called an invariant point.

More Coordinate Geometry:

Equation of a Line:
• Every straight line can be represented by a linear equation.
• Any point, which satisfies the equation of a line, lies on that line.
• Inclination of a line is the angle θ which the part of the line makes with x-axis.
• Inclination θ is positive in anti-clockwise direction and negative in clockwise direction.
• Slope or gradient of any inclined plane is ratio of vertical rise and horizontal distane.
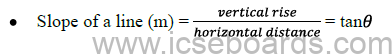
• Inclination θ of x-axis and every line parallel to it is 0.
• Inclination θ of y-axis and every line parallel to it is 90.
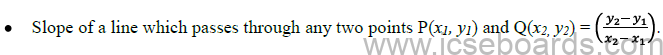
• Slopes of two parallel lines are equal or m1 = m2.
• Product of the slopes of two perpendicular line = – 1 or m1 X m2 = -1.
• Equation of a line:

Geometry
a) Similarity of triangle
If two triangles are similar then, ratio of their sides are equal.
i.e. if Δ ABC ~ΔDEF then AB/DE = BC/EF = AC/DF
Ratio of area of two triangles, ΔABC and ΔDEF is given by
Area of Δ ABC / Area of ΔDEF = AB2 /DE2 = BC2 /EF2 = CA2/DF2
Basic Proportionality theorem
If a line is drawn parallel to one side of a triangle intersecting other two sides, then it divides the two sides in the same ratio. In ΔABC, if DE || BC and intersects AB in D and AC in E then
AD / DB = AE/EC
b) Loci
It is a path traced by a moving particle which fulfills a given condition.
Types of Problems Included in syllabus
i) Constructions based on Loci.
Theorems
• Theorem 1 – The locus of a point at a fixed distance from a fixed point is a circle with the fixed point as centre and fixed distance as radius.
• Theorem 2 – The locus of a point equidistant from two intersecting lines is the bisector of the angles between the lines.
• Theorem 3 – The locus of a point equidistant from two given points is the perpendicular bisector of the line joining the points.
c) Circles
Types of Problems Included in syllabus
i) Theorems & proofs
ii) Problem based on theorem
iii) Constructions
Theorems
• The angle that an arc of a circle subtends at the center is double than which it subtends at any point on the remaining part of the circle.
• Angles in the same segment of a circle are equal (without proof).
• Angle in a semi-circle is a right angle.
• Opposite angles of a cyclic quadrilateral are supplementary.
• The exterior angle of a cyclic quadrilateral is equal to the opposite interior angle (without proof).
• The tangent at any point of a circle and the radius through the point are perpendicular to each other.
• If two circles touch, the point of contact lies on the straight line joining their centers.
• From any point outside circle two tangents can be drawn and they are equal in length.
• If two chords intersect internally or externally then the product of the lengths of the
segments are equal.
• If a chord and a tangent intersect externally, then the product of the lengths of segments of the chord is equal to the square of the length of the tangent from the point of contact to
the point of intersection.
• If a line touches a circle and from the point of contact, a chord is drawn, the angles between the tangent and the chord are respectively equal to the angles in the corresponding alternate segments.
Formulae
Assignments: r = radius of circle, C = circumference and A = area.
1. C = 2πr, where π = 22/7 and r = radius of circle
2. A = πr2, where A = area of circle
3. Area of Ring = π (R2 – r2), R = External Radius, r = Internal Radius
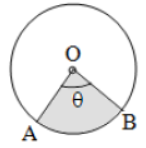
4. Area of Sector = θ/360⁰ πr2, where q = angle at center of circle. In the figure, ∠AOB = q, area is shown by shaded portion.
5. Area of Segment = Area of Sector – Area of Triangle = q
=θ/360⁰ πr2 – Area of ΔAOB, shown by shaded region.
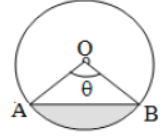
Note: If a diameter of a circle is given then find the radius first.
Symmetry:
A figure is said to have line symmetry if on folding the figure about this line, the two parts of the figure exactly coincide.
• Similarity: Criteria for similarity – 1. AA or AAA 2. SAS 3. SSS
• A drawn from vertex of a rt-<d △ divides △ the into 2 similar, also to original triangle.
• BPT – A line drawn || to any side of a △ divides other two sides proportionally.
• The areas of 2 similar △ട are proportional to the square of their corresponding sides.
• Median divides a triangle into 2 △ട of equal area.
• If △ട have common vertex & are between same ||, ratio of their areas = ratio of bases.
Loci:
• The locus is the set of all points which satisfy the given geometrical condition.
• Locus of a point equidistant from 2 fixed points is ⊥ bisector of line segment joining them.
• Locus of a point equidistant from 2 intersecting lines is angle bisector between the lines.
• Locus of a point at a constant distance from a fixed point is circle. Locus of a point equidistant from a given line is a • • pair of lines parallel to the given line and at the given distance from it.
• For equilateral triangle, centroid = incentre = circumcentre = orthocentre
Circle:
• A line drawn from centre of a circle to bisect the chord is ⊥ to the chord.
• A perpendicular line drawn to a chord from the centre of the circle bisects the chord.
• The ⊥ bisector of a chord passes through the centre of the circle.
• One and only one circle can be drawn passing through 3 non-collinear points.
• Equal chords are equidistant from the centre.
• Chords which are equidistant from the centre are equal in length.
• If the parallel chords are drawn in a circle, then the line through the midpoints of the chords passes through the centre. Greater the size of chord, lesser is its distance from the centre.
• Angle at the centre = 2 × angle on the circumference.
• Angles in the same segment are equal.
• Angle in a semicircle is a right angle
• The opposite angles of a cyclic quadrilateral are supplementary.
• If the opposite angles of a quadrilateral are supplementary, then the quadrilateral is cyclic.
• Angle in the major segment is acute and in the minor segment is obtuse.
• Exterior angle of a cyclic quadrilateral = Interior opposite angle.
• In equal or same circle. If two arcs subtend equal angle at the centre, then they are equal.
• In equal circle, if two arcs are equal, then they subtend equal angle at the centre.
• In equal circle, if two chords are equal, they cut off equal arcs.
• In equal circle, if two arcs are equal, the chords of the arcs are also equal.
• The tangent at any point of a circle & the radius through this point are ⊥ to each other.
• If two tangents are drawn to a circle from an exterior point,
o The tangents are equal,
o They subtend equal angle at the centre of the circle,
o They are equally inclined to the line joining the point and the centre of the circle.
• If two chords of a circle intersect internally/externally, the product of their segments is equal.
• Angle in the alternate segment are equal.
• Tangent2 = product of the lengths of the segments of the chord.
• Incentre – Point of intersection of the angle bisectors.
• Cicumcentre – Point of intersection of the ⊥ bisectors of the sides.
Mensuration
Types of Problems Included in syllabus:
i) Area and volumes of Cylinder
ii) Area and volumes of Cone
iii) Area and volumes of Sphere
iv) Mixed up applications
Cylinder
Formulae
Assignments: R = external radius of cylinder, r = internal radius, H = height,
1. Area of Curved Surface = 2πRH, where R = radius, H = height 2. Total Surface Area of solid cylinder = 2πRH + 2πR2
3. Volume of Solid Cylinder = πR2H
For Hollow Cylinder
1. Total Surface Area = 2πRH + 2πrh + 2π(R2 – r2)
2. Volume = πH(R2 – r2)
Sphere
Formulae
Assignments: R = external radius of sphere, r = internal radius.
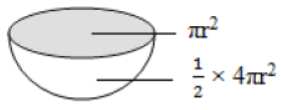
1. Curved Surface Area = 4πr2
2. Total Area of Hemi-Sphere
= 1/2 × 4πr2 + πr2
= 2πr2 + πr2
= 3πr2, shown in the figure.
3. Volume of Solid Sphere = 4/3 πr3
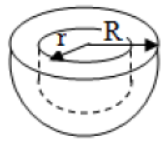
4.Volume of Hollow Sphere = 4/3π (R3 – r3)
5. Volume of Hemi-Sphere
= 1/2 × 4/3π (R3 – r3)
= 2/3π (R3 – r3), follow the figure
Cone
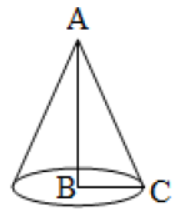
Formulae
Assignments: R = radius of cone, L = slant height, H = vertical height, shown in the figure in which slant height L = AC, vertical height H = AB and radius R = BC.
1. Area of Curved Surface = πRL
2. Total Surface Area = Area of Circular Base + Curved Surface
= πR2 + πRL = πR (R + L)
3. Volume of Cone = 1/3 πR2L
Circumference and Area of a Circle:
• Circumference of a circle = 2πr
• Circumference of a semi-circle = πr + 2r
• Circumference of a quarter-circle = 1/2 πr + 2r
• Area of a circle = πr2
• Area of a circular ring = (R2 – r2)
• Area of a semi-circle = 1/2 πr2
• Area of a quarter-circle = 1/4 πr2
• Distance travelled by a wheel in one revolution = Its circumference

Surface Area and Volume:
• Volume of a cuboid = l × b × h
• Area of 4 walls of a cuboid = 2(l + b) × h
• T.S.A. of a cuboid = 2(lb + bh + hl)
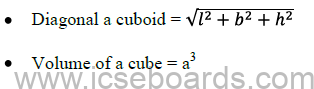
• Area of 4 walls of a cube = 4 a2
• T.S.A. of a cube = 6 a2
• Diagonal of a cube = a
• Volume of a solid cylinder = πr2h
• C.S.A. of a solid cylinder = 2πrh
• T.S.A. of a solid cylinder = 2πr(h + r)
• Volume of a hollow cylinder = π(R2 – r2)h
• T.S.A. of a hollow cylinder = 2πrh + 2πRh + 2π(R2 – r2)
• Slant height of a right circular cone, l = √h2+r2
• Volume a right circular cone = 1/3 πr2h
• C.S.A. of a right circular cone = πrl
• T.S.A. of a right circular cone = πr(l + r)
• Volume a sphere = 4/3 πr3
• Surface area a sphere = 4πr2
• Volume a hemisphere = 2/3 πr3
• Curved Surface area a hemisphere = 2πr2
• Total Surface area a hemisphere = 3πr2
• Volume a hollow sphere = 4/3 π (R3 – r3)
Trigonometry
Trigonometry:
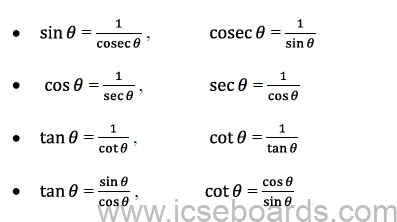
• sin2θ + cos2 = 1 (mutual understanding)
• cosec2θ – tan2θ = 1 or 1 + cot2 θ = cosec2θ (cosec is big brother)
• sec2θ – tan2θ = 1 + tan2θ = sec2θ (sec is big brother)
• ain(900 – θ) = cosθ, cos (900 – θ) = sinθ
• cosec (900 – θ) = secθ, sec(900 – θ) cosecθ
• tan (900 – θ) cotθ, cot (900 – θ) tanθ
Types of Problems Included in syllabus
i) Problem based on trigonometric identities
ii) Heights & distances
Trigonometry Identities
i) sin2 A + cos2 A = 1
ii) 1 + tan2 A = sec2 A
iii) 1+cot2 A = cosec2 A; 0 ≤ A ≤ 90°
Value of Trigonometry Identities
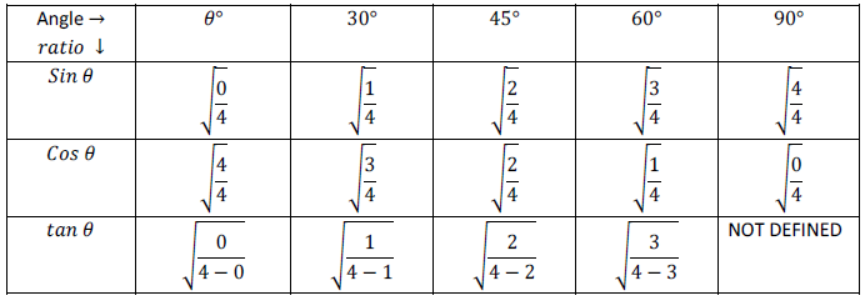
i) Sin θ= Height / Hypotenuse
ii) Cos θ = base / Hypotenuse
iii) tan θ = Height/base
iv) cot θ = base / Height
v) sec θ = Hypotenuse / base
vi) Cosec θ = Hypotenuse / Height
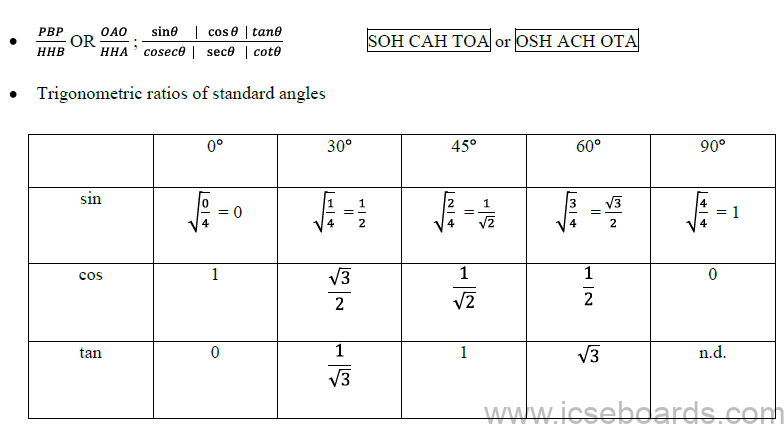
Quotient relation
i) tan θ = Sin θ / Cos θ
ii) cot θ = Cos θ / Sin θ
Formulae
1. sin2q + cos2q = 1.
2. 1 + tan2q = sec2q.
3. 1 + cot2q = cosec2q.
4. sin (90o – A) = cos A
5. cos (90o – A) = sin A
6. tan (90o – A) = cot A
7. cot (90o – A) = tan A
8. sec (90o – A) = cosec A
9. cosec (90o – A) = sec A
10. sin (180o – A) = sin A
11. cos (180o – A) = – cos A
12. tan (180o – A) = – tan A
Statistics
Statistics:

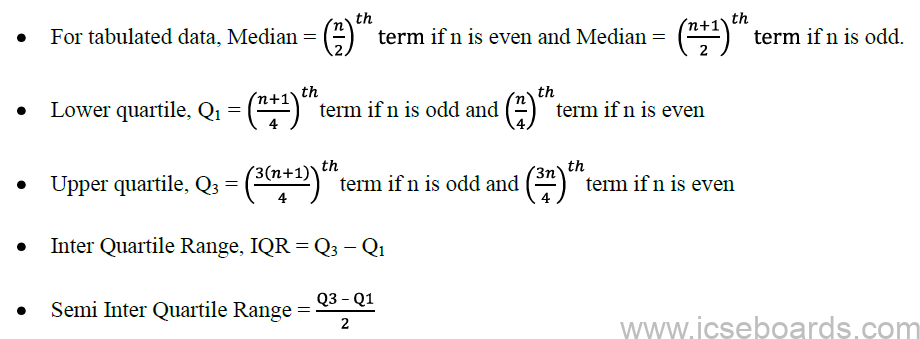
• Mode is the variate which has the maximum frequency.
• The class with maximum frequency is called the modal class.
• To estimate mode from histogram: draw two straight lines from the corners of the rectangles on either sides of the highest rectangle to the opposite corners of the highest rectangle. Through the point of intersection of the two straight lines, draw a vertical line to meet the x-axis at the point M (say). The variate at the point M is the required mode.
Types of Problems Included in syllabus
a) Computation of central tendency – Mean, Median, Mode
b) Raw & arrayed data, grouped data – both continuous and discontinuous
c) Graphical representations – Histograms & Ogives
Formulae
The arithmetic mean of numeric data x1, x2, x3, – – – , xn , where n is number of data, is given by –
Mean = x1 + x2 + x3 + ——-xn / n
Let us consider the table of (Number, Frequency) :
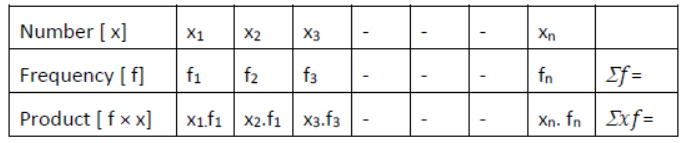
1.Mean =∑ xf /∑ f , Direct Method
2. Short-cut Method
Mean = A + ∑fd / ∑f , where A = assumed mean [mid-value of CI]
d = deviation [ x – A ]
3.Step-Deviation Method
Mean = A + ∑fu / ∑f where A = assumed mean [mid-value in x]
d = x – A, u = d/I and i = length of CI
4.Median = N +1 /2 th value, where N = odd
5. Median = Average of N/2 thand N+1/2 th value, where N = even
N/2 + N/2+1 /2 th value
6. Quartile [ Q1 ]
Q1 = L + N/4 – F /f * i,
L = lower limit of CI in N/4,
N = sum of frequencies or, last value cf,
F = preceeding value of cf,
f = value of frequency in N/4 , and i = length of CI.
7. Median [ Q2 ]
Q2 = L + N/4 – F /f * i
L = lower limit of CI in N/2,
N = sum of frequencies or, last value cf,
F = preceeding value of cf,
f = value of frequency in N/2, and i = length of CI.
8. Tertile or Upper Quartile [ Q3 ]
Q3 = L +( 2N/4 – F) /f * i
L = lower limit of CI in 3N/4,
N = sum of frequencies or, last value cf,
F = preceeding value of cf,
f = value of frequency in 3N/4, and i = length of CI.
Note: To find the median, firstly arrange the data in ‘Ascending’ or Descending’ order.
Probability:
• Probability is a measure of uncertainty.
• An Experiment is an action which results in some (well-defined) outcomes.
• Sample space is the collection of all possible outcomes of an experiment. n(S)
• An Event is a subset of the sample space associated with a random experiment. n(E)
• An Event occurs when the outcome of an experiment satisfies the condition mentioned in
• the event. The outcomes which ensure the occurrence of an event are called favourable outcomes to that event.

• The value of probability is always between 0 and 1.
• The probability of sure (certain) event is 1.
• The probability of an impossible event is 0.
• An elementary event is an event which has one (favorable) outcome from the sample space.
• A Compound event is an event which has more than one outcome from the sample space.
• If E is an event, then the event „not E‟ is complementary event of E and denoted by .
• 0≤ p(E) ≥ 1
• P(E) + P() = 1
• In a pack (deck) of playing cards, there are 52 cards which are divided into 4 suits of 13 cards each –
spades ( ♠ ), hearts ( ♥ ), diamonds ( ♦ ) and clubs ( ♣ ). Spades and clubs are black in colour, while hearts and diamonds are of red colour. The cards in each suit are ace, king, queen, jack, 10, 9, 8, 7, 6, 5, 4, 3, 2. Kings, queens and jacks are called face (picture/court) cards. The cards bearing number 10, 9, 8, 7, 6, 5, 4, 3, 2 are called numbered cards. Thus a pack of playing cards has 4 aces, 12 face cards and 36 numbered cards. The aces together with face cards (= 16). are called cards of honour.
• When a coin is tossed, it may show head (H) up or tail (T) up. Thus the outcomes are: {H, T}.
• When two coins are tossed simultaneously, then the outcomes are: {HH, HT, TH, TT}. [n(S) = 2n]
• When a die is thrown once the outcomes are: {1, 2, 3, 4, 5, 6}. [n(S) = 6n]
• When two dice are thrown simultaneously, then the outcomes are: {(1, 1),(1, 2)…….(6, 6)}.
Types of Problems Included in syllabus
i) Random experiments
ii) Sample Space
iii) Events
iv) Simple problems on single events
Probability
The mathematical theory of probability has its roots in attempts to analyze games of chance by Gerolamo Cardano in the 16thcentury, and by Pierre de Fermat and Blaise Pascal in the
17th century.
Experiment
An operation which can produce some well-defined outcomes.
Trial
Performing of an experiment.
Eg: Tossing a coin, throwing a dice
Event
The outcome of an experiment
Eg. Getting head or tail while tossing a coin
Sample Space
The set of all possible outcome in trail.
i) If one coin is tossed, the total number of outcomes are 2 i.e. Head or Tail
ii) If two coins are tossed, the total number of outcomes are 2×2=4
iii) If three coins are tossed, the total number of outcomes are 2x2x2=8
iv) In a single roll of Dice, total number of outcomes are 6
v) If two Dices are rolled, total number of outcomes are 6×6=36
Favourable case
If we toss a coin the no. of favourable cases for a head is 1
Probability
Mathematically, Probability of an event A, is defined as P(A) = No: of favorable outcomes / Total no: of possible outcome.
i) Probability = P
ii) P (certain/sure event) = 1
iii) P (impossible event) = 0
iv) All possible outcomes added = 1
Formulae
1. Probability of certain event = P(A) = No. of favourable outcomes / Total number of trials
2.Complementary Events = P(A) + P(Ā) = 1
If probability of happening of an event is x, then probability of not happening of that event = (1-x) E.g. If probability of winning a game is 0.6 then probability of losing = (1 – 0.6) = 0.4


