Students should refer to Previous Year Questions ICSE Class 10 Physics Heat with solutions that have been prepared by expert teachers of ICSE Class 10 Physics. These questions and solutions are based on past year papers that have come in examinations of ICSE Class 10. Students should understand the type of questions asked and the solutions provided. Also refer to ICSE Class 10 Physics Solutions
ICSE Class 10 Physics Heat Last Year Questions
Students should learn the important questions and answers given below for Chapter Heat in Physics for ICSE Class 10. These board questions are expected to come in the upcoming exams. Students of ICSE Class 10th should go through the board exams questions and answers for ICSE Class 10 Physics which will help them to get more marks in exams.
Board Exam Questions Heat ICSE Class 10 Physics
Previous Year Questions ICSE Class 10 Physics Heat
Short Answer Type Questions
Question: Define heat capacity and state its SI unit.
Answer: Heat Capacity of a body is defined as the amount of heat energy required to raise the temperature of
the body by 1°C. Its S.I unit is joules/kelvin
Question: Why is the base of a cooking pan generally made thick?
Answer: To increase the heat capacity of the cooking pan.
Question: A solid of mass 50 g at 150°C is placed in 100 g of water at 11°C, when the final temperature recorded is 20°C. Find the specific heat capacity of the solid. (Specific heat capacity of water = 4.2 J/g°C)
Answer: Let the specific heat capacity of solid be Cs
Given ms = 50 g Mw = 100 g
Ts = 150°C Tw = 11°C
Cs = ? Cw = 4.2 J/g°C
Final temperature = 20°C = T
Applying principal of mixtures Heat lost by hot body = Heat gained by cold body
MsCs(Ts – T) = MwCw(T – Tw)
⇒ 50 × Cs(150 – 20) = 100 × 4.2(20 – 11)
= C3 = 420 X 9 / 50 X 130
= 0.58 J/go c
Question: State two factors upon which the heat absorbed by a body depends.
Answer: (i) Directly proportional to the mass.
(ii) Directly proportional to change in temperature.
(iii) Directly proportional to the specific heat capacity.
Question: Calculate the mass of ice required to lower the temperature of 300 g of water at 40°C to water at 0°C.
(Specific latent heat of ice = 330 J/g, Specific heat capacity of water = 4.2 J/g°C)
Answer: M × 336 = 300 × 4.2 × 40
M = 300 X 4.2 X 40 / 336
= 150g
Question: What do you understand by the following statements :
(i) The heat capacity of the body is 60 JK-1.
(ii) The specific heat capacity of lead is 130 Jkg-1K-1.
Answer: (i) 60 J of heat energy is required to raise the temperature of a body by 1K.
(ii) Lead requires 130 J of heat energy to raise the temperature of 1 Kg by 1K.
Question: Rishi is surprised when he sees water boiling at 115°C in a container. Give reasons as to why water
can boil at the above temperature.
Answer: Because of the presence of impurity. (salt) More the impurity more will be the boiling point.
Question: 50 g of metal piece at 27°C requires 2400 J of heat energy so as to attain a temperature of 327°C,
calculate the specific heat capacity of the metal.
Answer: Given, Mass, m = 50 g
Δt = 327°C – 27°C = 300°C
Heat Q = 2400 J
As we know that
Q = mcΔt

Question: Define the term heat capacity and state its SI unit.
Answer: The total amount of heat required to raise the temperature of a body by 1°C is called heat capacity.
Its SI unit is J/g°C.
Question: Differentiate between heat capacity and specific heat capacity.
Answer: Specific heat capacity is defined for the unit mass of a body, whereas heat capacity is defined for entire
mass of the body.
Question: A hot solid of mass 60 g at 100°C is placed in 150 g of water at 20°C. The final steady temperature
recorded is 25°C. Calculate the specific heat capacity of the solid. (Specific heat capacity of water = 4200 J kg-1 °C-1)
Answer: According to principle of calorimeter,
Heat gained = Heat lost
So, heat gained = 150 × 4.2 × (25 – 20) …(i)
Heat lost = 60 × c × (100 – 25) …(ii)
So, From Eqs. (i) and (ii), we get
60 × c × 75 = 150 × 4.2 × 5

Question: Differentiate between heat and temperature.
Answer: Differences between heat and temperature are given below :

Question: Define calorimetry.
Answer: It is the principle through which we can understand that heat flows from higher temperature to lower
temperature and heat lost by a body is equal to the heat gained by another body when kept in contact.
Question: 200 g of hot water at 80°C is added to 300 g of cold water at 10°C. Calculate the final temperature of the mixture of water. Consider the heat taken by the container to be negligible. (Specific heat capacity of water is
4200 J kg-1 °C-1)
Answer: As given in question and from principle of calorimetry, Heat lost by hot water = Heat gained by cold water
So, 200 × 4.2 × (80 – T) = 300 × 4.2 × (T – 10)
Where, T is final temperature
⇒ 2(80 – T) = 3(T – 10)
160 – 2T = 3T – 30
⇒ 5T = 190
⇒ T = 38°C
Question: (i) Give one example, where high specific heat capacity of water is used as a heat reservoir.
(ii) Give one example, where high specific heat capacity of water is used for cooling purposes.
Answer: (i) High specific heat capacity of water is used in hot water bottles for fermentation.
(ii) High specific heat capacity of water is used for cooling radiators in cars.
Question: 40 g of water at 60°C is poured into a vessel containing 50 g of water at 20°C. The final
temperature recorded is 30°C. Calculate the thermal capacity of the vessel.
(Take specific heat capacity of water as 4.2 Jg-1 °C-1).
Answer: As from principle of calorimeter, Heat gained = Heat lost
So, Heat lost by hot water = Heat gained by cold
water + Heat gained by vessel
⇒ 40 × 4.2 × 30 = 50 × 4.2 × 10 + (Heat capacity × 10)
⇒ Heat capacity = (40 4.2 30) (50 4.2 10) / 10
= 294 J/°C
Question: Some hot water was added to three times its mass of cold water at 10°C and the resulting temperature
was found to be 20°C. What was the temperature of the hot water?
Answer: Let mass of hot water be m kg, so mass of cold
water will be = 3 m kg
Let temperature of hot water is t°C So, by principle of calorimetry
Heat taken by cold water = Heat given by hot water
mcΔt = 3 mcΔt
⇒ m × c × (t – 20) = 3 m × c × (20 – 10)
⇒ t – 20 = 3 × 10
⇒ t = 50°C
Question: Give two reasons, why copper is preferred over other metals for making calorimeter?
Answer: The two factor by which copper is preferred for calorimeter are as
(i) It has low specific heat than other metals.
(ii) It takes least amount of heat from its contents to attain the temperature of the contents.
Question: (i) Does land cool at a slower or faster rate than water? Give one reason.
(ii) Explain, why steam pipes warm a building more effectively than hot water pipes in cold countries?
Answer: (i) Because water has high specific heat capacity (4200 J/kg°C), so land cools faster than water.
(ii) As steam loses considerable amount of heat and converts into hot water. So, steam pipes warm a building more effectively in colder countries.
Question: (i) A thermometer shows a certain, temperature on its scale. When its bulb covered with a piece of cloth, soaked in spirit, it is observed that the reading of the thermometer decreases. Give reason for this observation.
(ii) It is desired to increase the rate of evaporation of a given quantity of a liquid. Suggest two ways, excluding the direct heating of the liquid, which can be used to bring about this increase in the rate of evaporation.
Answer: (i) Spirit is known to evaporate very quickly.
Each unit mass of it needs an amount of heat, equal to its specific latent heat of vaporization, during its evaporation. Hence, when the bulb of a thermometer is covered with a piece of cloth soaked in spirit, the required heat is withdrawn from the bulb of the thermometer itself. Therefore, it cools down and this results in a decrease in its reading.
(ii) We can increase the rate of evaporation of the liquid by
(a) Increasing its surface area, i.e., by spreading it out over a larger area.
(b) Increasing the motion of the air around it. This can be done, for example, by ‘putting on’ the fan over the liquid.
Question: A central heating system has radiator pipes into which steam enters at 100°C and water leaves at
100°C. Can this system succeed in heating a room? If `yes’, please explain the reason for your answer.
Answer: The system can be used for heating purposes. This is because each kilogram of steam, upon condensation into water, releases an amount of heat equal to the specific latent heat of vaporization of water. Hence, the condensing steam will release a large amount of heat into the room and this will help to heat up to room.
Short Answer Type Questions II
Question: (i) How is the transference of heat energy by radiation prevented in a calorimeter?
(ii) You have a choice of three metals A, B and C, of specific heat capacities 900 Jkg-1oC-1, 380 Jkg-1oC-1 and 460 Jkg-1oC-1 respectively, to make a calorimeter. Which material will you select ? Justify your answer.
Answer: (i) By making inner surface of calorimeter shining
(ii) Material B (380 J/kg°C) Low specific heat capacity minimize the error in calculations.
Question: (i) What is the principle of method of mixtures?
(ii) What is the other name given to it?
(iii) Name the law on which the principle is based.
Answer: (i) According to principle of mixtures, heat lost by a hot body is always equal to the heat gained by a cold body provided no heat is lost to the surroundings.
(ii) Principle of Calorimetry
(iii) Law of conservation of energy
Question: Specific heat capacity of substance A is 3.8 J/gK, whereas the specific heat capacity of substance
B is 0.4 J/gK.
(i) Which of the two is good conductors of heat?
(ii) How is one led to the above conclusion?
(iii) If substances A and B are liquid, then which one would be more useful in car radiators?
Answer: (i) As the specific heat capacity of B is much less than A, so B is good conductor of heat.
(ii) Since the specific heat capacity of B is less than A. So, B is good conductor of heat.
(iii) Since the specific heat capacity of A is higher than that of B, so it can absorb more heat
therefore, it is useful in car radiators
Question: How is the heat capacity of the body related to its specific heat capacity?
Answer: Heat capacity (Q) of body is related as follows :
Q = mcΔt
(c = specific heat capacity, m = mass of body, Δt = change in temperature)
Question: A certain amount of heat Q will warm 1 g of material X by 3°C and 1 g of material Y by 4°C. Which
material has a higher specific heat capacity?
Answer: As we know that,

So, material X has a higher specific heat capacity than Y.
Question: (i) Name the liquid which has the highest specific heat capacity.
(ii) Name two factors on which the heat absorbed or given out by a body depends.
(iii) An equal quantity of heat is supplied to two substances A and B. The substance A shows a
greater rise in temperature. What can you say about the heat capacity of A as compared to that of B?
Answer: (i) Water has highest specific heat capacity.
(ii) Factors on which heat given out or absorbed depends upon
(a) Temperature of the body with respect to surroundings.
(b) Specific heat capacity of the body.
(iii) As substance A has greater rise in temperature, so heat capacity of A is less than heat capacity of B.
Question: (i) What is the principle of method of mixtures?
(ii) Name the law on which this principle is based.
Answer: (i) The principle of method of mixture is heat gained by a cold body is equal to heat lost by hot body.
(ii) The name of this principle is principle of calorimetry.
Question: (i) Define heat capacity of a given body. What is its SI unit?
(ii) What is the relation between heat capacity and specific heat capacity of a substance?
Answer: (i) Refer Q. 1. (2 marks)
(ii) The relation between specific heat capacity and heat capacity is
⇒ Heat capacity = mass × specific heat capacity
Question: Explain, why water is used in hot water bottles for fomentation and also as a universal coolant?
Answer: Since water has large specific heat capacity, so it is used hot water bottles for fomentation. Water
is used as a universal coolant, because it has large specific heat capacity. So, that it can absorb large amount of heat.
Question: Water falls from a height of 50 m. Calculate the temperature of water, when it strikes the bottom.
(g = 10 ms-2; specific heat capacity of water = 4200 J/kg°C)
Answer: From energy conservation
Heat energy = Potential energy
mcΔt = mgh ⇒ cΔt = gh

Question: (i) Define specific heat capacity of a substance. State its SI unit.
(ii) Give one example of each, where high specific heat capacity of water is used
1. In cooling 2. As heat resistor.
Answer: (i) It can be defined as the total amount of heat
required to raise the temperature of unit mass
of substance by 1°C.
Its SI unit is J/kg°C.
(ii) 1. Water is used as coolant.
2. Heat resistor is used in car radiators.
Long Answer Type Questions
Question: (i) Name the radiations which are absorbed by greenhouse gases in the earth’s atmosphere.
(ii) A radiation X is focused by a particular device on the bulb of a thermometer and mercury in the thermometer shows a rapid increase. Name the radiation X.
(iii) Name two factors on which the heat energy liberated by a body depends.
Answer: (i) Infrared Radiations
(ii) Infrared / Microwaves / Heat Radiations
(iii) Temperature, surface area.
Question: (i) Water in lakes and ponds do not freeze at once in cold countries. Give a reason in support
of your answer.
(ii) What is the principle of Calorimetry?
(iii) Name the law on which this principle is based.
(iv) State the effect of an increase of impurities on the melting point of ice.
Answer: (i) This is because the specific latent heat of fusion of ice is sufficiently high (336 J/g), so the freeze water, a large quantity of heat has to be withdrawn, hence it freezes slowly.
(ii) If the system is fully insulated then Heat energy lost by the Hot body = Heat energy gained by the Cold body.
(iii) Law of conservation of energy.
(iv) Increase of impurity decreases the m.pt. of ice.
Question: A copper vessel of mass 100 g contains 150 of water at 50°C. How much ice is needed to cool it to 5°C?
Given : Specific heat capacity of copper = 0.4 J g-1 °C-1
Specific heat capacity of water = 4.2 J g-1 °C-1
Specific latent heat of fusion of ice = 336 J g-1
Answer: m c θ + m c θ = mIL + mi c θ
100 × 0.4 × 45 + 150 × 4.2 × 45 = mi (336 + 4.2 × 5)
mi = 84.45 g
Question: A calorimeter of mass 50 and specific heat capacity 0.42 J g-1oC-1 contains some mass of water at 20°C.
A metal piece of mass 20 g at 100°C is dropped into the calorimeter. After stirring, the final temperature of the mixture is found to be 22°C . Find the mass of water used in the calorimeter. (Take specify heat capacity of the metal piece = 0.3 J g-1oC-1, specific heat capacity of water = 4.2 J g-1oC-1.)
Answer: As from the Question
Amount of heat given by metal = mcΔT1
= 20 × 0.3 × (100 – 22) = 468 J
Amount of heat gained by water
= mw × cw × Δt2
= mw × 4.2 × (22 – 20) = 8.4 mw J
According to principle of calorimetry
8.4 mw = 468
mw = 468 / 8.4
= 50.7 g
Question: In a laboratory experiment to measure specific heat capacity of copper, 0.02 kg of water at 70°C was poured into a copper calorimeter with a stirrer of mass 0.16 kg initially at 15°C. After stirring, the final temperature reached to 45°C. Specific heat of water is taken as 4200J/kg°C
(i) What is the quantity of heat released per kg of water per 1°C fall in temperature?
(ii) Calculate the heat energy released by water in the experiment in cooling from 70°C to 45°C.
(iii) Assuming that the heat released by water is entirely used to raise the temperature of calorimeter from 15°C to 45°C calculate the specific heat capacity of copper.
Answer: (i) Quantity of heat released per kg of water per °C fall in temperature is given by 42000 J/kg°C.
(ii) Quantity of water released on cooling is given
by Q = mcΔt
⇒ Q = 0.02 × 4200 × 25 J
= 21000 J
(iii) By assuming no loss of heat by principle of calorimetry
Heat gained = Heat taken up by calorimeter
So, 2100 J = 0.16 × s × 30
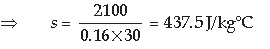
Question: A piece of iron of mass 2.0 kg has a thermal capacity of 996 J/°C.
(i) How much heat is needed to warm it by 15 °C?
(ii) What is its specific heat capacity in SI unit?
Answer: As given in question mass, m = 2 kg
Thermal capacity = 996 J/°C
Rise in temperature, Δt = 15°C
(i) Thermal capacity = Heat required / Δt
So, heat required = 966 × 15 = 14490 J
(ii) As we know, specific heat capacity

Latent Heat
Short Answer Type Questions I
Question: Give the harmful effects of global warming on lakes and oceans found frozen during winter.
Answer: Effect of global warming on lakes and oceans found frozen during winter are following
(i) Water will be evaporated due to which there will be disturbance in aquatic lift.
(ii) Disappearance of fresh and marine fishers.
Question: (i) Name a gas caused by the greenhouse effect.
(ii) Which property of water makes it an effective coolant?
Answer: (i) CO2, water vapours. Methane, and chloroform carbons.
(ii) Water has high specify heat capacity / specific
heat capacity of water is 4200 J kg-1 K-1
Question: How much heat energy is released, when 5 g of water at 20°C change to ice at 0°C
Answer: Given, m = 5 g, Δt = T2 – T1
= 20° – 0° = 20°C
c = 4.2 × 103 J/kg/°C, L = 336 J/g
So according to the question
Q – mcΔt + mL = m[(4.2 × 20) + 336]
= 5 × (84 + 336) = 2100 J
Question: Explain, why the weather becomes very cold after a hailstorm?
Sol. After the hailstorm the ice balls begin to melt and require 336 J of heat energy per gram to melt which
is taken from the atmosphere thereby, decreasing the temperature of atmosphere.
Question: Calculate the amount of heat released when 5.0 g of water at 20°C is changed into ice at 0°C. (specific
heat capacity of water = 4.2 J/g°C, specific latent heat of fusion of ice = 336 J/g)
Answer: Amount of heat released during the conversion of
5 g of water at 20°C to 5 g of ice at 0°C is as following
5 g water at 20°C to 5 g water at 0°C
= mcΔt = 5 × 4.2 × (20 – 0) = 84 × 5 = 420 J
5 g water at 0°C to 5 g ice at 0°C = mL
= 5 × 336 = 1680
So, total heat released is = 1680 + 420 = 2100 J
Question: Why does the temperature of the surrounding start falling, when the ice of a frozen lake start melting?
Answer: When frozen lakes starts melting, it takes the amount of energy per gram, equal to the latent heat
from surrounding. So there is fall in temperature of surrounding.
Question: Calculate the heat energy that will be released, when 5.0 kg of steam at 100°C condenses to form water at 100°C. Express your answer in SI unit.
(Specific latent heat of vaporization of steam is 2268 kJ/kg.
Answer: As given in question Mass, m = 5 kg
Latent heat, L = 2268 J/kg
As we know that
Q = ml
Q = 5 × 2268 = 11340 J
Question: Explain, why one feels ice cream at 0°C colder than water at 0°C?
Answer: Ice cream at 0°C extracts heat (latent heat of fusion) and freeze to water at 0°C. Ice cream is able to
extract more heat, so it produces more cooling effect.
Question: Why do pieces of ice added to a drink, cool it much faster than ice cold water.
Answer: Due to extra latent heat of fusion of ice i.e., 336 J/g each gram of ice take 336 J of extra heat from drink.
The soft drinks cool much after in ice as compared in cold water.
Question: Why are burns caused by steam more severe more than those caused by boiling water at the same temperature?
Answer: As the latent heat of vaporisation is more than specific heat of boiling water so, burn caused by
steam are more painful than boiling water.
Short Answer Type Questions II
Question: Calculate the mass of ice needed to cool 150 g of water contained in a calorimeter of mass 50 g at
32°C such that the final temperature is 5°C. Specific heat capacity of calorimeter = 0.4 J/g°C Specific heat capacity of water = 4.2 J/g°C Latent heat capacity of ice = 330 J/g
Answer: Heat gained by cold body = Heat lost by hot body
Heat gained by ice = Heat lost by water &
calorimeter
MIce × LIce + mwcw(T – 0) = mwcw(Tw – t) + mcce(Tw – T)
m × 330 + m × 4.2 × 5 = 150 × 4.2 × 27 + 50 × 0.4 × 27
⇒ 330 m + 22 m = 17010 + 540
⇒ m = 17550 / 352
⇒ 49.85 gm
Question; Calculate the amount of heat given out while 400 g of water at 30°C is cooled and converted into ice at -2 °C. Specific heat capacity of water = 4200 J/kg K Specific heat capacity of ice = 2100 J/kg K Specific latent heat of fusion of ice = 336000 J/kg
Answer: The amount of head given out on reducing the
temp of 400 g of water from 30°C to 0°C = msΔt

Total heat given out in three stages = 50,400 + 1,34,400 + 1,680
= 1,86,480 J.
Question: A body of mass “m1” of a substance of specific head capacity c1, at a temperature t1 is mixed
with another body of mass “m2” of specific head capacity “c2” at a lower temperature t2. Deduce an
expression for the temperature of the mixture t3.
Answer: Heat is lost by body at higher temperature
Heat lost = msΔt
= m1c1 (t1 – t3)
Heat will be gained by body at lower temperature.
Heat gained = msΔt
= m2c2 (t3 – t2)
According to principle of calorimetry, Heat lost = Heat gained
m1c1 (t1 – t3) = m2c2 (t3 – t2)
m1c1t1 + m2c2t2 = (m1c1 + m2c2) t3

Question: Some ice is heated at a constant rate, and its temperature is recorded after every few seconds, till
steam is formed at 10 °C. Draw a temperature time graph to represent the change. Label the two phase changes
in your graph.
Answer:

Question: It is observed that the temperature of the surrounding starts falling, when the ice in a frozen lake starts melting? Give a reason for the observation.
Sol. During the conversion of ice to water a large amount of heat is required. So, this heat is taken from the surrounding environment. As a result temperature of surrounding falls.
Question: (i) Write an expression for the heat energy liberated by a hot body.
(ii) Some heat is provided to a body to raise its temperature by 25°C. What will be the corresponding rise in temperature of the body as shown on the kelvin scale?
(iii) What happens to the average kinetic energy of the molecules as ice melts at 0°C?
Answer: (i) As from the question,
ΔQ = mcΔt
where, m = mass of substance,
c = specific heat of substance,
Δt = change in temperature,
ΔQ = heat given or lost
(ii) The temperature rise will be same in both Celsius and Kelvin scale, as it is the change in temp (Δt) only.
(iii) The average KE of molecules increases when ice melts as temperature of body increases.
Question: A piece of ice at 0°C is heated at a constant rate and its temperature recorded at regular intervals
till steam is formed at 100°C. Draw a temperature time graph to represent the change in phase. Label
the different parts of your graph.
Answer: The temperature-time graph is shown below :

Question: (i) What happens to the heat supplied to a substance, when the heat supplied causes no change in the temperature of the substance?
(ii) When 1 g of ice at 0°C melts to form 1 g of water at 0°C then, is the latent heat absorbed by the ice or given
out by it?
Answer: (i) The process is called isothermal process. Heat is stored as latent heat, which is used in changing the state of the substance.
(ii) During the melting of ice the heat given out is equal to latent heat.
Question: State in brief, the meaning of each of the following
(i) The heat capacity of body is 50 J°C-1.
(ii) The specific latent heat of fusion of ice is 336000 J kg-1.
(iii) The specific heat capacity of copper is 0.4 Jg-1°C-1.
Answer: (i) The heat capacity of body is 50 J/°C, it means 50 J of heat is required to raise the temperature
of body by 1°C.
(ii) It means this amount of heat is required to change the state of body from ice to water without change in temperature.
(iii) This means that 0.4 J of heat is required to raise the temperature of 1 g of copper by 1°C.
Question: (i) What is meant by specific heat capacity of a substance?
(ii) Why does the heat supplied to a substance during its change of state not cause any rise in its temperature?
Answer: (i) Specific heat capacity is defined as the amount of heat required to raise the temperature of
unit mass by 1°C.
(ii) Because heat supplied to the substance is used to raise the potential energy of the substance.
So, there is no change in temperature.
Question: A piece of ice is heated at a constant rate. The variation of temperature with heat input is shown in the graph here
(i) What are represented by AB and CD?
(ii) What conclusion can you draw regarding the nature of ice from the above graph?
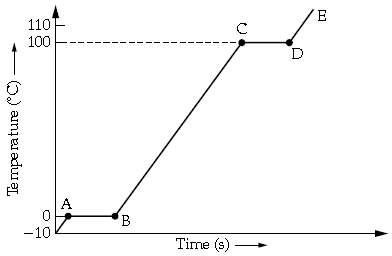
Answer: (i) As from the graph,
AB represents the time interval in which ice changes into water at 0°C.
CD represents the time in which water converts into vapour at 100°C.
(ii) As seen that initial temperature of ice is -10°C, it means there is some salt in water or it is under high pressure.
Question: (i) Define specific latent heat of vaporization of a substance.
(ii) What is the principle of calorimetry?
Answer: (i) It is the quantity of heat required to convert a unit mass of substance from liquid to vapour.
(ii) Principle of calorimetry : The heat gained by the cold body is equal to the heat lost by the hot body, provided no transfer of heat to the surroundings takes place
Long Answer Type Questions
Question: A refrigerator converts 100 g of water at 20°C to ice at -10°C in 35 minutes.
Calculate the average rate of heat extraction in terms of watts.
Given : Specific heat capacity of ice = 2.1 J g-1o C-1
Specific heat capacity of water = 4.2 J g J g-1o C–1
Specific latent heat of fusion of ice = 336 J g-1
Answer: mcθ + mL + mcθ = P × t
100 × 4.2 × 20 + 100 × 336 + 100 × 2.1 × 10 = P × 35 × 60
44100 = P × 2100
P = 21 W
Question: Heat energy is supplied at a constant rate to 100 g of ice at 0°C. The ice is converted into water at 0°C
in 2 min. How much time will be required to raise the temperature of water from 0°C to 20°C? (Given,
specific heat capacity of water = 4.2 Jg-1°C-1, latent heat of ice = 336 J/g)
Answer: As given in question,
Mass, m = 100 g,
Time, t = 2 min = 2 × 60 = 120 s
Heat energy taken by ice at 0°C to convert it into water at 0°C.
Q = mL = 100 × 336 = 33600 J As we know that

= 0.5 min
Question: 40 g of ice at 0°C is used to bring down the temperature of a certain mass of water at 60°C to 10°C. Find the mass of water used. (Specific heat capacity of water = 4200 J kg-1°C-1, specific latent heat of fusion of ice = 336 × 103 J kg-1)
Answer: As given in question,
Mass of water used, m = 40 g
Temperature of water, t1 = 0°C
L = 336 J/g, c = 4.2 J/g°C
Mass of the another water = M gram Change in temperature
Δt = (60 – 10) = 50°C
So, by principle of calorimetry Heat gained = Heat lost
⇒ M × 4.2 × (60 – 10) = (40 × 336) + 40 × 4.2 × (10 – 0)
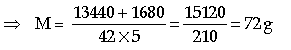
Question: 250 g of water at 30°C is present in a copper vessel of mass 50 g. Calculate the mass of ice required
to bring down the temperature of the vessel and its contents to 5°C. (Specific latent heat of fusion of ice = 336 × 103 J kg-1, specific heat capacity of copper vessel = 400 J kg-1°C-1, specific heat capacity of water = 4200 J kg-1°C-1)
Answer: According to the principle of calorimetry, Heat lost = Heat gained by water Heat gained by copper vessel
So, M × Lf = m1cwΔt = m2ccΔt

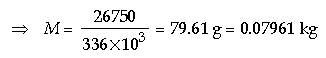
Question: (i) Define the team specific latent heat of fusion of a substance.
(ii) What energy change would you expect to take place in the molecules of a substance when it undergoes
1. A change in its temperature?
2. A change in its state without any change in its temperature?
Answer: (i) Specific latent heat of fusion is the heat required to change the state of substance from ice to liquid without change in temperature.
(ii) (a) Kinetic energy changes which defines specific heat capacity of the substance.
(b) Inter molecular or space charges defines latent heat of the substance.
Question: 50 g of ice at 0°C is added to 300 g of a liquid at 30°C. What will be the final temperature of the
mixture when all the ice has melted? The specific heat capacity of the liquid is 2.65 Jg-1°C-1, while that of water is 4.2 J g-1°C-1. (Specific latent heat of fusion of ice = 336 Jg-1)
Answer: From the question, we consider Mixture reach a final temperature = T°C
So, heat absorb by ice = mL + mc Δt
= 50 × 336 + 50 × 4.2 × T …(i)
Again heat release by liquid to come to t°C
= mcΔt
= 300 × 2.65 × (30 – T) …(ii)
According to the principle of calorimetry (Heat gained = Heat lost)
and from Eqs. (i) and (ii), we have
50 × 336 + 50 × 4.2 × T = 300 × 2.65 × (30 – T)
⇒ 1005T = 7050
⇒ T = 7.014°C
⇒ T = 7.02°C
Question: Calculate the amount of ice which is required to cool 150 g of water contained in a vessel of mass
100 g at 30°C, such that the final temperature of the mixture is 5°C. (Take specific heat capacity of material of vessel = 0.4 Jg-1°C-1, specific latent heat of fusion of ice of 336 J g-1, specific heat capacity of water = 4.2 Jg-1°C-1)
Answer: According to the principle of calorimetry,
Heat gained by ice = Heat lost by water Heat lost by vessel
⇒ mL + mcΔt = mwcwΔt + mvcvΔt
⇒ m × 336 + m × 4.2 × 5
= 150 × 4.2 × 25
100 × 4 × 25
⇒ m = 30.67 g
Question: A piece of ice of mass 40 g is dropped into 200 g of water at 50°C. Calculate the final temperature
of water after all the ice has melted. (Specific heat capacity of water = 4200 J/kg°C, specific latent heat of fusion of ice = 336 × 103 J/kg)
Answer: As given in question,
Mass of ice, mi = 40 g = 40 × 10-3 kg
Mass of water mw = 200 g
= 200 × 10-3 kg
Temperature (water) = 50°C
Let, final temperature be t. According to the principle of calorimetry Heat lost by water = Heat taken by ice
MwcDt = m,L + micDt
⇒ 200 × 10-3 × 4.2 × 103 × (50 – t)
= 40 × 10-3 × 33.6 × 10-4 + 40 × 10-3 × 4.2 × 10-3 × t
⇒ 200 × 4.2 × (500 – t) = 40 × 336 + 40 × 4.2 t
⇒ 200 × 4.2 × (500 – t) = 40 × 336 + 40 × 4.2 t
⇒ 21(50 – t) = 33.6 + 4.2 t
⇒ 25.2 t = 714
⇒ t = 28.33°C
Question: A substance is in the form of a solid at 0°C. The amount of heat added to this substance and the
temperature of the substance are plotted on the following graph

If the specific heat capacity of the solid substance is 500 J/kg°C, find from the graph
(i) The mass of the substance,
(ii) The specific latent heat of fusion of the substance in the liquid state.
Answer: (i) According to the question, Suppose, mass of substance be m kg
As we know that, Q = mcΔt from the Graph
Q = 800 J, Δt = 80°C,
c = 500 J/kg°C
⇒ 800 = m × 500 × 80

Question: If there is no heat loss to the surroundings, the heat released by the condensation of m1, gram of
steam at 100°C into water at 100°C can be used to convert m2 gram of ice at 0°C into water at 0°C.
(i) Find 1. The heat lost by steam in terms of m1. The heat gained by ice in terms of m2.
(ii) Form a heat equation to find the ratio of m2 : m1. (Specific latent heat of vaporization of steam = 2268 kJ/kg, Specific latent heat of fusion of ice = 336 kJ/kg, Specific heat capacity of water = 4200 J/kg°C)
Answer: (i) 1. The heat lost by the steam is given by m1Ls
(Ls = latent heat of steam)
2. The heat gained by the ice is given by m2Li
(Li = latent heat of ice)
(ii) According to the principle of calorimetry Heat taken by ice = Heat given by steam
m2L1 = m1Ls
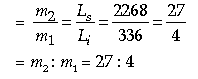
Question: (i) In winter, the weather forecast for a certain day was `severe frost’. A wise farmer watered his
fields the night before to prevent from damage to his crops. Why did he water his field?
(ii) 10125 J of heat energy boils of 4.5 g of water at 100°C to steam at 100°C. Find the specific latent heat of steam.
Answer: (i) To increase the temperature of surrounding as we know that water has high specific heat, so
it liberates very large heat when temperature falls and ice forms water.
(ii) Given, Heat Q = 10125
Mass m = 4.5 × 10-3 kg
Q = mL
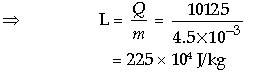
Question: A the rmoflask of negligible heat capacity contains 100 g of ice and 30 g of water.
(i) Calculate
1. The mass of steam at 100°C needed to condense in the flask to just melt the ice.
2. The amount of water in the flask after condensation.
(Specific latent heat of vaporization of steam = 2260 J/g, specific latent heat of
fusion of ice = 336 J/g, specific heat capacity of water = 4.2 J/g°C
(ii) Is it possible to condense the water formed, back to ice by adding ice at 0°C? Explain, giving a suitable reason to justify your answer.
Answer: (i) According to the principle of calorimetry Heat lost by steam = Heat gained by ice

The amount of water present after
condensation = 30 + 100 + 12.54
= 142.54 g
(ii) Water will not freeze, only ice added will melt, because water and ice used are at the same temperature.
Question: (i) State the principle of calorimetry.
(ii) Express 1 kWh in terms of SI unit of energy.
(iii) Which of the two, 1 g of ice at 0°C or 1 g of water at 0°C contains more heat? Give reason for your answer.
Answer: (i) It states that heat gained by one body is equal to heat lost by another body till they attain equal temperature.
(ii) SI unit of energy is joule (J)
i.e., 1 kWh = 1000 W × 3600 s
= 3.6 × 106 J
(iii) 1 g of water at 0°C contains more heat, because latent heat of water is 80 cal/g.
Question: In a laboratory experiment for finding specific latent heat of ice, 100 g of water at 30°C was taken in calorimeter made of copper and mass 10 g. When 10 g of ice at 0°C was added to the mixture and within the liquid till the ice melted completely, the final temperature of the mixture was found to be 20°C.
(i) What is the total quantity of water in the calorimeter at 20°C?
(ii) Specific heat capacities of water and copper being 4.2 J/g°C and 0.4 J/g°C respectively,
what quantity of heat would each release in cooling down to 20°C from the initial stage?
(iii) Write an expression for the heat gained by ice on melting.
(iv) Calculate the value of the latent heat of fusion of ice from the data discussed above.
Answer: (i) Given, m1 = 100 g, m2 = 10 g
Total mass = m1 + m2 = 100 g + 10 g
= 110 g
(ii) Total heat released = m1c1Δt + m2c2Δt
⇒ 100 × 4.2 × (30 – 20) + 10 × 0.4
× (30 – 20)
= 4200 + 40 = 4240 J
(iii) As we know, Latent heat of fusion
i.e., Q2 = mL
⇒ Q2 = 10 × L
(iv) As from the question,
10L +10 × 4.2 × (20 – 0) = 4240
So, 10L + 840 = 4240
⇒ = 10L = 4240 – 840
⇒ = L = 3400 / 10 = 340 Vg
Question: (i) It takes a much longer time to boil off (change to steam) a certain quantity of water, rather than
bring it to its boiling point from room temperature, say 25°C. Explain the reason for this.
(ii) A hot solid of mass 60 g at 100°C is placed in 100 g of water at 18°C. The final steady temperature recorded is 20°C. Find the specific heat capacity of the solid.
Answer: (i) Amount of heat required to bring water of its
boiling point = m⋅s⋅(100 – 25) = 75m cal (as s = 1
cal/g°C for water)
As we know, latent heat of steam is 540 cal/g. So, it required much longer time to boil.
(ii) Let the specific heat capacity of solid be s.
So, according to the principle of calorimetry, Heat taken by water = Heat given by solid
⇒ 100 × 1 × (20 – 18) = 60 X c X (100 – 20)
C = 100 X 2 / 60 X 80
C = 1 / 24 = 0.04 cal / g0 C
Specific heat capacity of the solid i.e., = 0.041 cal/g°C
Question: Calculate the mass of steam at 100°C that must be passed into 8.4 kg of water at 30°C to raise the temperature of water to 80°C. Specific heat capacity of water = 4.2 J/g°C. Specific latent heat of vaporization of steam = 2268 J/g.
Answer: Let the mass of steam be m gram
1. Heat given out
i.e., Latent heat of steam (Q).
mL = m × 2268 J = 2268 mJ
2. Heat given out by water = msΔ t
m × 4.2 × (100 – 80) = 84m J
∴ Total heat given out of system
= (2268m + 84m) J = 2352m J
Heat taken by 8.4 kg = msΔ t
= 8400 × 4.2 × 50°C = 1764000 J
According to the principle of calorimetry
m = 1764000 / 2352 = 750 g
Question: A jet of steam, at 100°C, is directed on to a hole drilled in a block of ice. Calculate the mass of
steam needed to melt 2 kg of ice. (Given : Specific heat capacity of water = 4200 J/kg°C; specific latent heat of fusion of ice = 336 × 103 J/kg; specific latent heat of vaporization of steam = 2268 × 103 J/kg)
Answer: Let M kg be the mass of steam needed. Now, heat given out by
(i) Steam in condensing to water at 100°C
= mass × specific latent heat
= M × 2268 × 103 J = 2268 M × 103 J.
(ii) Water at 100°C in cooling into water at 0 °C
= mass × specific heat capacity × fall in temperature
= M × 4200 × 100 = 420 M × 103 J
∴ Total heat given out by steam
= (2268 + 420) M × 103 J = 2688 M × 103 J
Also, heat needed to melt 2 kg of ice (at 0 °C)
= mass × specific latent heat of fusion
= 2 × 336 × 103 = 672 × 103 J
∴ Equating heat needed to heat given out, we get
672 × 103 = 2688 × 103 × M
M = 672 / 2688 Kg = 0.25 Kg
Question: An electric heater of 2 kW is used to heat 1 kg of ice at 0°C. All the heat is transmitted to ice.
Calculate the time needed for
(i) Ice to get converted into water at 0 °C,
(ii) Water to get heated from 0 °C to 100 °C, and
(iii) Water at 100 °C to convert itself into steam.
(Given : Specific latent heat of ice = 336000 J kg-1;
Specific heat capacity of water = 4200 J kg-1 K-1;
Specific latent heat of steam = 2260000 J kg-1)
Answer: Rate of heat energy supplied by the 2 kW electric
heater = 2000 J per second
(i) Amount of heat needed to completely melt
1 kg of ice at 0°C (specific late heat of ice) = 336000 J.
Hence, time needed = (336000/2000) second =
168 s = 2 minutes 48 second.
(ii) Amount of heat needed by 1 kg of water, at
0°C, in getting heated to 100°C = 1 × 4200 × 100 J = 420000 J
Hence, time needed = (420000/2000) second
= 210 s = 3 minutes 30 second.
(iii) Amount of heat needed by 1 kg of water at
100°C to get completely converted into steam (specific latent heat of steam) = 2260000 J
∴ Time needed is equal to (2260000/2000)
second is equal to 1130 s is equal to 18 minutes 50 seconds.
Question: A piece of metal, of mass 150 g, starts melting when heated to 800°C. On being made to solidify at the same temperature, it gives out 75000 J of heat. Find the specific latent heat of the metal. The specific heat capacity of the metal is 200 J kg-1K-1. Find the amount of heat it gives out in cooling to -50 °C?
Answer: Mass of the metal = 150 g = 150 × 10-3 kg
Heat given out on solidification at its melting point = 75000 J

Fall in temperature = [800 – (-50) °C = 850°C
Specific heat capacity = 200 Jkg-1 K-1
∴ Additional heat given out = msθ
= 150 × 10-3 × 200 × 850 J = 25500 J
Question: An object of mass 500 g is heated to a temperature of 45°C. It is put into 50 g of water of 20°C. The
final steady temperature of water becomes 25°C. Neglecting the heat taken by the container, calculate the specific heat capacity of the metal. (Given : Specific heat capacity of water = 4.2 J/(g°C)
Answer: Let s be the required specific heat capacity. Then,
Heat lost by the metal = 500 s (45 – 25)
= 10000 s units
Heat gained by the water = 50 × 4.2 × (25 – 20)
= 1050 J
By principle of calorimetry, Heat lost by metal = Heat gained by water
i.e., 10000s = 1050
s = 1050 / 10000 = 0.105 J i= I ( go C)
Question: 40 g of ice, at 0°C, is present in a vessel of negligible heat capacity. If 8 g of steam at 100°C
is passed into this ice, what is the temperature finally attained by the contents of the vessel?
(Given : Specific latent heat of vaporization of steam = 2268 J/g; Specific latent heat of fusion of ice
= 336 J/g; Specific heat capacity of water = 4.2 J/g°C)
Answer: Let θ be the final temperature of the contents of the
vessel. Heat given out by 8 g of steam (at 100°C) in
condensing into water at 100°C
= mL = 8 × 2268 J = 18144 J
Heat given out by this 8 g of water (at 100°C) in
cooling down to the final temperature of θ °C
= ms(θ1 – θ2)
= 8 × 4.2 × (100 – θ) J = 33.6 (100 – θ) J
∴ Total heat given out = [18144 + 33.6 (100 – θ) J
= (18144 + 3360 – 33.60) J
= (21504 – 33.60) J
Also,
Heat needed by 40 g of ice (at 0°C) to melt into water (at 0°C)
= mL = 40 × 336 J = 13440 J
Heat needed by this 40 g of water (at 0°C) to get heated up to the final temperature of θ °C
= ms(θ2 – θ1)
= 40 × 4.2 × (θ – 0)
= (168θ) joule
∴ Total heat taken in = (13440 + 1680) J
By the principle of calorimetry, Heat given out = Heat taken in Hence, 21504 – 33.6 θ = 13440 + 168 θ
Or 21504 – 13440 = (33.6 + 168)θ = 201.6 θ
Or 8064 = 201.60
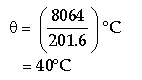
Thus, the final temperature attained by the contents of the vessel is 40°C.
Question: A 1 kW power rated electric heater was used for 120 seconds to raise the temperature of 5000 g of a given, liquid from 25°C to 31°C. What is the
(i) Heat capacity
(ii) Specific heat capacity of this liquid?
answer: Total heat supplied by the electric heater
= power of the heater × time of use
= 1000 W × 120 second = 12 × 104 W-s = 12 × 104 joule
Let c be the heat capacity of the liquid.
We have, Heat capacity = Heat required to raise its temperature through 1°C.
Now, rise in temperature = (31 – 25) °C = 6°C
∴ Heat capacity
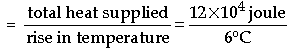
= 2 × 104 J/°C
Let s be the specific heat capacity of the liquid. We have, Specific heat capacity = heat required to raise the
temperature of a unit mass of the liquid through 1°C




