Maths Formulas for Class 10 is one of the best materials that students can get, as it will help them to concentrate better and reduce the level of stress that students face during the furious year.
Maths formulas are essential for conceptual understanding and scoring good marks, and for Revision, a list of maths formulas are always considered the best when your exams are coming. We give ICSE Maths Formulas List for Class 10 in a straightforward, free downloadable PDF design for the students to figure out a better understanding of the solutions.
On this page, we have provided Selina Maths Class 10 formulas for all chapters which are in concise mathematics class 10 book. These formulas are really important for students who are also referring to ML Aggarwal Class 10 Solutions. If students learn the maths formulas provided on this page then they will be able to solve complicated mathematics problems easily
1: Goods And Service Tax
2: Banking
3: Linear Inequations
4: Quadratic Equations
5: Ratio And Proportion
6: Remainder And Theorems
7: Matrices
8: Arithmetic Progression
9: Coordinate Geometry
10: Similarity
11: Circles
12: Mensuration
13: Trignometry
14: Statistics
15: Probability.

Maths Formulas for ICSE Class 10 Goods And Service Tax
Some Terms Related To Gst:
GST – Goods and Service Tax Before GST, there were 13 different indirect taxes in India. These 13 indirect , taxes are replaced by GST (Goods and Service Tax). GST is levised by the Central and State Government and provide for a single and streamlined process. GST is a common tax for goods and service. The tax will be implemented at every step of value creation.
CGST: The Central GST or CGST is tax collected by the Central, when the sales are within the.
SGST: The State GST or SGST is tax collected by the State, when the sales are within states. the states.
IGST: The Integrated GST or IGST is tax collected by the Central, when the sales are outside the states.
Rates of gst: The GST is levied on multiple rates from 0% to 28%. GST Council finalized a four GST tax structure of 5%, 12%, 18% and 28%. Presently Petroleum and Liquor for human consumption is exempted from GST. The GST Rates for different items are as below: IGST Rate = CGST Rate + SGST Rate.
Formula :
If output GST is more than input GST, then GST Payable = Output GST (GST on sale) – Input GST (GST on expenses purchase). If input GST is more than output GST, then GST Credit = No GST to be paid.
Maths Formulas for ICSE Class 10 Banking
Steps For Calculation of Interest :
(i) Find the minimum monthly balance on the 10th day up to the last of each month.
(ii) Add them. This is the Equivalent Monthly Principal for 1 month.
(iii) Calculate the SI on the Equivalent Monthly Principal with T = 1/12 years.
(iv) If the Amount Received on closing is asked, Add the interest to the LAST BALANCE and not to the Equivalent Monthly Principal.

2:Maturity value:P × N + I
Maths Formulas for ICSE Class 10 Linear Inequations
1.Solid circle for ≥ and ≤.
2.Hollow Circle for < and >
3.“and” means „INTERSECTION‟
4.“or” means „UNION‟.
Maths Formulas for ICSE Class 10 Quadratic Equation:
1.Steps for solving by factorization:
a.Clear all fractions and brackets if necessary.
b.Bring it to the form ax² + bx + c = 0 by transposing terms.
c.Factorize the expression by splitting the middle term as a sum of the product of a & c.

Maths Formulas for ICSE Class 10 Ratio and Proportion:
1. In the ratio, a : b, a is called antecedent and b is called consequent.
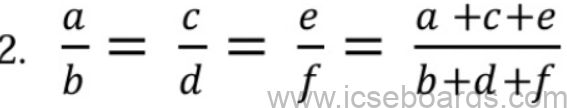
3.Compound ratio of a : b and c : d is (a X b) : (c X d)
4.Duplicate ratio of a : b is a² : b²
5.Triplicate ratio of a : b is a³ : b³
6.Sub – duplicate ratio of a : b is
√a : √b
7.Sub – triplicate ratio of a : b is
3√a : 3√b
8.Reciprocal ratio of a : b is b : a
9.Proportion – a : b : : c : d or a : b = c : d
10.Continued Proportion –
a : b : : b : c or a : b = b : c
- Invertendo – If a : b = c : d, then b : a = d : c
- Alternendo – If a : b = c : d, then a : c = b : d
- Componendo – If a : b = c : d, then a + b : b = c + d : d
- Dividendo – If a : b = c : d, then a – b : b = c – d : d
- Componendo and dividendo – If a : b = c : d, a + b : a – b = c + d : c – d .
Maths Formulas for ICSE Class 10 Remainder and Factor Theorem
- REMAINDER THEOREM: If f (x) is a polynomial, which is divided by (x–a), then the remainder is f (a).
- FACTOR THEOREM: If the remainder on dividing a polynomial f (x) by (x – a), f (a) = 0, then (x – a) is a factor of f (x).
Maths Formulas for ICSE Class 10 Matrices
1.The order of a matrix is calculated using the letter L.
2. Row matrix – Only 1 row [ a b]
3. Column matrix – Only 1 column

4. Square matrix – Number of rows =number of columns.
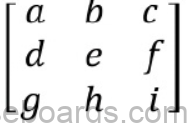
5. Rectangular matrix – The number of rows ≠ The number of columns.

Zero matrix – All elements are zero.

7. Diagonal Matrix – A square matrix with all the elements zero except the elements on the leading diagonal.

8.Unit Matrix (I) – A diagonal matrix with all the elements on the leading diagonal = 1.

9. Transpose of a matrix – If A.

10. Addition of 2 matrices

11. Multiplication of matrix by a real number – i

12. Multiplication of 2 matrices.
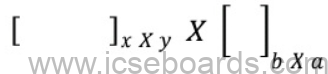
Here, y = b and the order of the product matrix = (x X a) Multiplication process:

Maths Formulas for ICSE Class 10 Arithmetic Progression
An arithmetic progression is a each term is derived from the preceding term by adding or subtracting a fixed number called the common difference “d” For example, the sequence 9, 6, 3, 0,-3,.. is an arithmetic progression with -3 as the common difference.The progression -3, 0, 3, 6, 9 is an Arithmetic Progression (AP) with 3 as the common difference.
The general form of an Arithmetic Progression is a, a + d, a + 2d, a + 3d and so on. Thus nth term of an AP series is Tn = a + (n – 1) d, where Tn nth term and a = first term. Here d = common difference = Tn – Tn-1
Sum of first n terms of an AP: S =(n/2) [2а + (n- 1)d]
The sum of n terms is also equal to the formula Sn=n/2(a+L) where 1 is the last term.
Tn = Sn- Sn-1, where Tn = nth term.
When three quantities are in AP, the middle one is called as the arithmetic mean of the other two. If a, b andc are three terms in AP then b = (a+c)/2.
Reflection
1.MX (X , Y) = (X , – Y )
2.MY(X , Y) = (– X , Y)
3.MO(X , Y) = (– X , – Y)
4.X AXIS – Y = 0;
5.Y AXIS – X = 0;
Section and Mid-Point Formula.
1. Distance formula – To find the distance between two coordinates. Distance =

2. Section formula – To find the coordinates of a point which divides the line segment with two given coordinates in a given ratio m1 : m2 Coordinates of the point (x , y)

3.Midpoint formula – To find the coordinates of the midpoint of a line segment Midpoint (x , y) =
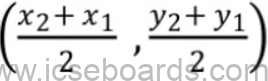
4. Centroid of a triangle – The point of intersection of the medians or the point which divides the median of a triangle in the ratio 2 : 1 from the vertex of the triangle Centroid of a triangle (x , y) =

Equation of A lines
1. Slope of a line = tan€ where € is the angle of inclination or the angle the line makes with the x axis in the positive direction.
2. Inclination € of x axis and every line || to it = 0*
3. Inclination € of y axis and every line || to it = 90*.
4. Slope of a line which passes through (x1 , y1) and (x2 , y2)

5. Slope of two parallel lines are equal.
6. Product of the slopes of two perpendicular line = – 1.
7. Equation of a line :
a. y = mx + c – Slope intercept form – where y is m is the slope and c is the y-intercept.
b. (y – y1) = m(x – x1) – Slope point form – where (x1, y1) are the coordinates of the point through which the line passes and m is the slope.
c. (y – y1) = m(x – x1) where m

-Two point form where (x1, y1) and (x2,y2) are the coordinates of the point through which the line passes.
Maths Formulas for ICSE Class 10 Similarity
1. Criteria for similarity – 1. AA or AAA criteria 2. SAS criteria 3. SSS criteria
2. A perpendicular drawn for the vertex of a right-angled triangle divides the triangle into two triangles similar to each other and also to the original triangle.
3. Basic Proportionality Theorem – A line drawn parallel to any side of a triangle divides the other two sides proportionally.
4. The areas of two similar triangles are proportional to the square on their corresponding sides.
5. Median divides a triangle into two triangles of equal area.
6. If many triangles have a common vertex and their bases are along the same straight line, the ratio between their areas is equal to the ratio between the lengths of their bases.
7. Scale factor is given by the letter k.

Maths Formulas for ICSE Class 10 Circle
1. A line drawn from the centre of a circle to bisect the chord is perpendicular to the chord.
2. A perpendicular line drawn to a chord from the centre of the circle bisects the chord.
3. The perpendicular bisector of a chord passes through the centre of the circle.
4. One and only one circle can be drawn passing through three non-collinear points.
5. Equal chords are equidistant from the centre.
6. Chords which are equidistant from the centre are equal in length.
7. If the parallel chords are drawn in a circle, then the line through the midpoints of the chords passes through the centre.
8. Greater the size of the chord, lesser is its distance from the centre.
9. Angle at the centre = 2 X Angle on the circumference
10. Angles in the same segment are equal.
11. Angle in a semicircle is a right angle.
12. The opposite angles of a cyclic quadrilateral are supplementary.
13. If the opposite angles of a quadrilateral are supplementary, then the quadrilateral is cyclic.
14. Angle in the major segment in acute and in the minor segment is obtuse.
15. Exterior angle of a cyclic quadrilateral = Interior opposite angle.
16. In equal circles or in the same circle, if two arcs subtend equal angels at the centre, then they are equal.
17. In equal circle, if two arcs are equal, then they subtend equal angles at the centre.
18. In equal circles, if two chords are equal, they cut off equal arcs.
19. In equal circle, if two arcs are equal, the chords of the arcs are also equal.
20. The tangent at any point of a circle and the radius through this point are perpendicular to each other.
21. If two tangents are drawn to a circle from an exterior point, a. The tangents are equal b. They subtend equal angles at the centre of the circle c. They are equally inclined to the line joining the point and the centre of the circle.
22. If two circles touch each other (externally or internally) the line joining the centers of the circle passes through the point of contact.
23. Direct common tangent =

24. Transverse common tangent =

25. If two chords of a circle intersect each other internally or externally, then the product of the lengths of their segments is equal.
26. Angles in the alternate segment are equal.
27. Tangent² = Product of the lengths of the segments of the chord.
28. Incentre – Point of intersection of the angular bisectors.
29. Circumcentre – Point of intersection of the perpendicular bisectors of the sides.
30. Orthocentre – Point of intersection of the altitudes .
Maths Formulas for ICSE Class 10 Mensuration
1. CIRCLE :
a.Circumference = 2πr
b.Area = πr2
2. CIRCULAR RING :
a. Area = π(R2 – r2)
3. Distance travelled by a wheel in one revolution = Its circumference.
4. No. of Revolutions =

5.CUBOID:
a.Volume = l X b X h
b. TSA = 2(lb + bh + hl)
c. Diagonal =

6.CUBE:
a.Volume = a³
b.TSA = 6a²
c.Diagonal = a_/3
7.SOLID CYLINDER:
a.Volume = πr²h
b.CSA = 2πrh
c.TSA = 2πrh + 2πr²
8.HOLLOW CYLINDER:
a.Volume = π(R² – r²)h
b.TSA = 2πRh + 2πrh + 2π(R² – r²)
9.RIGHT CIRCULAR CONE:
a.Slant height l =_/h² + r²
b.Volume = 1/3 πr²h
c.CSA = πrl
d.TSA = πrl + πr²
10.SPHERE:
a.Volume = 4/3 πr³
b. Surface area = 4πr²
11.HEMISPHERE
a.Volume = 2/3 πr²
b.Curved Surface area = 2 πr²
c.Total Surface Area = 3 πr²
12.HOLLOW SPHERE:
a.Volume = 4/3 pi(R³ – r³)
Maths Formulas for ICSE Class 10 Trigonometry
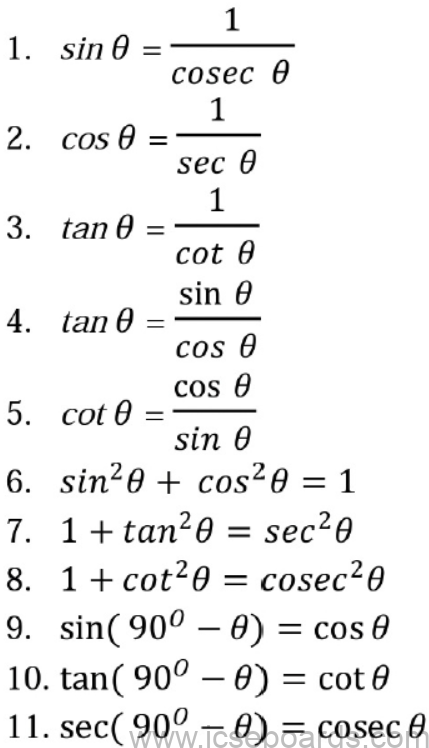
Maths Formulas for ICSE Class 10 Statistics
1. Arithmetic mean on non tabulated data

2. Arithmetic mean of tabulated data (Direct Method) :



Maths Formulas for ICSE Class 10 Probability

All Maths Formulas for Class 10 given here is ready by our Experts teachers at icseboards as per the most recent ICSE Class 10 Maths Syllabus and CISCE rules. Formulas of Maths for Class 10 will assist students with saving a ton of time during their exams.
All Maths Formulas for Class 10 PDF by icseboards are up to this point the best and most study material for ICSE Class 10 Maths.
Maths Formulas List for Class 10 will most likely increment your certainty and lessen the tension of assessment. Students can download the FREE PDF of Formulas of Maths for Class 10 and use it to clear the entirety of their questions and inquiries and henceforth, excel in their exams.


