Students should refer to Previous Year Questions ICSE Class 10 Physics Machines with solutions that have been prepared by expert teachers of ICSE Class 10 Physics. These questions and solutions are based on past year papers that have come in examinations of ICSE Class 10. Students should understand the type of questions asked and the solutions provided. Also refer to ICSE Class 10 Physics Solutions
ICSE Class 10 Physics Machines Last Year Questions
Students should learn the important questions and answers given below for Chapter Machines in Physics for ICSE Class 10. These board questions are expected to come in the upcoming exams. Students of ICSE Class 10th should go through the board exams questions and answers for ICSE Class 10 Physics which will help them to get more marks in exams.
Board Exam Questions Machines ICSE Class 10 Physics
Previous Year Questions ICSE Class 10 Physics Machines
Very Short Answer Type Questions
Question: Why is the mechanical advantage of a lever of the second order always greater than ?
Answer: The mechanical advantage of a lever of the second order is always greater than one because
its effort arm is always longer than the load arm.
Question: A scissor is a …………………………………. multiplier.
Answer: Speed.
Question: What is the principle of an ideal machine?
Answer: Principle of an ideal machine is — Work done by a machine/Work output = Work input.
Question: In what work done on ideal machine differ from a practical machine.
Answer: An ideal machine has 100% efficiency i.e., Work done on the machine = Work done by the machine. Practical machine has always efficiency less than 100%.
Question: Can a simple machine act as a force multiplier and a speed multiplier at the same time.
Answer: No
Question: Write an expression to show the relationship between mechanical advantage, velocity ratio and
efficiency for a simple machine.
Answer:

Short Answer Type Questions
Question: Why is a jack screw provided with a long arm?
Answer: Jack screw is provided with a long arm so that by applying less effort to this long arm a heavy load
can be lifted.
Question: Classify the following into levers as class I, class II, or class III:
1, A door 2. Catapult 3. Wheelbarrow 4. Fishing rod.
Answer: A door – Class II Lever.
Catapult – Class III Lever.
Wheelbarrow – Class II Lever.
Fishing rod – Class III Lever.
Question: With reference to the term mechanical advantage, velocity ratio and efficiency of a machine, name
and define the term that will not change for a machine of a given design.
Answer: (i) Velocity ratio
(ii) Ratio of velocity of effort to the velocity of load is called velocity ratio.
OR
Ratio of displacement of effort to the displacement of load in the same time is called velocity ratio.
Question: Which class of lever found in the human body is being used by a boy :
(i) When he holds a load on the palm of his hand.
(ii) When he raises the weight of the body on his toes?
Answer: (i) Class III Lever.
(ii) Class II lever.
Question: State the class of levers and the relative positions of load (L), effort (E) and fulcrum (F) in each of the
following cases :
(i) A bottle opener (ii) Sugar tongs
Answer: (i) A bottle opener : IInd class of lever, here the load L is in between the effort E and the fulcrum F .
(ii) Sugar tongs : IIIrd class of lever, here the effort of E is in between the fulcrum F and the Load L.
Question: Name a machine which can be used to
(i) Multiply force.
(ii) Change the direction of force applied.
Answer: (i) Nut cracker.
(iii) Handpump.
Question: The diagram below shows a lever in use.

(i) To which class of lever done it belong?
(ii) If FA = 40 cm. AB = 60 cm, then find the mechanical advantage of the lever.
Answer: (i) Class II lever
(iii) We know that
Load × Load arm = Effort × Effort Arm.
Mechanical advantage
=Load X EEffort arm
= ffort X Load arm
=100 / 40
2.5
Question: (i) What is meant by an ideal machine?
(ii) Write a relationship between the mechanical advantage (M.A. ) and velocity ratio (V.R.) of an ideal machine.
Answer: (i) Ideal Machine : It is a machine in which work done on the machine is equal to the work done by machine.
(ii) We know

Question: Which class of levers has a mechanical advantage always greater than one? What change can
be brought about in their lever to increase it mechanical advantage?
Answer: Class II lever have mechanical advantage always greater than one. To increase the mechanical advantage, length of effort arm must be increased and distance between fulcrum and load should be decreased.
Question: Copy the diagram of the forearm given below, indicate the positions of load , effort and fulcrum.

answer:
The diagram below shows the positions of load (L), effort (E) and fulcrum (F).

Question: What is the relationship between the mechanical Advantage and the velocity ratio for.
(i) Ideal Machine
(ii) Practical Machine
Answer: (i) For an ideal machine, the work done by the machine is equal to the work done on the machine. Therefore mechanical advantage is equal to velocity ratio
i.e., M.A. = V.R.
(ii) For practical machine, mechanical advantage is less than velocity ratio as efficiency is less than one.
M.A. < V.R.

Question: Why is mechanical advantage of a lever of third order is always less than 1? Give one example of
this class of levers.
Answer: In the third order lever, the effort E is in between the fulcrum F and the load L. The effort arm is always smaller than the load arm.

Mechanical advantage is the ratio between the effort arm and load arm so its value is always less than 1.For example : Sugar tongs
Question: What is the name given to the ratio of mechanical advantage to the velocity ratio of a machine?
When is a machine called an ideal machine?
Answer:

Hence the term given is efficiency.
A machine is called an ideal machine if its efficiency is 1 or 100%.
Question: Define the teem :
(i) Load.
(ii) Effort.
Answer: Load: The resistive force to be overcome by a machine is called load.
Effort: The force applied on machine by an external agent to enable it to work is called effort.
Question: What is the principle of lever? To which class of levers, does the balance belong?
Answer: According to principal of levers, for an ideal lever, there is no energy loss in any from;
Load × Load arm = Effort × Effort arm.
Question: Considering a simple physical balance can work as an ideal lever, what can be said about its
mechanical advantage?
Answer: For a simple physical balance, the two arm are equal in length.

Question: Find the ideal mechanical advantage of a lever in which the effort arm is 80 cm and the load arm is 5 cm.
Answer: Given, Effort arm = 80 cm
Load arm = 5 cm

Question: Draw a diagram of five tongs and mark on it the fulcrum and the point of application of load and
effort, also name the class of lever.
Answer:

Question: A nut which can be broken by applying a force of 60 kgf, is broken by using a nut cracker having its handle 15 cm long by placing it at a distance of 2 cm from the hinge. Calculate the minimum force needed to break the nut.
Answer: Load = 60 kgf
Load arm = 2 cm
Effort arm= 15 cm
We know that
Load × Load arm = Effort × Effort arm
60 × 2 = E × 15
E = 60 X 2 / 15 8kgf
Short Answer Type Questions II
Question: Define a relationship between mechanical advantage, velocity ratio and efficiency of a machine.
Answer: Work input = Effort × displacement of effort
= E × dE
Work output = Load × displacement of load
= L × dL
Efficiency = Work output / Work input
= l X dL / E X dE = (L/E)X(dLXdE)
[AsM.A. = L/E and V.R. = dEXdL]
Efficiency η = M.A./V.R.
Question: A cook uses a fine tong of length 28 cm to lift a piece of burning coal of mass 250 g. If he applies
his effort at a distance of 7 cm from the fulcrum, what is the effort in S.I. unit? (g = 10 ms-2)
Answer: Given, mass m = 250 g
= 0.25 kg
Load, L = mg = 0.25 × 10 = 2.5 N
Load arm Ld = 28 cm = 0.28 m
Effort arm (Ed) = 7 cm = 0.07 m
According to principle of Levers,
Load × Load arm = Effort × Effort arm
2.5 × 0.28 = E × 0.07
⇒ E = 10 N
Question: A pair of scissors and a pair of pliers belong to the same class of levers.
(i) Which one has mechanical advantage less than one?
(ii) State the usefulness of such a machine where mechanical advantage is less than 1.
Answer: (i) A pair of scissors has mechanical advantage less than one because the blades are longer than the handles which is used to nut a paper.
(ii) Usefulness of such a machine is to gain in speed i.e., blades move longer on paper or cloth when the handles are moved a little.
Question: State the positions of the fulcrum, load and effort for a lever of class I, II and III.
Answer: Class I lever

Question: State the class of lever to which each one of the following items belongs. Also give the relative
position of load (L), effort (E), and fulcrum (F) in each case
(i) Sea saw
(ii) Sugar tongs
(iii) Nut cracker
Answer: (i) Sea saw is a lever of class I here F lies between L and E.
(ii) Sugar tongs are a lever of class III. Here E lies between F and L.
(iii) A nutcracker is a lever of class II here L lies in between F and E.
Question: In the given figure find the effort required to balance the arm horizontal.
Answer:

In the given figure,
Load = 100 N
Load arm = (2 + 1) m = 3 m
Effort arm = 2 m
Applying principle of levers.
Effort × Effort arm = Load × Load arm
Effort × 2 = 100 × 3
⇒ Effort = 300 / 2
= 150 N
Question: A long rod of length 200 cm has its fulcrum situated at a distance of 25 cm from the load.
Calculate the mechanical advantage of the rod.
Answer:

Hence mechanical advantage = 7
Question: A rod, 4 m long is pivoted at a distance of 50 cm from its tip what is the weight of the longest stone
that can be lifted by this rod by applying an effort of 100 N?
Answer: For lifting heavy load effort arm should be longer
than load arm should be longer than load arm.
∴ Effort arm = (400 – 50)
= 350 cm
Load arm = 50 cm
Applying principle of levers
Load × Load arm = Effort × Effort arm
Load × 50 = 100 × 350
Load = 700 N
Question: A pair of scissors is used to cut a piece of a cloth by keeping it at a distance of 10 cm from its rivet
and applying an effort of 20 kgf by fingers at a distance of 4 cm from the rivet. Find :
(i) The mechanical advantage of scissors
(ii) The load offered by the cloth
(iii) How do the pair of scissors act as a force
multiplier or as a speed multiplier.
Answer: Here, Effort = 20 cm
Effort arm = 4 cm
Load arm = 10 cm
(i) Mechanical advantage = Effort arm / Load arm
M.A. 4/10 = 0.4
(ii) M.A. = Load / Effort
⇒ 0.4 = Load/20 kgf
⇒ Load = 0.4 × 20
= 8 kgf
(iii) Speed Multiplier.
Question: A man uses a crowbar of length 2 cm to raise a load of 80 kgf by putting a sharp edge below the bar at a
distance of 1.5 m from his hand. draw the diagram showing positions of load, effort and fulcrum. Also calculate mechanical advantage and effort needed?
Answer:

Pulley Systems
Very Short Answer Type Question
Question: Name the type of single pulley that has a mechanical advantage greater than one?
Answer: Single movable pulley.
Short Answer Type Questions I
Question: A pulley system has there pulleys. A load of 120 N is overcome by applying an effort of 50 N.
Calculate the mechanical advantage and efficiency of this system.
Answer: M.A. = Load/Effort
= 120 / 50
= 2.4
V.R. = 3
Efficiency, η = M.A. / V.R. X 100
η = 2.4 / 3 X 100
= 80%
Question: Draw a diagram to show how a single pulley can be used so as to have its ideal M.A. = 2
Answer:

Question: A type of single pulley is very often used as a machine even though it does not give any gain in
mechanical advantage.
(i) Name the type of pulley used.
(ii) For what purpose is such a pulley used?
Answer: (i) Single fixed pulley.
(ii) To change the direction of application of effort to a convenient direction as in case of drawing water from well.
Question: A woman draws water from a well using a fixed pulley. The mass of the bucket and water together
is 6 kg. The force applied by the woman is 70 N. Calculate the mechanical advantage. (take g = 10 ms-2)
Answer: Given,
Load, L = mg
= 6 × 10
= 60 N
Effort, E = 70 N
Mechanical Advantage M.A. = Load / Effort
M.A = 60 / 70 = 0.857
Question: Give two reasons why the efficiency of a single movable pulley system is not 100%.
Answer: A single movable pulley has an efficiency of less than 100% because
(i) The weight of movable pulley and its frame is not zero.
(ii) There is a force of friction between pulley wheel and the string.
(iii) The string used is not perfectly elastic.
Question: (i) What is the velocity ratio of a single fixed pulley?
(ii) In a single fixed pulley, if the effort moves by a distance x downwards, by what height is the load raised upwards?
Answer: (i) V.R. = 1
(ii) x
Question: (i) What is the velocity ratio of a single movable pulley?
(ii) In a single movable pulley, if the effort moves by a distance x upwards, by what height is the load raised?
Answer: (i) V.R. = 2
(ii) x / 2
Short Answer Type Questions II
Question: A boy uses a single fixed pulley to lift a load of 50 kgf to same height. Another boy uses a single movable pulley to lift the same load to the same height compare the effort applied by them. Give a reason to support your answer.
Answer: In case of single fixed pulley :
M.A. = 1
M.A. = Load / Effort
∴ 1 = 50 kgf / Effort
⇒ Effort1 = 50 kgf
In case of single movable pulley :
M.A. = 2
2 = 50 kgf / Effort2
⇒ Effort2 = 50 kgf / 2
Effort2 = 25 kgf
Effort1 / Effort2 = 50 kgf 2 / 25 kgf 1
Question: From the diagram given below, answer the questions that follow :
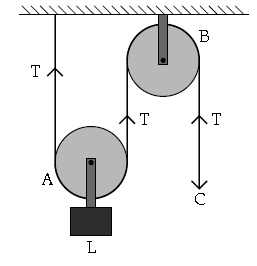
(i) What kind of pulleys are A and B?
(ii) State the purpose of pulley B.
(iii) What effort has to be applied at C to just raise the load L = 20 kgf?
(Neglect the weight of pulley A and friction).
Answer: (i) A is movable pulley
B is a fixed pulley.
(ii) So as to apply the effort in a convenient direction that is vertically downwards.
(iii) M.A. = 2 = 20 / E
Therefore, E = 10 kgf.
Question: A pulley system comprises two pulleys, one fixed and the other movable.
(i) Draw labelled diagram of the arrangement and show clearly the directions of all the forces acting on it.
(ii) What change can be made in the movable pulley of this system to increase the mechanical advantage of the system;?
Answer:

(ii) To increase the mechanical advantage of the system we reduce the friction between the string and the movable pulley. Also take the movable pulley as light as possible.
Question: A pulley system has a velocity ratio of 4 and an efficiency of 90% calculate.
(i) The mechanical advantage of the system.
(ii) The effort required to raise a load of 300 N by the system.
answer: (i) Given, Velocity ratio, V.R. = 4

Question: Name the type of single pulley that can act as a force multiplier. Draw a labelled diagram of the
above named pulley.
answer: The single pulley that can act as a force multiplier is single movable pulley.
The labelled diagram of single movable pulley is as follows :

where, E = Effort = T
L = Load = 2T
Question: A system of 5 pulleys is arranged to form a block and tackle set up. Show on a diagram, the manner
in which the string is around over this system of pulley. Also indicate the points where the load
is suspended and where the effort in applied. An effort applied to this system is used to raise the
load through 60 cm. Find the value of the distance over which the effort has moved.

Answer: Here, pulleys are there in block and tackle system.
∴ Velocity ratio = 5

Question: A load M = 200 kg is supported in two different ways shown in the given figure. F1 and F2 are the
forces needed in two cases. Calculate F1/F2.


Answer: Here, M = 200 kg
Mg = 200 × 10
= 2000 N
In first case, 2T1 = 2000 N
⇒ T1 = 1000 N
∴ F1 = 1000 N
In Second case, 2T2 = 2000 N
⇒ T2 = 1000 N
∴ F2 = 1000 N
Here F1/F2 = 1
Long Answer Type Questions
Question: A pulley system with V.R. = 4 is used to lift a load of 175 kgf through a vertical height of 15 m. The
effort required is 50 kgf in the downward direction. (g = 10 N/kg)
Calculate :
(i) Distance moved by the effort.
(ii) Work done by the effort.
(iii) M.A. of the pulley system.
(iv) Efficiency of the pulley system.
Answer:

(ii) Work done by the effort = Force × displacement
= 50 × 10 × 60 = 30,000 J.
(iii) M.A. = Load / Effort = 175 / 50 = 3.5
(iv) Efficiency, η = M.A. / V.R. = 3.5 / 4
= 0.875
= 87.5%
Question: A block and tackle system has V.R. = 5
(i) Draw a neat labelled diagram of a system including the direction of its load and effort.
(ii) Rohan exerts a pull of 150 kgf. What is the maximum load he can raise with this pulley system if its efficiency = 75%
Answer: (i) Correct diagram drawn with directions of load and effort shown correctly
(ii) Efficiency = M.A / V.R
75 / 100 = M.A / 5 M.A = 3.75
M.A = Load / Effort
3.75 = Load / 1500 or 3.75 = Load / 150
Load = 5625 N or Load / 562.50 kgf
Detailed Answer :

(ii) Effort = 150 kgf
Efficiency = 75% = 0.75
Efficiency = M.A / V.R.
⇒ 0.75 = M.A / 5
∴ M.A. = 5 × 0.75 = 3.75
M.A. = Load / Effort = 3.75 = Load / 150
⇒ Load = 150 × 3.75 = 562.5 kgf
Question; A pulley system has a velocity ratio 5. Draw a neat labelled diagram of the pulley system to lift a load
by applying the effort in a convenient direction. Mark the tension in your diagram.
(i) If the efficiency of the system is 80%, find its mechanical advantage.
(ii) If a load of 10 kgf is pulled up by a distance of 2 m in 10 s, calculate the power developed by
the effort (given g = 10 ms-2).
Answer:
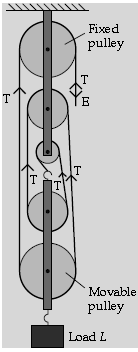
(i) V.R = 5, n = 80% = 0.80
M.A = V.R × n
= 5 × 0.8
= 4
(ii) L = 10 kgf
∴ M.A = L / e
⇒ 4 = 10 kgf / e
⇒ e = 10 / 4 = 2.5 kgf
distance travelled by effort
dE = dL × V.R.
= 2.5 = 10 m
∴ Work done by effort
W = 2.5 × 10 × 10 Joule
∴ Power = 250 J / 10s =25 Watts
Question: A block and tackle system of pulley has a velocity ratio 4.
(i) Draw a labelled diagram of the system indicating clearly the points of application and direction, of load and effort.
(ii) What is the value of the mechanical advantage of the given pulley system if 529 it is an ideal pulley system?
Answer:

(ii) Given
V.R. = 4
Load = 4T
Effort = T
M.A. = Load / Effort
= 4T / T
= 4
Question: (i) Draw a labelled diagram of a block and tackle system of pulley with two pulley in each block. Including the direction of the load, effort and tension in the string.
(ii) Write down the relation between the load and the effort of the pulley system.
Answer:

(ii) Here, load L is supported by four string
L = 4T
Effort E = T
Therefore Load / Effort = 4T / 4 =T
Load = 4 × effort
Question: A block and tackle pulley system has velocity
ratio 3 (i) Draw a labelled diagram of this system. In your diagram indicate clearly the points of
application and the directions of the load and effort.
(ii) Why should the lower block of this pulley system be of negligible weight
Answer:

(ii) Let the weight of lower block and pulley be w
Therefore L + w = 3 T
= L = 3 T – w
Effort, E = T
∴ M.A. = Load / Effort = 3T – W / T
∴ M.A. = 3 – W / T
It is clear from the expression of M.A., for higher value of mechanical advantage w should be low as possible.


