Students should refer to Previous Year Questions ICSE Class 10 Physics Work Energy And Power with solutions that have been prepared by expert teachers of ICSE Class 10 Physics. These questions and solutions are based on past year papers that have come in examinations of ICSE Class 10. Students should understand the type of questions asked and the solutions provided. Also refer to ICSE Class 10 Physics Solutions
ICSE Class 10 Physics Work Energy And Power Last Year Questions
Students should learn the important questions and answers given below for Chapter Work Energy And Power in Physics for ICSE Class 10. These board questions are expected to come in the upcoming exams. Students of ICSE Class 10th should go through the board exams questions and answers for ICSE Class 10 Physics which will help them to get more marks in exams.
Board Exam Questions Work Energy And Power ICSE Class 10 Physics
Previous Year Questions ICSE Class 10 Physics Work Energy And Power
Very Short Answer Type Questions
Question: 1 kWh = _ J
Answer: 3.6 X 106
Question: A coolie carrying a load on his head and moving on a frictionless horizontal platform does no work. Explain the reason, why?
Answer: The angle between the applied force and the displacement of load is 90°.
W = Fscos θ = Fscos 90° = 0
Question: How is work done related to the applied force?
Answer: Work done = Force applied × displacement
Question: Define work.
Answer: Work is said to be done if on applying a force a body gets displaced through a finite displacement.
Question: Define energy and state its unit.
Answer: Energy is the capacity to do work. Its S.I. unit is joule.
Short Answer Type Questions I
Question: A Boy weighing 40 kg climbs up a stair of 30 steps each 20 cm high in 4 minutes and a girl weighing
30 kgs does the same in 3 minutes . Compare
(i) The work done by them.
(ii) The power developed by them.
Answer: Total height gained = 30 X 20 / 100 = 6 m
(i) Work done by the boy = 40 × 10 × 6 = 2400 J
Work done by the girl = 30 × 10 × 6 = 1800 J
Therefore, ratio = 2400 : 1800 = 4 : 3
(ii) Power of boy = 2400 / 4 X 60 = 10 W
Power of girl = 1800 / 3× 60 = 10 W
Ratio = 10 : 10= 1 : 1
Question: How is work done by a force measured when the force :
(i) is in the direction of displacement.
(ii) is at an angle to the direction of displacement.
Answer: (i) W = F × s
(ii) W = F × s cos q
Where q is the angle between force and displacement.
Question: Explain briefly why the work done by a fielder when he takes a catch in a cricket match is negative.
Answer: Force exerted on the ball and the displacement of the ball are in opposite directions or they make 180° with one another.
Detailed Answer :
The angle between force applied by the fielder and the displacement of ball is 180°
∴ W = Fscos 180° [cos 180 = -1.]
= – Fs
∴ Work done is negative
Question: (i) When does a force do work?
(ii) What is the work done by the moon when it revolves around the earth?
Answer: (i) When the applied force produces displacement in the direction of the force.
(ii) Zero.
Question: Calculate the change in the kinetic energy of a moving body if its velocity is reduced to 1/3rd of the initial velocity?
Answer: K.E.1 : K.E.2
= 1 / 2 × m × (1)2 : 1 / 2 × m × (1 / 3)2
= 1 : 1/9
= 9 : 1
Detailed Answer :
Let initial velocity = 3v
and final velocity = v
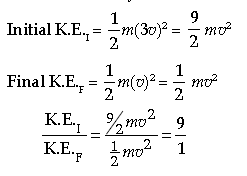
Question: A man having a box on his head, climb up a slope and another man having an identical box walks the same distance on a levelled road. Who does more work against the force of gravity and why?
Answer: Man climbing up the slope, because he has to work against the force of gravity, whereas for the man moving on the levelled road, work done = 0 because displacement is normal to the force of gravity.
Question: A body is thrown vertically upwards. Its velocity keeps on decreasing. What happens to its kinetic energy as its velocity becomes zero?
Answer: As the velocity decreases, kinetic energy decreases but height increases. Hence potential energy increases. At the highest point, velocity becomes zero, kinetic energy becomes zero and is completely converted into potential energy.
Question: A force is applied on a body of mass 20 kg moving with a velocity of 40 m/s. The body attains a velocity of 50 m/s in 2 sec. Calculate the work done by the body.
Answer: Mass, m = 20 kg
Initial velocity, u = 40 m/s
Final velocity, v = 50 m/s
Applying work-energy theorem
W = 1 / 2 m (v2 – u2)
W = 1 / 2 X 20[(50)2 – (40)2]
= 10 X [2500 – 1600]
= 10 X 900
= 9000 J
.
Question: A body is acted upon by a force. State two conditions under which the work done could be zero.
Answer: The two conditions under which the work done can be zero are as :
(i) Displacement is zero.
(ii) Angle between the force and displacement is 90°.
Question: State the amount of work done by an object, when it moves in a circular path for one complete
rotation. Give your reason to justify your answer.
Answer: Work done = Force × displacement Here after one complete revolution, displacement is zero.
∴ Work done = zero
Question: What should the angle between forces and displacement be to get the
(i) Minimum work?
(ii) Maximum work?
Answer: (i) θ = 90°.
Here W = Fscos 90° [cos 90° = 0]
∴ W = 0 [minimum work]
(ii) θ = 0°.
W = Fscos 0 [cos 90° = 0]
W = Fs [maximum work
Question: What is kinetic energy? Give two examples of bodies possessing kinetic energy.
Answer: Kinetic Energy : The energy possessed by a body by virtue of its motion is called kinetic energy. Examples are
(i) A moving train.
(ii) A running boy.
Question: When is the potential energy of an oscillating simple pendulum
(i) maximum and
(ii) minimum
Answer: (i) The potential energy of a simple pendulum is maximum when its bob is at extreme position
(ii) The potential energy is minimum when bob is at its mean position.
Question: Give the S.I. unit of energy other than the S.I. unit, what are the two other units of energy?
Answer: The S.I. unit of energy is joule. Other two units of energy are
(i) electron volt (eV)
(ii) kilowatt hour (kWh)
Question: Compare the kinetic energy of a car of mass m moving with velocity 80 km/hr and a truck of mass
2 m moving with velocity 40 km/hr.
Answer:
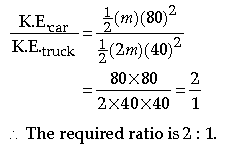
Question: A given force displaces an object through a distance s in its own direction and then in a
direction inclined at 60° to its own direction. What is the ratio of the work done in the two cases?
Answer: Work done = Fscos θ
Case I : θ = 0
⇒ W1 = Fscos 0°
W1 = Fs
Case II : W2 = Fscos 60° [as θ = 60°]

Question: What is the value of the total energy of a body at any instant, after it is allowed to fall from a height of 10 m? The mass of the body is 2 kg. (g = 9.8 m/s2)
Answer: Potential energy of the body when it is at a height of 10 m is
P = mgh
= 2 × 9.8 × 10
= 196 J
Total energy of body remains conserved. Hence total energy at any instant is 196 J.
Question: The speed of a body is reduced to half of its original value. By what factor does this changes the kinetic energy of the body?
Answer:
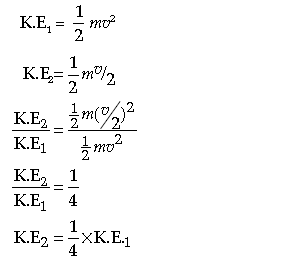
Thus kinetic energy of body decreases by a factor of 4.
Question: Write S.I. unit of work. How is it related to electron volt?
Answer: S.I. unit of work is joule.
1 eV = 1.6 × 10-19 joules.
Question: When an arrow is shot from a bow it has kinetic energy in it. Explain briefly from where it gets its kinetic energy.
Answer: When the bow is stretched elastic potential energy gets stored in it. When the arrow is released this elastic potential energy of bow gets converted into kinetic energy of the arrow.
Question: Two bodies, A and B of equal mass are kept at heights 20 m and 30 m respectively. Calculate the
ratio of their potential energies.
Answer: Let mass of each body = m
∴ Potential energy of A, PA= mg (20)
Similarly potential energy of B, PB= mg (30)
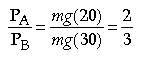
Question: A body of mass 5 kg is moving with a velocity of 10 ms. What will be the ratio of its initial kinetic
energy and final kinetic energy, if the mass of the body is doubled and its velocity is halved?
Answer: Here, m1 = 5 kg
v1 = 10 ms-1
m2 = 10 kg
v2 = 5 ms-1
K.E.1 = 1 / 2 × 5 × (10)2 = 250 J
K.E.2 = 1 / 2 × 10 × (5)2 = 125 J
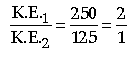
Question: A spring is kept compressed by a small trolley of mass 0.5 kg lying on a smooth horizontal surface
as shown in the figure given below :
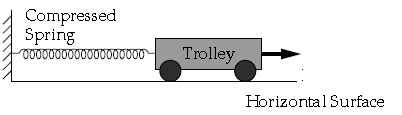
When the trolley is released, it is found to move at a speed of 2 ms-1. What potential energy did the spring posses when compressed?
Answer: Given, mass of trolley m = 0.5 kg
Final velocity of trolley v = 2 ms-1
∴ Kinetic energy of trolley = 1 / 2 mv2
= 1 / 2 X 0.5 × 2 × 2
= 1 J
According to law of conservation of energy the potential energy of the compressed spring is converted to the kinetic energy of the moving trolley.
∴ Potential energy of compressed spring = 1 J
Question: A ball of mass 200 g falls from a height of 5 m. What will be its kinetic energy when it just reaches the ground? (g = 9.8 ms-2)
Answer: Given, m = 200 g = 200 / 1000 kg
∴ m = 1 / 5 kg.
Height, h = 5 m
∴ Potential energy of ball at a height of 5 m is
P.E. = mgh
= 1 / 5 X 9.8 × 5
= 9.8 J.
According to law of conservation of energy the kinetic energy of ball just before striking the ground is 9.8 J.
Question: (i) State the principle of conservation of energy.
(ii) Name the form of energy which a body may posses even when it is not in motion.
Answer: (i) “Energy can neither be created nor be destroyed but be transferred from one form to another.”
(ii) Potential Energy.
Question: A ball is placed on a compressed spring. When the spring is released the ball is observed to fly away.
(i) What form of energy does the compressed spring posses?
(ii) Why does the ball fly away?
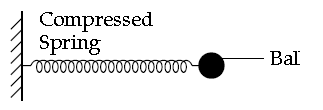
Answer: (i) Elastic potential energy.
(ii) The potential energy stored in compressed spring gets converted into kinetic energy of the ball. Hence ball flies away.
Question: A body of mass 0.2 kg falls from a height of 10 m to a height of 6 m above the ground. Find the loss in potential energy taking place in the body. (g = 10 ms-2)
Answer: Mass, m = 0.2 kg
Initial height, h1 = 10 m
final height, h2 = 6 m
P.E.1 = 0.2 × 10 × 10 = 20 J
P.E.2 = 0.2 × 10 × 6 = 12 J
∴ Loss in potential energy = (20 – 12) J
= 8 J
Question: A moving body weighing 400 N possesses 500 J of kinetic energy. Calculate the velocity with which
the body is moving. (g = 10 m/s2)
Answer: Weight of body = 400 N
Let mass of body = m kg
⇒ mg = 400
⇒ m × 10 = 400
⇒ m = 40 kg
Given, kinetic energy = 500 J Let its velocity be v m/s
∴ 1 / 2 mv2 = 500 J
⇒ 1 / 2 × 40 × v2 = 500
⇒ v2 = 500 / 20
⇒ v2 = 25
⇒ v = 5 ms-1
Question: State work energy theorem. Give its mathematical expression also.
Answer: According to the work energy theorem, the work done by a force on a moving body is equal to the
increase in its kinetic energy.
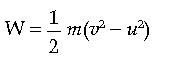
Question: Derive a relationship between kinetic energy and momentum of a moving body.
Answer: Let a body of mass m be moving with a velocity v m/s.
Momentum, P = mv
Kinetic energy, K = 1 / 2 mv2
⇒ K = m2v2 / 2m
⇒ K = (mv)2 / 2m
⇒ K = P2 / 2m
⇒ P2 = 2 mk
Question: Calculate the kinetic energy of a body of mass 0.11 kg and momentum 20 kg ms-1.
Answer: Given, m = 0.1 kg
And P = 20 kg ms-1
We know that K = P2 / 2m
∴ Kinetic energy = 20 X 20 / 2 X 0.1
Kinetic energy = 2000 J.
Question: A body is dropped from a height h above the ground. Draw a graph showing variation of both kinetic energy and potential energy with height.
Answer:
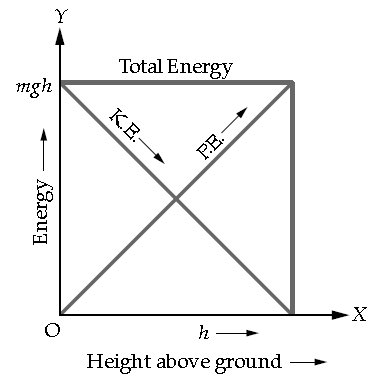
Question: The bob of a simple pendulum is imparted a velocity of 5 ms-1 when it is at its mean position.
To what maximum height (vertical) will it rise on reaching to its extreme position? (g = 10 ms-2)
Answer: Let mass of bob = m kg
Velocity at mean position = 5 m/s Kinetic energy of bob at its mean position
K = 1 / 2 m (5)2
Let the vertical height reached = 1 m
According to law of conservation of energy
K.E.mean position = P.E.extreme position
⇒ 1 / 2 m × 25 = mgh
⇒ 25 / 2 = 10 × h
⇒ h = 25 / 20
⇒ h = 1.25 m
Short Answer Type Questions II
Question: Draw a diagram to show the energy changes in an oscillating simple pendulum. Indicate in your
diagram how the total mechanical energy in it remains constant during the oscillation.
Answer:
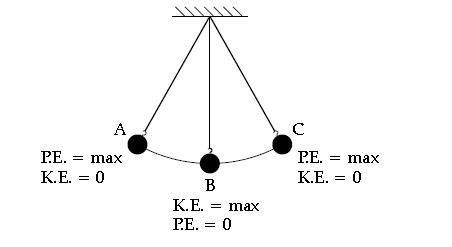
Question: A body of mass 50 kg has a momentum of 3000 kg ms-1. Calculate :
(i) the kinetic energy of the body.
(ii) the velocity of the body.
Answer: (i) m = 50 kg
Momentum P = 3000 kgms-1
P = mv
⇒ v = P / m 3000 / 50 = 60 ms-1
Kinetic energy of the body = 1 / 2 mv2
= 1 / 2 X 50 X 60 X 60
= 90,000 J.
(ii) Velocity of body, v = 60 m/s
Alternate method :
Given, m = 50 kg
P = 3000 kg ms-1
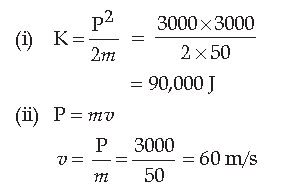
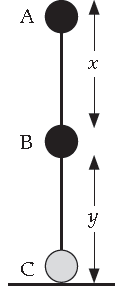
Question: An object of mass ‘m’ is allowed to fall freely from a point A as shown in the figure. Calculate the total mechanical energy of object at :
(i) Point A
(ii) Point B
(iii) State the law which is verified by your calculations.
Answer: (i) Total energy at A = mg(x + y)
(ii) Total energy at B = mg(x + y)
(iii) Law of conservation of mechanical energy.
Question: Define ‘joule’ the S.I. unit of work and establish a relationship between the S.I. and C.G.S. units of work.
Answer: Joule : 1 joule of work is said to be done when a force of 1 N displaces a body through 1 metre in its own direction.
1 J = 1 N × 1 m
= 105 dyne × 100 cm
= 107 dyne × cm
1 J = 107 erg.
Question: (i) Define a kilowatt. How is it related to the joule?
(ii) How can the work done be measured when force is applied at an angle to the direction of displacement?
Answer: (i) One kilowatt hour is the electrical energy consumed by at electrical appliance of power 1 kilowatt when it is used for one hour.
1 kWh = 3.6 × 106 J
(ii) Work = F × scos θ
where, θ = angle between force and displacement.
Power and Sources of Energy
Very Short Answer Type Questions
Question: The conversion of part of the energy into an undesirable form is called _____________
Answer: Degradation of energy.
Question: What is nuclear energy?
Answer: The energy released from the nucleus of an atom when it undergoes fission or fusion is called nuclear energy.
Question: By what factor does the kinetic energy of a moving body change when its speed is reduced to half?
Answer: KI = Initial Kinetic Energy = 1 / 2 mv2
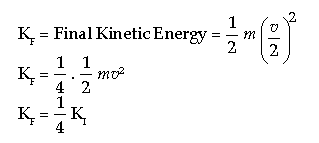
Hence kinetic energy becomes 1 / 4 th of the initial kinetic energy.
Question: What does kilowatt hour measure?
Answer: Electrical energy.
Short Answer type Questions I
Question: If the power of a motor be 100 kW, at what speed can it raise a load of 50,000 N?
Answer: Given Power, P = 100 kW
= 100 X 1000 W
Load (force), F = 50,000 N
Let the speed with which, the load is raised = v ms-1
Applying formula, P = F.v
⇒ 100 X 1000 = 50,000 X v
⇒ v = 100 X 100 X 1000 / 50,000
⇒ v = 2 ms-1
Question: State the energy changes in the following while in use :
(i) Burning of a candle.
(ii) A steam engine.
Answer: (i) Chemical energy to light energy and heat energy.
(ii) Chemical energy to heat energy and the chemical energy.
Question: Rajan exerts a force of 150 N in pulling a cart at a constant speed of 10 ms-1. Calculate the power exerted.
Answer: P = F × v
= 150 × 10
= 1500 W.
Question: State the energy changes in the following devices while in use :
(i) A loud speaker
(ii) A glowing electric bulb.
Answer: (i) Electrical energy to Sound Energy.
(ii) Electrical energy to heat energy to light energy.
Question: (i) State the energy conversion taking place in a solar cell.
(iii) Give one disadvantage of using a solar cell.
Answer: (i) Light energy to electric energy.
(ii) It cannot be used at night or on a cloudy day.
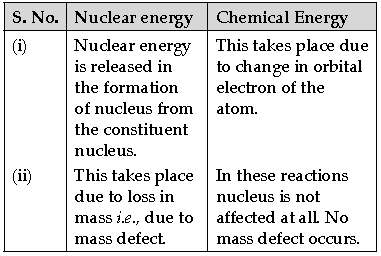
Question: Mention any two differences between nuclear energy and chemical energy.
Answer:
Question: What is the main energy transformation that occurs in :
(i) Photosynthesis in green leaves.
(ii) Charging of a battery.
Answer: (i) Light energy to chemical energy.
(iii) Electrical energy to chemical energy.
Question: State one important advantage and disadvantage each of using nuclear energy for producing electricity.
Answer: Advantage : A very small amount of nuclear fuel can produce a large amount of energy.
Disadvantage : Very harmful radiations are produced.
Question: State the energy changes that takes place in the following when they are in use
(i) a photovoltaic cell
(ii) an electromagnet
Answer: (i) Light energy to electrical energy.
(iii) Electrical energy to mechanical energy.
Question: What energy conversions take place in the following when they are working?
(i) Electrical toaster.
(ii) Microphone
Answer: (i) Electrical energy to heat energy.
(iii) Sound energy to electrical energy
Question: A ball of mass 0.2 kg is thrown vertically upwards with an initial velocity of 20 m/s. Calculate the maximum potential energy it gains as it goes up.
Answer: Given, mass m = 0.20 kg
Initial velocity, u = 20 ms-1
According to principle of conservation of energy maximum P.E. gain = Initial K.E.
P.E.max = 1 / 2 × 0.2 × (20)2
= 40 J
Question: A girl of mass 35 kg climbs up from the first floor of a building at a height 4 m above the ground to the third floor at a height 12 m above the ground. What will be the increase in her gravitational potential energy? (g = 10 ms-2)
Answer: Given, Mass, m = 35 kg
Height of first floor, h1 = 4 m
Height of third floor, h2 = 12 m
Gravitational potential energy at first floor
P.E.1 = mgh.
= 35 × 10 × 4
= 1400 J
Gravitational potential energy at third floor
P.E.2 = 35 × 10 × 12
= 4200 J
Gain in potential energy = P.E.2 – P.E.1
= 4200 – 1400
= 2800 J
Question: The work done by the heart is 1 Joule per beat. Calculate the power of the heart, if it beats 72 times in one minute.
Answer: Work done in one beat = 1 J
Work done in 72 beats = 72 J
time = t = 1 min = 60 sec
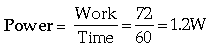
Question: If the power of a motor is 40 kW, at what speed does it raises a load of 20,000 N?
Answer: Given,
Power, P = 40 kW
= 40,000 W
Load = force = 20,000 N
Applying formula,
P = F.v
40,000 = 20,000 X v
v = 2 ms-1
Question: A machine raises a load of 750 N through a height of 16 m in 5 s. Calculate the power at which the machine works.
Answer: Given, Load, F = 750 N
Height, h = 16 m,
Time t = 5 sec

Question: A body P has a mass of 20 kg and is moving with a velocity of 5 ms-1. Another body Q has a mass of 5 kg
and is moving with a velocity of 20 ms-1. Calculate :
(i) The ratio of the momentum of P and Q.
(ii) The kinetic energy of P in S.I. units.
Answer: Given, mass of body P, mp = 20 kg
Velocity of body P, vp = 5 ms-1
Mass of body Q, mQ = 5 kg
Velocity of body Q, vQ = 20 m/s
(i) Momentum of body P, Pp = mpvp
(ii) = 20 × 5
(iii) = 100 kg ms-1
Momentum of body Q, PQ = mQvQ
= 5 × 20
= 100 kg-ms-1
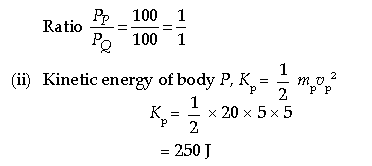
Short Answer Type Questions II
Question: An engine can pump 30,000 L of water to a vertical height of 45 m in 10 min. Calculate the work done
by the machine and the power. (Density of water = 103 kg/m3, 1000 L = 1 m3, g = 9.8 ms-2
Answer:
Sol. Given, Volume V = 30000 L = 30 m3
Height h = 45 m
Time t = 10 min = 10 × 60 = 600 s
Density of water ρ = 103 kg/m3
g = 9.8 m/s2
Work done W = ?, Power P = ?
W = mgh = Vρgh [∴m = Vρ]
30 × 103 × 9.8 × 45
= 13230 × 103 J = 1.323 × 107 J
Power P = W / t = 1.323 X 107 / 600 = 2.205 X 104 W
Question: ‘Renewable sources of energy must be encouraged to meet growing demands of energy’. Give suggestions to support your answer.
Sol. Renewable sources of energy must be encouraged to meet growing demands of energy, because of
the following
(i) It will minimise the use of conventional sources of energy which have limited stocks.
(ii) It helps to control to a large extent.
(iii) Sources of energy are inexhaustible.
Question: 6.4 kJ of energy causes a displacement of 64 m in a body in the direction of force in 2.5 seconds.
Calculate :
(i) The force applied.
(ii) Power in horse power. (1 H.P. = 746 Watts)
Answer: Given, energy, E = 6.4 kJ
= 6,400 J
Time t = 2.5 seconds
Displacement S = 64 m
(i) Energy = Work done = Force × displacement

Question: An engine can pump 30,000 L of water to a vertical height of 45 m in 10 min. Calculate the work done
by the machine and its power. (G = 9.8 m/s2) (Density of water = 103 kg/m3, 1 m3 = 1000 L)
Answer: Given, volume of water, v = 30,000 L
= 30,000 / 1000 = 30 m3
mass of water = volume × density
= 30 × 1000 kg
= 30,000 kg
Work done by the machine = mgh
= 30,000 × 9.8 × 45
= 1.323 × 107 J
Power = Work Done / Time
= 1.323 X 107 / 600
= 22.05 × 103
= 22.05 kW



