Students should refer to Heat ICSE Class 10 Physics Notes and solutions below. Our teachers have provided numerical problems and solutions for chapter Heat in ICSE Class 10 Physics. These notes are really useful if you are preparing for ICSE exams. concise physics class 10 solutions are also very important for Physics students.
ICSE Class 10 Physics Heat Numerical Problems
Students can refer to the Numerical Problems prepared for Chapter Heat in Class 10 ICSE. These notes will be really helpful for the students giving the Physics exam in ICSE Class 10. Our teachers have prepared these concept notes based on the latest ICSE syllabus and ICSE books issued for the current academic year. Please refer to Chapter wise notes for ICSE Class 10 Physics provided on our website.
Heat ICSE Class 10 Physics Revision Notes
Calorimetry
Revision Notes
➢ Heat : It is the form of energy which flows from one part to other parts of the system without any mechanical work involved (by virtue of temperature difference only). It measures the total internal energy possessed by the particles. It is represented by Q. The S.I. unit of heat is Joule (J). Another unit of heat is Calorie (cal).
➢ Temperature : It is the measure of the degree of hotness or coldness of any body. Heat flows from a body at higher temperature to a body at the lower temperature, until they reach to equal temperature. The SI unit of temperature is Kelvin (K). Other units of temperature are Celsius (°C) and Fahrenheit (F).
Temperature (in K) = 273 + temperature (in °C)
Temperature in (in F) = (Temperature (°C) × 9/5) + 32
➢ Different Units of Heat Energy : (i) One calorie : Calorie is the quantity of heat needed to raise the temperature of 1 g of water from 14.5°C to 15.5°C , i.e., through 1°C, around the mean value of 15°C or the amount of heat required to raise the temperature of 1 g of pure water by 1°C.
1 cal = 4.186 J = 4.2 J
(ii) One kilocalorie : It is the amount of heat required to raise the temperature of 1 kg of pure water by 1°C. 1 kcal = 103 cal = 4.2 × 103 J
➢ Thermal Capacity or Heat Capacity : Thermal capacity is defined as the total amount of heat required to raise the temperature of a body by 1°C (or 1K). It is represented by C.
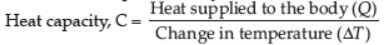
Its SI unit is J/°C or J/K.
➢ Difference between Heat and Temperature :

➢ The specific heat capacity of a substance is the amount of heat energy required to raise the temperature of unit mass of that substance through 1°C (or 1K). Its S.I. unit is J/(Kg K).
➢ Difference between Heat Capacity and Specific Heat Capacity :

➢ The amount of heat gained or lost by a substance depends on the following three factors :
(i) The rise or fall in the temperature of the substance.
(ii) The quantity or the mass of the substance taken.
(iii) The nature of substance.
➢ The supply of heat to a body generally increases the kinetic energy of its molecules, and this shows itself as a rise in the body’s temperature.
➢ Relation between thermal capacity and specific heat capacity :
Thermal capacity = mass × specific heat capacity.
➢ We may view the specific heat capacity as one of the factors on which thermal inertia of the body depends. More the specific heat capacity, more it is difficult to change the thermal state, i.e., the temperature of the body.
➢ Specific heat capacity of water = 1 cal /(g°C) = 4.2 × 103 J /(kg°C).
➢ The specific heat capacity of water is much higher than that of most of the substances. Thus, water has a high thermal inertia.
➢ According to the principle of heat transfer or principle of calorimetry :
The heat gained by the cold body is equal to the heat lost by the hot body, provided no transfer of heat to the surroundings.
➢ When m kg of a substance of specific heat capacity c is heated (or cooled) through °C, the quantity of heat Q gained (or lost) by the substance is given by
Q = mcθ
➢ The equilibrium temperature θ, during heat transfer, is given by
m1c1(θ1 – θ) = m2c2 (θ – θ2)
θ = [m1c1θ1 + m2c2θ2] / [m1c1 + m2c2]
➢ The method of mixtures—Based on the principle of heat transfer is often used for measurement of the specific heat capacity of a given body.
➢ The high value of the specific heat capacity of water finds many applications in nature and in practice. For example, due to the high specific heat of water, it is used as a coolant.
➢ SI Units :

➢ Relevant Physical Constants :
1. Specific heat capacity of water = 1 cal/(g °C) = 4.2 × 103 J /(kg °C)
2. Specific heat capacity of ice = 2100 J kg–1 K–1
3.The following table gives the values of specific heat capacities of some common substances :

Latent Heat
➢ Phase change diagram.

➢ The phenomenon of melting, freezing, boiling (evaporation) and condensation make up the subject matter of change of state.
➢ During the change of state, average kinetic energy does not change but average potential energy changes (increases on melting).
➢ The melting or fusion of crystalline solid into its corresponding liquid takes place (under given external condition) at a particular temperature known as its melting point.
➢ Melting point decreases due to the presence of impurities and increase in pressure.
➢ Specific latent heat of fusion of ice = 336 × 103 J/Kg.
➢ The heat Q needed to melt m kg of a substance of specific latent heat of fusion L, is given by Q = mL.
➢ The boiling point of a liquid, under given external conditions, is that constant temperature at which the liquid starts boiling, i.e., gets converted into the vapour state (at a very fast rate).
➢ We can explain a number of natural phenomena using the ideas of specific latent heat of fusion.
• In cold countries, water in lakes does not freeze all at once.
• Drinks get more cooler by adding ice than by ice cold water at 0°C.
• It is colder after a hail storm than before or during it.
IMPORTANT FORMULAS
1) Heat capacity = Amount of heat / Rise in temperature
Heat capacity C= Q/ΔT J /°c or J° 𝑐-1 or 𝐽𝐾-1
(ΔT = Rise or change in temperature & Q = Amount of heat)
2) Specific Heat Capacity, C = Amount of heat / Mass X Rise in temperature
C= Q/m x ΔT
J Kg-1 K-1 or J Kg-1° C or Cal g-1 ° c-1
Or Q = mc ΔT Joule
3) Heat Capacity = Mass X Specific Heat Capacity
C = mc
4) Heat Energy gained or lost
= Mass of the substance X Specific heat capacity X Change in temperature.
= mc (T2 – T1) where
m = Mass in kg, T2 = Higher temperature in ° c, T1 = Lower temperature in °c.
5) Heat lost by the hot body = Heat gained by the cold body
m1 c1((T1 – T) = m2 c2 ( T – T2)
6) Specific latent heat of a substance = Heat released or absorbed by the substance / Mass of the substance
Or L = Q/m where L = specific latent heat
Q = Quantity of heat and m = mass of the substance.
7) The amount of heat absorbed or liberated for the change of phase, Q= L x M
POINTS TO REMEMBER
1) Water has the highest specific heat capacity. i.e 4.2 J/g°c.
In other words, every 1gm of water will absorb 4.2 joules of heat energy, when its temperature rises by 1°c only.
2) Ice has the highest specific latent heat. Its experimental value is 336 X 103J kg-1 in S.I System.
3) Specific latent heat of vaporisation of steam: It is the amount of heat energy required to change 1 kg of water at 100°c, into 1 kg of steam at 100°c, without any rise in temperature. It is 226 X 104 J kg -1. Steam has the highest specific latent heat capacity of vaporization.
4) 1 calorie = 4.2 J.
5) 1 Kilocalorie = 4200 J
6) Heat → Joule
7) Specific heat capacity:
In C.G.S system → 1/g0c or Jg-1 C-1
In S.I system → 1/kgk or Jkg-1 K-1
8) Thermal capacity
In C.G.S system → J° 𝐶-1
In S.I System → 𝐽𝐾-1
9) Specific latent heat:
In C.G.S system → J 𝑔-1
In S.I system → J 𝐾𝑔-1
10) Specific latent heat of vapourisation
In C.G.S system → J 𝑔-1
In S.I system → J 𝐾𝑔-1
In old system → calories 𝑔-1
Symbols Used In Problems
H = Heat
m = Mass
C’ = Heat capacity
C or S = Specific heat capacity
L = Specific Latent heat of fusion of ice.
Δ T or = Rise or change in temperature
t or T = Final temperature
t1 = lower temperature
t1 = Higher temperature
Q = Amount of heat
P = power
IMPORTANT PROBLEMS & SOLUTIONS
1) A certain amount of heat Q will warm 1 gram of material ‘X’ by 3 degree Celsius and 1g of material ‘ Y’ by 4°c. Which material has a higher specific heat capacity?
Let CX and CY be the specific heat capacity of X and Y respectively
Then m1 CX Δ t1 = m2 CY Δ t2
1 X CX X 3 = 1 X CY X 4
3 CX = 4Cy
CX /Cy = 4/3 =Cx > Cy
Hence, Material X has the higher specific heat capacity.
2) Calculate the mass of ice required to lower the temperature of 300g of water at 40°c to water at 0°c(specific latent heat of ice = 336 J/g, Specific heat capacity of water = 4.2 J/g°c)
Let ‘m’ be the mass of ice. Heat energy required to melt to lower the temperature = m X L = m X 336
Heat energy imparted by the water in fall of its temperature from 40°c to 0 °c = mass of the water X specific heat capacity X fall in temperature = 300 X 4.2 X 40°c
If there is no loss of heat m X 336J/g = 300 g X 4.2 J/g °c X 40°c
4m = 300 X 4.2 X 400 / 336
4m = 150g.
So mass of ice required is 150g. [ANS]
3) A copper vessel of mass 100g contains 150g of water at 50°c. How much ice is needed to cool it to 5°c?
Given: Specific heat capacity of copper = 0.4 Jg-1 °c -1
Specific heat capacity of water = 4.2 Jg-1 °c -1
Specific latent heat of fusion of ice = 336 J g-1

Let mass of ice required be 𝑥
Heat gained by ice to form water at 0°c = mL = 𝑥 X 336 = 336𝑥
Heat gained by water formed from ice = mc QR =𝑥X 4.2 X 5 = 21𝑥
Total heat gained = 336𝑥 + 21 𝑥 = 357𝑥
Heat lost by water at 50° c = mc F = 150 X 4.2 X 45 = 28350 J
Heat lost by vessel at 50°c = 100 X 0.4 X 45 = 1800 J
Total heat lost = 1800 + 28350 = 30150 J.
Heat lost = Heat gained.
357𝑥 = 28350
𝑥 = 28350 /357 = 85.45g [ANS]
4) A refrigerator converts 100g of water at 20°C to ice at -10°c in 35 minutes. Calculate the average rate of heat extraction in terms of watts.
Given: Specific heat capacity of ice = 2.1 Jg-1 ° c-1
Specific heat capacity of water = 4.2 Jg-1 °c-1
Specific latent heat of fusion of ice = 336 J g-1
[ANS]According to question m= 100g, t1 = 20°C,
t2 = -10° C , T = 35 minutes = (35 X 60) sec
C Water = 42 J/g 1°c
C ice = 2.1 J/g 1°c
L = 336 J/g , P = w/t = ?
Heat drawn in cooling water from 20°c to 0°c
Δ Q1 = mc Δ t = 100 X 4.2 X 20 J
Heat drawn in converting 100gm of water at 0°c to ice at 0°c
Δ Q1 = mc Δ t
= 100 X 4.2 X 20 J
= (420 X 20) J = 8400 J
Heat drawn in converting 100g water at 0°c to ice at -1°c
ΔQ2 = mL + mc Δ t
= 100 X 336 + 100 X 2.1 X 10
= (33600 + 2100) J = 35700 J
Δ Q = Δ Q1 + Δ Q2
= (8400 + 35700) J = 44100 J
T = 35 X 60 sec = 2100 sec
The average rate of heat extraction in terms of watts
= w/t = Δ Q/t = 44100 / 2100 J/s = 21J/s
= 21 watts [ANS]
5) Heat energy is supplied at a constant rate to 100gm of ice at 0°c. The ice is converted to water at 0°c in 2 minutes. How much time is required to raise the temperature of water from 0°c to 20°c?
Given:
Sp. Heat capacity of water is 4.2 J g -1 ° c-1
Sp. Latent heat of ice = 336 Jg-1
Given m = 100g, t = 2min = 120sec.
Heat energy taken by ice at 0°c to convert to water at 0°c
Q = mL = 100 X 336 = 33600 J
4 P = Q/t = 33600 / 120 = 280 J/s
The heat energy required to convert water at 0°c to 20°c.
Q = m C Δ t = 100 X 4.2 X 20 = 8400 J.
Q = P X t
8400 = 280 X t
t= 8400 / 280 = 30sec =0.5 min
Time required to raise the temperature of water from 0°c to 20° c is 0.5 min [ANS]
6) How much heat energy is released when 5gm of water at 20°c changes to ice at 0°c?
[Sp. Heat capacity of water = 4.2 J g-1 °c -1
Sp. Latent heat of fusion of ice = 336 J g -1]
Heat energy released = mc ΔT + mL
= 5 X4.2 X 20 + 5 X 336
= 420 + 1680
= 2100 Joule [ANS]
7) 50 gram of metal piece at 27°c requires 2400° J of heat energy so as to attain a temperature of 327°c. Calculate the specific heat capacity of metal
Given m = 50g
Δt = (327-27) ° c = 300°c
Q = 2400 J
Now, Q = mc Δ t
2400 = 50 X C X 300
C = 0.16 J/g °C [ANS]
(m= mass, Δt = rise in temperature and Q = heat energy, C = specific heat capacity)
8) A hot solid of mass 60g at 100°c is placed in 150g of water at 20°c. The final steady temperature
recorded is 25°. Calculate the specific heat capacity of solid.
[Specific heat capacity of water = 4200 J kg-1 °C-1]
Heat gained by water = 150 X 4.2 X 5 (5Δt =25-20 = 5°c)
Heat lost by hot solid = 60 X C X 75 (5Δt = 100 -25 = 75°c)
By the law of mixtures, if no heat is lost to the surroundings,
Heat gained by cold water = Heat lost by hot solid.
150 X 4.2 X 5 = 60 X C X 75
Specific heat capacity of the solid,
C = 150 X 4.2 X 5 / 60 X 75
= 0.7 J g-1 ° C-1 [ANS]
9) 40g of ice at 0°c is used to bring down the temperature of a certain mass of water at 60°c to 10°c.
Find the mass of water used.
[Specific heat capacity of water = 4200 J kg-1 °C-1]
Specific latent heat of fusion of ice = 336 X 103 J Kg-1]
Let ‘M’ be the mass of water. Then, Heat lost by water = M.C. ΔT
= M X 4.2 X (60-10)
= M X 4.2 X 50 ….. [1]
Heat gained by ice = Heat gained for melting + heat gained to come to temperature 10°c
= ML + Mc Δ T
= (40 X 336) + (40 X 4.2 X 10) …. [2]
If no heat is lost to the surrounding, Heat gained by ice = Heat lost by water or M X 4.2 X 50 = (40 X
336) + 1680= 13440 + 1680= 15120
∴ M = 15120 /210 = 72 𝑔𝑚. [ANS]
10) 200g of water at 80°c is added to 300g of cold water at 10°c. Calculate the final temperature of the mixture of water. Consider the heat taken by the container to be negligible. The specific heat capacity of water is 4200 J Kg-1 °C-1.
Let the final temperature be T °c, Then, Heat lost by hot water = 0.2 X 4200 X (80-T) J
Heat gained by cold water = 0.3 X 4200 X (T – 10) J
According to the principle of mixture;
heat lost = heat gained
0.2 X 4200 X (80-T) = 0.3 X 4200 X (T-10)
= 0.2 X (80-T) = 0.3 X (T-10)
= 16 – 0.2 T = 0.3 T -3
Or 0.3 T + 0.2 T = 16 + 3
Or, 0.5 T = 19
Or T = 19 / 0.5 = 38°c
Hence the final temperature of the mixture of water is 38° c [ANS]
11) 50g of ice at 0°c is added to 300g of a liquid at 30°c. What will be the final temperature of the mixture when all the ice has melted? The specific heat capacity of the liquid is 2.65 J g-1 ° C -1 While that of water is 4.2 J g-1 ° C-1 Specific latent heat of fusion of ice = 336 J g-1.
Let ‘t’ be the final temperature then,
Heat given by liquid = Heat taken by ice to change the state + heat taken by water to increase the
temperature.
Or, 300 X 2.65 X (30- t) = (50 X 336) + (50 X 4.2) X (t-0)
Or, 23850-795 t = 16800 + 210 t
Or, 1005 t = 7050
Or, t = 7.01 °C
Hence, the final temperature of the mixture is 7.01 °c [ANS]
12) 40g of water at 60°c is poured into a vessel containing 50g of water at 20°c. The final temperature recorded in 30°c calculates the thermal capacity of the vessel. Take specific heat capacity of water
as 4.2 J g-1 °c -1.
Heat lost by water to change its temperature from 60°c to 30°c = mc Δt = 40 X 4.2 X 30 J = 5040 j
Heat gained by water = (50 X 4.2 X 10) J
According to the principle of calorimetry or, Heat gained = Heat lost 2100J + Heat of vessel = 5040J
Or, Heat of vessel = (5040-2100) J = 2940J
⸫ Heat capacity = Amount of heat / rise in temperature
= 2940 J /10 ° C = 294 𝐽 ° C-1
So thermal capacity (heat capacity) of the vessel is 294 J °C-1 [ANS]
13) A piece of ice of mass 40g is dropped into 200g of water at 50° c . Calculate the final temperature of water after all the ice has melted.(Specific heat capacity of water = 4200J/Kg °c, Specific latent heat of fusion of ice = 336 X 103 J/kg)
Let ‘t’ be the final temperature then heat given by water = m X C X Δt
= [200 X 10-3 X 4.2 X 103 (50-t)
= (42,000 – 840t) J
Heat taken by ice to change into water at 0° c = 40 X 10-3 X 336 X 103 = 13,440J
Heat taken by water to change its temperature from 0°c to t °c = (40 X 10-3 X 4.2 X 103 X t) J
= 168t J
Total heat taken by water = (13,440 +168 t) According to the principle of calorimetry.
Heat given = Heat taken
Or, 42000 – 840 t = 13440 + 168 t
Or, 840 t + 168 t = 42000 – 13440
Or, 1008t =28560
Or, t = 28.33 °c
Final temperature of water is 28.33 °c [ANS]
14) An electric heater raises the temperature of 5000g of a given liquid from 25°c to 31°c in 120 s. If the power of the heater is 1 Kw, Calculate (a) the heat capacity of the liquid. (b) The specific heat capacity of the liquid.
Let ‘s ‘be the specific heat capacity of the liquid. Heat used in raising the temperature of the liquid
from 25°c to 31°c.
= 5000 X S (31-25) J
= 5000 X S X 6 J …..[1]
Heat produced by the electric heater is 120S = 1000 watt X 120s
= 120000 J …. [2]
From 1 & 2
5000 X S X 6 = 120000 or s = 120000 / 30000 = 4 g-1 ° C-1
Heat capacity of the liquid = 5000 X 4 = 20000 J
So heat capacity of the liquid is 4 g-1 ° C-1 and specific heat capacity is 20,000J.
15) Some hot water was added to three times its mass of cold water at 10°c and the resulting temperature was found to be 20°c. What was the temperature of the hot water?
Let the temperature of the hot water be t°c and mass of hot water = m gm
Mass of cold water = 3m gm
Temperature of cold water = 10°C
Final temperature of mixture = 20°c
Heat taken by cold water = 3m X C X (20-10)
Heat given by hot water = m X C X (t-20)
Heat given = Heat taken
m X C X ( t -20) = 3m X C X 10
= t-20 = 30
⸫t = 30 + 20 = 50° C
So temperature of hot water was 50°C [ANS]
16) Calculate the heat energy that will be released when 5.0 Kg of steam at 100°c condenses to form water at 100°c. Express your answer in SI unit. (Specific latent heat of vaporization of steam is 2268 KJ Kg-1)
Heat energy released = mL
= 5.0 X 2268 = 11340 KJ
= 1134 X 104 J [ANS]
17) 10125 J of heat energy boils off 4.5g of water at 100°c to steam at 100°c, Find the specific latent heat of steam
Specific latent heat of stem is given by S=E/m = 10125/4.5 X 10-3
= 2250 X 103 J Kg-1 [ANS]
18) m1 g of steam, at 100°c, is condensed to form water at 100°c. If there is no heat loss to the surroundings, the heat released in this process is used to convert m2g of ice at 0°c into water at 0°c.
i. Find the heat lost by steam in terms of m1 and the heat gained by ice in terms of m2
ii. Form a heat equation and find the ratio of m2 : m1 from it. (Specific latent heat of vapourization
of steam= 2268 KJ Kg-1
Specific latent heat of fusion of ice = 336 KJ Kg-1
Specific heat capacity of water = 4200 J Kg -1 ° C.
i. Heat lost by steam = m1
L v
= m1 X 2268 KJ Kg-1
Heat gained by ice = m2 L f = m2X 336 KJ KG-1 [ANS]
ii. Now, heat lost by steam = heat gained by ice. m1 X 2268 = m2 X 336
Or m2: m1 = 2268 / 336 = 27:4
So the ratio is 27:4 [ANS]
19) Calculate the amount of heat released when 5.0g of water at 20°c is changed into ice at 0°c
Specific heat capacity of water = 4.2 J/g °c
Specific latent heat of fusion of ice = 336 J/g)

⸫ Amount of heat released = mc + mL
= 5 X 4.2 X (20° – 0°) + (5 X 336)
= 21.0 X 20 + 1680 = 42.0 + 1680
= 2100 Joule [ANS]
20) A piece of iron of mass 2.0 Kg has a thermal capacity of 966 J/ °C.
i. How much heat is needed to warm it by 15°c?
ii. What is its specific heat capacity in S.I units?
i. Given that: M = 2.0 Kg,
Thermal capacity = 966 J /°C and rise in temperature = 15°c
Thermal capacity, C = Heat required /rise in temp
⸫ Heat required = 966 X 15
= 14490 J [ANS]
ii. Specific heat capacity C = Amount of heat / mass x rise in temp
= 14490 /2.0 x15 = 14490 / 30
= 483 J/Kg/°C [ANS]
21) A thermos flask of negligible heat capacity contains 100g of ice and 30g of water.
a. Calculate the mass of steam at 100°c needed to condense in the flask to just melt the ice.
b. Calculate the amount of water in the flask after condensation.
Specific latent heat of vaporisation of steam=2260 J/g.
Specific latent heat of fusion of ice = 336 J/g
Specific heat capacity of water = 4.2 J/g °c
a. M (ice) X L (ice) = M(gas) X L (gas)
100 X 336 = M X 2260
Or Mass of steam, M = 100 x336 / 2260
= 14.86 gm [ANS]
b. Amount of water in the flask after condensation = mass of (water present + Melted ice + Condensed steam)
=30 + 100 + 14.86 = 144.86 gm [ANS]
22) In a laboratory experiment for finding specific latent heat of ice, 100g of water at 30° was taken in a calorimeter made of copper and of mass 10g. When 10g of ice at 0°c was added to the mixture and kept within the liquid till the ice melted completely the final temperature of the mixture was found to be 20°c.
i. What is the total quantity of water in the calorimeter at 20°c?
ii. Specific heat capacities of water and copper being 4.2 J/g °c and 0.4 J/g°C respectively, what quantity of heat would each release in cooling down to 20°c from the initial stage?
iii. Write an expression for the heat gained by ice on melting.
iv. Calculate the value of the latent heat of fusion of ice form the data discussed above.
i. Total water in calorimeter = 100g + 10g = 110g [ANS]
ii. Heat lost by water + Heat lost by calorimeter in cooling down to 20°c

= 100 X 4.2 X (30-20) + 10 X 0.4 X (30-20)
= 4200 + 40 = 4240J [ANS]
iii. Heat gained by ice = Q2= ML = (10 x L) J [ANS]
iv. 10L + 10 x 4.2 X (20-0) = 4240
10 L + 840 = 4240,
10 L = 3400
∴ L = 3400 / 10 = 340 𝐽/𝑔
So latent heat of fusion of ice is 340 J/g [ANS]
23) A vessel of negligible heat capacity contains 40g of ice in it at 0°c. 8g of steam at 100°c is passed into the ice to melt it. Find the final temperature of the contents of the vessel.
[Sp. Latent heat of vaporisation of steam = 2268 J/g.
Sp. Latent heat of fusion of ice = 336 J /g &
Specific heat capacity of water = 4.2 J/g°C]
Let ‘T be the final temperature of the contents of the vessel.
Heat given out by 8g of steam (at 100°c) in condensing into water at 100°c
= mL = 8 X 2268 J = 18144 Heat given out by this 8g of water (at 100°c) in cooling down to the final temperature of T°c.
= 8 X 4.2 X (100-T) = 33.6 X (100 – T) J
Total heat given out = [18144 + 33.6 (100-T)] J
= (18144 + 3360 – 33.6 T)
= (21504 – 33.6 T) J
Also heat needed by 40 g of ice (at 0°c) into melting into water (at 0°c) = mL = 40 X 336 J = 13440J
Heat needed by this 40g of water (at 0°c) in getting heated upto the final temperature of T°c.
= 40 X 4.2 X (T-0) = 168 T J
Total heat taken in (13440 + 168 T) J
By principle of calorimetry
Heat lost = heat gained
(21504-33.6T) j = (13440-168 T) J
Solving for T we have T = 40°C
Final temperature attained by the contents of the vessel is 40°c [ANS]
24) In a laboratory experiment to measure specific heat capacity of copper 0.02 Kg of water at 70°c was poured into a copper calorimeter with a stirrer of mass 0.16 Kg initially at 15°c. After stirring, the final temperature reached to 45°c. Specific heat of water is taken as 4200 JKg-1 ° c -1
i. What is the quantity of heat released per Kg of water per 1°c fall in temperature?
ii. Calculate the heat energy released by water in the experiment in cooling form 70 °C to 45 °c
iii. Assuming that the heat released by water is entirely used to raise the temperature of calorimeter from 15 °c to 45 °c, Calculate the specific heat capacity of copper.
i. The heat energy released by 1 kg of water per 1 °c fall in its temperature is the magnitude of the specific heat capacity of water i.e. 4200J [ANS]
ii. The heat energy H1 released by water in the experiment is given by
H1 = 0.02 X 4200 X (70-45) = 2100 J [ANS]
iii. Let H2 be the heat needed by the calorimeter + stirrer for getting heated.
Then H2 = 0.16 X S X (45-15) = 4.8 SJ
Or 4.8 S = 2100 or S = 2100/4.8
⸫ S = 437.5 J Kg-1 °C-1
Hence specific heat capacity of copper is 437.5 Jkg-1 ° C-1 [ANS]
25) A hot solid of mass 60g at 100°C is placed in 100g of water at 18°c. The final steady temperature recorded is 20°c. Find the specific heat capacity of the solid.
Heat lost by solid = mc1 θ
= 60 X C1 X 80 J
Heat gained by water = mc θ
= 100 X 4.2 X 2J
By principle of calorimetry we have heat cost = Heat gained
60 X C1 X 80 = 100 X 4.2 X 2
Solving for C1 we have C1 = 0.175 J g-1 ° C-1 [ANS]
26) Calculate the mass of steam at 100 °c that must be passed into 8.4 Kg of water at 30 °c to raise the temperature of water to 80 °c.
Let the mass of steam at 100 °c be ‘m’ g
- Heat given out by steam in condensing into water at 100 °c = ml
= m X 2268 J
= 2268 MJ - Heat given out by water at 100 °c (obtained from the condensation of steam) in cooling down to
80 °c
= m X C X t
= m X 4.2 J/g ° C X (100-80) °C
= m X 4.2 X 20 = 84 m J
Hence, total quantity of heat given out by steam.
= (2268m + 84m) J
= 2352 m J.
Heat taken up by 8.4 kg of water
= 8400 g of water in raising its temperature from 30 °c to 80 ° c i.e. by 50 °c = 8400 g X
4.2 J lg °C X 50 ° C = 1764000 J.
Since heat given out by stem = Heat taken up by water 2352 m = 1764000
⸫ m = 1764000 / 2352 g = 750g.
⸫ Mass of steam required = 750g.
27) 2 Kg of ice melts when a jet of steam at 100 °c is passed through a hole drilled in a block of ice. What mass of steam was used?
Given:
Specific heat capacity of water = 4200 J/Kg °C
Specific latent heat of fusion of ice = 336 X 103 J/Kg.
Specific latent heat of vaporisation of steam = 2268 X 103 J /Kg.
Let ‘m’ Kg of steam be required
Heat given out by steam to condense into water at 100 °c=mL.
= m (2,268 X 103) J
Heat given out by m Kg of water so cool from 100 °c to 0 °c
= mc ΔT
= m X 4200 J/Kg °c X (100-0) °C
= m X 42 X 104 J
Total heat lost = m (2268 X 103) + m (42 X 104)
= m X 2688 X 103 J.
Heat gained by 2 kg of ice in melting at 0 °c
= 2 X (336 X 103) J = 672 X 103 J.
Heat lost = Heat gained
4 m X 2688 X 103 = 672 X 103
Or m = 672 x 103 / 2688 x 103
Or, m= 0.25 Kg.
4 0.25 Kg of steam was used [ANS]
28) 10g of ice at 0 °c absorbed 5460 J of heat to melt and change into water at 50 °c. Calculate the specific latent heat of fusion of ice. Given specific heat capacity of water is 4200 J Kg-1 ° C-1
Quantity of heat required to melt ice = 10 X L
Quantity of heat required to raise the temperature from 0 °C to 50 °C = 10 X 4.2 X 50
According to the question 5460 = 10 X L + 10 X 4.2 X 50
Solving for L we have L = 336 J g-1
So specific latent heat of fusion of ice = 336 Jg-1 [ANS]
29) In an experiment to determine the specific Latent heat of vaporisation of steam L, the following measurements were taken:
Mass of calorimeter + stirrer = 𝒙 𝒌𝒈
Mass of water = y kg
Initial temperature of water = T1 °C
Final temperature of mixture = T2 °C
Given: Specific heat capacity of calorimeter and water are S1 and S2 respectively. Express L in terms of above data.
Heat lost by steam to condense = m X L
Heat lost by water to lower its temperature T2 = m X s2 (100-T2)
Heat gained by water = y X S2 (T2 – T1)
Heat gained by calorimeter = 𝑥 X S1 (T2– T1)
Total heat gained = y X S2 (T2 – T1) + 𝑥 X S1 (T2 – T1)
Now, Heat lost by steam = Heat gained by water + Heat gained by calorimeter
Therefore, mL + mS2
(100 – T2) = y X S2 (T2 – T1) + 𝑥 X S1 (T2 – T1)

30) A piece of metal at 10 °C has a mass of 50g. When it is immersed in a current of steam at 100 °c, 0.7 g of steam is condensed on it. Calculate the specific heat of the metal. (Given: Latent heat of steam = 540 Cal/g)
Mass of metal = 50g
Initial temperature = 10 °c
Final temperature = 100 °c
Let ‘c’ be the specific heat in cal/g °C. Then heat gained by metal = 50 g X C X (100-10) °C
= 50 X 90 X C Cal.
Mass of steam condensed = 0.7g
Specific latent heat of steam = 540 cal/g
Heat lost by steam = mL = 0.7 X 540 Cal.
Heat lost by steam = Heat gained by a piece of metal
But, 50 X C X 90 = 0.7 X 540
C = 0.7 X 540 / 50 X 90 = 0.084 𝐶𝑎𝑙 𝑔-1 °C-1
⸫ Specific heat of metal = 0.084 𝐶𝑎𝑙 𝑔-1 °C-1 [ANS]
31) A 30g ice cube at 0 °C is dropped into 200g of water at 30°C. Calculate the final temperature of water when the entire ice cube is melted. Given: Latent heat of ice is 80 cal g-1 Specific heat capacity of water = 1 cal 𝐶𝑎𝑙 𝑔-1 °C-1
Given: mice = 30g
MW = 200g, T1 = 0°C, T2= 30°C, T =?
L ice = 80 cal g-1, S =1 𝐶𝑎𝑙 𝑔-1 °C-1
Heat lost by 200g water in cooling from 30°C to 0°C = 200 X 1 X (30 – T)
= 200 (30-T) cal.
This heat is used by 30g of ice in getting just completely melted and in raising the temperature of
melted water to T°c. Now heat needed to just melt 30g of ice = 30 X 80 = 2400 cal.
Heat needed to raise the temperature of 30g of water from 0°C to T°C = 30 X 1 X (T – 0) cal = 30 T
cal
Thus in equilibrium we have 2400 + 30 T = 200 (30-T) = 6000 -200T
= 200 T + 30 T = 6000-2400
= 230 T = 3600 / 230,
= T = 3600 / 230
= 15.65 °c
⸫ Final temperature of water = 15.65 °c [ANS]
32) 1 Kg of ice at 0 °c is being continuously heated through an electric heater of 1 KW. Assuming that all the heat is transmitted to ice, calculate the time intervals in seconds for water to get heated from 0 °c to 100 °c.
(Given: Specific latent heat of ice = 3,336,000 J Kg-1
Specific heat capacity of water = 4200 J Kg-1 K -1)
Rate of heat energy supplied by the 1 KW electric heater = 1000 J s-1
i. Amount of heat required to completely melt 1 kg of ice at 0 °C
= Specific latent heat of ice
= 336000 J
Hence, time required = 336000 / 1000 = 336 sec [ANS]
ii. Amount of heat required by 1 Kg of water at 0 °c, in getting heated to 100 °c = 1 X 4200 X 100 J = 420000 J.
Hence time needed = 420000 J / 1000
S = 420 sec [ANS]
33) A metal of mass 250g is heated to a temperature of 65 °C. It is then placed in 50g of water at 20 °C.
The final steady temperature of water becomes 25 °C. Neglecting the heat taken by the container; calculate the specific heat capacity of the metal.
Given: m= 250g, T1= 65°C, mW = 50g, T2 = 20 ° C, T = 25 ° C, C= ?
Let ‘c’ be the required specific heat capacity then heat lost by the metal = 250 X C X (65-25) = 10,000CJ
Heat gained by the water = 50 X 4.2 (25-20) 1050J
4 Specific heat capacity of water = 4.2 Jg-1 ° C -1
10000 CJ = 1050 J
⸫ C = 1050 / 10,000 = 0.105 Jg-1 ° C-1
So specific heat capacity of metal is 0.105 J g-1 ° C -1 [ANS]
34) Calculate the heat given out when a piece of iron of mass 50g and specific heat capacity 460 J Kg-1 ° C-1 cools from 100 °c to 40 °c
Mas of the piece of iron m =50g = 0.05 kg
Specific heat capacity of iron, C = 460 J Kg-1 ° C-1
Change in temperature ΔT = (100-40) °C = 60 °C
⸫ Heat energy = m X C X ΔT
= 0.05 X 460 X 60 = 1380 J
Hence, the heat given out by the iron piece is 1380 J [ANS]
35) Calculate the heat energy gained when 5 Kg of water at 20 °C is brought to its boiling point.
(sp. Heat capacity of water = 4200 J Kg-1 ° C-1)
Rise or change in temperature Δ T = 100-20 = 80 °C
⸫ Heat energy gained = mc ΔT
= 5 X 4200 X 80
= 1680000J [ANS]
36) 0.085 Kg of copper of sp. Heat capacity 100 cal kg-1 °C-1 and at 20 °C is heated by a burner for one minutes, which supplies heat energy at a rate of 12 calories/sec. calculate the final temperature of copper.
Let rise in temperature = Δ T
Heat supplied to copper = 12 cal /S 𝑋 60𝑠
= 720 Cal.
Heat supplied = mc ΔT
720 cal = 0.085 Kg X 100 Cal Kg-1 °c-1 X Δ T
⇒ΔT = 720 / 0.085 x 100 °C = 84.70 °C
⸫ Final temperature of copper = 20°C + 84.70°C
= 104.70 ° C [ANS]
37) Calculate the total amount of heat required to convert 100g ice at 0°C to steam at 100°c
(Specific latent heat of fusion of ice = 333 Jg-1)
(Specific heat capacity of water = 4.2 Jg-1 ° C-1)
Heat required to convert 100g ice at 0°C to water at 0°C = Mass X Specific latent heat of fusion of ice
= 100 X 333 = 33300 J
Heat required to raise the temperature of 100g water from 0°C to 100 °C
= Mass X Sp. Heat capacity of water X rise in temperature
= 100 X 4.2 X (100-0) = 42000 J
⸫Total amount of heat required = 33300 + 42000 = 75300J [ANS]
38) 2000 cal of heat is supplied to 200g of water. Find the rise in temperature.
(Take specific heat of water = 1 cal g-1 ° C -1)
Quantity of heat supplied, Q = 2000 cal.
Mass of water, m = 200g
Sp. Heat of water, C = 1 Cal g-1 ° C-1
Rise in temperature = ΔT
We know Q = m X C X ΔT
⇒ Δ T = Q/ mxC = 2000 / 200X = 10° C
39) Calculate the current flowing in a nichrome wire immersed in 500 g of turpentine oil at 20° C. Such that the temperature of the oil rises to 70°C 5 minutes when the wire is connected to a battery of emf 24V. The specific heat capacity of the oil is 750 J Kg-1°c-1
Heat supplied by heating coil = V X I X T
= 24 X I X 5 X 60 J.
Heat gained by turpentine = m X S X t = 500 X 0.75 X 50J
Heat lost = Heat gained
So 24 X I X 5 X 60 = 500 X 0.75 X 50.
⸫ Current flowing = I = 2.60 A [ANS]
40) A refrigerator converts 100g of water at 20°C into ice at -10°C in 1 hr. Calculate the quantity of heat extracted per sound.
Given: Sp. Latent heat of ice = 336 J/g
(Specific heat capacity of ice = 2.1 J/g°C, Sp. Heat capacity of water = 4.2 J/g °C)
Total heat extracted per hour = heat lost by water (being cooled from 20°c to 0°c + freezing to 0°C +
in reducing the temperature of ice to -10°c
= mCw Δ t + mL + mcice + Δt1
=m [Cw Δ t + L + Cice Δ t1]
= 100g [4.2 Jg-1 ° C-1X (20-0) ° C + 336 Jg-1 + 2.1 Jg-1 ° C-1 X {0- (-10) ° C} ]
= 100 [84 + 336 + 21] J
= 44100 J
⸫ Heat extracted per second = 44100 J /3600 S
= 12.25 j/s
= 12.25 W [ANS]
41) 0.5 Kg of ice at -10 °C is heated until whole of it evaporates. Find the amount of heat required.
Given: Latent heat of ice = 336 X 103 J/Kg
Latent heat of steam = 2268 X 103 J/Kg and specific heat capacity of ice = 2.1 X 103+ J/kg °c
Amount of heat required to evaporate 0.5 Kg of ice at -10 °C = Heat required to (raise temperature
of ice from – 10 °C to 0 °C + melt ice + raise the temperature of water from 0 °C to 100 °C + vaporize
the water)
= [m Cice Δ t + mLice + MCW Δ t1 + mL stem]
= m[Cice Δ t + Lice+ CW Δt1 + L steam]
= 0.5[{2.1 X 103 X (0-(-10)} + 336 X 103 + 4.2 X 103 X (100-0) + 2268 X 103]
= 0.5 [21 X 103 + 336 X 103 + 420 X 103 + 2268 X 103] = 1.5225 X 106 J [ANS]
42) A copper vessel contains 200g of water at 24 ° C. When 112g of water at 42°C is added the resultant temperature of water is 30°c. Calculate thermal capacity of calorimeter.
Let thermal capacity of calorimeter is (m XS) J°C-1
Heat gained by the calorimeter = [m X s X (30 – 24)] J
=6 (m X S) J
Heat gained by the water at 24°c
= 200 X4.2 X (30-24) J
= (200 X4.2 X 6) J = 5040 J
Total heat gained by the water + calorimeter = [6 X (m X S) + 5040] J
Heat lost by the water at 42°c = 112 X 4.2 X (42-30) J = 5644.8/J
Heat gained = Heat lost = 6 X (m X S) + 5040 = 5644.8
= 6 X (m X S) = 5644.8 – 5040
= m X S = 604.8 / 6 =100.8 J°C-1
⸫ Thermal capacity of calorimeter = 100.8 J°C-1 [ANS]
43) A vessel of mass 80g (sp. Heat capacity = 0.8 J g -1 ° C-1) contains 250g of water at 35°C. Calculate the amount of ice at 0°c, which must be added to it, so that final temperature is 5°c
[sp. Latent heat of ice = 340 J g -1]
Let amount of ice required is ‘m’ g.
Heat required to change ice at 0°C to water at 0°C = m + 340 = 340m J.
Heat required to change ice at 0°C to water at 5°C water = m X 42 X (5-0) J
= 21 mJ
Total heat gained = (340 m + 21m) = 361 mJ
Heat lost by the water at 35°C to 5° C
= [250 X 4.2 X (35-5)]
= 1050.0 X 30 = 31500 J
Heat lost by the calorimeter = (80 X0.8 X 30 ) J = 1920 J
Total heat lost = (31500 + 1920) J
= 33420 J
According to the question 361 m = 33420
Or, m = 33420 / 361 = 92.57g
∴ The amount of ice = 92.57g [ANS]
44) Calculate the final temperature when 2 kg of cold water at 5°c is mixed with 0.4 Kg of hot water at 95°C.
By the principle of calorimetry heat lost = Heat gained
Let 𝑥 be the final temperature
40.4 X 4200 X (95-𝑥) = 2 X 4200 X (𝑥 − 5)
= 95 − 𝑥 / 𝑥 – = 2/0.4 = 5
= 5
= 95 − 𝑥 = 5𝑥 − 25
= 5𝑥 + 𝑥 = 95 + 25
= 6𝑥 = 120
= 𝑥 =120 / 6
= 20
⸫ Final temperature = 20°C [ANS]
45) A hot solid mass 60gm and at 100°c is placed in 120gm of water at 20°c when final temperature recorded is 22°c. Find the heat capacity of solid.
Heat lost by hot body = Heat gained by cold body
60 X C X (100-22) = 100 X 4.200 X (22-20)
C = 420,000 X 2 /60 X 78 = 14,000 /78 = 0.179 J/g°c
⸫ Heat capacity of solid is 0.179 J/g°C [ANS]
46) 8000 J of heat is given to 200g of copper at 20°c. What is the final temperature if the specific heat
capacity of copper is 0.4 J g -1 °C -1 ?
Let the final temperature of copper be T° C
Then heat required to raise the temperature of 200g of copper from 20°c to T°C
= 200 X 0.4 X (T-20) J
Heat given = 8000J
According to the principle of calorimetry heat gained = Heat lost
Or, 200 X 0.4 X (T-20) = 8000
Or (T-20) = 8000 / 200 X 0.4 = 100
Or, T = 100 + 20 = 120°c
So final temperature of copper is 120°c [ANS]
47) A drill of power 400 W makes a hole in a lead cube of specific heat capacity 0.13 Jg-1 ° C-1 in 80s. If the temperature of lead rises from 25°c to 325°, calculate the mass of lead cube.
Let the mass of lead cube is ‘m’ g .
Heat energy required to heat the lead to raise the temperature from 25° to 325°c = [ m X 0.13 X (325°c-25°c)] J
According to the question
m X 0.13 X (325 – 25) = 400 X 80 or m X 0.13 X 300 =32000 or m = 32000 / 39 or m = 820.5g
So mass of the lead cube is 820.5g [ANS]
48) Which contains more heat 1gm of ice at 0°c or 1 gm of water at 0°c?
1 g of water at 0°c contains more heat. Heat contained by 1gm ice converted from 1gm of water at 0°c = (1 X 336) J = 336 J or heat given out by 1gm of water at 0°c converted from 1gm of ice at 0°c = 336 J
41 gm of water contains more heat than 1gm of ice at 0°c [ANS]
49) A vessel contains 100g of ice and 100g of water at 0°c. Steam at 100°c is passed into this vessel until whole of the ice melts and the temp of the contents is raised by 10°c. Neglecting the heat gained by the vessel, calculate the mass of steam used.
(Sp. Latent heat of fusion of ice is 336J g -1
Sp. Latent heat of vaporisation of steam is 2260 Jg-1
Specific heat capacity of water is 4.2 Jg-1)
Heat lost by steam = mL + mst
= m X 2260 + m X 4.2 X 90
= 2638 mJ
Heat gained by ice = mL + mst
= (100 X 336) + (100 X 4.2 X 10)
= 33600 + 4200.0 = 37800 J
Heat gained by water = mst
= 100 X 4.2 X 10 = 4200 J
Heat lost = heat gained
2638 m = 37800 + 4200 = 42000 or m = 42000/2638 = 15.92g.
⸫ Mass of steam used = 15.92g [ANS]
50) An electric immersion heater is switched on for 10 minutes. The heat supplied by it raises the temperature of 400gm of water from 10°C to 90°C Calculate the power of heater in watts.
Time = 10 min = 600 sec
Let power of heater = P
Energy supplied by heater = P X t = P x 600S
ALSO RISE IN TEMPERATURE OF WATER = ϴR = (90° – 10°) = 80°c
Heat energy absorbed by water = mc ϴR
= 400g X 4.2 Jg-1 ° C-1 X 80°C
= 134400 J
⸫By the law of conservation of energy P X 600s = 134400J
⸫P = 134400 / 60 = 224 J/s = 224 𝑊
Hence the power of heater is 224 watts [ANS]

We hope you liked Heat ICSE Class 10 Physics Notes and solutions. If you have any questions please post them in the comments section below


