Question 1. How much money will be required to buy 400, Rs. 12.50 shares at a premium of Rs. 1?
Solution :
It is given that,
Number of Shares to buy = 400
Nominal value of per share = Rs. 12.50
Premium per share = Rs. 1
Money required to buy a share = Rs. 12.50 + Rs. 1 = Rs. 13.50
Total money required to pay = Number of Shares × Price per share
Total money required to pay = 400 × 13.50
Total money required to pay = Rs. 5,400
Hence, total amount money required to buy 400 shares is Rs. 5,400.
Question 2. How much money will be required to buy 250, Rs. 15 shares at a discount of Rs. 1.50?
Solution :
It is given that,
Number of Shares to buy = 250
Nominal value of per share = Rs. 15
Discount per share = Rs. 1.50
Money require to buy a share = Rs. 13.50
Total money required to pay = Number of Shares × Price per share
Total money required to pay = 250 × Rs. 13.50
Total money required to pay = Rs. 3,375
Hence, total amount money required to buy 250 shares is Rs. 3,375.
Question 3. A person buys 120 shares at a nominal value of Rs. 40 each, which he sells at Rs. 42.50 each. Find his profit and profit percent.
Solution :
It is given that,
Number of Shares to buy = 120
Nominal value of a share = Rs. 40
Selling value of a share = Rs. 42.50
Nominal Value of 120 shares = 120 × Rs. 40
Nominal Value of 120 shares = Rs. 4,800
Market value of 120 shares = Rs. 42.50 × 120
Market value of 120 shares = Rs. 5,100
Amount of Profit = Rs. 5,100 – Rs. 4,800
Amount of Profit = Rs. 300
Profit % = 300/4800 × 100
Profit % = 6.25%
Hence, the profit percentage is 6.25%.
Question 4. Find the cost of 85 shares of Rs. 60 each when quoted at Rs. 63.25.
Solution :
It is given that,
Number of Shares to buy = 85
Market value of a share = Rs. 63.25
Market value of 85 shares = Rs. 63.25 × 85
Market value of 85 shares = Rs. 5,376.25
Hence, the market value of 85 shares is Rs. 5,376.25.
Question 5. A man invests Rs. 800 in buying Rs. 5 shares and when they are selling at a premium of Rs. 1.15, he sells all the shares. Find his profit and profit percent.
Solution :
It is given that,
Amount invested = Rs. 800
Price per share = Rs. 5
Market value of a share = Rs. 5 + Rs. 1.15 = Rs. 6.15
Number of shares purchased = 800/5 = 160
Market value of 160 shares = 160 × 6.15= Rs. 984
Amount of Profit = Rs. 984 – Rs. 800
Amount of Profit = Rs. 184
Profit % = 184/800 × 100
Profit % = 23%
Hence, the profit percentage is 23%
Question 6. Find the annual income derived from 125, Rs. 120 shares paying 5% dividend.
Solution :
It is given that,
Price per share = Rs. 120
Number of shares = 125
Nominal value 250 shares = Rs. 120 × 125
Nominal value 250 shares = Rs. 15,000
Amount of Dividend = Rs. 15,000 × 5%
Amount of Dividend = Rs. 750
Hence, the value of dividend amount Rs. 750.
Question 7. A man invests Rs. 3,072 in a company paying 5% per annum, when its Rs. 10 share can be bought for Rs. 16 each. Find:
(i) his annual income
(ii) his percentage income on his investment.
Solution :
(i) It is given that,
Nominal value of a share = Rs. 10
Market value of a share = Rs. 16
Total Market value of shares = Rs. 3,072
Number of shares = 3072/16
Number of shares = 192
Total Nominal value of shares = 192 × Rs. 10 = Rs. 1920
Average annual payment by the company = Rs. 1920 × 5%
Average annual payment by the company = Rs. 96
Hence, the Average annual payment by the company is Rs. 96
(ii) Average income in percent = 96/3072×100
Average income in percent = 3.125%
Hence, the average income in percent is 3.125%.
Question 8. A man invests Rs. 7,770 in a company paying 5% dividend when a share of nominal value of Rs. 100 sells at a premium of Rs. 5. Find:
(i) the number of shares bought;
(ii) annual income;
(iii) percentage income.
Solution :
It is given that,
Total Investment = Rs. 7,770
Nominal value of a share = Rs. 100
Market value of a share = Rs. 100 + Rs. 5 = Rs. 105
Number of Shares = 7,770/105
Number of Shares = 74
Nominal value of shares = Rs. 100 × 74
Nominal value of shares = Rs. 7,400
Average annual payment by the company = Rs. 7,400 × 5%
Average annual payment by the company = Rs. 370
Average income in percent = 370/7,770×100
Average income in percent = 4.76%
Hence, the average income in percent is 4.76%.
Question 9. A man buys Rs. 50 shares of a company, paying 12% dividend, at a premium of Rs. 10. Find:
(i) the market value of 320 shares;
(ii) his annual income;
(iii) his profit percent.
Solution :
It is given that,
Number of shares = 320 shares
Nominal value of a share = Rs. 50
Premium per share = Rs. 10
Market value of a share = Rs. 50 + Rs. 10 = Rs. 60
Total Market value of shares = 320 × 60 = Rs. 19,200
Total Nominal value of shares = 320 × 5 = Rs. 16,000
Average annual payment by the company = Rs. 16,000 × 12%
Average annual payment by the company = Rs. 1,920
Average income in percent = 1,920/19,200×100
Average income in percent = 10%
Hence, the average income in percent is 10%.
Question 10. A man buys Rs. 75 shares at a discount of Rs. 15 of a company paying 20% dividend. Find:
(i) the market value of 120 shares;
(ii) his annual income;
(ii) his profit percent.
Solution :
It is given that,
Nominal value of a share = Rs. 75
Market value of a share = Rs. 75 – Rs. 15 = Rs. 60
Total Market value of shares = 120 × 60 = Rs. 7,200
Total Nominal value of shares = 120 × 75 = Rs. 9,000
Average annual payment by the company = Rs. 9,000 × 20%
Average annual payment by the company = Rs. 1,800
Average income in percent = 1,800/7,200×100
Average income in percent = 25%
Hence, the average income in percent is 25%.
Question 11. A man has 300, Rs. 50 shares of a company paying 20% dividend. Find his net income after paying 3% income tax.
Solution :
It is given that,
Rate of Dividend = 20%
Nominal value of a share = Rs. 50
Total Nominal value of shares = 300 × 50 = Rs. 15,000
Amount of Dividend = Rs. 15,000 × 20/100
Amount of Dividend = Rs. 3,000
Rate of Income tax = 3%
Amount of Income tax = Rs. 3,000 × 3/100
Amount of Income tax = Rs. 90
Net income = Rs. 3,000 – Rs. 90
Net income = Rs. 2,910
Hence, the net income is Rs. 2910.
Question 12. A company pays a dividend of 15% on its ten-rupee shares from which it deducts income tax at the rate of 22%. Find the annual income of a man who owns one thousand shares of this company.
Solution :
It is given that,
Rate of dividend = 15%
Nominal value of a share = Rs. 10
Total Nominal value of shares = 1000 × 10 = Rs. 10,000
Amount of Dividend = Rs. 10,000 × 15/100
Amount of Dividend = Rs. 1,500
Rate of Income tax = 22%
Amount of Income tax = Rs. 3,000 × 22/100
Amount of Income tax = Rs. 330
Net income = Rs. 1,500 – Rs. 330
Net income = Rs. 1,170
Hence, the net income is Rs. 1,170.
Question 13. A man invests Rs. 8,800 in buying shares of a company of face value of rupees hundred each a premium of 10%. If he earns Rs. 1,200 at the end of the year as dividend, find:
(i) the number of shares he has in the company.
(ii) the dividend percent per share.
Solution :
It is given that,
Total investment = Rs. 8,800
Nominal value of a share = Rs. 100
Market value of a share = Rs. 110
Amount of Dividend = Rs. 1,200
Total Number of shares purchased = 8800/110 = 80
Total Nominal value of shares = 80 × 100 = Rs. 8,000
Let the dividend percent = x%
Amount of Dividend = Nominal Value × Rate of Dividend
Rs. 1,200 = Rs. 8,000 × x%
Rs. 1,200 = Rs. 8,000 × x/100
Rs. 1,200 = 80x
x = 1,200/80
x = 15%
Hence, the dividend rate is 15%.
Question 14. A man invests Rs. 1,680 in buying shares of nominal value Rs. 24 and selling at 12% premium. The dividend on the shares is 15% per annum. Calculate:
(i) the number of shares he buys;
(ii) the dividend he receives annually.
Solution :
It is given that,
Nominal value of a share = Rs. 24
Premium per share = 12%
Dividend Rate per share = 15%
Market value of a share = Nominal value + Premium
Market value of a share = Rs. 24 + 12%
Market value of a share = Rs. 24 + Rs. 2.88
Market value of a share = Rs. 26.88
Total investment = Rs. 1,680
Number of shares purchased = 1680/26.88
Number of shares = 62.5
Nominal value of shares = 62.5 × 24 = Rs. 1,500
Amount of Dividend = 15% of Rs. 1,500
Amount of Dividend = Rs. 1,500 × 15/100
Amount of Dividend = Rs. 225
Hence, the total amount of dividend is 225.
Question 15. By investing Rs. 7,500 in a company paying 10 percent dividend, an annual income of Rs. 500 is received. What price is paid for each of Rs. 100 share?
Solution :
It is given that,
Total investment = Rs. 7,500
Nominal value of share = Rs. 100
Number of shares purchased = x
Rate of the Dividend = 10%
Dividend = Rs. 500
Number of share = 100x/10=Rs.500
Rs. 500 = 100x × 10/100
Rs. 500 = x × 10
Rs. 500 = 10x
x=500/100
Total Market value = 7500/50
Total Market value = Rs.150
Hence, the market value us Rs. 150.
Exercise 3B
Question 1. A man buys 75, Rs. 100 shares of a company which pays 9 percent dividend. He buys shares at such a price that he gets 12 percent of his money. At what price did he buy the shares?
Solution :
It is given that,
Nominal value of a share = Rs. 100
Number of shares = 75
Total Nominal value of shares = 75 × Rs. 100 = Rs. 7,500
Dividend percentage = 9%
Amount of Dividend = Rs. 7,500 × 9%
Amount of Dividend = Rs. 7,500 × 9/100
Amount of Dividend = Rs. 675
Let the market value of a share = x
Total Market value of shares = 75x
It is given that; the profit on investment is 12%.
Profit = Market value × Profit Percent
Rs. 675 = Rs. 75x × 12%

Rs. 5625 = Rs. 75x
Rs. 75x = Rs. 5625
x = Rs. 5625/75
x = Rs. 75
Hence, the market value of share is Rs. 75.
Question 2. By purchasing Rs. 25 gas shares for Rs. 40 each, a man gets 4 percent profit on his investment. What rate percent is the company paying? What is his dividend if he buys 60 shares?
Solution :
It is given that,
Nominal value of a share = Rs. 25
Market value of a share = Rs. 40
Profit percent on investment = 4%
Amount of Profit on a share = 4% of Rs. 40
Amount of Profit on a share = Rs. 1.60
Dividend Percent = 1.6/25 × 100% = 6.4%
Number of shares purchased= 60
Dividend on 60 shares = 60 × Rs. 1.60
Dividend on 60 shares = Rs. 96
Hence, company paying 6.4% dividend and dividend on 60 shares is 96.
Question 3. Hundred rupee shares of a company are available in the market at a premium of Rs. 20. Find the rate of dividend given by the company, when a man’s return on his investment is 15%.
Solution :
It is given that,
Nominal value per share = Rs. 100
Premium per share = Rs. 20
Return on investment = 15%
Market value per share = Rs. 100 + Rs. 20
Market value per share = Rs. 120
Profit per share = 15% of Rs. 120
Profit per share = 120 × 15/100
Profit per share = Rs. 18
Rate of Dividend = 18/100 × 100
Rate of Dividend = 18%
Hence, the rate of dividend is 18%.
Question 4. Rs. 50 shares of a company are quoted at a discount of 10%. Find the rate of dividend given by the company, the return on the investment on these shares being 20 percent.
Solution :
It is given that,
Nominal value per share = Rs. 50
Return on investment = 20%
Rate of Discount = 10%
Amount of Discount = 10% of Rs. 50
Amount of Discount = Rs. 50 × 10/100
Amount of Discount = Rs. 5
Market value per share = Nominal value per share – Amount of Discount
Market value per share = 50 – 5
Market value per share = Rs. 45
We know that, Profit percent on investment = 20%
Profit on share = Rs. 45 × 20%
Profit on share = Rs. 45 × 20/100
Profit on share = Rs. 9
Rate of Dividend = 9/50 × 100
Rate of Dividend = 18%
Hence, the rate of dividend is 18%.
Question 5. A company declares 8 percent dividend to the shareholders. If a man receives Rs. 2,840 as his dividend, find the nominal value of his shares.
Solution :
It is given that,
Rate of Dividend = 8%
Dividend received = Rs. 2,840
It is assumed that,
Nominal value of shares = Rs. x
x×8% = Rs. 2840
x×8/100 = Rs. 2840
x = Rs. 2840 ×100/8
x = Rs. 35000
Hence, the nominal value of the shares is Rs. 35,000.
Question 6. How much should a man invest in Rs. 100 shares selling at Rs. 110 to obtain an annual income of Rs. 1,680, if the dividend declared is 12%?
Solution :
It is given that,
Nominal value per share = Rs. 100
Market value per share = Rs. 110
Let us assumed that,
Number of shares purchased = x
Total Nominal value of shares = Rs. 100 × x
Rate of Dividend = 12%
Amount of Dividend = Rs. 1,680
100x × 12% = Rs. 1,680

Market value of shares = 140 × 110
Market value of shares = Rs. 15,400
Hence, the market value of 140 shares is Rs. 15,400.
Question 7. A company declares a dividend of 11.2% to all its share-holders. If its Rs. 60 share is available in the market at a premium of 25%, how much should Rakesh invest, in buying the shares of this company, in order to have an annual income of Rs. 1,680?
Solution :
It is given that,
Nominal value per share = Rs. 60
Rate of Premium per share = Rs. 25%
Amount of Premium per share = 25% of Rs. 60
Amount of Premium per share = Rs. 60 × 25/100
Amount of Premium per share = Rs. 15
Market value per share = Nominal value + Premium per share
Market value per share = Rs. 60 + Rs. 15
Market value per share = Rs. 75
Let us assumed that,
The number of shares = x
Then nominal value of n shares = Rs. 60x
Rate of Dividend = 11.2%
Amount of Dividend = Rs. 1,680
Let us assumed that,
Number of shares purchased = x
Total Nominal value of shares = Rs. 60 × x
Rate of Dividend = 11.2%
Amount of Dividend = Rs. 1,680
60x × 11.2% = Rs. 1,680

Total Market value of 250 shares = 250 × 75
Total Market value of 250 shares = Rs. 18,750
Hence, the market value of shares is Rs. 18,750.
Question 8. A man buys 400, twenty-rupee shares at a premium of Rs. 4 each and receives a dividend of 12%. Find:
(i) the amount invested by him.
(ii) his total income from the shares.
(ii) percentage return on his money.
Solution :
It is given that,
Number of shares purchased = 400
Nominal value per share = Rs. 20
Premium per share = Rs. 4
Market value per share = Nominal value per share + Premium per share
Market value per share = Rs. 20 + Rs. 4
Market value per share = Rs. 24
(i) Total Investment by the man = 400 × 24
Total Investment by the man = Rs. 9,600
Hence the investment value by the man is Rs. 9,600.
(ii) Rate of dividend = 12%
Amount of dividend = Rs. 8,000 × 12%
Amount of dividend = Rs. 8,000 × 12/100
Amount of dividend = Rs. 960
Hence, the total income from the shares is Rs. 960.
(iii) Return of his money = Rs. 960

Percentage of return = 10%
Hence, the percentage of return is 10%.
Question 9. A man buys 400, twenty-rupee shares at a discount of 20% and receives a return of 12% on his money. Calculate:
(i) the amount invested by him.
(ii) the rate of dividend paid by the company.
Solution :
It is given that,
Number of shares = 400
Nominal value per share = Rs. 20
Return on investment = 12%
Rate of Discount = 20%
Amount of Discount = Rs. 20 × 20%
Amount of Discount = Rs. 4
Market value per share = Nominal value – Discount Amount
Market value per share = Rs. 20 – 4
Market value per share = Rs. 20 – Rs. 4
Market value per share = Rs. 16
(i) Total amount invested by men = 400 × Rs.16
Total amount invested by men = Rs. 6,400
Hence, the total amount invested by men = Rs. 6,400
(ii) Rate of Return% = 12%
Income from shares = Rs. 6,400 × 12%
Income from shares = Rs. 768

Dividend Rate = 9.6%
Hence, the rate of dividend is 9.6%.
Question 10. A company, with 10,000 shares of Rs. 100 each, declares an annual dividend of 5%.
(i) What is the total amount of dividend paid by the company?
(ii) What should be the annual income of a man who has 72 shares in the company?
(iii) If he received only 4% of his investment, find the price he paid for each share.
Solution :
It is given that,
Nominal value per share = Rs. 100
Nominal value of 10,000 shares = 10,000 × Rs. 100
Nominal value of 10,000 shares = Rs. 10,00,000
(i) Rate of Dividend = 5%
Amount of Dividend = Rs. 10,00,000 × 5%
Amount of Dividend = Rs. 10,00,000 × 5/100
Amount of Dividend = Rs. 50,000
Hence, the amount of dividend of 10,000 shares is Rs. 50,000
(ii) Nominal value of 72 shares = Rs. 100 × 72
Nominal value of 72 shares = Rs. 7,200
Amount of Dividend = Rs. 7,200 × 5%
Amount of Dividend = Rs. 7,200 × 5/100
Amount of Dividend = Rs. 360
Hence, the amount of dividend of 72 shares is Rs. 360
(iii) Let us assumed that,
Market value per share = Rs. x
Market value of 10,000 shares = 10,000 × Rs. x
Market value of 10,000 shares = Rs. 10,000x
Rate of Return = 4%
Amount of Dividend = Rs. 50,000
Rs. 10,000x × 4% = Rs. 50,000

Hence, the Market value of the share is Rs. 125.
Question 11. A lady holds 1800, Rs. 100 shares of a company that pays 15% dividend annually. Calculate her annual dividend. If she had bought these shares at 40% premium, what is the return she gets as percent on her investment? Give your answer to the nearest integer.
Solution :
It is given that,
Nominal value per share = Rs. 100
Rate of Dividend = 15%
Premium per share = 40%
Market value per share = Rs. 100 + Rs. 100 × 40%
Market value per share = Rs. 100 + Rs. 40
Market value per share = Rs. 140
No. of shares purchased = 1800
Nominal value of 1800 shares = 1800 × 100 = Rs. 1,80,000
Market value of 1800 shares= 1800 × 140 = Rs. 2,52,000
Amount of Dividend = Rs. 1,80,000 × 15%
Amount of Dividend = Rs. 1,80,000 × 15/100
Amount of Dividend = Rs. 27,000

Hence, the rate of return is 11%.
Question 12. A man invests Rs. 11,200 in a company paying 6 percent per annum when its Rs. 100 shares can be bought for Rs. 140. Find:
(i) his annual dividend
(ii) his percentage return on his investment.
Solution :
It is given that,
Nominal value of per share = Rs. 100
Market value of per share = Rs. 140
Rate of dividend = 6%
Amount Invested = Rs. 11,200
Number of shares = 11,200/140
Number of shares = 80 shares
Nominal value of 80 shares = 80 × 100
Nominal value of 80 shares = Rs. 8,000
(i) Rate of Dividend = 6%
Amount of Dividend = Rs. 8,000 × 6%
Amount of Dividend = Rs. 8,000 × 6/100
Amount of Dividend = Rs. 480
Hence, the amount of dividend is Rs. 480.

Hence, the rate of return is 4.29%
Question 13. Mr. Sharma has 60 shares of nominal value Rs. 100 and decides to sell them when they are at a premium of 60%.
He invests the proceeds in shares of nominal value Rs. 50, quoted at 4% discount, and paying 18% dividend annually. Calculate:
(i) the sale proceeds
(ii) the number of shares he buys and
(iii) his annual dividend from the shares.
Solution :
(i) It is given that,
Nominal value per share = Rs. 100
Nominal value of 60 shares = Rs. 100 × 60
Nominal value of 60 shares = Rs. 6,000
Market value per share = Rs. 100 + Rs. 100 × 60%
Market value per share = Rs. 100 + Rs. 60
Market value per share = Rs. 160
Market value of 60 shares = Rs. 160 × 60
Market value of 60 shares = Rs. 9,600
Hence, the market value of 60 shares is Rs. 9,600.
(ii) Nominal value per share = Rs. 50
Discount Rate = 4%
Market value per share = Nominal value – Discount
Market value per share = Rs. 50 – Rs. 50 × 4%
Market value per share = Rs. 50 – Rs. 2
Market value per share = Rs. 48
Number of shares = 9600/48
Number of shares = 200
Hence, the number of shares is 200.
(iii) Nominal value per share = Rs. 50
Dividend Rate = 18%
Nominal value of 200 shares = Rs. 50 × 200
Nominal value of 200 shares = Rs. 10,000
Amount of Dividend = Rs. 10,000 × 18%
Amount of Dividend = Rs. 10,000 × 18/100
Amount of Dividend = Rs. 1,800
Hence, the amount of dividend is Rs. 1,800.
Question 14. A company with 10,000 shares of nominal value Rs. 100 declares an annual dividend of 8% to the share-holders.
(i) Calculate the total amount of dividend paid by the company.
(ii) Ramesh had bought 90 shares of the company at Rs. 150 per share. Calculate the dividend he receives and the percentage of return on his investment.
Solution :
(i) It is given that,
Nominal value per share = Rs. 100
Dividend Rate = 8%
Nominal value of 10,000 shares = Rs. 100 × 10,000
Nominal value of 10,000 shares = Rs. 10,00,000
Amount of Dividend = Rs. 10,00,000 × 8%
Amount of Dividend = Rs. 10,00,000 × 8/100
Amount of Dividend = Rs. 80,000
Hence, the amount of dividend is Rs. 80,000
(ii) Market value of 90 shares = Rs. 150 × 90
Market value of 90 shares = Rs. 13,500
Nominal value of 90 shares = Rs. 100 × 90
Nominal value of 90 shares = Rs. 9,000
Amount of Dividend = Rs. 9,000 × 8%
Amount of Dividend = Rs. 9,000 × 8/100
Amount of Dividend = Rs. 720
Hence, the amount of dividend is Rs. 720

Hence, the rate of return is 5.33%
Question 15. Which is the better investment:
16% Rs. 100 shares at 80 or 20% Rs. 100 shares at 120?
Solution :
(i) 16% of Rs. 100 shares at 80
It is given that,
Nominal value per share = Rs. 100
Market value per share = Rs. 80
Rate of Dividend = 16%
Income on Market value (Rs. 80) = Rs. 100 × 16%
Income on Market value (Rs. 80) = Rs. 16
Income per share = 16/80 = Rs. 0.20
(ii) 20% of Rs. 100 shares at 120
It is given that,
Nominal value per share = Rs. 100
Market value per share = Rs. 120
Rate of Dividend = 20%
Income on Market value (Rs. 120) = Rs. 100 × 20%
Income on Market value (Rs. 120) = Rs. 20
Income per share = 20/120 = Rs. 0.17
Hence, 16% Rs. 100 shares at 80 is better investment.
Question 16. A man has a choice to invest in hundred-rupee shares of two firms at Rs. 120 or at Rs. 132. The first firm pays a dividend of 5% per annum and the second firm pays a dividend of 6% per annum. Find:
(i) which company is giving a better return.
(ii) if a man invests Rs. 26,400 with each firm, how much will be the difference between the annual returns from the two firms.
Solution :
(i) It is given that,
Market value per share = Rs. 120
Nominal value per share = Rs. 100
Rate of Dividend = 5%
Income on Market value (Rs. 120) = Rs. 100 × 5%
Income on Market value (Rs. 120) = Rs. 5
Income per share = 5/120 = Rs. 0.041
(ii) It is given that,
Market value per share = Rs. 132
Nominal value per share = Rs. 100
Rate of Dividend = 6%
Income on Market value (Rs. 132) = Rs. 100 × 6%
Income on Market value (Rs. 132) = Rs. 6
Income per share = 6/132 = Rs. 0.045
Hence, company second is giving the better return.
(ii) Amount invested by the men first company = Rs. 26,400
Income on investment from first firm = 5/120 × 26,400
Income on investment from first firm = Rs. 1,100
Amount invested by the men in second company = Rs. 26,400
Income on investment from first firm = 6/132 × 26,400
Income on investment from first firm = Rs. 1,200
Difference between the annual returns from the two firms = Rs. 1,200 – Rs. 1,100 = Rs. 100
Hence, the difference between the annual return from the two firms is Rs.100.
Question 17. A man bought 360, ten-rupee shares of a company, paying 12% per annum. He sold the shares when their price rose to Rs. 21 per share and invested the proceeds in five-rupee shares paying 4.5 percent per annum at Rs. 3.50 per share. Find the annual change in his income.
Solution :
(i) It is given that,
Nominal value per share = Rs. 10
Nominal value of 360 shares = Rs. 10 × 360 = Rs. 3,600
Market value per share = Rs. 21
Market value of 360 shares = Rs. 21 × 360 = Rs. 7,560
Rate of Dividend = 12%
Amount of Dividend = Rs. 3,600 × 12%
Amount of Dividend = 3,600 × 12/100
Amount of Dividend = Rs. 432
(ii) It is given that,
Nominal value per share= Rs. 5
Market value per share= Rs. 3.50
Number of shares = 7560/3.50
Number of shares = 2,160 shares
Nominal value of 2160 shares = Rs. 5 × 2160
Nominal value of 2160 shares = Rs. 10,800
Dividend Rate = 4.5%
Amount of Dividend = Rs. 10,800 × 4.5%
Amount of Dividend = Rs. 486
Difference between the annual returns = Rs. 486 – Rs. 432
Difference between the annual returns = Rs. 54
Hence, the annual change in his income is Rs. 54.
Question 18. A man sold 400 (Rs. 20) shares of a company, paying 5% at Rs. 18 and invested the proceeds in (Rs. 10) shares of another company paying 7% at Rs. 12. How many (Rs. 10) shares did he buy and what was the change in his income?
Solution :
(i) It is given that,
Nominal value per share = Rs. 20
Market value per share = Rs. 18
Nominal value of 400 shares = Rs. 20 x 400
Nominal value of 400 shares = Rs. 8,000
Market value of 400 shares = Rs. 18 x 400
Market value of 400 shares = Rs. 7,200
Dividend Rate = 5%
Amount of Dividend = Rs. 8,000 × 5%
Amount of Dividend = Rs. 8,000 × 5/10
Amount of Dividend = Rs. 400
(ii) It is given that,
Nominal value per share = Rs. 10
Market value per share = Rs. 12
Number of shares = 7200/12
Number of shares = 600
Nominal value of 600 shares = Rs. 10 × 600
Nominal value of 600 shares = Rs. 6,000
Dividend Rate = 7%
Amount of Dividend = Rs. 6,000 × 7%
Amount of Dividend = 6,000 × 7/100
Amount of Dividend = Rs. 420
Change in his income = Rs. 420 – Rs. 400
Change in his income = Rs. 20
Hence, the change in his income is Rs. 20.
Question 19. Two brothers A and B invest Rs. 16,000 each in buying shares of two companies. A buys 3% hundred-rupee shares at 80 and B buys ten-rupee shares at par. If they both receive equal dividend at the end of the year, find the rate per cent of the dividend received by B.
Solution :
(i) It is given that,
Total amount invested by A = Rs. 16,000
Nominal value of 1 share = Rs. 100
Market value of 1 share = Rs. 80
Number of shares = 16000/80
Number of shares = 200
Nominal value of 200 shares = Rs. 100 × 200
Nominal value of 200 shares = Rs. 20,000
Dividend Rate = 3%
Dividend Amount = Rs. 20,000 × 3%
Dividend Amount = Rs. 20,000 × 3/100
Dividend Amount = Rs. 600
(ii) It is given that,
Total amount invested by B = Rs. 16,000
Nominal value per share = Rs. 10
Market value per share= Rs. 10
Number of shares = 16000/10
Number of shares = 1600
Nominal value of 1600 shares = 10 × 1600
Nominal value of 1600 shares = Rs. 16,000
It is given that,
Dividend received by B is equal to A.
Dividend received by B = Dividend received by A = Rs. 600

Hence, the rate of dividend 3.75%.
Question 20. A man invests Rs. 20,020 in buying shares of nominal value Rs. 26 at 10% premium. The dividend on the shares is 15% per annum. Calculate:
(i) the number of shares he buys.
(ii) the dividend he receives annually.
(iii) the rate of interest he gets on his money.
Solution :
It is given that,
Total amount invested = Rs. 20,020
Nominal value per share = Rs. 26
Premium per share = 10%
Market value per share = Nominal value + Amount of Premium
Market value per share = Rs. 26 + Rs. 26 × 10%
Market value per share = Rs. 26+ Rs. 2.60
Market value per share = Rs. 28.60
Number of shares purchased = 20,020/28.60 = 700
Nominal value of 700 shares = Rs. 26 × 700
Nominal value of 700 shares = Rs. 18,200
Rate of Dividend = 15%
Amount of Dividend = Rs. 18,200 × 15%
Amount of Dividend = Rs. 18,200 × 15/100
Amount of Dividend = Rs. 2,730

Hence, the rate of return is 13.63%
Exercise 3C
Question 1. By investing Rs. 45,000 in 10% Rs. 100 shares, Sharad gets Rs. 3,000 as dividend. Find the market value of each share.
Solution :
It is given that,
Total amount invested = Rs. 45,000
Nominal Value of a share = Rs. 100
Rate of Return = 10%
Annual income from a share = Rs. 100 × 10%
Annual income from a share = Rs. 100 × 10/100
Annual income from a share = Rs. 10
Total Annual income = Rs. 3,000

Market value of a share = Rs. 150
Hence, the market value of a share is Rs. 150.
Question 2. Mrs. Kulkarni invests Rs. 1,31,040 in buying Rs. 100 shares at a discount of 9%. She sells shares worth Rs. 72,000 at a premium of 10% and the rest at a discount of 5%. Find her total gain or loss on the whole.
Solution :
It is given that,
Total amount invested = Rs. 1,31,040
Nominal value per share = Rs. 100
Discount Rate = 9%
Discount Amount = Rs. 100 × 9%
Discount Amount = Rs. 9
Market value per share = Nominal Value – Discount Amount
Market value per share = Rs. 100 – Rs. 9
Market value per share = Rs. 91

720 shares sold by Mrs. Kulkarni at a premium of 10%
Market Value per share = Nominal Value + Premium Amount
Market Value per share = Rs. 100 + Rs. 10
Market Value per share = Rs. 110
Market value of shares = Number of shares × Market value per share
Market value of 720 shares = 720 × Rs. 110
Market value of 720 shares = Rs. 79,200
Remaining shares = 1440 – 720 = 720
She sells 720 shares at a discount of 5%
Market Value per share = Nominal Value – Discount
Market Value per share = Rs. 100 – Rs. 5
Market Value per share = Rs. 95
Market Value of 720 shares = Rs. 720 × Rs. 95
Market Value of 720 shares = Rs. 68,400
Total selling price = Rs. 79200 + Rs. 68400
Total selling price = Rs. 147600
Gain = Total selling price – Total investment
Gain = Rs. 1,47,600 – Rs. 1,31,040
Gain = Rs. 16,560
Hence, the total gain is Rs. 16,560.
Question 3. A man invests a certain sum on buying 15% Rs. 100 shares at 20% premium. Find:
(i) His income from one share
(ii) The number of shares bought to have an income, from the dividend, Rs. 6480
(iii) Sum invested
Solution :
(i) Rate of Dividend = 15%
Dividend per share = Rs. 100 × 15%
Dividend per share = Rs. 100 × 15/100
Dividend per share = Rs. 15
Hence, the income per share is Rs. 15.
(ii) Number of shares = (Total Income)/(Annual Income per share)
Number of shares = 6480/15
Number of shares = 432
Hence, the number of shares is 432.
(iii) Premium per share = 20%
Nominal value = 100
Market value per share = Nominal value + Premium
Market value per share = Rs. 100 + Rs. 100 × 20%
Market value per share = Rs. 100 + Rs. 20
Market value per share = Rs. 120
Amount Invested = Number of shares × Market value per share
Amount Invested = 432 × 120
Amount Invested = 51,840
Question 4. Gagan invested Rs. 80% of his savings in 10% Rs. 100 shares at 20% premium and the rest of his savings in 20% Rs. 50 shares at Rs. 20% discount. If his incomes from these shares is Rs. 5,600 calculate:
(i) His investment in shares on the whole
(ii) The number of shares of first kind that he bought
(iii) Percentage return, on the shares bought on the whole.
Solution :
(i) For 1st part
Let us assumed that,
Total savings = Rs. x
Nominal value per share = Rs. 100
Rate of dividend = 10%
Amount of investment = Rs. x × 80%
Amount of investment = Rs. 0.80x
Market value per share = Nominal value + Premium
Market value per share = Rs. 100 + Rs. 100 × 20%
Market value per share = Rs. 100 + Rs. 20
Market value per share = Rs. 120
Number of share = (Amount of investment)/(Market value)
Number of share = 0.8x/120
Amount of Dividend = 100 × 10%
Amount of Dividend = Rs. 10
Total Amount Dividend = 10 × 0.8x/120
Total Amount Dividend = 0.8x/12
Hence, the total amount of dividend is 0.8x/12.
For 2nd part
Nominal value per share = Rs. 50
Rate of dividend = 10%
Amount of investment = Rs. x × 20%
Amount of investment = Rs. 0.20x
Market value per share = Nominal value + Discount
Market value per share = Rs. 50 – Rs. 50 × 20%
Market value per share = Rs. 50 – Rs. 10
Market value per share = Rs. 40
Number of share = (Amount of investment)/(Market value)
Number of share = 0.20x/40
Amount of Dividend = Rs. 50 × 20%
Amount of Dividend = Rs. 10
Total Amount Dividend = 10 × 0.2x/40
Total Amount Dividend = 0.2x/4
Total dividend from both the investments is Rs. 5,600.

Hence, the investment in share on the whole is Rs. 48,000.

Question 5. Ashwarya bought 496, Rs. 100 shares at Rs. 132 each, find:
(i) Investment made by her
(ii) Income of Ashwarya from these shares, if the rate of dividend is 7.5%.
(iii) How much extra must ashwarya invest in order to increase her income by Rs. 7,200.
Solution :
(i) It is given that,
Nominal Value per share = Rs. 100
Market Value per share = Rs. 132
Total Investment made by Ashwarya = 496 × Rs. 132
Total Investment made by Ashwarya = Rs. 65,472
(ii) It is given that,
Dividend per share = 7.5%
Amount of dividend = Rs. 100 × 7.5%
Amount of dividend = Rs. 7.5
Ashwarya’s Income from these shares = 496 × Rs. 7.5
Ashwarya’s Income from these shares = Rs. 3,720
(iii) Ashwarya wants to increase her income by Rs. 7,200.
Number of shares share buy = (Increase in the income)/(Income per share)
Number of shares share buy = (7,200)/(7.5)
Number of shares share buy = 960
Amount of investment = 960 × 7.5
Amount of investment = Rs. 1,26,720
Hence, Ashwarya should invest Rs. 1,26,720.
A company pays a dividend of 15% on its Rs. 100 shares from which income tax at the rate of 20% is deducted. Find:
(i) The net annual income of Gopal who owns 7,200 shares of this company.
(ii) The sum invested by Ramesh when the shares of this company are bought by him at 20% premium and the gain required by him (after deduction of income tax) is Rs. 9,000.
Solution :
(i) Let us assumed that, Number of shares = x
Nominal value per share = Rs. 100
Rate of dividend = 15%
Total money invested = 100 × x
Total money invested = 100x
Calculation of Annual income:-
Annual income = Total money invested × Rate of dividend
Annual income = 100x × 15/100
Annual income = 15x
Rate of income tax 20%
Net income earned by Gopal = Annual income – Tax
Net income earned by Gopal = 15x – 15x × 20%
Net income earned by Gopal = 15x – 3x
Net income earned by Gopal = 12x
The net annual income of Gopal from 7,200 shares:-
Net annual income of Gopal from 7,200 shares = 12 × Rs. 7200
Net annual income of Gopal from 7,200 shares = Rs. 86,400
Hence, the annual income of Gopal from 7,200 shares Rs. 86,400.
(ii) Let the amount invested by him Rs. y
Nominal value per share = Rs. 100
Rate of Premium = 20%
Amount of Premium = 100 × 20%
Amount of Premium = Rs. 20
Market value per share = Nominal Value + Premium
Market value per share = Rs. 100 + Rs. 20
Market value per share = Rs. 120
Number of shares = y/120
Rate of dividend = 15%
Amount of dividend = Rs. 100 × 15%
Rate of dividend = Rs. 15
Total amount of dividend = Rs. 15 × y/120
Total amount of dividend = Rs. y/8
Rate of income tax = 20%
Total Gain = Total Income – Income tax

Mr. Joseph sold some Rs. 100 shares paying 10% dividend at a discount of 25% and invested the proceeds in Rs. 100 shares paying 16% dividend at a discount of 20%. By doing so, his income was increased by Rs. 4,800. Find the number of shares originally held by Mr. Joseph.
Solution :
Let us assumed that, Number of shares = x
Nominal value per share = Rs. 100
Rate of dividend = 10%
Total money invested = 100 × x
Total money invested = 100x
Calculation of Annual income:-
Annual income = Total money invested × Rate of dividend
Annual income = 100x × 10/100
Annual income = 10x
Rate of discount = 25%
Market value of share = Nominal value – Discount
Market value of share = Rs. 100 – Rs. 100 × 25%
Market value of share = Rs. 100 – Rs. 25
Market value of share = Rs. 75
Market value of x shares = 75x
Now,
Amount invested = 75x
Nominal value per share = Rs. 100
Rate of discount = 20%
Market value per share = Nominal value – Discount
Market value per share = Rs. 100 – Rs. 100 × 20%
Market value per share = Rs. 100 – Rs. 20
Market value per share = Rs. 80
Rate of dividend = 16%
Number of shares = 75x/80
Rate of dividend = 16%
Amount of dividend = Rs. 100 × 16%
Rate of dividend = Rs. 16
Total amount of dividend = Rs. 16 × 75x/80
Total amount of dividend = Rs. 15x
15x – 10 x = 4,800
5x = 4,800
x = 4,800/5
x = 960
Hence, the original numbers of shares are 960.
Question 6. Gopal has some Rs. 100 shares of company A, paying 10% dividend. He sells a certain number of these shares at a discount of 20% and invests the proceeds in Rs. 100 shares at Rs. 60 of company B paying 20% dividend. If his income, from the shares sold, increases by Rs. 18,000, find the number of shares sold by Gopal.
Solution :
It is given that,
Nominal value of share = Rs. 100
Rate of Dividend = 10%
Let us assumed that, the number of shares are sold be x.
Amount of dividend = Rs. 100 × 10%
Amount of dividend = Rs. 10
Total amount of dividend of x shares = Amount of dividend × dividend per share
Total amount of dividend of x shares = x × 10
Total amount of dividend of x shares = 10x
Market value per share = Nominal value – Discount
Market value per share = Rs. 100 – Rs. 100 × 20%
Market value per share = Rs. 100 – Rs. 20
Market value per share = Rs. 80
Total market value of x shares = x × 80
Total amount of dividend of x shares = 80x
Now,
Nominal value per share = Rs. 100
Market value per share = Rs. 60
Number of shares = (Total Amount invested )/(Market value per share)
Number of shares = (80x )/60
Number of shares = (4x )/3
Dividend per share = 100 × 20%
Dividend per share = Rs. 20
Total Dividend received = Number of shares × Dividend per share
Total Dividend received = 4x/3 × 20
Total Dividend received = 80x/3
It is given that, increase in the income = Rs. 18,000

Hence, the number of share sold by Gopal is 1080.
Question 7. A man invests a certain sum of money in 6% hundred-rupee shares at Rs. 12 premium. When the shares fell to Rs. 96, he sold out all the shares bought and invested the proceed in 10%, ten-rupee shares at Rs. 8. If the change in his income is Rs. 540, Find the sum invested originally.
Solution :
It is given that,
Nominal value per share = Rs. 100
Rate of Premium = 12%
Market value per share = Nominal value + Premium
Market value per share = Rs. 100 + Rs. 100 × 12%
Market value per share = Rs. 112
Let the original amount invested be x.
Number of shares = x/112
Income per share = 100 × 6%
Income per share = Rs. 6
Total Income = Number of shares × Income per share
Total Income = x/112 × Rs. 6
Total Income = 3x/56
Now, Sale of share at Rs. 96 per share

Income per share = Rs. 100 × 10%
Income per share = Rs. 1
Total Income = Number of shares × Income per share

Hence, original sum invested is Rs. 10,080.
Question 8. Mr. Gupta has a choice to invest in ten-rupee shares of two firms at Rs. 13 or at Rs. 16. If the first firm pays 5% dividend and the second firm pays 6% dividend per annum, find:
(i) which firm is paying better.
(ii) if Mr. Gupta invests equally in both the firms and the difference between the returns from them is Rs. 30, find how much, in all, does he invest.
Solution :
(i) It is given that, about first firm
Nominal value per share = Rs. 10
Market value per share = Rs. 13
Rate of Dividend = 5%
Amount of Dividend = Rs. 10 × 5%
Amount of Dividend = Rs. 0.50

(ii) It is given that, about second firm
Nominal value per share = Rs. 10
Market value per share = Rs. 16
Rate of Dividend = 6%
Amount of Dividend = Rs. 10 × 6%
Amount of Dividend = Rs. 0.60


x=30×1040
x=Rs.31,200
Amount invested by both = Rs. 31,200 × 2 = Rs. 62,400
Hence, the total amount invested by both firm Rs. 62,400.
Question 9. Ashok invested Rs. 26,400 in 12%, Rs. 25 shares of a company. If he receives a dividend of Rs. 2,475, find the:
(i) number of shares he bought.
(ii) market value of each share.
Solution :
(i) It is given that,
Total dividend received = Rs. 2,475
Rate of dividend = 12%
Nominal value per share = Rs. 25
Dividend per share = Nominal value × Rate of dividend
Dividend per share = 25 × 12%
Dividend per share = Rs. 3

Hence, the numbers of shares are 825.
(ii) Total Amount invested = Rs. 26,400
Number of shares = 825
Market value of each share = 26,400/825
Market value of each share = Rs. 32
Hence, the market value of each shares Rs. 32
Question 10. A man invested Rs. 45,000 in 15% Rs. 100 shares quoted at Rs. 125. When the market value of these shares rose to Rs. 140, he sold some shares, just enough to raise Rs. 8,400. Calculate:
(i) the number of shares he still holds;
(ii) the dividend due to him on these remaining shares.
Solution :
(i) It is given that,
Total amount investment = Rs. 45,000
Market value per share = Rs. 125
Number of shares purchased = 45,000/125
Number of shares purchased = 360
Nominal value of shares = Rs. 100 × 360
Nominal value of shares = Rs. 36,000
Now,
Let us assumed that, the number of share sold = x
Market value per share = Rs. 140
Market value of all shares = Rs. 8,400
x = 8,400/140
x = 60
Remaining shares = 360 – 60 = 300
Hence, 300 shares are still hold with him.
(ii) Number of remaining shares = 300
Nominal value of remaining shares = Rs. 100 × 300
Nominal value of remaining shares = Rs. 30,000
Rate of Dividend = 15%
Amount of Dividend = Rs. 30,000 × 15%
Amount of Dividend = Rs. 30,000 × 15/100
Amount of Dividend = Rs. 4,500
Hence, the amount of dividend on remaining shares is Rs. 4,500
Question 11. Mr.Tiwari. invested Rs. 29,040 in 15% Rs100 shares quoted at a premium of 20%. Calculate:
(i) the number of shares bought by Mr. Tiwari.
(ii) Mr. Tiwari’s income from the investment.
(iii) the percentage return on his investment.
Solution :
It is given that,
Total amount invested = Rs. 29,040
Nominal value per share = Rs. 100
Rate of premium = 20%
Market value per share = Nominal value + Rate of premium
Market value per share = Rs. 100 + Rs. 100 × 20%
Market value per share = Rs. 100 + Rs. 20
Market value per share = Rs. 120

Number of Shares = 242
Total Nominal value of shares = Rs. 100 × 242
Total Nominal value of shares = Rs. 24,200
Rate of Dividend = 15%
Amount of Dividend = Rs. 24,200 × 15%
Amount of Dividend = Rs. 3630

Question 12. A dividend of 12% was declared on Rs. 150 shares selling at a certain price. If the rate of return is 10%, calculate:
(i) the market value of the shares.
(ii) the amount to be invested to obtain an annual dividend of Rs. 1,350.
Solution :
(i) It is given that,
Nominal value per share = Rs. 150
Rate of dividend = 12%
Amount of dividend per share = Rs. 150 × 12%
Amount of dividend per share = Rs. 18
Let us assumed that,
Market value per share = Rs. x
Rate of Return = 10%
Rs. x × 10% = Rs. 18
Rs. x × 10/100 = Rs. 18
Rs. x = Rs. 180
(ii) Total amount invested = 180/18×1350
Total amount invested = 13,500
Hence, the total amount invested is Rs. 13,500.
Question 13. Divide Rs. 50,760 into two parts such that if one part is invested in 8% Rs. 100 shares at 8% discount and the other in 9% Rs. 100 shares at 8% premium, the annual incomes from both the investments are equal.
Solution :
It is given that,
Total amount invested = Rs. 50,760
Let the first part money to be invested = x
Total amount invested in second part = (Rs. 50,760 – x)
Nominal value per share = Rs. 100
Discount per share = 8%
Market value per share = Nominal value – Discount
Market value per share = Rs. 100 – Rs. 100 × 8%
Market value per share = Rs. 100 – Rs. 8
Market value per share = Rs. 92

Rate of dividend = 8%
Amount of dividend = Rs. 100 × 8%
Amount of dividend = Rs. 8
Total amount of dividend = x/92 × 8
Total amount of dividend = 2x/23
Nominal value per share = Rs. 100
Premium per share = 8%
Market value per share = Nominal value – Premium
Market value per share = Rs. 100 + Rs. 100 × 8%
Market value per share = Rs. 100 + Rs. 8
Market value per share = Rs. 108

2x×108=23(456840-9y)
216x=23×456840-207y
216x+207y=23×456840
423x=23×456840
x=(23×456840)/423
x=24,840
Investment in Part first = Rs. 24,840
Investment in Part second = Rs. 50,760 – Rs. 24,840 = Rs. 25,920
Hence, the amount invested in part first and part second be 24,840 and 25,920 respectively.
Question 14. Mr. Shameem invested 33 1/3% of his savings in 20% Rs. 50 shares quoted at Rs. 60 and the remainder of the savings in 10% Rs. 100 share quoted at Rs. 110. If his total income from these investments is Rs. 9,200; find:
(i) his total savings
(ii) the number of Rs. 50 share
(iii) the number of Rs. 100 share.
Solution :
Case 1:-
Let us assumed that the total savings of Mr. Shameem is Rs. x
Total investment = Rs. x × 33 1/3%
Total investment = Rs. x × 100/(3×100)
Total investment = Rs. x × 1/3
Total investment = Rs. x/3
It is given that,
Nominal value per share = Rs. 50
Market value per share = Rs. 60

Case 2:-


Question 15. Vivek invests Rs. 4,500 in 8%, Rs. 10 shares at Rs. 5. He sells the shares when the price rises to Rs. 30, and invests the proceeds in 12% Rs. 100 shares at Rs. 125. Calculate:
(i) the sale proceeds
(ii) the number of Rs. 125 shares he buys.
(iii) the change in his annual income from dividend.
Solution :
Case 1:-
Total amount invested = Rs. 4,500
Market value per share = Rs. 15
Number of shares = 4500/15
Number of shares = 300
Nominal value per share = Rs. 10
Total Nominal value of shares = Rs. 10 × 300
Total Nominal value of shares = Rs. 3,000
Rate of Dividend = 8%
Rate of Dividend = Rs. 3,000 × 8%
Amount Dividend = 8/100 × 3,000
Amount Dividend = Rs. 240
Sale price per share = Rs. 30
Total sale price= Rs. 30 × 300
Total sale price = Rs. 9,000
(ii) Market price per share = Rs. 125
Number of shares = 9000/125
Number of shares = 72 shares
(iii) Nominal value per share = Rs. 100
New nominal value of 72 shares = Rs. 100 × 72 = Rs. 7,200
Rate of Dividend = 12%
Amount of Dividend = Rs. 7,200 × 12%
Amount of Dividend = 12/100 × 7,200
Amount of Dividend = Rs. 864
The change in his annual income from dividend = Rs. 864 – Rs. 240
The change in his annual income from dividend = Rs. 624
Hence, the change in his annual income from dividend Rs. 624.
Question 16. Mr.Parekh invested Rs. 52,000 on Rs. 100 shares at a discount of Rs. 20 paying 8% dividend. At the end of one year he sells the shares at a premium of Rs. 20. Find:
(i) The annual dividend
(ii) The profit earned including his dividend.
Solution :
It is given that,
Rate of dividend = 8%
Total Amount Investment = Rs. 52,000
Market Rate = Rs. 100 – 20 = Rs. 80
Number of shares = 52,000/80
Number of shares = 650
(i) Annual dividend = 650 × 8
Annual dividend = Rs. 5,200
Hence, the annual dividend is Rs. 5,200.
(ii) Market value per share = Rs. 100 + 20
Market value per share = Rs. 120
Total Market value of shares = 650 × 120
Total Market value of shares = Rs. 78,000
Total Profit = Rs. 78,000 – Rs. 52,000
Total Profit = Rs. 26,000
Total Gain = Profit + Dividend
Total gain = Rs. 26,000 + Rs. 5,200
Total gain = Rs. 31,200
Hence, total gain is Rs. 31,200.
Question 17. Salman buys 50 shares of face value Rs. 100 available at Rs. 132.
(i) What is his investment?
(ii) If the dividend is 7.5%, what will be his annual income?
(iii) If he wants to increase his annual income by Rs. 150, how many extra shares should he buy?
Solution :
It is given that,
Total number of share = 50
Nominal value of share = Rs. 100
Market value of share = Rs. 132
(i) Total investment = Number of shares × Market value of shares
Total investment = 50 × Rs. 132
Total investment = Rs. 6,600
(ii) Rate of dividend = 7.5%
Amount of dividend = 100 × 7.5%
Amount of dividend = Rs. 7.50
Annual income = Number of shares × Dividend per share
Annual income = 50 × Rs. 7.50
Annual income = Rs. 375
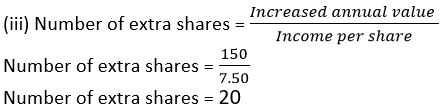
Question 18. Salman invests a sum of money in Rs. 50 shares, paying 15% dividend quoted at 20% premium. If his annual dividend is Rs. 600, calculate:
(i) The number of shares he bought.
(ii) His total investment.
(iii) The rate of return on his investment.
Solution :
It is given that,
Nominal Value per share = Rs. 50
Premium = 20%
Market Value per share = Nominal value + Premium
Market Value per share = Rs. 50 + (50×20%)
Market Value per share = Rs. 50 + Rs. 10
Market Value per share = Rs. 60
Rate of dividend = 15%
Amount of dividend = Rs. 50 × 15%
Amount of dividend = Rs. 7.5

(ii) Total amount of investment = Number of share × Market value of share
Total amount of investment = 80 × Rs. 60
Total amount of investment = Rs. 4800

Question 19. Rohit invested Rs. 9,600 on Rs. 100 shares at Rs. 20 premium paying 8% dividend. Rohit sold the shares when the price rose to Rs. 160. He invested the proceeds (excluding dividend) in 10% Rs. 50 shares at Rs. 40. Find the:
(i) Original number of shares.
(ii) Sale proceeds.
(iii) New number of shares.
(iv) Change in the two dividends.
Solution :
(i) It is given that,
Nominal value per share = Rs. 100
Premium = 20%
Market value per share = Nominal Value + Premium
Market value per share = Rs. 100 + (Rs. 100 × 20%)
Market value per share = Rs. 100 + Rs. 20
Market value per share = Rs. 120

(ii) Price of share after raise = Rs. 160
Sale proceeds = Number of share × Price of share
Sale proceeds = 80 × Rs. 160
Sale proceeds = Rs. 12,800
(iii) Total Amount of investment = 12,800
Rate of Dividend = 10%
Nominal value per share = Rs. 50
Market value per share = Rs. 40

(iv) Rate of dividend = 10%
Dividend per share = Rs. 50 × 10%
Dividend per share = Rs. 5
Total Dividend = 320 × Rs. 5
Total Dividend = Rs. 1600
Change in total dividend = Rs. 1600 – Rs. 640
Change in total dividend = Rs. 960
Question 20. How much should a man invest in Rs. 50 shares selling at Rs. 60 to obtain an income of Rs. 450, if the rate of dividend declared is 10%. Also find his yield percent, to the nearest whole number.
Solution :
It is given that,
Nominal value per share = Rs. 50
Market value per share = Rs. 60
Rate of Dividend = 10%
Dividend per share = Rs. 50 × 10%
Dividend per share = Rs. 5

Total amount of investment = Number of shares × Market value per share
Total amount of investment = 90 × Rs. 60
Total amount of investment = Rs. 5,400





