Get ICSE Class 10 Mathematics syllabus for your exam. Every student should know the syllabus of a particular subject before attending that exam. To solve this problem, we provide you ICSE Class 10 Mathematics syllabus for your exam.
It is hard to imagine to make preparation for class 10 Mathematics without ICSE Class 10 Mathematics syllabus So if you want to score higher marks in your exam. So, firstly learn the ICSE Class 10 Mathematics syllabus, and then let’s start to practice in class 10 Mathematics.
ICSE Class 10 Mathematics syllabus
1. Commercial Mathematics
(i) Value Added Tax
Computation of tax including problems involving discounts, list-price, profit, loss, basic/cost price
including inverse cases.
(ii) Banking
Recurring Deposit Accounts : computation of interest and maturity value using the formula:

(iii) Shares and Dividends
(a) Face/Nominal value, Market Value, Dividend, Rate of Dividend, Premium.
(b) Formulae
• Income = number of shares × rate of dividend × FV.
• Return = (Income/Investment) × 100.
Note : Brokerage and fractional shares not included.
2. Algebra
(i) Linear Inequations
Linear Inequations in one unknown for x Î N, W, Z, R. Solving
• Algebraically and writing the solution in set notation form.
• Representation of solution on the number line.
(ii) Quadratic Equations in one variable
(a) Nature of roots
• Two distinct real roots if b2 – 4ac > 0
• Two equal real roots if b2 – 4ac = 0
• No real roots if b2 – 4ac < 0
(b) Solving Quadratic equations by:
• Factorisation
• Using Formula.
(c) Solving simple quadratic equation problems.
(iii) Ratio and Proportion
(a) Proportion, Continued proportion, mean proportion.
(b) Componendo, dividendo, alternendo, invertendo properties and their combinations.
(c) Direct simple applications on proportions only
(iv) Factorisation of polynomials:
(a) Factor Theorem.
(b) Remainder Theorem.
(c) Factorising a polynomial completely after obtaining one factor by factor theorem.
Note : f (x) not to exceed degree 3.
(v) Matrices
(a) Order of a matrix. Row and column matrices.
(b) Compatibility for addition and multiplication.
(c) Null and Identity matrices.
(d) Addition and subtraction of 2×2 matrices.
(e) Multiplication of a 2×2 matrix by
• a non-zero rational number
• a matrix.
(vi) Arithmetic and Geometric Progression
• Finding their General term.
• Finding Sum of their first ‘n’ terms.
• Simple Applications.
(vii) Co-ordinate Geometry
(a) Reflection
(i) Reflection of a point in a line : x=0, y =0, x= a, y=a, the origin.
(ii) Reflection of a point in the origin.
(iii) Invariant points.
(b) Co-ordinates expressed as (x,y), Section formula, Midpoint formula, Concept of slope, equation of a line, Various forms of straight lines.
(i) Section and Mid-point formula (Internal section only, co-ordinates of the centroid of a triangle included).
(ii) Equation of a line:
• Slope –intercept form y = mx + c
• Two- point form (y-y1) = m(x-x1)
Geometric understanding of ‘m’ as slope/gradient tanq where q is the angle the line makes with the positive direction of the x axis. Geometric understanding of ‘c’ as the y-intercept/the ordinate of the point where the line intercepts the y axis/ the point on the line where x=0.
• Conditions for two lines to be parallel or perpendicular.
Simple applications of all the above.
3. Geometry
(a) Similarity
Similarity, conditions of similar triangles
(i) As a size transformation.
(ii) Comparison with congruency, keyword being proportionality.
(iii) Three conditions: SSS, SAS, AA. Simple applications (proof not included).
(iv) Applications of Basic Proportionality Theorem.
(v) Areas of similar triangles are proportional to the squares of corresponding sides.
(vi) Direct applications based on the above including applications to maps and models.
(b) Loci
Loci : Definition, meaning, Theorems and constructions based on Loci.
(i) The locus of a point at a fixed distance from a fixed point is a circle with the fixed point as centre and fixed distance as radius.
(ii) The locus of a point equidistant from two intersecting lines is the bisector of the angles between the lines.
(iii) The locus of a point equidistant from two given points is the perpendicular bisector of the line joining the points.
Proofs not required
(c) Circles
(i) Angle Properties
• The angle that an arc of a circle subtends at the center is double that which it subtends at any point on the remaining part of the circle.
• Angles in the same segment of a circle are equal (without proof).
• Angle in a semi-circle is a right angle.
(ii) Cyclic Properties:
• Opposite angles of a cyclic quadrilateral are supplementary.
• The exterior angle of a cyclic quadrilateral is equal to the opposite interior angle (without proof).
(iii) Tangent and Secant Properties:
• The tangent at any point of a circle and the radius through the point are perpendicular to each other.
• If two circles touch, the point of contact lies on the straight line joining their centers.
• From any point outside a circle two tangents can be drawn and they are equal in length.
• If two chords intersect internally orexternally then the product of the lengths of the segments are equal.
• If a chord and a tangent intersect externally, then the product of the lengths of segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.
• If a line touches a circle and from the point of contact, a chord is drawn, the angles between the tangent and the chord are respectively equal to the angles in the corresponding alternate segments.
Note : Proofs of the theorems given above are to be taught unless specified otherwise.
(iv) Constructions
(a) Construction of tangents to a circle from an external point.
(b) Circumscribing and inscribing a circle on a triangle and a regular hexagon.
4. Mensuration
Area and volume of solids – Cylinder, Cone and Sphere.
Three-dimensional solids – right circular cylinder, right circular cone and sphere: Area (total surface and curved surface) and Volume. Direct application problems including cost, Inner and Outer volume and melting and recasting
method to find the volume or surface area of a new solid. Combination of solids included.
Note : Problems on Frustum are not included.
5. Trigonometry
(a) Using Identities to solve/prove simple algebraic trigonometric expressions
sin2 A + cos2 A = 1
1 + tan2 A = sec2A
1+cot2A = cosec2A; 0 £ A £ 90°
(b) Heights and distances: Solving 2-D problems involving angles of elevation and depression using trigonometric tables.
Note: Cases involving more than two right angled triangles excluded.
6. Statistics
Statistics – basic concepts, Mean, Median, Mode. Histograms and Ogive.
(a) Computation of:
• Measures of Central Tendency: Mean, median, mode for raw and arrayed data. Mean*, median class and modal class for grouped data. (both continuous and discontinuous).
• Mean by all 3 methods included:
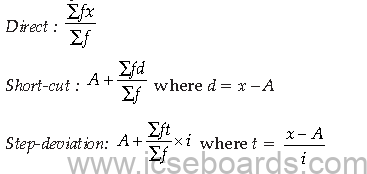
(b) Graphical Representation. Histograms and Less than ogive.
• Finding the mode from the histogram, the upper quartile, lower Quartile and median etc. from the ogive.
• Calculation of inter Quartile range.
7. Probability
• Random experiments
• Sample space
• Events
• Definition of probability
• Simple problems on single events
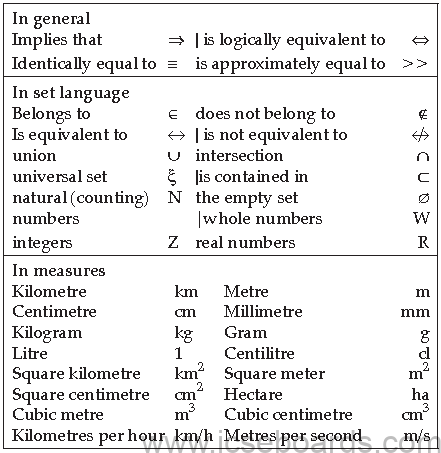
Note: SI units, signs, symbols and abbreviations
(1) Agreed conventions
(a) Units may be written in full or using the agreed symbols, but no other abbreviation may be used.
(b) The letter’s is never added to symbols to indicate the plural form.
(c) A full stop is not written after symbols for units unless it occurs at the end of a sentence.
(d) When unit symbols are combined as a quotient, e.g. metre per second, it is recommended that they be written as
m/s, or as m s-1.
(e) Three decimal signs are in common international use: the full point, the midpoint and the comma. Since the full point is sometimes used for multiplication and the comma for spacing digits in large numbers, it is recommended that the mid-point be used for decimals.
(2) Names and symbols
Internal Assessment
The minimum number of assignments : Two assignments as prescribed by the teacher.
Suggested Assignments
• Comparative newspaper coverage of different items.
• Survey of various types of Bank accounts, rates of interest offered.
• Planning a home budget.
• Conduct a survey in your locality to study the mode of conveyance / Price of various essential commodities/
favourite sports. Represent the data using a bar graph / histogram and estimate the mode.
• To use a newspaper to study and report on shares and dividends.
• Set up a dropper with ink in it vertical at a height say 20 cm above a horizontally placed sheet of plain paper.
Release one ink drop; observe the pattern, if any, on the paper. Vary the vertical distance and repeat. Discover any pattern of relationship between the vertical height and the ink drop observed.
• You are provided (or you construct a model as shown) – three vertical sticks (size of a pencil) stuck to a horizontal board. You should also have discs of varying sizes with holes (like a doughnut). Start with one disc; place it on (in) stick A. Transfer it to another stick (B or C); this is one move (m). Now try with two discs placed in A such that the large disc is below and the smaller disc is above (number of discs = n=2 now). Now transfer them one at a time in B or C to obtain similar situation (larger disc below). How many moves? Try with more discs (n = 1, 2, 3, etc.) and generalise.
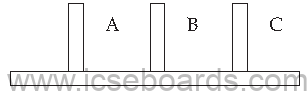
• The board has some holes to hold marbles, red on one side and blue on the other. Start with one pair. Interchange the positions by making one move at a time. A marble can jump over another to fill the hole behind. The move (m) equal 3. Try with 2 (n=2) and more. Find the relationship between n and m.

• Take a square sheet of paper of side 10 cm. Four small squares are to be cut from the corners of the square sheet and then the paper folded at the cuts to form an open box. What should be the size of the squares cut so that the volume of the open box is maximum?
• Take an open box, four sets of marbles (ensuring that marbles in each set are of the same size) and some water. By placing the marbles and water in the box, attempt to answer the question: do larger marbles or smaller marbles occupy more volume in a given space?
• An eccentric artist says that the best paintings have the same area as their perimeter (numerically). Let us not argue whether such sizes increases the viewer’s appreciation, but only try and find what sides (in integers only) a rectangle must have if its area and perimeter are to be equal (note: there are only two such rectangles).
• Find by construction the centre of a circle, using only a 60-30 setsquare and a pencil. l Various types of “cryptarithm”.
Evaluation
The assignments/project work are to be evaluated by the subject teacher and by an External Examiner. (The External Examiner may be a teacher nominated by the Head of the school, who could be from the faculty, but not teaching the subject in the section/class. For example, a teacher of Mathematics of Class VIII may be deputed to be an External Examiner for Class X, Mathematics projects.) The Internal Examiner and the External Examiner will assess the assignments independently.
Award of marks
Subject Teacher (Internal Examiner)
External Examiner
The total marks obtained out of 20 are to be sent to the Council by the Head of the school.
The Head of the school will be responsible for the entry of marks on the mark sheets provided by the Council.
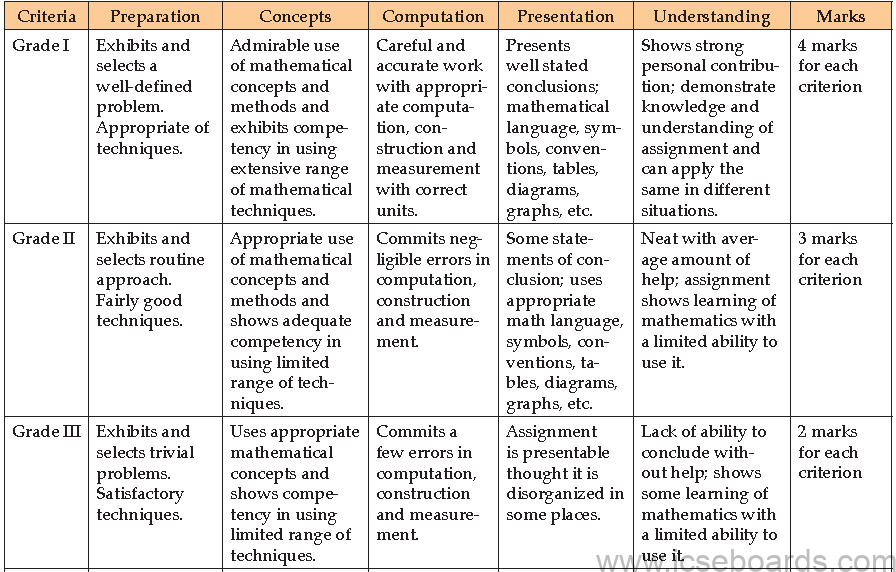
Internal Assessment In Mathematics – Guidelines For Marking With Grades
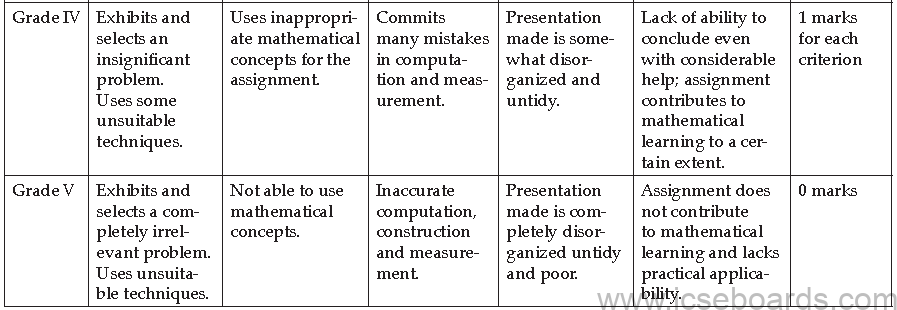

We hope that every student gets ICSE Class 10 Mathematics syllabus before starting the preparation for your exam. You can also check ICSE class 10 Physics syllabus.