Students should refer to ICSE Class 10 Mathematics Question Paper solved Set A given below which will help them to prepare for the upcoming ICSE Mathematics exams. Students should read ICSE Mathematics Class 10 Books to make sure they are completely prepared and should also refer to ICSE Class 10 Mathematics Solutions to understand all questions and their answers.
ICSE Class 10 Mathematics Question Paper solved Set A
Answers to this Paper must be written on the answer sheet provided separately.
You will not be allowed to write during the first 15 minutes.
This time is to be spent in reading the question paper.
The time given at the head of this Paper is the time allowed for writing the answers.
Attempt seven questions in all. Part I is compulsory. All questions from Part I are to be attempted.
A total of five questions are to be attempted from Part II.
The intended marks for questions or parts of questions are given in brackets [ ].
ICSE Class 10 Mathematics Question Paper solved Set A
SECTION – A (40 Marks)
Attempt all the questions from this section.
Question 1
(a) Find the value of ‘x’ and ‘y’ if :

(b) Sonia had a recurring deposit account in a bank and deposited ` 600 per month for 2½ years. If the rate of interest was 10% p.a., find the maturity value of this account. 3
(c) Cards bearing numbers 2, 4, 6, 8, 10, 12, 14, 16, 18 and 20 are kept in a bag. A card is drawn at random from the bag. Find the probability of getting a card which is : 4
(i) a prime number.
(ii) a number divisible by 4.
(iii) a number that is a multiple of 6.
(iv) an odd number.
Answer 1

(c) (i) Prime number = {2}
No. of favourable cards = 1
Total number of cards = 10
Hence, probability of a getting a prime number card = Number of favourable cards / Total no. of cards = 1/10
(ii) Number divisible by 4 = {4, 8, 12, 16, 20}
No. of favourable cards = 5
Hence, probability of a getting card, where number divisible by 4.
= Number of favourable cards / Total no. of cards = 5/10 = 1/2
(iii) Number which are multiple of 6 = {6, 12, 18}
No. of favourable cards = 3
Hence, probability of getting card, which is multiple of 6. = Number of favourable cards / Total No. of cards = 3/10
(iv) Odd number = 0 (No. odd card)
No. of favourable cards = 0
Hence, probability of getting an odd number card = Number of favourable cards / Total No. of cards = 0 / 10 = 0
Question 2
(a) The circumference of the base of a cylindrical vessel is 132 cm and its height is 25 cm. Find the (3)
(i) radius of the cylinder
(ii) volume of cylinder. (use π = 22/7 )
(b) If (k – 3), (2k + 1) and (4k + 3) are three consecutive terms of an A.P., find the value of k. 3
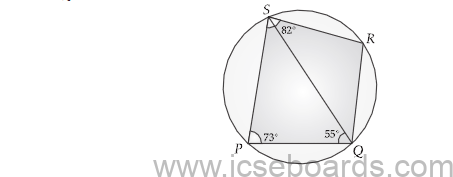
(c) PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate : 4
(i) ∠QRS
(ii) ∠RQS
(iii) ∠PRQ
Answer 2
(a) Given
circumference = 132 cm
height = 25 cm
(i) circumference = 2πr
132 = 2πr
132 =2 × 22 / 7 × r
r = 132 × 7 / 2 × 22 = 21 cm
Hence, radius of cylinder = 21 cm.
(ii) volume of cylinder = πr2h
=22/7 × 21 × 21 × 25
= 34,650 cm3.
(b) For three consecutive terms of an in A.P., the common difference should be same, i.e.
(2k + 1) – (k – 3) = (4k + 3) – (2k + 1)
2k + 1 – k + 3 = 4k + 3 – 2k – 1
k + 4 = 2k + 2
k = 2
(c) Given ∠QPS = 73°, ∠PQS = 55°, ∠PSR = 82°
(i) Since, sum of opposite pairs of angles in cyclic quadrilaterals is 180°
Hence,
∠QRS + ∠QPS = 180°
∠QRS + 73° = 180°
∠QRS = 180° – 73° = 107°
(ii) ∠PQR + ∠PSR = 180° (PQRS is a cyclic quadrilateral)
∠PQR + 82° = 180°
∠PQR = 180° – 82 = 98°
Q ∠PQS + ∠RQS = ∠PQR
55° + ∠RQS = 98°
∠RQS = 98° – 55° = 43°
(iii) Join P to R
In ΔPSQ ∠SPQ + ∠PQS + ∠PSQ = 180°
73° + 55° + ∠PSQ = 180°
∠PSQ = 180° – 128° = 52°
Now,
∠PRQ = ∠PSQ (∵ Q Angle is same segment)
∴ ∠PRQ = 52º

Question 3
(a) If (x + 2) and (x + 3) are factors of x3 + ax + b, find the values of ‘a’ and ‘b’. (3)
(b) Prove that √(sec2θ + cosec2θ) = tanθ + cotθ (3)
(c) Using a graph paper draw a histogram for the given distribution showing the number of runs scored by 50 batsmen. Estimate the mode of the data : (3)

Answer 3
(a) x3 + ax + b
(x + 2) is a factor of given polynomial then x = – 2 will satisfy the polynomial
(– 2)3 + a(– 2) + b = 0
– 8 – 2a + b = 0
b – 2a = 8 …(i)
(x + 3) is also a factor of given polynomial then x = – 3 will satisfy the polynomial
(– 3)3 + a(– 3) + b = 0
– 27 – 3a + b = 0
b – 3a = 27 …(ii)
On solving (i) and (ii), we get
a = – 19, b = – 30


Question 4
(a) Solve the following inequation, write down the solution set and represent it on the real number line : (3)
– 2 + 10x ≤ 13x + 10 < 24 + 10x, x ∈ Z
(b) If the straight lines 3x – 5y = 7 and 4x + ay + 9 = 0 are perpendicular to one another, find value of a. (3)
(c) Solve x2 + 7x = 7 and give your answer correct to two decimal places. (4)
Answer 4
(a) – 2 + 10x ≤ 13x + 10 < 24 + 10x
or – 2 ≤ 3x + 10 < 24
or – 12 ≤ 3x < 14
or – 4 ≤ x < 14/3
or – 4 ≤ x < 4(2/3)
∴ The solution set is x ∈ [– 4, 4] and x ∈ Z

(c) x2 + 7x = 7
x2 + 7x – 7 = 0
Compare the equation to
ax2 + bx + c = 0
a = 1, b = 7, c = – 7
D = b2 – 4ac
= (7)2– 4 × 1 × (– 7)
= 49 + 28
= 77
Roots are real, different and irrational number,

ICSE Class 10 Mathematics Question Paper solved Set A
SECTION- B (40 Marks)
Attempt any four questions from this Section
Question 5
(a) The 4th term of a G.P. is 16 and the 7th term is 128. Find the first term and common ratio of the series. (3)
(b) A man invests ₹ 22,500 in ₹ 50 shares available at 10% discount. If the dividend paid by the company is 12%, calculate : (3)
(i) The number of shares purchased
(ii) The annual dividend received.
(iii) The rate of return he gets on his investment. Give your answer correct to the nearest whole number.
(c) Use graph paper for this question (Take 2 cm = 1 unit along both x and y axis). (4)
ABCD is a quadrilateral whose vertices are A(2, 2), B(2, – 2), C (0 – 1) and D(0, 1)
(i) Reflect quadrilateral ABCD on the y-axis and name it as A’B’CD.
(ii) Write down the coordinates of A’ and B’.
(iii) Name two points which are invariant under the above reflection.
(iv) Name the polygon A’B’CD.
Answer 5
(a) Given, T4 = 16 and T7 = 128
Let First term of G.P. be a and common ratio be r.
so T4 = ar3 = 16 ….(i)
T7 = ar6 = 128 …(ii)
Dividing (ii) by (i), we get
ar6 / ar3 = 128/16
r3 = 8
r = 2
From (i)
a.(2)3 = 16
a × 8 = 16
a = 2
(b) Given,
Total investment = ₹ 22,500, Face value = ₹ 50
Market value = ₹ ( 50 – 10/100 x 50 ) = ₹ 45 (∵ 10% discount)
Dividend = 12%
(i) No. of Shares = Investment / Market value of share
= 22500 / 45 = 500
(ii) Annual dividend = No. of shares × Nominal value of share × dividend rate
= 500 × 50 × 12/100
= ₹ 3000
(iii) Return percentage = Total dividend / Total investment × 100
= 3000 / 22500 × 100
= 13.3% = 13%

(ii) Co-ordinates of A’ → (– 2, 2)
Co-ordinates of B’ → (– 2, – 2)
(iii) Two invariant points are C(0, – 1) and D(0, 1)
(iv) A’B’CD is a trapezium quadrilateral
Question 6
(a) Using properties of proportion, solve for x. Given that x is positive : (3)

(c) Prove that (1 + cotθ – cosecθ)( 1+ tanθ + secθ) = 2 (4)
Answer 6


Question 7
(a) Find the value of k for which the following equation has equal roots. (3)
x2 + 4kx + (k2 – k + 2) = 0
(b) One map drawn to a scale of 1 : 50,000, a rectangular plot of land ABCD has the following dimensions.
AB = 6 cm ; BC = 8 cm and all angles are right angles. Find : (3)
(i) the actual length of the diagonal distance AC of the plot in km.
(ii) the actual area of the plot in sq km.
(c) A(2, 5), B(– 1, 2) and C(5, 8) are the vertices of a triangle ABC, ‘M’ is a point on AB such that AM : MB = 1 : 2.
Find the co-ordinates of ‘M’. Hence find the equation of the line passing through the points C and M. (4)
Answer 7
(a) x2 + 4kx + (k2 – k + 2) = 0
Compare the equation to
ax2 + bx + c = 0
a = 1, b = 4k, c = k2 – k + 2
Since roots of the equation are equal
b2 – 4ac = 0
(4k)2 – 4 × 1 × (k2 – k + 2) = 0
16k2 – 4k2 + 4k – 8 = 0
12k2 + 4k – 8 = 0
3k2 + k – 2 = 0
3k2 + 3k – 2k – 2 = 0
3k (k + 1) – 2(k + 1) = 0
(k + 1) (3k – 2) = 0
k = – 1, k = 2/3
(b) (i) Since, AB = 6 cm
BC = 8 cm
By Pythagorean theorem
Diagonal AC = √AB2+BC2
= √(6)2 + (8)2
= 100 = 10 cm
Since, it is given that 1 cm = 50,000 cm (1 : 50000)
∴ 10 cm = 5,00,000 cm
Diagonal AC = 5 km
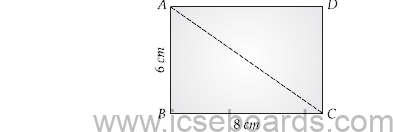
(ii) Area = AB × BC
= 6 × 8
= 48 cm2
= 48 × (50,000 × 50,000) [1 km2 = 10,00,00,00,000 cm2]
= 1,20,00,00,00,000 cm2
= 12 sq. km
(c) Let M (x1, y1) be the point which divides the line segment AB in the ratio 1 : 2
Hence, Coordinate of M are
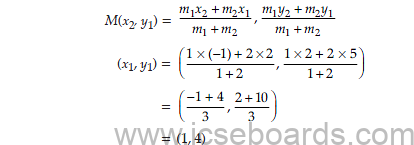
Coordinates of M are (1, 4)
Now equation of line passing through C(5, 8) and M(1, 4) is
y – 8 = 4 – 8 / 1 – 5 (x − 5)
y – 8 = −4 / -4 (x 5)
y – 8 = x – 5
y = x + 3
Question 8
(a) ₹ 7500 were divided equally among a certain number of children. Had there been 20 less children, each would have received ₹ 100 more. Find the original number of children. (3)
(b) If the mean of the following distribution is 24, find the value of ‘a’. (3)

(c) Using ruler and compass only, construct a ΔABC such that BC = 5 cm and AB = 6.5 cm and ∠ABC = 120°. (4)
(i) Construct a circum-circle of ΔABC
(ii) Construct a cyclic quadrilateral ABCD, such that D is equidistant from AB and BC.
Answer 8
(a) Let the number of children be x and ` y is given to each children then
x.y = 7,500 …(i)
and (x – 20) (y + 100) = 7,500
xy + 100x – 20y – 2,000 = 7,500
7,500 + 100x – 20y – 2,000 = 7,500 [∵ xy = 7,500]
100x – 20y – 2,000 = 0
100x – 20 × (7,500 / x) – 2,000 = 0 [From (i) y = 7,500/x]
100 x2 – 1,50,000 – 2,000 x = 0
x2 – 20x – 1,500 = 0
x2 – 50x + 30x – 1,500 = 0
x (x – 50) + 30 (x – 50) = 0
(x – 50) (x + 30) = 0
x = 50, – 30
The number of children can not be – ve.
x = 50
∴ Number of children = 50

x= ∑ƒixi / ∑ƒi
24 = 810 + 15a / 30 + a
720 + 24a = 810 + 15a
24a – 15a = 810 – 720
9a = 90
a = 10
(c) (a) Steps of construction :
(i) Draw a line segment BC = 5 cm.
(ii) Construct ∠ABC = 120°.
(iii) Cut BA = 6.5 cm
(iv) Join A to C.
(v) Construct perpendicular bisectors of AB and BC, intersecting at O. Join AO
(vi) Taking O as centre, and OA as radius draw a circle, passing through A, B and C.
(b) (i) Draw the bisector of ∠ABC such that it touches the circle at point D.
(ii) Join A to D and C to D.
(iii) ABCD is required cyclic quadrilateral.

Question 9
(a) Priyanka has a recurring deposit account of ₹ 1000 per month at 10% per annum. If she gets ₹ 5550 as interest at the time of maturity, find the total time for which the account was held. (3)
(b) In ΔPQR, MN is parallel to QR and PM/MQ = 2/3
(i) Find MN/QR
(ii) Prove that ΔOMN and ΔORQ are similar.
(iii) Find, area of ΔOMN : Area of ΔORQ

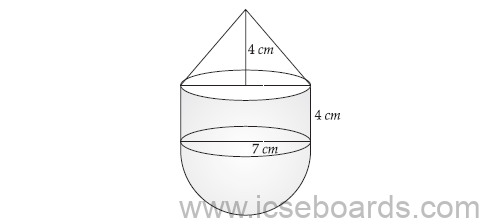
(c) The following figure represents a solid consisting of a right circular cylinder with a hemisphere at one end and a cone at the other. Their common radius is 7 cm. The height of the cylinder and cone are each of 4 cm. Find volume of the solid.
Answer 9
(a) P = ₹ 1,000, R = 10%, p.a., S.I.= ₹ 5,550
n = ?
SI = Pn(n + 1) / 2 × 1/12 × R/100
5,550 = 1000 × n (n + 1) × 10 / 2 × 12 × 100
n(n + 1) = 1332
n2 + n – 1332 = 0
n2 + 37n – 36n – 1332 = 0
n(n + 37) – 36 (n + 37) = 0
(n + 37)(n – 36) = 0
n = 36, – 37
The value of time can not be – ve, Hence
n = 36 months
or n = 3 years
(i) Given MN||QR, then
or ∴ PM/PQ = MN/QR (By Thales theorem)
or 2 / PM+MQ = MN/QR
or 2 / 2+3 = MN/QR
⇒ MN/QR = 2/5
(ii) MN ||QR (Given)
∠OMN = ∠ORQ (Alternate angle)
∠ONM = ∠OQR (Alternate angle)
∠MON = ∠ROQ (Vert. Opp. angles)
∴ ΔOMN ~ ΔORQ (by AAA similarity)
(iii) ∵ ΔOMN and ΔORQ are similar triangle
We know that ratio of the areas of two similar triangle is equal to ratio of the squares of the corresponding sides.
∴ ar (ΔOMN)/ar (ΔORQ) = MN2 / QR2
= (MN/QR)2 = (2/5)2
= 4/25
Hence, ar (ΔOMN) : ar (ΔORQ) = 4 : 25
common radius (r) = 7 cm
Height of cylinder = height of cone
= h = 4 cm
volume of solid = volume of hemisphere + volume of cylinder + volume of cone
= 2/3πr3 + πr2h + 1/3πr2h
= 2/3π×7×7×7+π×7×7×4+1/3×π×7×7×4
= 686π / 3 + 196π + 196π / 3
= 686π+588π+196π / 3
= 1,470π / 3 = 490π cm3
Question 10
(a) Use Remainder theorem to factorize the following polynomial : (3)
2x3 + 3x2 – 9x – 10.
(b) In the figure given below ‘O’ is the centre of the circle. If QR = OP and ∠ORP = 20°. Find the value of ‘x’ giving reasons. (3)

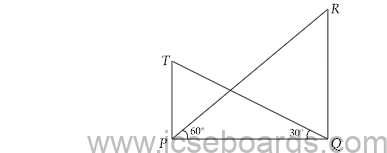
(c) The angle of elevation from a point P of the top of a tower QR, 50 m high is 60° and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre. (4)
Answer 10
(a) Let ƒ(x) = 2x3 + 3x2 – 9x – 10
the factors of the constant terms are ± 1, ± 2, ± 5 and ± 10.
We have
ƒ(–1) = 2(–1)3 + 3(–1)2 – 9(– 1) – 10
= – 2 + 3 + 9 – 10
= 0
So, (x + 1) is a factor of ƒ(x)
Let, we now divide ƒ(x) = 2x3 + 3x2 – 9x – 10 by (x + 1) to get the other factor of ƒ(x)

∴ 2x3 + 3x2 – 9x – 10 = (x+ 1) (2x2 + x – 10)
= (x + 1)[2x2 + 5x – 4x – 10]
= (x + 1) [x(2x + 5) – 2(2x + 5)]
= (x + 1) (x – 2) (2x + 5)
(b) Given QR = OP …(i)
and ∠ORP = 20°
∵ ∠ORQ = ∠ORP = 20°
∵ OP = OQ (Radius of the circle)
∴ QR = OQ (From (i))
In ΔOQR :
∵ OQ = QR
∴ ∠QOR = ∠ORQ
= 20°
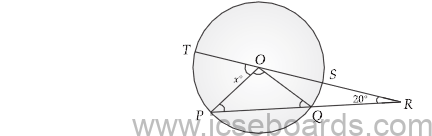
Now ∠OQR + ∠ORQ + ∠QOR = 180° (By angle sums property)
∠OQR + 20° + 20° = 180°
∠OQR = 180° – 40°
= 140°
Now ∠OQR + ∠OQP = 180° (By linear pair)
140° + ∠OQP = 180°
∠OQP = 180° – 140°
= 40°
In ΔPOQ
∵ OP = OQ
∴ ∠OPR = ∠OQP = 40°
Now ∠POQ + ∠OPR + ∠OQP = 180° (By angle sum property)
∠POQ + 40° + 40° = 180°
∠POQ = 180° – 80°
= 100°
Now
∠ROQ + ∠POQ + x = 180° (By Linear pair)
20° + 100° + x = 180°
x = 180° – 120°
x = 60°
(c) Let the height of the tower PT be h and distance PQ = xm
In ΔPRQ
tan 60° = RQ/PQ
√3 = 50/x
or x = 50/√3
In right ΔPTQ,
tan 30° = PT/PQ = h/x
1/√3 = h / (50 / √3)

3h = 50
h = 50/3 = 16.66 = 17 m
Question 11
(a) The 4th term of an A.P. is 22 and 15th term is 66. Find the first term and the common difference. Hence find the sum of the series to 8 terms. (4)
(b) Use Graph paper for this question. (6)
A survey regarding height (in cm) of 60 boys belonging to Class 10 of a school was conducted. The following data was recorded :

Taking 2 cm = height of 10 cm along one axis and 2 cm = 10 boys along the other axis draw an ogive of the above distribution. Use the graph to estimate the following :
(i) the median
(ii) lower quartile
(iii) if above 158 cm is considered as the tall boys of the class. Find the number of boys in the class who are tall.
Answer 11
(a) Let first term be a and common difference be d.
T4 = a + 3d = 22, …(i)
T15 = a + 14d = 66 …(ii)
Subtracting (ii) from (i)
a + 14d – a – 3d = 66 – 22
11d = 44
d = 4
From (i)
a + 3 × 4 = 22
a = 22 – 12
= 10
Thus, S8 = 8/2 [2 × 10 + (8 – 1) 4]
= 4 [20 + 28]
= 4 × 48
= 192


Here, n = 60
(i) Median = 60/2 term = 30th term = 149.5
(ii) Lower quartile = 60/4 term = 15th term = 145.5
(iii) The number of boys in the class, where height is above 158 cm.
= 60 – 50
= 10