Students should refer to Refraction of Light ICSE Class 10 Physics notes provided below designed based on the latest syllabus and examination pattern issued by ICSE. These revision notes are really useful and will help you to learn all the important and difficult topics. These notes will also be very useful if you use them to revise just before your Physics Exams. Refer to more ICSE Class 10 Physics Notes for better preparation.
ICSE Class 10 Physics Refraction of Light Revision Notes
Students can refer to the quick revision notes prepared for Chapter Refraction of Light in Class 10 ICSE. These notes will be really helpful for the students giving the Physics exam in ICSE Class 10. Our teachers have prepared these concept notes based on the latest ICSE syllabus and ICSE books issued for the current academic year. Please refer to Chapter wise notes for ICSE Class 10 Physics provided on our website.
Refraction of Light ICSE Class 10 Physics
Ben was surprised to see a lemon appear larger than its size when he placed it in a glass filled with water.
What is the reason behind this?

When a light ray travels from one transparent medium to another, it bends at the surface that separates the two media. Hence, the lemon appears larger than its actual size. This happens because different media have different optical densities.
The phenomenon of bending of light as it travels from one medium to another is known as refraction of light.
The phenomenon of refraction shows that the speed of light is different in different media.
As a ray of light moves from an optically rarer medium to an optically denser medium, it bends towards the normal at the point of incidence. Therefore, the angle of incidence
(i) is greater than the angle of refraction (r). Hence, i > r.

As a ray of light moves from an optically denser medium to an optically rarer medium, it bends away from the normal. Therefore, the angle of incidence
(i) is less than the angle of refraction (r). Hence, i < r.
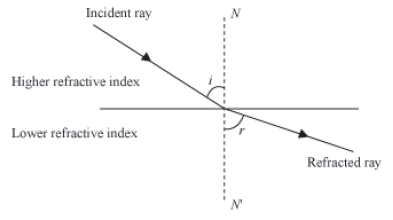
Partial reflection and refraction of light at the boundary of two medium
Case I: Refraction from rarer to denser medium

When light travels from rarer to denser medium, suppose from air to glass, the partially refracted light bends towards the normal and partially reflected light returns back into the same medium.
Case II: Refraction from denser to rarer medium
When light travels from denser to rarer medium, suppose from glass to air, the partially refracted light bends away from the normal and partially reflected light returns back into the same medium.
Effect on various characteristics of light on reflection and refraction:

Speed of Light
Light changes its speed when it enters one medium from another. The velocities of light in various media are given in the following table.
| Medium | Velocity |
| Air | 3 × 108 m/s |
| Water | 2.25 × 108 m/s |
| Glass | 1.8 × 108 m/s |
From the table, we can easily see that light travels with lesser speed through glass and water than it does through air. Therefore, we can say that water and glass are optically denser than air, or air is optically rarer than water and glass.
Refraction of light occurs because of this change in the speed of light due to a change in the medium. When light enters an optically denser medium from an optically rarer medium, the speed of light slows down and light bends towards the normal. The opposite happens when light enters an optically rarer medium from an optically denser
medium.
The extent of bending of light depends on the refractive index of the medium. Refractive index (μ) of a medium is defined as the ratio of the speed of light in vacuum to that in the medium.
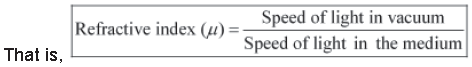
Therefore, an optically denser medium has a higher refractive index than an optically rarer medium. So, we can say that the refractive index of water is higher than that of air.
Factors affecting refracting index of a medium:
• Nature of the medium
• Temperature of the medium
• Wavelength of the light used
Grasshopper−Frog Relation

Consider a situation where a frog is sitting inside a pond (refractive index μ2), while a grasshopper is sitting on a bush slightly above in air (refractive index μ1), as shown in the given figure.
Two situations arise in this case.
Situation I
The grasshopper is looking towards the frog.

Situation II

The frog is looking towards the grasshopper. In this case, light is travelling from a denser to a rarer medium as the refractive index of water (μ2) is greater than that of air (μ1). Therefore, light will bend away from the normal. Hence, the grasshopper appears farther to the frog.
Refraction Through Glass Slab
Laws of refraction
There are two laws of refraction.
First law of refraction
The incident ray, the refracted ray, and the normal to the interface of two media at the point of incidence – all lie in the same plane.
Second law of refraction
The ratio of the sine of the angle of incidence to the sine of the angle of refraction is constant, for the light of a given color and for given pair of media. This is known as Snell’s law. Mathematically, it can be given as follows:

Here,”aμb is the relative refractive index of medium b with respect to medium a.
Conditions for light ray to pass undeviated on refraction
• The angle of incidence of light ray at the edge of two media should be zero degree
• The refractive index of the two medium should be same
If any one of the above two conditions fulfils, then the ray of light will pass undeviated on travelling from one medium to another.
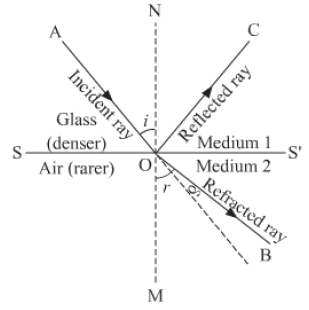
Principle of reversibility of path of light
Principle of reversibility states that the path of a ray of light is reversible. When a light ray AO travelling from rarer (medium 1) to denser medium (medium 2) is incident at an angle i to the surface separating the two media, it gets refracted along OB making an angle r with the normal to the surface. Thus, the refractive index of medium 2 w.r.t.
medium 1 is
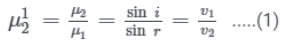
where v1 and v2 is the speed of light in medium 1 and medium 2, respectively.
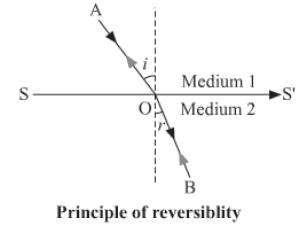
Similarly, if the light ray travels from denser to rarer medium along BO and incidents at the surface at an angle r, then it is going to get refracted only along the direction OA making an angle i with the normal in medium 1 and in no other direction than OA. Thus, the refractive index of medium 1 w.r.t. medium 2 is

So, what are the key points of the experiment?
• When a light ray enters from air (rarer medium) to glass (denser medium), it bends towards the normal.
• When a light ray emerges from the glass (denser medium) to air (rarer medium), it bends away from the normal.
Since refraction occurs at two parallel surfaces RS and PQ, therefore angle i1 = r2 by the principle of reversibility of the path of the light ray. Hence, when a light ray is
incident on a rectangular glass slab, the light ray emerges parallel to the incident ray from the opposite side of the slab.
Interestingly, when a light ray is incident on a glass slab normally, it gets out straight without any deflection i.e., i = 0, r = 0.
Lateral Displacement

The path of the incident ray AO in the absence of glass block has been shown in the above figure by dotted line OD. Now, the incident ray AO is parallel to the emergent ray BC and is going in the same direction but not along the same line. It means emergent ray has been displaced by the rectangular glass slab. And the shortest distance between the path of emergent ray BC and the direction of incident ray OD is known as lateral displacement (here XY).
The lateral displacement is
• directly proportional to angle of incidence
• directly proportional to the thickness of the block or medium
• directly proportional to the refractive index of the medium. As refractive index increases
with decrease in wavelength of light, this means lateral displacement increases with decrease in the wavelength of light.
Multiple images in a thick plane glass plate or thick mirror
When an illuminated object is placed in front of a plane glass mirror of adequate thickness and is viewed obliquely, a number of images are seen. And from all the images, the second image is the brightest, while rest are of decreasing brightness.
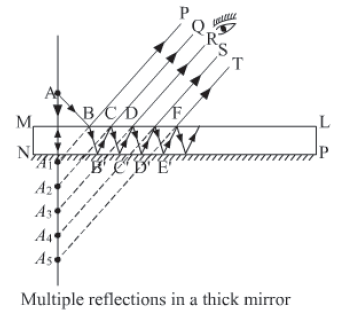
Considering two rays from object A falls on the glass mirror MNPL. One ray is falling normally (AM) and the other ray (AB) obliquely on the given mirror. Now a small part of light ray AB is reflected in the direction of BP and forms a virtual image at A1, while larger part of light is refracted along BB’ inside the glass mirror.
The ray BB’ which strikes at B’, is now strongly reflected back by the silvered surface PN inside the glass as B’C. Again, the ray is then partially refracted along CQ in air and partially reflected along CC’ within the glass. The refracted ray CQ forms the virtual image A2. The image A2 is the brightest image because it is due to the light suffering a strong first reflection at the silvered surface PN.
In the similar manner, the ray CC’ suffers multiple reflections at C’, D, D’ and so on and undergoes refractions at D, E, F and so on within the thickness of glass slab and thus give rise to multiple virtual images A3, A4, A5 and so on of gradually decreasing brightness.
Effects of Refraction
Refraction shows various effects in everyday life. Some of these effects are explained as under.
1. Real and Apparent Depth
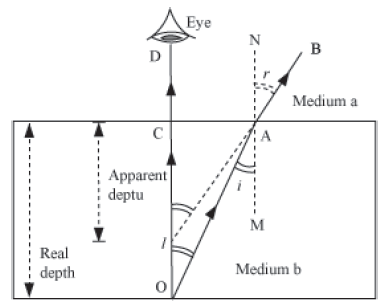
Real depth — the actual depth at which object is situated is called real depth.
Apparent depth — the depth at which image of the object is formed is called apparent depth.
As we can see in the figure that ‘b’ is denser medium than a thus the image formed is above the position of the object.

2. Bending of Stick

On the similar principle of refraction we see the stick bend and shorten when immersed in water.
3. Twinkling of stars

4. Raised beaker bottom
Stars appear to twinkle due to refraction at various layers of the atmosphere.

5. Early sunrise and delay sunset
Sun appears a few minutes earlier before it actually rises above the horizon. Also, it is seen for a few minutes longer after it actually sets. The cause of these two phenomena is the atmospheric refraction.
The layers near the Earth’s surface are denser than those above. So, when the Sun is just below the horizon, the light ray coming from it, suffers refraction from a rarer to denser medium causing the light ray to bend towards the normal at each refraction. Due to this continuous bending of light rays, we are able to see the Sun even when it is actually below the horizon.

Refraction Through a Prism
Prism
A transparent refracting medium which is bounded by five plane surfaces and having a triangular cross section is known as prism.

The figure below shows the passage of light through a triangular prism ABC.

The angles of incidence and refraction at first face AB are ∠i and ∠r1.
The angle of incidence at the second face AC is ∠r2 and the angle of emergence ∠e.
δ is the angle between the emergent ray RS and incident ray PQ and is called the angle of deviati
on. Here, ∠PQN = i
∠SRN’ = e
∠RQO = r1
∠QRO = r2
∠KTS = δ
∴ ∠TQO = i and ∠RQO = r1, we have
∠TQR = i − r1
∠TRO = e and ∠QRO = r2
∠TRQ = e − r2
In triangle TQR, the side QT has been produced outwards. Therefore, the exterior angle δ should be equal to the sum of the interior opposite angles.
i.e, δ= ∠TQR + ∠TRQ = (i − r1) + (e − r2)
δ = (i + e) − (r1+ r2) …(i)
In triangle QRO,
r1+ r2+ ∠ROQ = 180° …(ii)
From quadrilateral AROQ, we have the sum of angles (∠AQO + ∠ARO = 180°). This means that the sum of the remaining two angles should be 180°.
i.e , ∠A + ∠QOR = 180° [∠A is called the angle of prism]
From equations (i) and (ii),
r1+ r2 = A (iii)
Substituting (iii) in (i), we obtain
δ = (i + e) − A
A+δ=i+eA+δ=i+e
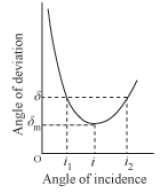
If the angle of incidence is increased gradually, then the angle of deviation first decreases, attains a minimum value (δm), and then again starts increasing.
When angle of deviation is minimum, the prism is said to be placed in the minimum deviation position.
There is only one angle of incidence for which the angle of deviation is minimum.
When
δ = δm [prism in minimum deviation position],
e = i and r2 = r1 = r …(iv)
∵ r1 + r2 = A
From equation (iv), r + r = A
r = A/2
Also, we have
A + δ = i + e
Setting,
δ = δm and e = i
A + δm = i + i
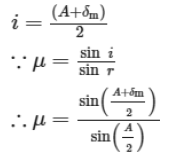
Factors affecting angle of deviation
• Angle of incidence (i)
• Angle of prism (A)
• Refractive index (μμ) of the material of the prism
• Colour or wavelength (λλ) of light

Total internal reflection is the phenomenon of reflection of light into a denser medium from an interface of the denser medium and the rarer medium.
Two essential conditions for total internal reflection:
• Incident ray should travel in the denser medium and refracted ray should travel in the rarer medium.
• Angle of incidence (i) should be greater than the critical angle for the pair of media in contact.
Relation between refractive index and critical angle (C):
When, i = C and r = 90°:
Applying Snell’s law at A2,
μb sin C = μa sin 90° = μa × 1

Some applications of total internal reflection:
• Brilliance of diamond − The critical angle for diamond-air interface is 24.4°. The diamond is cut suitably, so that light entering the diamond from any face falls at an angle greater than 24.4°, suffers multiple total internal reflections at the various faces and remains within the diamond. Hence, the diamond sparkles.
• Mirage → It is an optical illusion in which an object, such as a tree, appears to be inverted.
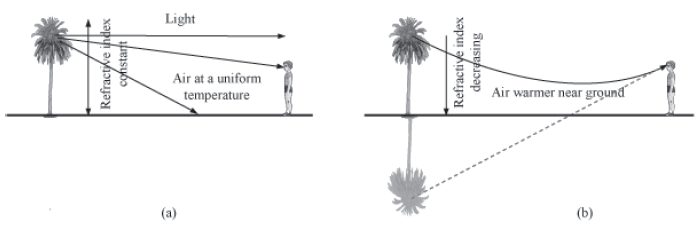
This happens due to uneven heating of the different layers of air due to which density and refractive index of air go on increasing slightly with height above the surface of the earth.
As a result of this, light from a tall object, such as a tree, passes through a medium whose refractive index decreases towards the ground. Thus, a ray of light undergoes total internal reflection. To a distant observer, the light appears to be coming from somewhere below the ground.
Total internal reflection through prism − When a ray of light falls normally on one of the surfaces of a right angled isosceles prism or an equilateral prism, then it is able to totally reflect the light ray internally.
Case I: Total internal reflection through an isosceles right angled prism: The prism can be used
(1) to deviate a ray of light through 90°
(2) to bend a ray of light through 180°
(3) to erect an inverted image without producing a deviation in its path
(1) Deviation of light ray through 90 degrees:

A total reflecting prism ABC is used for deviating light through 90 degrees. A ray of light incident normally on the face AB, passes un-deviated into the prism and strikes the face AC at angle of incidence of 45 degrees. Now, the light suffers total internal reflection at face AC because the incidence angle is greater than the critical angle (for glass-air
interface, critical angle is approximately equal to 42 degrees).
Now, the reflected beam inside the prism strike the face BC normally and therefore passes undeviated. Hence, the incident ray gets deviated by 90 degrees.
(2) Deviation of light ray through 180 degrees:
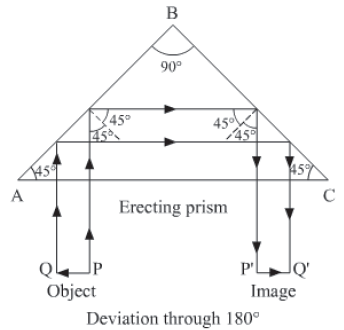
In this case, when an object is placed in front of face AC, the incident rays fall normally on it and enter the prism un-deviated. Now, these rays incident on face AB at an angle of incidence of 45 degrees greater than critical angle of glass-air interface and suffer total internal reflection. The reflected beam inside the prism strikes the face BC with an angle of incidence equal to 45 degree greater than the critical angle and again suffers total internal reflection.
The beam now falls normally on the face AC and therefore passes un-deviated out of the prism, forming an image P’Q’ of the object PQ. Hence, the incident ray gets deviated by 90 degrees at each reflection and therefore total deviation due to two reflection becomes 180 degrees.
(3) Erection of inverted image without deviating path of light ray:
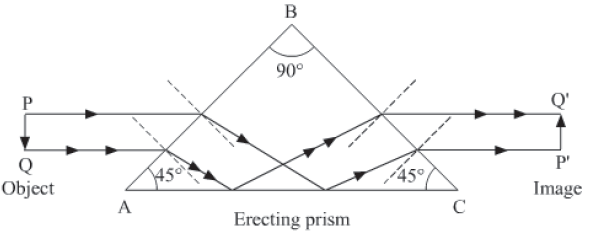
Here, the incident beam of an object PQ falls parallel to the face AC. It bends towards the normal at the air-glass interface AB and strikes the face AC of the prism. The incident angle of the beam at face AC is 45 degrees which is greater than the critical angle of the glass-air interface and thus the beam suffers total internal reflection at this
face.
The totally reflected beam strikes the face BC at an angle less than the critical angle of glass-air interface and bends away from the normal at the interface. Hence, the beam emerges parallel to face AC as result of refraction. On emergence, the rays coming from the object PQ get inverted and thus an erect image P’Q’ is obtained for PQ.
Case II: Total internal reflection through an equilateral prism: In this case, the incident ray bends through an angle of 60 degrees from its initail direction. This is shown in the figure below.
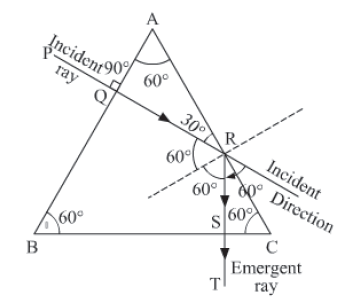
• Optical fibres – Optical fibres consist of thousands of very long thin fibres of fine quality glass or quartz. The central part of the fibres is made up of material with refractive index 1.7; it is called core.The fibres are coated with a material of refractive index 1.5
called cladding. Thus, the core is denser then the cladding.
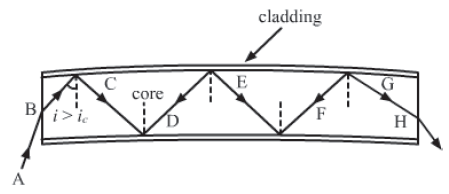
Working:
When a ray of light is incident at one end of the fibre, it undergoes repeated total internal reflection inside the fibre. The only condition is that the light must be incident on the wall of the fibre at an angle greater then the critical angle. Thus, light finally comes out at the other end of the fibre without any loss in intensity.
Uses:
• Optical fibres are extensively used for transmitting audio and video signals through long distances.
• They are used in endoscopes for medical examinations of inner parts of the body of a patient.
Refraction of Light by Spherical Lenses (Concave And Convex)
Ankit went to an optician and noticed different types of spectacles there. He observed that while the glasses of some spectacles were relatively thicker in the middle, other glasses were thicker on the edge. The glasses of these spectacles are examples of lenses.
A lens is a transparent material bound by two curved surfaces. Lenses are broadly classified into two categories depending on their surfaces.

However, we will discuss only double spherical lenses here.
Convex lens
A convex lens is made by joining two spherical surfaces in such a way that it is thicker at the centre. Its thickness gradually reduces as we move towards the edge.
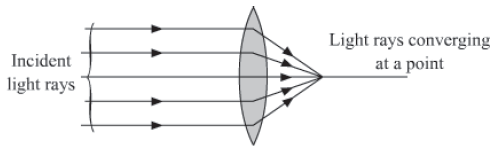
A convex lens has the ability to converge the light rays to a point that are incident on it. Thus, it is called a converging lens.
Concave lens
A concave lens is made by joining two curved surfaces in such a way that it is thinner at the centre. Its thickness gradually increases as we move towards the edge.
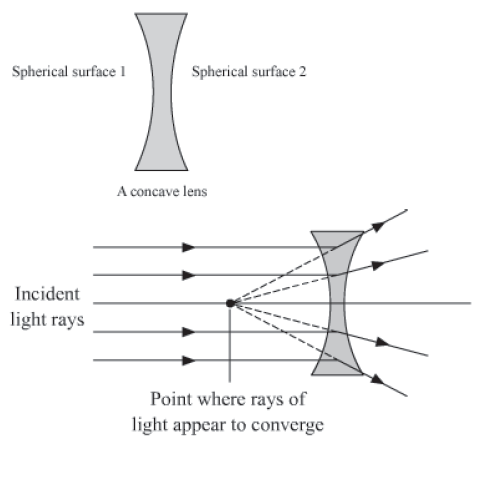
A concave lens has the ability to diverge a beam of light rays incident on it. Thus, it is called a diverging lens.
Differences between a spherical mirror and a lens
The following table lists some common differences between spherical mirrors and lenses
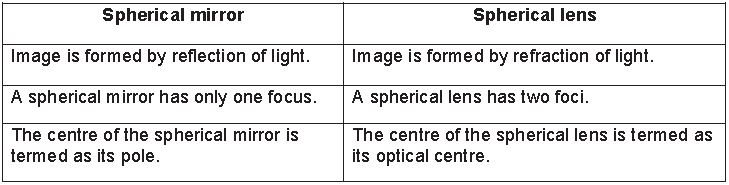
The second difference arises due to the fact that a lens has two spherical surfaces (i.e. it can be made from the arc of two spheres of equal radius).Therefore, light is refracted twice before it comes out of the lens.
Terms Associated with Lenses:

Optical centre
Optical centre is a point at the centre of the lens. It always lies inside the lens and not on the surface. It is denoted by ‘O’.
Centre of curvature
It is the centre point of arcs of the two spheres from which the given spherical lens (concave or convex) is made. Since a lens constitutes two spherical surfaces, it has two centers of curvature.
The distance of the optical centre from either of the centre of curvatures is termed as the radius of curvature.

Principal axis
The imaginary straight line joining the two centers of curvature and the optical
centre (O) is called the principal axis of the lens.

Hold a convex lens and direct it against the sunlight. You will find a bright spot appear on the wall. Can you explain the formation of this bright spot? Light, after refracting through the lens, converges at a very sharp point. Try to obtain the brightest possible spot. Now, place a paper on the wall and observe what happens in the next few minutes.
Focus
The focus (F) is the point on the principal axis of a lens where all incident parallel rays, after refraction from the lens meet or appear to diverge from. For lenses there are two foci (F1 and F2) depending on the direction of incident rays.


The distance between the focus (F1 or F2) and the optical centre (O) is known as the focal length of the lens.
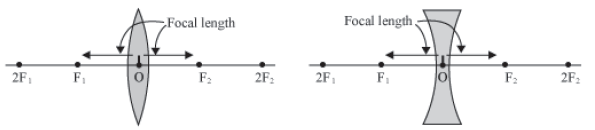
Refraction by Spherical Lenses
Refraction by a spherical lens can be categorized into three cases.
Case I. When the incident light ray is parallel to the principal axis
In this case, the refracted ray will pass through the second focus F2 for a convex lens, and appear to diverge from the first focus F1 for a concave lens.

Case II. When the incident light ray emerges from the first focus F1 of a convex lens, or appears to emerge from the second focus F2 of a concave lens
In this case, light after refraction from both the lenses will move parallel to the principal axis.

Case III. When the light ray passes through the optical centre (O) of a lens
In this case, the light ray will pass through both the lenses without suffering any deviation.

Image Formed by Spherical Lenses

Take a convex lens of known focal length. Draw five equidistant points on a table and put the lens
on the central line. Mark the lines as 2F1, F1, O, F2, 2F2 (as shown in the figure).
Take a candle and placed it behind 2F1. Observe
the nature and size of the image formed on a screen placed on the other side of the lens. An inverted image of the candle flame can be seen easily. Now, repeat the process by changing the position of the candle by bringing it towards the lens, and list your observations.
Lenses are able to form images by refracting incident light rays. Although, a light source emits infinite number of light rays in all possible directions, we will consider only two light rays for the sake of convenience. It allows us to show clearly the nature and position of the image formed on a screen.
Images Formed by a Convex Lens
A convex lens can produce real as well as virtual images. The nature of the images formed depends primarily on the position of the object on the principal axis.
Consider the following cases:
The ray diagrams for all the cases are as follows:
I. When the object is at infinity.
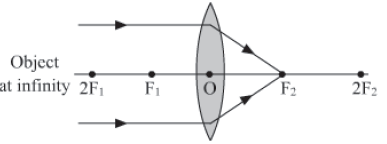
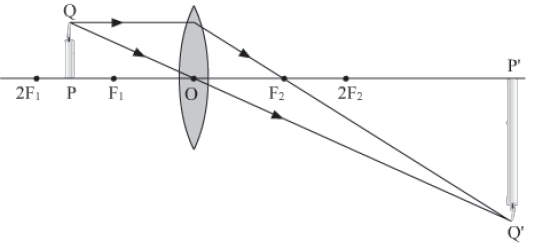
II. When the object is beyond the centre of 2F1.

III. When the object is at the centre of curvature 2F1.

IV. When the object is placed between the focus F1 and 2F1.
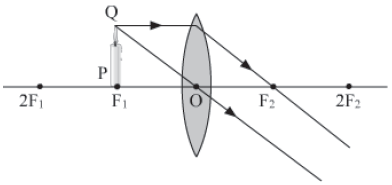
V. When the object is placed at focus F1.
VI. When the object is placed between the focus F1 and optical centre O.

The position, size, and nature of the image formed by a convex lens can be summarized in the table below.


Different Types of Electromagnetic Waves

Uses of Electromagnetic radiations:
Light: It has very important role in our life. Human eye is sensitive to only this visible part of electromagnetic radiations. Anything which we able to see is because of the light.
(i) Gamma rays: These were first discovered radioactive emitted radiation. They are also present in cosmic radiations. Gamma rays have extensive applications,
* Most energetic electromagnetic radiations of wavelength less than 0.01 nm.
* These are used in the treatment of cancer.
* Used in γ-ray microscope.
* Acts as catalyst in the manufacturing of some chemicals.
* These are used to produce photoelectric effect.
* These rays are also used in radiography.
(ii) X-rays: William Rontgen was awarded Nobel prize in 1901 for his discovery of Xrays. X-rays are used in,
* Wavelength range between 0.01 nm to 10 nm.
* Fractured bones are located by the X-rays.
* X-rays are used in the treatment of cancer and skin diseases.
* These rays used to locate foreign bodies such as bullets, coins, pins etc in human body.
* X-rays are used in radiography.
* They are also used in the study of crystal structure.
(iii) Ultraviolet radiations: These rays were detected by J.W. Ritter in 1801. These are harmful to living tissues and are absorbed by the ozone layer present in our atmosphere. Its applications are,
* Wavelength range between 10 nm to 400 nm.
* UV rays are used as efficient sterilizers.
* UV rays are used to activate some chemical reactions.
* These are used in fluorescent lamps.
* UV rays used in identifying real gems and artificial gems.
* They are used in the treatment of skin diseases, diseases of the bone and rickets.
* They are used in synthesizing vitamin-D in our body.
* They are also used in the operation of photoelectric alarms.
(iv) Visible light: The electromagnetic radiations of wavelength from 400 nm to 800 nm are known as visible light. This part of the spectrum has been discovered by Newton by passing sunlight through a prism. Its applications are
* In photography
* In photosynthesis
* In enabling us to see objects around us
(v) Infrared radiations: It has heating effect which was first detected by W. Herschel in 1800. Its applications are,
* Wavelength range between 800 nm to 1 mm.
* Infrared spectrum is used to identify and determine molecular structure of a compound.
* Found suitable for long distance photography.
* Infrared photography is used to determine enemy movement during war, examine and detect forgery in old paintings
* These rays has a role in medical field, these are useful in the diagnosis of superficial tumours, dislocation of bones and in the treatment of sprains.
* It stimulates blood circulation.
* TV remote also uses infrared rays to control different settings.
* Infrared radiations from sun are used in the working of solar energy devices.
(vi) Microwaves: These are vastly used for experimental purposes. Also find applications in Radar, Satellite communication and microwave ovens.
* Wavelength range between 1 mm to 10 m.
* Found suitable for long distance photography.
* Infrared photography is used to determine enemy movement during war, examine and detect forgery in old paintings.
* These rays have role in medical field. These are useful in the diagnosis of superficial tumors, dislocation of bones and in the treatment of sprains.
* It stimulates blood circulation.
(vii) Radio waves: As there name suggest, these waves are used in radio and television.
* Wavelength range above 10 m.
* Short wavelength radio waves are used in communication systems including satellite systems, Radars and TV broadcasting.
* Longer wavelength radio waves are used in radio broadcasting.







