Students can refer to the following Sample Paper ICSE Class 10 Mathematics Set G with Answers provided below based on the latest syllabus and examination guidelines issued for ICSE Mathematics. All specimen papers have been prepared covering all chapters given in ICSE Mathematics book for Class 10. You should also refer to ICSE Class 10 Mathematics Solutions.
Sample Paper ICSE Class 10 Mathematics Set G with Answers
Subject: Mathematics
Answer to this paper must be written on the paper provided separately.
You will not be allowed to write during the first 15 minutes.
This time is to be spent in reading the question paper.
The time given at the head of this Paper is the time allowed for writing the answers.
Attempt all questions from Section A and any four questions from Section B.
• All working including rough work must be clearly shown and must be done on the same sheet as
the rest of the answers.
• Omission of essential working will result in loss of marks.
The intended marks for the questions or parts of questions are given in brackets ( ).
Mathematical tables are provided.
Sample Paper ICSE Class 10 Mathematics Set G
SECTION A [40 MARKS]
Attempt all questions in this section.
•Question 1
a) Find the value ‘K’ if 4x3 – 2x2 + kx + 5 leaves remainder -10 when divided by 2x + 1. (3)
b) Amit deposits 1600 per month in a bank for 18 months in a recurring deposit account. If he gets 31080 at the time of maturity, what is the rate of interest per annum? (3)
c) Use ruler and compasses for this question: (4)
i. Draw a circle with centre O and radius 4cm.
ii. Mark a point P such that OP = 7cm. Construct the two tangents to the circle from P. Measure and record the length of one of the tangents.
Question 2
a) Solve the following inequations and represent your solution on the real number line. -(3)

b) Find the 16th term of the A.P. 7, 11, 15, 19 …….. find the sum of the first 6 terms.
c) In the given figure, CE is a tangent to the circle at point C. ABCD is a cyclic quadrilateral. If ∠ABC = 930 and ∠DCE = 350 find:
i. ∠ADC
ii. ∠CAD
iii. ∠ACD

Question 3
a) Prove the following identity:

b) Find x and y if:

c) For what value of ‘K’ will be following quadratic equations: (4)
(K + 1) x2 – 4Kx + 9 = 0 have real and equal roots? Solve the equations.
Question 4
a) A box consists of 4 red, 5 black and 6 white balls. One ball is drawn out at random. Find the probability that the ball drawn is (3)
i. Black
ii. Red or white
b) Calculate the median and mode for the following distribution.

c) A container shaped like a right circular cylinder having diameter 12cm and height 15cm is full of ice-cream. The ice-cream is to be filled into comes of height 12cm and diameter 6cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
SECTION B [40 MARKS]
Answer any 4 questions from this section.
Question 5
a) The 2nd and 45th term of an arithmetic progression are 10 and 96 respectively. Find the first term and the common difference and hence find the sum of the first 15 terms.(3)
b) If A = ,

find matrix B such that A2 – 2B = 3A + 5I where I is a 2 x 2 identify matrix.(3)
c) With the help of a graph paper, taking 1cm = 1 unit along both x and y axis. (4)
i. Plot points A (0,3), B (3,0), D (2, -3), E (0, -3), C (3, 0)
ii. Reflect points B, C and D on the y axis and name them as B’, C’ and D’ respectively.
iii. Write the co-ordinates of B’, C’ and D’.
iv. Write the equations of line B’ D’.
v. Name the figure BCDD’C’B’B.
Question 6
a) In ∠ABC and ∠EDC, AB is parallel to ED. (3)
BD = 1/2 BC and AB = 12.3 cm.
i. Prove that ∠ABC ≅ ∠EDC
ii. Find DE
iii. Find:


b) Find the ratio in which the line joining (-2, 5) and (-5, -6) is divided by the line y=-3. Hence, Find the point of intersection.(3)
c) The given solid figure is a cylinder surmounted by a cone. The diameter of the base of the cylinder is 6cm. The height of the cone is 4cm and the total height of the solid is 25cm. Take π = 22/7 , find the:
i. Volume of the solid
ii. Curved surface area of the solid.

Question 7
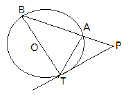
a) In the given figure, PAB is a secant and PT a tangent to the circle with centre O.
If ∠ATP = 400, PA = 9cm and AB = 7cm
Find:
i. ∠APT
ii. Length of PT
b) The 1st and the 8th term of a GP are 4 and 512 respectively. Find (3)
i. The common ratio
ii. The sum of its first 5 terms
c) Calculate the mean of the following distribution using step-deviation method.

Question 8
a) Prove the following identity: (3)
(sinA + cosecA)2 + (cosA + secA)2 = 5 + sec2A.cosec2A
b) Find the equation of the perpendicular bisector of line segment joining A(4, 2) and B(-3, -5).(3)
c) Using properties of proportion, find x: y if
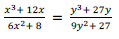
Question 9
a) The difference of the squares of two natural numbers is 84. The square of the larger number is 25 times the smaller number. Find the numbers. (4)
b) The following table shows the distribution of marks in Mathematics. (6)

With help of a graph, taking 2cm = 10 units along one axis and 2cm = 10 units
along the other axis, plot an ogive for the above distribution and use it to find the:
i. Median
ii. Number of students who scored distinction marks (75%) and above.
iii. Number of students, who passed the examination if pass marks is 35%.
Question 10
a) Prove that two tangents drawn from an external point to a circle are of equal length.
b) i. A(-1, 3), B(4, 2) and C(3, -2) are the vertices of a triangle. (3)
ii. Find the coordinate of the centroid of the triangle.
iii. Find the equation of the line through G and parallel to AC.
c) A man bought 200 shares each of face value 10 at 12 per share. At the end of the year, the company from which he bought the shares declares a dividend of 15%, calculate:
i. The amount of money invested by the man.
ii. The amount of dividend he received.
iii. The percentage return on his outlay.
Question 11
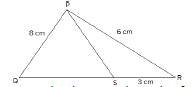
a) PQR is a triangle.
S is a point on the side QR of ∠PQR such that ∠PSR= ∠QPR (3)
Given QP = 8cm, PR = 6cm and SR = 3cm
i. Prove ∠PQR ∼ ∠SPR
ii. Find the length of QR and PS.

b) Two poles AB and PQ are standing opposite each other on either side of a road 200m wide. From a point R between them on the road, the angles of elevation of the top of the poles AB and PQ are 450 and 400 respectively. If height of AB=80cm, find the height of PQ correct to the nearest metre. (3)
c) Construct a triangle PQR, gives RQ = 10cm, ∠PRQ = 750 and base RP = 8cm.(4)
Find by construction.
i. The locus of points which are equidistant from QR and QP.
ii. The locus of points which are equidistant from P and Q.
iii. Mark the point O which satisfies conditions (i) and (ii).