Question 1. In the figure, given below, straight lines AB and CD intersect at P; and AC||BD. Prove that:
(i) ∆APC and ∆BPD are similar.
(ii) If BD = 2.4 cm AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm; find the lengths of PA and PC.

Solution:
(i) In given triangle ∆APC and ∆BPD
∠APC = ∠BPD (Vertically opposite angles)
∠ACP = ∠BDP (Vertically opposite angles)
∆APC ~ ∆BPD (by AA criterion)
Hence, ∆APC and ∆BPD are similar
(ii) Given that, BD = 2.4 cm AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm
As proved above ∆APC ~ ∆BPD

Question 2. In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that:
(i) ∆APB is similar to ∆CPD
(ii) PA × PD = PB × PC
Solution:
(i)
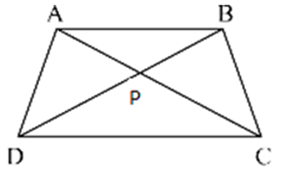
In ∆APB and ∆CPD
∠APB = ∠CPD (Vertically opposite angles)
∠ABP = ∠CDP (Vertically opposite angles)
∆APB ~ ∆CPD (by AA criterion)
(ii)

In ∆APB and ∆CPD
∠APB =∠CPD (Vertically opposite angles)
∠ABP =∠CDP (Vertically opposite angles)
∆APB ~ ∆CPD (by AA criterion)
PA/PC = PB/PD (By corresponding sides of similar triangles are equal)
By cross-multiplication,
PA × PD = PB × PC
Question 3. P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that:
(i) DP: PL = DC: BL.
(ii) DL: DP = AL: DC.
Solution:
(i)
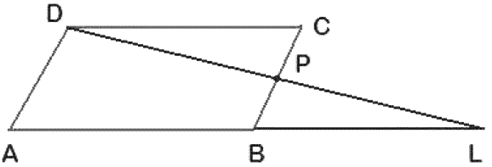
It is given that, P is a point on side BC of a parallelogram ABCD.
AD||BC, that is AD||BP,
By Basic Proportionate theorem,

(ii)

It is given that, P is a point on side BC of a parallelogram ABCD.
AD || BC, that is AD || BP,
By Basic Proportionate theorem,

Question 4. In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO=2DO; show that:
(i) ∆AOB is similar to ∆COD.
(ii) OA × OD – OB × OC.
Solution:

It is given that, AO = 2CO and BO=2DO
By Basic Proportionate theorem,
AO/CO = 2/1 = BO/DO
∠AOB=DOC (Vertically opposite angles)
∆AOB~∆DOC (SAS criterion)
(ii)

By Basic Proportionate theorem,
AO/CO = 2/1 = BO/DO
Hence, OA×OD = OB×OC
Question 5. In ∆ABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that:
(i) CB: BA = CP: PA
(ii) AB × BC = BP × CA
Solution:
(i)

It is given that, in ∆ABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P.
∠ABC = 2∠ACB
Let us assumed that, ∠ACB = x
∠ABC = 2∠ACB
∠ABC = 2x
It is given that, BP is the bisector of ∠ABC.
∠ABP = ∠PBC
∠ABP = ∠PBC = x
Using the angle bisector theorem, the bisector of an angle divides the side opposite to it in the ratio of other two sides.
Hence, CB : BA = CP : PA.
(ii)

In ΔABC and ΔAPB,
∠BCP = ∠ABP (given)
∠ABC = ∠APB (by exterior angle property)
∆ABC ~ ∆APB (by AA criterion)
Now, since corresponding sides of similar triangles are proportional we have
CA/AB = BC/BP
By cross-multiplication,
Hence, AB × BC = BP × CA
Question 6. In ∆ABC; BM ⏊ AC and CN ⏊ AB; show that:

Solution:

In ΔABM and ΔACN,
∠AMB = ∠ANC (BM ⏊ AC)
∠BAM = ∠CAN (common)
∆ABM ~ ∆ACN (by AA criterion)
Now, since corresponding sides of similar triangles are proportional we have

Question 7. In the given figure, DE||BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm.
(i) Write all possible pairs of similar triangles.
(ii) Find lengths of ME and DM.

Solution:
(i)
In ΔAME and ΔANC,
∠AME = ∠ANC (DE || BC)
∠MAE = ∠NAC (common)
∆AME~∆ANC (by AA criterion)
In ΔADM and ΔABN,
∠ADM = ∠ABN (DE || BC)
∠DAM = ∠BAN (common)
∆ADM ~ ∆ABN (by AA criterion)
In ΔADE and ΔABC,
∠ADE = ∠ABC (DE||BC)
∠AED = ∠ACB (common)
∆ADE ~ ∆ABC (by AA criterion)
(ii)
In ΔAME and ΔANC,
∠AME = ∠ANC (DE || BC)
∠MAE = ∠NAC (common)
∆AME ~ ∆ANC (by AA criterion)
Now, since corresponding sides of similar triangles are proportional we have

Question 8. In the given figure, AD =AE and AD2 = BD × EC Prove that: triangles ABD and CAE are similar.

Solution:
In ΔABD and ΔCAE,
∠ADM = ∠ABN (opposite angles on equal sides)
∠ADB = ∠AEC (∠ADB + ∠ADE = 180˚ and ∠AEC + ∠AED = 180˚)
Also,
AD2 = BD × EC
AD/BD = EC/AD
AD/BD = EC/AE
ΔABD ~ ΔCAE (by SAS criterion)
Question 9. In the given figure, AB || DC, BO = 6 cm and DQ = 8 cm; find: BP × DO.

Solution:
It is given that, AB || DC, BO = 6 cm and DQ = 8 cm.
∠QDO = ∠PBO (AB || DC and PB || DQ)
∠DOQ = ∠BOP (vertically opposite angle)
∆DOQ ~ ∆BOP (by AA criterion)
Now, since corresponding sides of similar triangles are proportional we have
DO/BO = DQ/BP
DO/6 = 8/BP
By cross-multiplication,
DO×BP = 6×8
DO×BP = 48 cm2
Question 10. Angle BAC of triangle ABC is obtuse and AB = AC. P is a point in BC such that PC = 12 cm. PQ and PR are perpendiculars to sides AB and AC respectively. If PQ = 15 cm and PR=9 cm; find the length of PB.
Solution:

It is given that, angle BAC of triangle ABC is obtuse and AB = AC
In ∆ABC,
AC = AB (given)
∠ABC = ∠ACB (angle opposite equal sides are equal)
In ∆PRC and ∆PQB,
∠ABC = ∠ACB (Proved above)
∠PRC = ∠PQB (each 90˚)
∆PRC ~ ∆PQB (by AA criterion)

Question 11. State, true or false:
(i) Two similar polygons are necessarily congruent.
(ii) Two congruent polygons are necessarily similar.
(iii) All equiangular triangles are similar.
(iv) All isosceles triangles are similar.
(v) Two isosceles-right triangles are similar.
(vi) Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
(vii) The diagonals of a trapezium, divide each other into proportional segments.
Solution:
(i) Two similar polygons are necessarily congruent. False
(ii) Two congruent polygons are necessarily similar. True
(iii) All equiangular triangles are similar. True
(iv) All isosceles triangles are similar. False
(v) Two isosceles-right triangles are similar. True
(vi) Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other. True
(vii) The diagonals of a trapezium, divide each other into proportional segments. True
(i) Two similar polygons are necessarily congruent. False
Question 12. Given ∠GHE = ∠DFE = 90°, DH=8,DF = 12, DG = 3x – 1 and DE = 4x + 2. Find; the lengths of segments DG and DE.

Solution:
It is given that, ∠GHE = ∠DFE = 90°, DH = 8,DF = 12, DG = 3x-1 and DE = 4x + 2
In ∆DHG and ∆DFE,
∠GDH = ∠FDE (common)
∠GHD = ∠DFE (each 90˚)
∆DHG ~ ∆DFE (by AA criterion)

By cross-multiplication,
8(4x + 2) = 12(3x – 1)
32x + 16 = 36x – 12
32x – 36x = -12-16
-4x = -28
x = (-28)/(-4)
x = 7
DG = 3x – 1
DG = 3(7) – 1
DG = 21 – 1
DG = 20
DE = 4x + 2
DE = 4(7) + 2
DE = 28 + 2
DE = 30
Hence, the value of DG and DE is 20 and 30 respectively.
Question 13. D is a point on the side BC of triangle ABC such that angle ADC is equal to angle BAC. Prove that CA2 = CB × CD.
Solution:

In Δ𝐴𝐷𝐶 and Δ𝐵𝐴𝐶
∠𝐴𝐷𝐶 = ∠𝐵𝐴𝐶 (given)
∠𝐴𝐶𝐷 = ∠𝐴𝐶𝐵 (common)
Δ𝐴DC ~ ΔBAC (by AA criterion)
𝐶𝐴𝐶𝐵 = 𝐶𝐷𝐶𝐴
By cross-multiplication,
𝐶𝐴 × 𝐶𝐴 = 𝐶𝐷 × 𝐶𝐵
𝐶𝐴2 = 𝐶𝐷 × 𝐶𝐵
Hence proved.
Question 14. In the given figure, ΔABC and ΔAMP are right angled at B and M respectively. Given AC = 10 cm, AP = 15 cm and PM = 12 cm.
(i) Prove that ΔABC ~ ΔAMP
(ii) Find AB and BC.
Solution:
(i) In Δ𝐴𝐵𝐶 and Δ𝐴𝑀𝑃
∠𝐵𝐴𝐶 = ∠𝑃𝐴𝑀 (Common)
∠𝐴𝐵𝐶 = ∠𝑃𝑀𝐴 (each 90˚)
Δ𝐴BC ~ ΔAMP (by AA criterion)

Question 15. Given : RS and PT are altitudes of A PQR prove that:
(i) ∆PQT ~ ∆QRS,
(ii) PQ × QS = RQ × QT.
Solution:
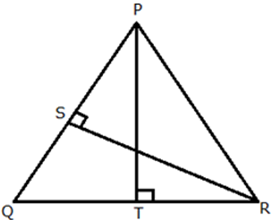
(i) In ∆PQT and ∆QRS
∠PTQ = ∠RSQ (each 90˚)
∠PQT = ∠RQS (common)
∆PQT ~ ∆RQS (by AA criterion)
(ii) ∆PQT ~ ∆RQS (proved above)
PQ/RQ = QT/QS
By cross-multiplication,
PQ/RQ = QT/QS
PQ×QS = QT × RQ
Question 16. ABCD is a rhombus, DPR and CBR are straight lines Prove that: DP × CR = DC × PR.

Solution:
In ∆DPA and ∆RPC
∠DPA = ∠RPC (Vertically opposite angles)
∠PAD = ∠PCR (alternate interior angle)
∆DPA~∆RPC
DP/PR = AD/CR
By cross-multiplication,
DP×CR = AD×PR
Hence proved.
Question 17. Given: FB = FD, AE ⏊ FD and FC ⏊ AD. Prove:

Solution:
It is given that, 𝐹𝐵 = 𝐹𝐷, AE ⏊ FD and FC ⏊ AD
∠𝐹𝐷𝐵 = ∠𝐹𝐵𝐷
In Δ𝐴𝐸𝐷 = Δ𝐹𝐶𝐵
∠𝐴𝐸𝐷 = ∠𝐹𝐶𝐵 (each 90˚)
∠𝐴𝐷𝐸 = ∠𝐹𝐵𝐶 (from equation 1)
Δ𝐴𝐸𝐷 ~ Δ𝐹𝐶𝐵 (by AA criterion)
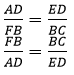
Question 18. In Δ PQR, ∠ Q = 90° and QM is perpendicular to PR, Prove that:
(i) PQ2 = PM×PR
(ii) QR2 = PR×MR
(iii) PQ2 + QR2 = PR2
Solution:

(i) In ∆PQM and ∆PQR
∠PMQ = ∠PQR (each 90˚)
∠QPM = ∠RPQ (common)
∆PQM ~ ∆PRQ (by AA criterion)
𝑃𝑄/𝑃𝑅 = 𝑃𝑀/𝑃𝑄
By cross – multiplication,
𝑃𝑄×𝑃𝑄 = 𝑃𝑀×𝑃𝑅
𝑃𝑄2 = 𝑃𝑀×𝑃𝑅
(ii) In Δ𝑄𝑀𝑅 and Δ𝑃𝑄𝑅
∠𝑄𝑀𝑅 = ∠𝑃𝑄𝑅 (each 90˚)
∠𝑄𝑅𝑀 = ∠𝑄𝑅𝑃 (common)
Δ𝑄𝑀𝑅 ~ Δ𝑃𝑄𝑅 (by AA criterion)
𝑄𝑅/𝑃𝑅 = 𝑀𝑅/𝑄𝑅
By cross – multiplication,
𝑄𝑅×𝑄𝑅 = 𝑀𝑅×𝑃𝑅
𝑄𝑅2 = 𝑀𝑅×𝑃𝑅
(iii) By Adding both the equations,
𝑃𝑄2 + 𝑄𝑅2 = (𝑃𝑀×𝑃𝑅) + (𝑀𝑅×𝑃𝑅)
𝑃𝑄2 + 𝑄𝑅2 = 𝑃𝑀×𝑃𝑅 + 𝑀𝑅×𝑃𝑅
𝑃𝑄2 + 𝑄𝑅2 = 𝑃𝑅(𝑃𝑀 + 𝑀𝑅)
𝑃𝑄2 + 𝑄𝑅2 = 𝑃𝑅(𝑃𝑅)
𝑃𝑄2 + 𝑄𝑅2 = 𝑃𝑅2
Hence proved.
Question 19. In ΔABC, ∠ B = 90° and BD × AC.
(i) If CD = 10 cm and BD = 8 cm; find AD.
(ii) If AC = 18 cm and AD = 6 cm; find BD.
(iii) If AC = 9 cm, AB = 7 cm; find AD.
Solution:

(i) In ∆CDB,
∠1 + ∠2 + ∠3 = 180˚
Given that, the value of angle 2 is 90˚
∠1 + 90˚ + ∠3 = 180˚
∠1 + ∠3 = 180˚-90˚
∠1 + ∠3 = 90˚_________(i)
∠3 + ∠4 = 90˚ _________(ii)
From (i) and (ii)
∠1 + ∠3 = ∠3 + ∠4
∠1 = ∠4
Also,
∠2 = ∠5 = 90˚
∆CDB~∆BDA (by AA criterion)
CD/BD = BD/AD
By cross-multiplication,
CD × AD = BD×BD
BD2 = CD×AD
(8)2 = 10×AD
64 = 10×AD
AD = 64/10
AD = 6.4
(ii) We have,
BD/DA = CD/BD
By cross-multiplication,
BD × BD = CD×DA
BD2 = 6×(18-6)
BD2 = 6×12
BD2 = 72
BD = √72
BD = 8.5cm
(iii) We know that,
∆ADB ~ ∆ABC

Question 20. In the figure, PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm. L is a point on PR such that RL : LP = 2:3. QL produced meets RS at M and PS produced at N. Find the lengths of PN and RM.

Solution:
In ∆RLQ and ∆PLN
∠RLQ = ∠PLN (Vertically opposite angle)
∠LRQ = ∠LPN (Alternate interior angle)
∆RLQ ~ ∆PLN (by AA criterion)

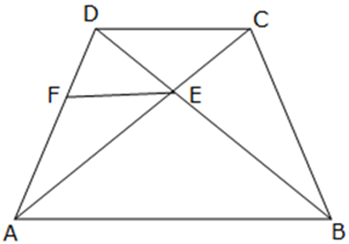
Question 21. In quadrilateral ABCD, diagonals AC and BD intersect at point E. Such that AE:EC = BE : ED. Show that ABCD is a parallelogram.
Solution:
Given:- AE : EC = BE : ED
Construction:- Draw EF || AB

Question 22. In ∆ ABC, AD is perpendicular to side BC and AD2 = BD × DC. Show that angle BAC = 90°

Solution:
It is given that, AD2 = BD × DC
AD/DC = BD/AD
∠ADB = ∠ADC (each 90˚)
∆DBA~∆DAC (by SAS criterion)
Two triangles will be equiangular
∠1 = ∠C and ∠2 = ∠B
∠1 + ∠2 = ∠B + ∠C
∠A = ∠B + ∠C
By angle sum property we know that,
∠A + ∠B + ∠C = 180˚
∠A + ∠A = 180˚
2∠A = 180˚
∠A = 180˚/2
∠A = ∠BAC = 90˚
Question 23. In the given figure AB||EF||DC; AB ~ 67.5 cm. DC = 40.5 cm and AE = 52.5 cm.
(i) Name the three pairs of similar triangles.
(ii) Find the lengths of EC and EF.

Solution:
(i) The three pair of similar triangles are:
∆BEF and ∆BDC
∆CEF and ∆CAB
∆ABE and ∆CDE
(ii) Since, ∆ABE and ∆CDE are similar,

Question 24. In the given figure, QR is parallel to AB and DR is parallel to QB. Prove that — PQ2 = PD × PA.

Solution:
It is given that, QR is parallel to AB and DR is parallel to QB.

Question 25. Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that : EL = 2 BL.
Solution:

It is given that, through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E.
∠1 = ∠6 (alternate interior angle)
∠2 = ∠3 (alternate interior angle)
DM = MC (M is the mid-point)
∆ABE ≅ ∆CDE (by ASA congruence criterion)
DE = BC (by CPCT)
AD = BC (opposite sides of a parallelogram)
AE = AD + DE
AE = AD + DE
AE = 2BC
Now,
∠1 = ∠6 (alternate interior angle)
∠4 = ∠5 (alternate interior angle)
∆ELA ~ ∆BLC (by AA criterion)

Exercise 15B
Question 1. In the following figure, point D divides AB in the ratio 3:5. Find:
(i) AE/EC (ii) AD/AB (iii) AE/AC Also, if:
(iv) DE = 2.4 cm, find the length of BC. (v) BC = 4.8 cm, find the length of DE.

Solution:



Question 2. In the given figure, PQ || AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find:
(i) CP/PA
(ii) PQ
(iii) If AP = x, then the value of AC in terms of x.

Solution:
(i) In ∆CPQ and ∆CAB
∠PCQ = ∠ACB (DE || BC corresponding angles)
∠C = ∠C (common)
∆CPQ ~ ∆CAB (by AA criterion)

Question 3. A line PQ is drawn parallel tp the side BC of AABC which cuts side AB at P and side AC at Q. If AB = 9.0 cm, CA=6.0 cm and AQ = 4.2 cm, find the length of AP.
Solution:

In ∆APQ and ∆ABC
∠ACQ =∠ABC (PQ || BC corresponding angles)
∠PAQ =∠BAC (common)
∆APQ ~ ∆ABC (by AA criterion)

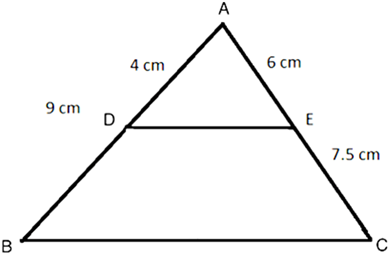
Question 4. In ∆ABC, D and E are the points on sides AB and AC respectively. Find whether DE||BC, if:
(i) AB=9 cm, AD=4 cm, AE=6 cm and EC = 7.5 cm.
(ii) AB=63 cm, EC=11.0 cm, AD=0.8 cm and AE = 1.6 cm.
Solution:
(i)

(ii)


Question 5. In the given figure, ∆ABC ~ ∆ADE. If AE: EC = 4 :7 and DE = 6.6 cm, find BC. If ‘x’ be the length of the perpendicular from A to DE, find the length of perpendicular from A to DE find the length of perpendicular from A to BC in terms of ‘x’.
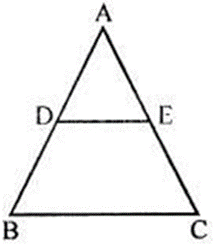
Solution:

It is given that, ∆ABC~∆ADE
∠ABC = ∠ADE and ∠ACB = ∠AED
So, DE || BC
Also,
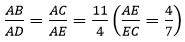
In ∆ADP and ∆ABQ
∠ADP = ∠ABQ (DP || BQ corresponding angles)
∠APD = ∠AQB (DP || BQ corresponding angles)
∆ADP ~ ∆ABQ (by AA criterion)

Question 6. A line segment DE is drawn parallel to base BC of ∆ABC which cuts AB at point D and AC at point E. If AB = 5 BD and EC=3.2 cm, find the length of AE.
Solution:
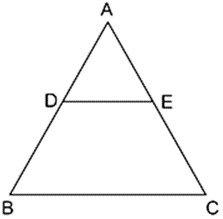
It is given that, A line segment DE is drawn parallel to base BC of ∆ABC which cuts AB at point D and AC at point E.
DE || BC, ∆ADE ~ ∆ABC

Question 7. In the figure, given below, AB, Cd and EF are parallel lines. Given AB = 7.5 cm, DC =y cm, EF=4.5 cm, BC=x cm and CE=3 cm, calculate the values of x and y.

Solution:

By cross – multiplication,
(3x + 9)7.5 = 4.5x(x + 3)
22.5x + 67.5 = 4.5x2 + 13.5x
4.5x2 + 13.5x – 22.5x – 67.5 = 0
4.5x2 – 9x – 67.5 = 0
4.5(x2 – 2x – 15) = 0
x2 – 2x – 15 = 0
x2 – 5x + 3x – 15 = 0
x(x – 5) + 3(x – 5) = 0
(x + 3)(x – 5) = 0
x + 3 = 0 x – 5 = 0
x = – 3 x = 5
Side of a triangle is 5 cm.
Put the value of x in equation (ii)
y = 4.5(5)/5 + 3
y = 2.8125
Hence, the value of x is 5 and y = 2.8125.
Question 8. In the figure, given below, PQR is a right – angle triangle right angled at Q. XY is parallel to QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1:2. Calculate the lengths of PR and QR.

Solution:

𝑅 = 8
Here, PR = PY + YR
PR = 4cm + 8cm
PR = 12cm
Δ𝑃𝑄𝑅 is a right-angled triangle
𝑄𝑅 2 = 𝑃𝑅2 − 𝑃𝑄2 (By Pythagoras theorem)
𝑄𝑅2 = (12)2 − (6)2
𝑄𝑅2 = 144 − 36
𝑄𝑅2 = 108
𝑄𝑅 = √108
𝑄𝑅 = 10.39cm
Question 9. In the following figure, M is mid-point of BC of a parallelogram ABCD. DM intersects the diagonal AC at P and AB produced at E. Prove that PE = 2PD.
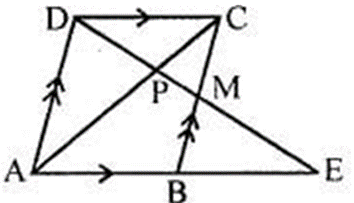
Solution:
In ∆BME and ∆DMC
∠BME = ∠CMD (Vertically opposite angles)
∠MCD = ∠MBE (Alternate interior angles)
BM = BC (M is the mid-point)
∆BME≅∆DMC (by AA criterion)
BE = DC = AB
In ∆DCP and ∆EPA
∠DPC = ∠EPA (Vertically opposite angles)
∠CDP = ∠AEP (Alternate interior angles)
∆DCP ~ ∆EAP (by AA criterion)

Question 10. The given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm. find the perimeter of the parallelogram ABCD.

Solution:
It is given that, E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm.
In ∆DEC and ∆EAF
∠DEC = ∠EAF (Vertically opposite angles)
∠EDC = ∠EAF (Alternate interior angles)
∆DEC ≅ ∆AEF (by AA criterion)

Perimeter of the parallelogram ABCD = AB + BC + CD + AD
=12 + 10 + 12 + 10
=44cm
Hence, the Perimeter of the parallelogram ABCD is 44cm.
Exercise 15C
Question 1. (i) The ratio between the corresponding sides of two similar triangles is 2 is to 5. Find the ratio between the areas of these triangles.
(ii) Areas of two similar triangles are 98 sq. cm and 128 sq. cm. Find the ratio between the lengths of their corresponding sides.
Solution:
We know that the ratio of two identical triangles’ areas is equal to the ratio of their corresponding sides’ squares.

Question 2. A line PQ is drawn parallel to the base BC, of ∆ ABC which meets sides AB and AC at points P and Q respectively. If AP = 1/3 PB; find the value of:


Solution:
(i) Given that AP = 1/3 PB
AP/PB = 1/3
In ∆APQ and ∆ABC,
∠APQ = ∠ABC (PQ||BC, corresponding angles are equal)
∠AQP = ∠ACB
∠APQ ~ ∠ABC

Question 3. The perimeters of two similar triangles are 30 cm and 24cm. If one side of first triangle is 12cm, determine the corresponding side of the second triangle.
Solution:
Let us assumed that, ∠ABC ~ ∠DEF

Question 4. In the given figure AX : XB = 3 : 5.
Find:
(i) The length of BC, if length of XY is 18 cm.
(ii) Ratio between the areas of trapezium XBCY and triangle ABC.

Solution:


Question 5. ABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such that PQ || BC and divides triangle ABC into two parts equal in area. Find the value of ratio BP:AB. Given-In ∆ ABC, PQ||BC in such away that area APQ = area PQCB To Find— The ratio of BP : AB.

Solution:
It is given that, ar(∆APQ) = 1/2 ar(∆ABC)
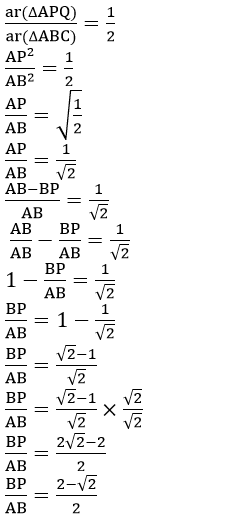
Question 6. In the given triangle PQR, LM is parallel to QR and PM : MR = 3 : 4.
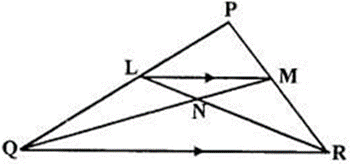
Calculate the value of ratio:

Solution:


Question 7. The given diagram shows two isosceles triangles which are similar also. In (he given diagram, PQ and BC are not parallel: PC = 4, AQ = 3, QB = 12, BC = 15 and AP = PQ.
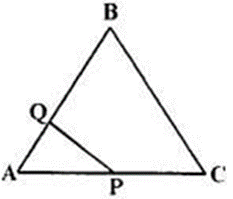
Calculate—
(i) the length of AP
(ii) the ratio of the areas of triangle APQ and triangle ABC.
Solution:
(i) It is given that, ∆AQP and ∆ACB

By cross-multiplication,
3 × 15 = 𝐴𝑃(4 + 𝐴𝑃)
45 = 4𝐴𝑃 + (𝐴𝑃)2
4𝐴𝑃 + 𝐴𝑃2 − 45 = 0
𝐴𝑃2 + 4𝐴𝑃 − 45 = 0
𝐴𝑃2 + 9𝐴𝑃 − 5𝐴𝑃 − 45 = 0
𝐴𝑃(𝐴𝑃 + 9) − 5(𝐴𝑃 + 9) = 0
(𝐴𝑃−5)(𝐴𝑃+9)=0
𝐴𝑃 − 5 = 0
𝐴𝑃 = 5
𝐴𝑃 + 9 = 0
𝐴𝑃 = −9
Hence, the value of AP is 5 unit.

Question 8. In the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP:PC=1:2. DP produced meets AB produced at Q. Given the area of triangle CPQ = 20cm2.
Calculate—
(i) area of triangle CDP
(ii) area of parallelogram ABCD

Solution:
(i) In ∆BPQ and ∆CPD,
∠BPQ = ∠CPD (Vertically opposite angles)
∠BQP = ∠PDC (Alternate angles)
∆BPQ ~ ∆CPD (By AA similarity)

By cross – multiplication,
Area of ∆CPD = 40 cm2
(ii) In ∆BQP and ∆AQD,
∠QBP = ∠QAD (BP || AD corresponding angles are equal)
∠BQP = ∠PDC (Common)
∆BQP ~ ∆AQD (By AA similarity)
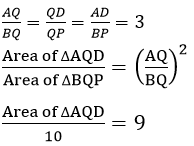
Area of ∆AQD = 90〖cm〗^2
Area of ADPB = Area of ∆AQD-Area of ∆AQD
Area of ADPB = 90cm2 – 10cm2
Area of ADPB = 80cm2
Area of ABCD=Area of ∆CDP + Area of ADPB
Area of ABCD = 40cm2 + 80cm2
Area of ADPB = 120cm2
Question 9. In the given figure. BC is parallel to DE. Area of triangle ABC = 25cm2. Area of trapezium BCED = 24 cm2 and DE = 14 cm. Calculate the length of BC. Also, Find the area of triangle BCD.
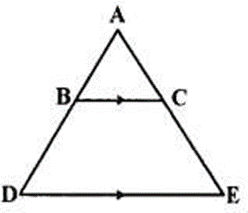
Solution:
In ∆ABC and ∆ADE,
∠ABC = ADE (BC || DE corresponding angles are equal)
∠ACB = ∠AED
∆ABC ~ ∆ADE (By AA similarity)

Question 10. The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3 : 5.

Find:
(i) ∆APB : ∆CPB
(ii) ∆DPC : ∆APB
(iii) ∆ADP : ∆APB
(iv) ∆APB : ∆ADB
Solution:
(i) In ∆APB and ∆CPB have common vertex at B and their bases AP and PC are along the same straight line.


Question 11. In the given figure, ARC is a triangle. DE is parallel to BC and AD/DB = 3/2 .
(i) Determine the ratios AD/DB = DE/BC.
(ii) Prove that ∆DEF is similar to ∆CBF. Hence, find EF/FB.
(iii) What is the ratio of the areas of ∆DEF and ∆BFC?
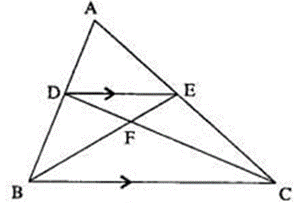
Solution:
(i)

It is given that, DE || BC and AD/DB = 3/2
In ∆ADE and ∆ABC,
∠A = ∠A (Corresponding angles)
∠ADE = ∠ABC (Corresponding angles)
∆ADE ~ ∆ABC (By AA similarity)

Question 12. In the given figure, ∠B = ∠E, ∠ACD = ∠BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the ∆ABC and ∆DEC

Solution:
It is given that, ∠ACD = ∠BCE,
∠ACD + ∠BCD = ∠BCE + ∠BCD
∠ACB = ∠DCE
It is also given that, ∠B = ∠E
∆ABC ~ ∆DCE

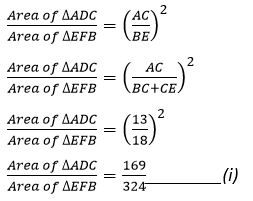
Question 13. Triangle ABC is an isosceles triangle in which AB = AC = 13 cm and BC = 10 cm. AD is perpendicular to BC. If CE = 8 cm and EF⏊ AB, find:


Solution:
(i) It is given that, AB = AC,
∠FBE + ∠ACD
∠BFE = ∠ADC
∆EFB ~ ∆ADC (By AA similarity)

Exercise 15D
Question 1. A triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A’ B’ C’. Calculate:
(i) the length of AB, if A’ B’ = 6 cm.
(ii) the length of C’ A’ if CA = 4 cm.
Solution:
(i) It is given that ∆ABC is enlarged by scale factor m=2.5 to the triangle A’B’C’.
A’B’=6cm
So,
AB(2.5 )= A’B’
AB(2.5) = 6
AB = 6/2.5
AB = 2.4 cm
(ii) It is given that ∆ABC is enlarged by scale factor m=2.5 to the triangle A’B’C’.
A’B’= 6cm
So,
AB(2.5) = A’B’
AB(2.5) = 6
AB = 6/2.5
AB= 2.4 cm
If CA=4cm
CA(2.5) = C’ A’
4(2.5) = C’ A’
10cm = C’ A’
C’ A’= 10cm
Question 2. A triangle LMN has been reduced by scale factor 0.8 to the triangle L’ M’ N’. Calculate:
(i) the length of M’ N’, if MN = 8 cm.
(ii) the length of LM, if L’ M’ = 5.4 cm.
Solution:
(i) It is given that, ∆LMN has been reduces by scale factor m=0.8 to the triangle L’M’N’.
MN=6cm
So,
MN(0.8) = M’N’
(8)(0.8) = M’N’
6.4cm = M’N’
M’N’= 6.4cm
(ii) It is given that, ∆LMN has been reduces by scale factor m=0.8 to the triangle L’M’N’.
L’M’=5.4cm
So,
LM(0.8 )= L’M’
LM(0.8) = 5.4cm
LM = 5.4/0.8 cm
LM = 6.75cm
Question 3. A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find:
(i) A’ B’, if AB = 4 cm.
(ii) BC, if B’ C’ = 15 cm.
(iii) OA, if OA’= 6 cm.
(iv) OC’, if OC = 21 cm. Also, state the value of:
(a) OB’/OB (b) C’ A’/CA
Solution:
(i) It is given that, ∆ABC is enlarged and the scale factor m = 3 to the ∆A’B’C’.
AB = 4cm
So,
AB(3) = A’B’
(4)(3) = A’B’
12cm = A’B’
A’B’ = 12cm
(ii) It is given that, ∆ABC is enlarged and the scale factor m = 3 to the ∆A’B’C’.
B’C’ = 15cm
So,
BC(3) = B’C’
BC(3) = 15
BC = 15/3
BC = 5cm
(iii) It is given that, ∆ABC is enlarged and the scale factor m = 3 to the ∆A’B’C’.
OA’ = 6cm
So,
OA(3) = OA’
OA(3) = 6
OA = 6/3
OA = 2cm
(iv) It is given that, ∆ABC is enlarged and the scale factor m = 3 to the ∆A’B’C’.
OC = 21cm
So,
OC(3) = OC’
21(3) = OC’
63cm = OC’
OC’= 63cm
The ratio of the lengths of two corresponding side s of two similar triangles.
(a) It is given that, ∆ABC is enlarged and the scale factor m = 3 to the ∆A’B’C’.
OB’/OB = 3
(b) It is given that, ∆ABC is enlarged and the scale factor m=3 to the ∆A’B’C’.
C’ A’/CA = 3
Question 4. A model of an aeroplane is made to a scale of 1:400. Calculate:
(i) the length, in cm, of the model; if the length of the aeroplane is 40 m.
(ii) the length, in m, of the aeroplane, if length of its model is 16 cm.
Solution:
(i) The ratio of the lengths of two corresponding sides to two similar triangles.
A model of an aeroplane is made to a scale of 1:400.
The length of the model = 1/400×4000
The length of the model = 10cm.
Hence, the length of the model is 10cm.
(ii) The ratio of the lengths of two corresponding sides of two similar tringles.
A model of an aeroplane is made to a scale of 1:400.
The length of the model = 16/100×400
The length of the model = 64cm.
Hence, the length of the model is 64cm.
Question 5. The dimensions of the model of a multistory building are 1.2 m × 75 cm × 2 m. If the scale factor is 1:30; find the actual dimensions of the building.
Solution:
The ratio of the lengths of two corresponding sides of two similar triangles.
The scale factor is 1:30.
The actual dimensions of the building = 30/1 (dimensions of the model of the building)

Question 6. On a map drawn to a scale of 1: 2,50,000; a triangular plot of land has the following measurements: AB = 3 cm, BC = 4 cm and angle ABC = 90°.
Calculate:
(i) the actual lengths of AB and BC in km.
(ii) the area of the plot in sq. km.
Solution:
(i) The ratio of the lengths if two corresponding sides of two similar triangles.
The scale factor is 1:2, 50,000

The actual length of AB = 3 × 2,50,000
The actual length of AB = 7,50,000
The actual length of AB = 7.5km

The actual length of BC = 4 × 2,50,000
The actual length of BC = 10,00,000
The actual length of BC = 10km
(ii) The area of the plot in sq. km

Question 7. A model of a ship of made to a scale 1 : 300
(i) The length of the model of ship is 2m. Calculate the lengths of the ship.
(ii) The area of the deck ship is 180,000m2. Calculate the area of the deck of the model.
(iii) The volume of the model in 6.5 m3. Calculate the volume of the ship.
Solution:
(i) It is given that, the Scale factor k = 1/300
Length of the model of the ship = k × Length of the ship

Question 8. An aeroplane is 30 in long and its model is 15cm long. If the total outer surface area of the model is 150cm2, find the cost of painting the outer surface of the aeroplane at the rate of Rs.120 per m2. Given that 50m2 of the surface of the aeroplane is left for windows.
Solution:
15cm represents = 30m
1cm represents = 3015
1cm represents = 2𝑚
1𝑐𝑚2 represents 2m × 2m = 4𝑚2
Surface area of the model = 150𝑐𝑚2
Actual surface area of aeroplane = 150×2𝑚×2𝑚
Actual surface area of aeroplane = 600𝑚2
50𝑚2 is left out for windows
Area to be painted = 600−50𝑚2
Area to be painted = 550𝑚2
Cost of painting per 𝑚2 = Rs. 120
Cost of painting per 550𝑚2 = Rs. 120 × 550𝑚2
Cost of painting per 550𝑚2 = Rs. 66000
Hence, the Cost of painting per 550𝑚2 = Rs. 66000



