Selina ICSE Class 10 Maths Solutions Chapter 17 Circles

Question 1. In the given figure, O is the centre of the circle. ∠OAB and ∠OCB are 30° and 40° respectively. Find ∠AOC. Show your steps of working.

Solution:

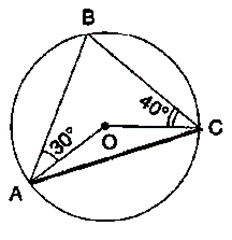
Given:- O is the centre of the circle. ∠OAB and ∠OCB are 30° and 40° respectively.
Construction:- Join AC
Let us assumed that, ∠OAC = ∠OCA = x
∠AOC = 180˚ – 2x
∠BAC = 30˚+x
∠BCA = 40˚+x
In ΔABC
∠ABC = 180˚ – ∠BAC – ∠BCA
∠ABC = 180˚-(30˚+x) – (40˚ + x)
∠ABC = 180˚ – 30˚ – x – 40˚ – x
∠ABC = 110˚ – 2x
∠AOC = 2∠ABC (Angle at the centre is double the angle at the circumference)
180˚ – 2x = 2(110˚ – 2x)
2x = 40˚
x = 20˚
∠AOC = 180˚ – 2×40˚
∠AOC = 140˚
Hence, the ∠AOC is 140˚

Question 2. In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
(i) Prove that AC is a diameter of the circle.
(ii) Find ∠ACB.

Solution
(i) Prove that AC is a diameter of the circle.
In ΔABD
∠DAB + ∠ABD + ∠ADB = 180˚
65˚ + 70˚ + ∠ADB = 180˚
∠ADB = 180˚-135˚
∠ADB = 45˚
∠ABC = ∠ADB + ∠BDC
∠ABC = 45˚ + 45˚
∠ABC = 90˚
Since, ∠ADC is the angle of semiarid,
Hence, AC is a diameter of the
(ii) We know that angles on the same segment of a circle are equal.
∠ACB = ∠ADB
∠ACB = 45˚

Question 3. Given O is the centre of the circle and ∠AOB = 70°. Calculate the value of:
(i) ∠OCA
(ii) ∠OAC

Solution:
We have, ∠AOB = 2ACB (angle at the centre is double the angle at the circumference subtended by the same chord)
∠ACB = 70˚/2
∠ACB = 35˚
OC = OA (Radius of same circle)
∠OCA = ∠OAC = 35˚

Question 4. In each of the following figures, O is the centre of the circle. Find the values of a, b, and c.
(i)

(ii)

Solution:
(i) We have b = 1/2 × 130˚ angle at the centre is double the angle at the circumference subtended by the same chord)
b = 65˚
Now, a +b = 180˚(Opposite angles of a cyclic quadrilateral are supplementary)
a + 65˚ = 180˚
a = 180˚ – 65˚
a = 115˚
(ii) We have c = 1/2 × Reflex( 112˚) (angle at the centre is double the angle at the circumference subtended by the same chord)

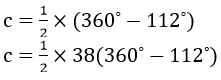
Question 5. In each of the following figures, O is the centre of the circle. Find the value of a, b, c and d.

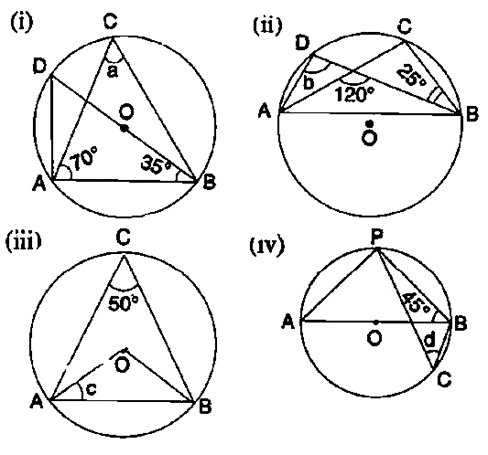
Solution:
(i) ∠BAD = 90˚ (Angle in a semicircle)
∠BDA = 90˚ – 35˚
∠BDA = 55˚ (Angle subtended by the same chord on the circle are equal)
(ii) ∠DAC = ∠CBD = 25˚ (Angle subtended by the same chord on the circle are equal)
120˚ = b + 25˚
-b = 25˚-120˚
b = 95˚ (In a triangle measure of exterior angle is equal to the sum of pair of opposite interior angles)(iii) ∠AOB = 2∠AOB
∠AOB = 2×50˚
∠AOB = 100˚ (angle at the centre is double the angle at the circumference subtended by the same chord)
OA = OB
∠OBA = ∠OAB = c
c = (80˚-100˚/2
c = 80˚/2
c = 40˚
(iv) ∠AOB = 90˚ (angle in a semicircle)
∠BAP = 90˚-45˚
∠BAP = 45˚
d = ∠BCP = ∠BAP = 45˚ (Angle subtended by the same chord on the circle are equal).

Question 6. In the figure, AB is common chord of the two circles. If AC and AD are diameters; prove that D, B and C are in a straight line. O₁ and O₂ are the centers of two circles.

Solution:
∠DBA = 90˚ and ∠CBA = 90˚ (angle in a semicircle is a right angle)
∠DBC = 180˚
D, B and C form a straight line.

Question 7. In the figure given below, find:
(i) ∠BCD
(ii) ∠ADC
(iii) ∠ABC

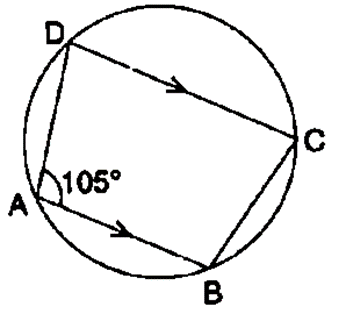
Show steps of your working.
Solution:
(i) ∠BCD + ∠BCD = 180˚ (Sum of opposite angle of a cyclic quadrilateral is 180˚)
∠BCD + 105˚ = 180˚
∠BCD = 180˚-105˚
∠BCD = 75˚
(ii) AB || CD
∠BAD + ∠ADC = 180˚ (Sum of opposite angle of a cyclic quadrilateral is 180˚)
105˚ + ∠ADC = 180˚
∠ADC = 180˚ – 105˚
∠ADC = 75˚
(iii) ∠ADC + ∠ABC = 180˚ (Sum of opposite angle of a cyclic quadrilateral is 180˚)
75˚ + ∠ABC = 180˚
∠ABC = 180˚ – 75˚
∠ADC = 105˚

Question 8. In the given figure, O is centre of the circle. If ∠ AOB = 140° and ∠ OAC = 50°, find :
(i) ∠ACB
(ii) ∠OBC
(iii) ∠OAB
(iv) ∠CBA

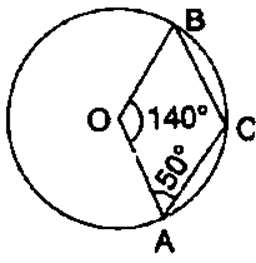
Solution:

∠ACB = 1/2 Reflex (∠AOB) (Angle at the centre is double the angle at the circumference subtended by the same chord)
∠ACB = 1/2(360˚ – 140˚)
∠ACB = 1/2(220˚)
∠ACB = 110˚
OA = OB (Radius of same circle)
∠OBA = ∠OAB
= 180˚-140˚/2
= 40˚/2
= 20˚
∠CAB = 50˚-20˚
∠CAB = 30˚
In ΔCAB,
∠CBA = 180˚ – 110˚-30˚
∠CBA = 40˚
∠OBC = ∠CBA+∠OBA
∠OBC = 40˚+20˚
∠OBC = 60˚

Question 9. Calculate:
(i) ∠CDB,
(ii) ∠ABC,
(ii) ∠ACB.

Solution:
It is given that,
∠CDB = ∠BAC = 49˚ (Angles subtended by the same chord on the circle are equal)
∠ABC = ∠ADC = 43˚ (Angles subtended by the same chord on the circle are equal)
By angle sum property we know that,
∠ACB = 180˚-49˚-43˚
∠ACB = 88˚
Hence, ∠ACB is 88˚.

Question 10. In the figure given below, ABCD is a cyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find:
(i) ∠BDC,
(ii) ∠BCD,
(iii) ∠BCA

Solution:
(i) By angle sum property of ΔABD,
∠ADB = 180˚ – 75˚ – 58˚
∠ADB = 47˚
∠BDC = ∠ADC – ∠ADB
∠BDC = 77˚-47˚
∠BDC = 30˚
(ii) ∠BAD + ∠BCD = 180˚ (Sum of opposite angles of a cyclic quadrilateral is 180˚)
(iii) ∠BCA = ∠ADB = 47˚ (Angles subtended by the same chord on the circle are equal)

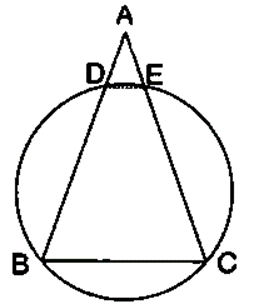
Question 11. In the following figure, O is centre of the circle and ∆ ABC is equilateral. Find:
(i) ∠ADB
(ii) ∠AEB

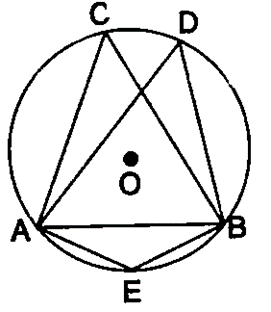
Solution:
∠ACB and ∠ADB are in the same segment
So, ∠ADB = ∠ACB=60˚
Join OA and OB.
∠AOB = 2∠ACB
∠AOB = 2×60˚
∠AOB = 120˚

Question 12. Given — ∠CAB = 75° and ∠CBA = 50°. Find the value of ∠DAB + ∠ABD.

Solution:
In ΔABC,
∠CBA = 50˚
∠CAB = 75˚
∠ACB = 180˚- (∠CBA + ∠CAB)
∠ACB = 180˚ – (∠CBA + ∠CAB)
∠ACB = 180˚ – (50˚ + 75˚)
∠ACB = 180˚ – 125˚
∠ACB = 55˚
∠ADB = ∠ACB = 55˚ (Angle subtended by the same chord on the circle are equal)
Again,
ΔABD,
∠DAB + ∠ABD + ∠ADB = 180˚
∠DAB + ∠ABD + 55˚= 180˚
∠DAB + ∠ABD = 180˚-55˚
∠DAB + ∠ABD = 125˚

Question 13. ABCD is a cyclic quadrilateral in a circle with centre O. If ∠ADC = 130°; find ∠BAC.

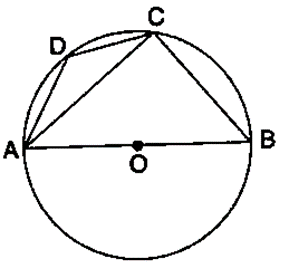
Solution:
We know that,
∠ACB = 90˚ (Angle in a semicircle is right angle)
∠ABC = 180˚ – ∠ADC
∠ABC = 180˚ – 130˚
∠ABC = 50˚ (Pair of opposite angles in a cyclic quadrilateral are supplementary)
∠BAC = 90˚ – ∠ABC
∠BAC = 90˚ – 50˚
∠BAC = 40˚ (by angle sum property of right triangle ACB)

Question 14. In the figure given below, AOB is a diameter of the circle and ∠ AOC = 110°. Find ∠ BDC.

Solution:
Construction:- Join AD
∠ADC = 1/2 ∠AOC
∠ADC = 1/2 × 110˚
∠ADC = 55˚(angle at the centre is double the angle at the circumference subtended by the same chord)
∠ADB = 90˚ (angle in a semicircle is a right angle)
∠BDC = 90˚ – ∠ADC
∠BDC = 90˚ – 55˚
∠BDC = 35˚

Question 15. In the following figure, O is centre of the circle, ∠AOB = 60° and ∠BDC = 100°. Find ∠OBC.

Solution:
Here,
∠ACB = 1/2 ∠AOB
∠ACB = 1/2 × 60˚
∠ACB = 30˚(angle at the centre is double the angle at the circumference subtended by the same chord)
ΔBDC, By angle sum property
∠DBC = 180˚-100˚-30˚
∠DBC = 50˚
Hence, the value of ∠OBC = 50˚

Question 16. ABCD is a cyclic quadrilateral in which ∠ DAC = 27°; ∠ DBA = 50° and ∠ ADB = 33°.
Calculate:
(i) ∠DBC,
(ii) ∠DCB,
(iii) ∠CAB.

Solution:
(i) ∠DBC = ∠DAC = 27˚ (angles subtended by the same chord on the circle are equal)
(ii) ∠ACB = ∠ADB = 33˚ (angles subtended by the same chord on the circle are equal)
∠ACB = ∠ADB = 50˚ (angles subtended by the same chord on the circle are equal)
∠DCB = ∠ACD + ∠ACB
∠DCB = 50˚ + 33˚
∠DCB = 83˚
(iii) ∠DAB + ∠DCB = 180˚ (pair of opposite angles in a cyclic quadrilateral are supplementary)
27˚ + ∠CAB + 83˚ = 180˚
∠CAB = 180˚ – 27˚ – 83˚
∠CAB = 180˚ – 110˚
∠CAB = 70˚

Question 17. In the figure given alongside, AB and CD are straight lines through the centre O of a circle. If ∠AOC = 80° and ∠CDE = 40°. Find the number of degrees in:
(i) ∠DCE;
(ii) ∠ABC.

Solution:
(i) ∠CED = 90˚ (Angle in a semicircle is a right angle)
∠DCE = 90˚-∠CDE
∠DCE = 90˚-40˚
∠DCE = 50˚
∠DCE = ∠OCB = 50˚
(ii) In ΔBOC,
∠AOC = ∠OCB + ∠OBC (Exterior angle of a triangle is equal to the sum of pair of interior opposite angles)
80˚ = 50˚ + ∠OBC
∠OBC = 80-50˚
∠OBC = 30˚

Question 18. In the figure given below, AC is a diameter of a circle, whose centre is O. A circle is described on AO as diameter. AE, a chord of the larger circle, intersects the smaller circle at B. Prove that AB = BE.

Solution:

Construction:- Join OB.
OBA = 90˚ (Angle in a semicircle is a right angle)
OB ⏊ AE
We know, that perpendicular drawn from the centre to a chord bisects the chord.
AB = BE
Hence, AB=BE

Question 19. In the following figure,
(i) if ∠BAD = 96°, find BCD and
(ii) Prove that AD is parallel to FE.

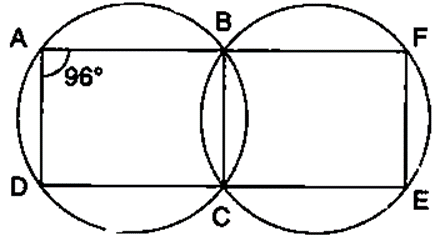
Solution:
(i) ABCD is a cyclic quadrilateral
∠BAD + ∠BCD = 180˚(pair of opposite angles in a cyclic quadrilateral are supplementary)
∠BCD = 180˚-96˚
∠BCD = 84˚
∠BCE = 180˚-84˚
∠BCE = 96˚
Similarly,
BCEF is a cyclic quadrilateral
∠BCE + ∠BFE = 180˚ (pair of opposite angles in a cyclic quadrilateral are supplementary)
96˚ + ∠BFE = 180˚
∠BFE = 180˚ – 96˚
∠BFE = 84˚
(ii) ∠BAD + ∠BFE
= 96˚ + 84˚
= 180˚
These two are interior angles on the same side of a pair of lines AD and EF
AD‖FE┤

Question 20. Prove that:
(i) the parallelogram, inscribed in a circle, is a rectangle.
(ii) the rhombus, inscribed in a circle, is a square.
Solution:
(i)

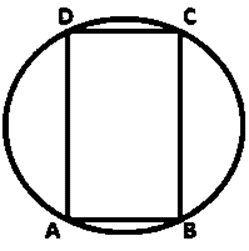
Let ABCD be a parallelogram inscribed in a circle.
∠BAD = ∠BCD (Opposite angle of a parallelogram are equal)
∠BAD + ∠BCD = 180˚ (Pair of opposite angle in a cyclic quadrilateral are supplementary)
∠BAD = ∠BCD = 180˚/2 = 90˚
Similarly, the other two angles are 90˚ and opposite pair of sides are equal.
Hence, ABCD is a rectangle.
(ii)

Let ABCD be a parallelogram inscribed in a circle.
∠BAD = ∠BCD (Opposite angle of a rhombus are equal)
∠BAD+∠BCD = 180˚ (Pair of opposite angle in a cyclic quadrilateral are supplementary)
∠BAD = ∠BCD = 180˚/2 = 90˚
Similarly, the other two angles are 90˚ and all the sides are equal.
Hence, ABCD is a square.

Question 21. In the following figure, AB = AC. Prove that DECB is an isosceles trapezium.

Solution:
AB = AC
∠B = ∠C
Hence, DECB is a cyclic quadrilateral
In a triangle angles opposite to equal sides are equal.
∠B + ∠DEC = 180˚_____ (i) (Pair of opposite angles in a cyclic quadrilateral are supplementary)
∠C + ∠DEC = 180˚ (this is the sum of interior angles on one side of a transversal)
DE || BC
∠ADE = ∠B (corresponding angles)
∠AED = ∠C (corresponding angles)
∠ADE = ∠AED
AD = AE
AB – AD = AC – AE (AB = AC)
BD = CE
We have DE || BC and BD = CE
Therefore, DECB is isosceles trapezium.

Question 22. Two circles intersect at P and Q. Through P diameters PA and PB of the two circles are drawn. Show that the points A, Q and B are collinear. 
Solution:
Let O and O’ be the centers of two intersecting circles,
Where points of intersection are P and Q and PA and PB are their diameters respectively.
Construction:- Join PQ, AQ and QB.
∠AQP = 90˚
∠BQP = 90˚ (angle in a semicircle is a right angle adding both these angles)
∠AQP + ∠BQP = 180˚
∠AQB = 180˚
Therefore, the points A, Q and B are collinear.

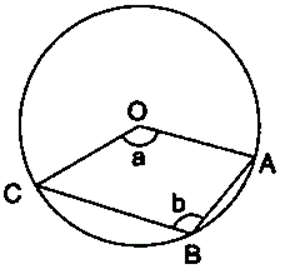
Question 23. The figure given below, shows a circle with centre O. Given: ∠ AOC = a and ∠ ABC = b.
(i) Find the relationship between a and b
(ii) Find the measure of angle OAB, if OABC is a parallelogram.

Solution:
(i) ∠ABC = 1/2 Reflex ∠COA (Angle at the centre is double the angle at the circumference subtended by the same chord)
b = 1/2 (360˚ – a)
2b = 360˚ – a
a + 2b = 180˚
(ii) Since OABC is a parallelogram, so opposite angles are equal
a = b
Using relationship in (i),
3a = 180˚
a = 60˚
Also, OC||BA
∠COA + ∠OAB = 180˚
60˚ + ∠OAB = 180˚
∠OAB = 180˚- 60˚
∠OAB = 120˚

Question 24. Two chords AB and CD intersect at P inside the circle. Prove that the sum of the angles subtended by the arcs AC and BD as the centre O is equal to twice the angle APC. 
Solution:

It is given that, two chords AB and CD intersect each other at P inside the circle. OA, OC and OD are joined.
Need to Prove: – ∠AOC + ∠BOD = 2∠APC
By Construction: – Join AD.
Proof:
Arc AC subtends ∠AOC at the centre and ∠ADC at the remaining part of the circle.
∠AOC = 2∠ADC________(1)
Again,
∠BOD = 2∠BAD________(2)
By adding both the equations,
∠AOC + ∠BOD = 2∠ADC + 2∠BAD
∠AOC + ∠BOD = 2(∠ADC + ∠BAD)___________(3)
In ΔPAD,
∠APC = ∠PAD + ∠ADC
∠APC = ∠BAD + ∠ADC___________(4)
From equation (3) and (4)
∠AOC + ∠BOD = 2∠APC
Hence, the sum of the angles subtended by the arcs AC and BD as the centre O is equal to twice the angle APC.

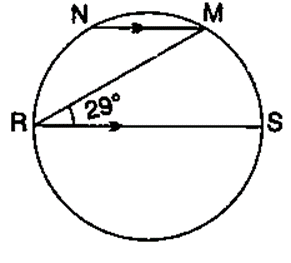
Question 25. In the figure given RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°
Calculate:
(i) ∠RNM;
(ii) ∠NRM.

Solution:
(i) Join RN and MS
∠RMS = 90˚ (Angle in a semicircle is a right angle)
∠RMS = 90˚ – 29˚
∠RMS = 61˚
∠RNM = 180˚ – ∠RSM (by angle sum property of triangle RMS)
∠RNM = 180˚ – 61˚
∠RNM = 119˚ (Pair of opposite angles in a cyclic quadrilateral are supplementary).
(ii) Join RS||NM
∠NMR = ∠MRS = 29˚ (Alternate angles)
∠NMR = 90˚ + 29˚
∠NMR = 119˚
∠NRS + ∠NMS = 180˚ (Pair of opposite angles in cyclic quadrilateral are supplementary)
∠NRM + 29˚ + 119˚ = 180˚
∠NRM + 148˚ = 180˚
∠NRM = 180˚ – 148˚
∠NRM = 32˚

Question 26. In the figure given alongside, AB || CD and O is the centre of the circle. If ∠ ADC = 25°; find the angle AEB. Give reasons in support of your answer.

Solution:
Construction:- Join AC and BD
∠CAD = 90˚ (angle in a semicircle is a right angle)
∠CBD = 90˚ (angle in a semicircle is a right angle)
Also, AB || CD
∠BAD = ∠ADC = 25˚ (Alternate angles)
∠BAC = ∠BAD + ∠CAD
∠BAC = 25˚ + 90˚
∠BAC = 115˚
∠ADB = 180˚ – 25˚ – ∠BAC
∠ADB = 180˚ – 25˚ – 115˚
∠ADB = 40˚ (Pair of opposite angles in a cyclic quadrilateral are supplementary)
∠AEB = ∠ADB = 40˚ (Angle subtended by the same chord on the circle are equal)

Question 27. Two circles intersect at P and Q. Through P, a straight line APB is drawn to meet the circles in A and B. Through Q, a straight line is drawn to meet the circles at C and D. Prove that AC is parallel to BD. 
Solution:

Construction:- Join AC, PQ and BD.
ACQP is a cyclic quadrilateral.
∠CAP + ∠PQC = 180˚_________(1) (Pair of opposite angles in a cyclic quadrilateral are supplementary)
PQDB is a cyclic quadrilateral.
∠PQD + ∠DBP = 180˚_________(2) (Pair of opposite angles in a cyclic quadrilateral are supplementary)
∠PQC + ∠PQD = 180˚_________(3) (CQD is a line)
By Equation (1), (2) and (3)
∠CAP + ∠DBP = 180˚
∠CAB + ∠DBA = 180˚
Hence, we know that, if a transversal line intersects two lines such that a pair of interior angles on the same side of the transversal is supplementary, then the two lines are parallel.
AC || BD.

Question 28. ABCD is a cyclic quadrilateral in which AB and DC on being produced, meet at P such that PA = PD. Prove that AD is parallel to BC. 
Solution:

Let ABCD be the given cyclic quadrilateral.
PA = PD (given)
∠PAD = ∠PDA ______(1)
∠BAD = 180˚ – ∠PAD
∠CDA = 180˚ – ∠PDA
From equation (1)
∠CDA = 180˚ – ∠PAD (we know that the opposite angles of a cyclic quadrilateral are supplementary)
∠ABC = 180 – ∠CDA
∠ABC = 180 – (180˚ – ∠PAD)
∠ABC = 180 – 180 + ∠PAD
∠ABC = ∠PAD
∠ABC = ∠DCB = ∠PAD = ∠PDA
Hence, AD || BC.

Question 29. AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find:
(i) ∠PRB
(ii) ∠PBR
(iii) ∠BPR.

Solution: 
(i) Angle subtended by the same chord on the circle are equal.
∠PRB = ∠PAB = 35˚
(ii) Angle in a semicircle is a right angle
∠BPA = 90˚
∠BPQ = 90˚
∠PBR = ∠BQP + ∠BPQ
∠PBR = 25˚ + 90˚
∠PBR = 115˚ (Exterior angle of a Δ is equal to the sum of pair of interior opposite angles)
(iii) ∠ABP = 90˚ – ∠BAP
∠ABP = 90˚ – 35˚
∠ABP = 55˚
∠ABP = ∠PBR – ∠ABP
∠ABP = 115˚ – 55˚
∠ABP = 60˚
∠APR = ∠ABR = 60˚ (Angle subtended by the same chord on the circle are equal)
∠BPR = 90˚ – ∠APR
∠BPR = 90˚ – 60˚
∠BPR = 30˚

Question 30. In the given figure, SP is the bisector of angle RPT and PQRS is a cyclic quadrilateral. Prove that: SQ = SR.

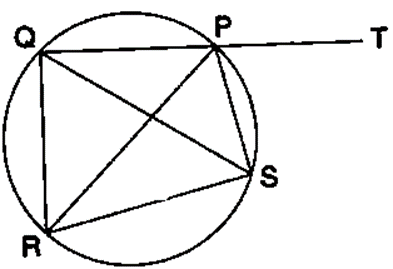
Solution:
It is given that, PQRS is a cyclic quadrilateral
∠QRS + ∠QPS = 180˚___________ (1) (Pair of opposite angles in a cyclic quadrilateral are supplementary)
∠QPS + ∠SPT = 180˚___________ (2) (QPT is a straight line)
From equation (1) and (2)
∠QRS = ∠SPT__________(iii)
∠RQS = ∠RPS__________(iv) (Angle subtended by the same chord on the circle are equal)
∠RPS = ∠SPT___________(v) (PS is bisector or ∠RPT)
From equation (iii), (iv) and (v)
∠QRS = ∠RQS
Hence, SQ = SR

Question 31. In the figure, O is the centre of the circle, ∠AOE = 150°, DAO = 51°. Calculate the sizes of the angles CEB and OCE.

Solutions:

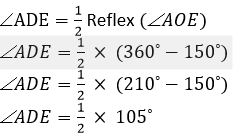
(Angle at the centre is double the angle at the circumference subtended by the same chord)
∠DAB + ∠BED = 180˚ (Pair of opposite angles in a cyclic quadrilateral are supplementary)
∠BED = 180˚ – 51˚
∠BED = 129˚
∠CEB = 180˚ – ∠BED
∠CEB = 180˚ – 129˚
∠CEB = 51˚
By angle sum property we know that,
∠OCE = 180˚ – 51˚ – 105˚
∠OCE = 24˚

Question 32. In the figure, P and Q are the centres of two circles intersecting at B and C. ACD is a straight line. Calculate the numerical value of x.

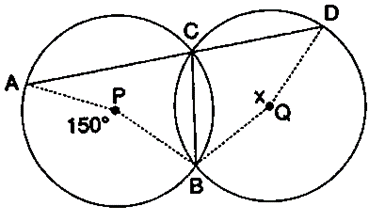
Solution:
∠ACB = 1/2 ∠APB (Angle at the centre is double the angle at the circumference subtended by the same chord)
∠ACB = 1/2 × 150˚
∠ACB = 75˚
∠ACB + ∠BCD = 180˚ (Straight line)
∠BCD = 180˚ – 75˚
∠BCD = 105˚
Also,
∠BCD = 1/2 Reflex ∠BQD
∠BCD = 1/2(360˚-x) (Angle a the centre is double the angle at the circumference subtended by the same chord)
105˚ = 180˚ – x/2
x/2 = 180˚-105˚
x/2 = 75˚
x = 75˚ × 2
x = 150˚

Question 33. The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ∠APB = a°. Calculate, in terms of a°, the value of:
(i) obtuse ∠AOB
(ii) ∠ACB
(iii) ∠ADB.
Give reasons for your answers clearly.

Solution:

(i) It is given that, ∠APB = a˚
obtuse ∠AOB = 2∠APB (Angle at the centre is double the angle at the circumference subtended by the same chord)
obtuse ∠AOB = 2a˚
(ii) OABC is a cyclic quadrilateral
∠AOB + ∠ACB = 180˚ (Pair of opposite angles in a cyclic quadrilateral are supplementary)
∠ACB = 180˚ – 2a˚
(iii) By Construction: Join AB.
∠ADB = ∠ACB
∠ADB = ∠ACB = 180˚ – 2a˚
Angle subtended by the same arc on the circle are equal.

Question 34. In the given figure, O is the centre of the circle and ∠ABC = 55°. Calculate the values of x and y.

Solution:
∠AOC = 2ABC (Angle at the centre is double the angle at the circumference subtended by the same chord)
∠AOC = 2×55˚
∠AOC = 110˚
x = 110˚
ABCD is a cyclic quadrilateral
∠ADC + ∠ABC = 180˚ (Pair of opposite angles in a cyclic quadrilateral are supplementary)
y = 180˚ – 55˚
y = 125˚
Hence, the value of x is 110˚ and y is 125˚

Question 35. In the given figure, A is the centre of the circle, ABCD is a parallelogram and CDE is a straight line. Prove that ∠BCD = 2∠ABE.

Solution:
∠BAD = 2∠BED (angle at the centre is double the angle at the circumference subtended by the same chord)
∠BED = ∠ABE (Alternate angles)
∠BAD = 2∠ABE__________(i)
ABCD is a parallelogram
∠BAD = ∠BCD ___________(ii) (Opposite angles in a parallelogram are equal)
From (i) and (ii)
∠BCD = 2∠ABE

Question 36. ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED = 65°; calculate:
(i) ∠DAB,
(ii) ∠BDC.

Solution:
(i) ∠DAB = ∠BED = 65˚ (Angles subtended by the same chord on the circle are equal)
(ii) ∠ADB = 90˚ (Angles in a semicircle is a right angle)
∠ADB = 90˚ – ∠DAB
∠ADB = 90˚-65˚
∠ADB = 25˚
AB||DC
∠BDC = ∠ABD = 25˚ (Alternate angles)

Question 37. ∠In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠ EAB = 63°; calculate:
(i) ∠EBA,
(ii) BCD.

Solution:
(i) ∠AEB = 90˚ (Angle in a semicircle is a right angle)
Therefore, ∠EBA = 90˚ – ∠EAB
∠EBA = 90˚-63˚
∠EBA = 27˚
(ii) AB || ED
∠DEB = ∠EBA = 27˚ (Alternate angle)
BCDE is a cyclic quadrilateral
∠DEB + ∠BCD = 180˚ (Pair of opposite angles in a cyclic quadrilateral are supplementary)
∠BCD = 180˚-27˚
Hence, ∠BCD = 153˚

Question 38. In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°; calculate:
(i) ∠DAB,
(ii) ∠DBA,
(iii) ∠DBC,
(iv) ∠ADC.
Also, show that the ∆AOD is an equilateral triangle.

Solution:
(i) ABCD is a cyclic quadrilateral
∠DCB + ∠DAB = 180˚ (Pair of opposite angles in a cyclic quadrilateral are supplementary)
∠DAB = 180˚ – 120˚
∠DAB = 60˚
(ii) ∠ADB = 90˚ (Angle in a semicircle is a right angle)
∠DBA = 90˚ – ∠DAB
∠DBA = 90˚ – 60˚
∠DBA = 30˚
(iii) OD = OB
∠ODB = ∠OBD
∠ABD = 30˚
Also, AB || ED
∠DBC = ∠ODB = 30˚ (By Alternate angles)
(iv) ∠ABD + ∠DBC = 30˚ + 30˚
∠ABD + ∠DBC = 60˚
∠ABC = 60˚
In cyclic quadrilateral ABCD.
∠ADC + ∠ABC = 180˚ (pair of opposite angles in a cyclic quadrilateral are supplementary)
∠ADC = 180˚ – 60˚
∠ADC = 120˚
In ΔAOD,
OA = OD (Radius of the circle)
∠AOD = ∠DAO
∠DAB = 60˚
∠AOD = 60˚
∠ADO = ∠AOD = ∠DAO = 60˚
ΔAOD is an equilateral triangle.

Question 39. In the given figure, I is the in centre of the ∆ ABC. BI when produced meets the circum cirle of ∆ ABC at D. Given ∠BAC = 55° and ∠ ACB = 65°, calculate:
(i) ∠DCA,
(ii) ∠DAC,
(iii) ∠DCI,
(iv) ∠AIC.

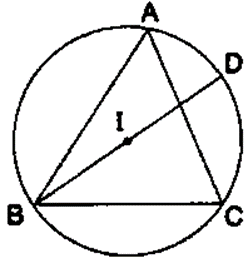
Solution:

Join IA, IC and CD.
(i) IB is the bisector of ÐABC

Question 40. A triangle ABC is inscribed in a circle. The bisectors of angles BAC, ABC and ACB meet the circumcircle of the triangle at points P, Q and R respectively. Prove that:
(i) ∠ABC = 2∠APQ
(ii) ∠ACB = 2∠APR
(iii) ∠QPR = 90° – 1/2BAC

Solution:

Construction: – Join PQ and PR
(i) BQ is the bisector of ∠ABC
∠APQ = 1/2 ∠ABC
∠APQ = ∠ABQ (Angle in the same segment)
∠ABC = 2∠APQ
(ii) CR is the bisector of ∠ACB
∠ACR = 1/2 ∠ACB
∠ACR = ∠APR (Angle in the same segment)
∠ACB = 2∠APR
(iii) By Adding equation (i) and (ii)
∠ABC + ∠ACB = 2∠APQ + 2∠APR
∠ABC + ∠ACB = 2(∠APQ + ∠APR)
∠ABC + ∠ACB = 2∠QPR
180˚ – ∠BAC = 2∠QPR
2∠QPR = 180˚ – ∠BAC

Exercise 17 B

Question 1. In a cyclic-trapezium, the non-parallel sides are equal and the diagonals are also equal. Prove it.

Solution:
It is given that, a cyclic trapezium ABCD in which AB || DC and AC and BD are joined.
Prove: (i) AD = BC (ii) AC = BD
Proof: Chord AD subtends ∠ABD and chord BC subtends ∠BDC at the circumference of the circle.
But ∠ABD = ∠BDC (proved above)
Chord AD = Chord BC
AD = BC
Now in ΔADC and ΔBCD
DC = DC (common)
∠CAD = ∠CBD (angle in the same segment)
AD = BC (proved)
ΔADC≅ΔBCD (SAS congruence rule)
AC = BD (CPCT)

Question 2. In the following figure, AD is the diameter of the circle with centre 0. chords AB, BC and CD are equal. If ∠DEF = 110°, calculate:
(i) ∠AFE,
(ii) ∠FAB.

Solution:

Construction: – Join AE, OB and OC.
(i) Here, AOD is the diameter
∠AED = 90˚ (angle in a semi – circle)
∠DEF = 110˚
∠AEF = ∠DEF – ∠AED
∠AEF = 110˚ – 90˚
∠AEF = 20˚
(ii) Chord AB = Chord BC = Chord CD (given)
∠AOB = ∠BOC = ∠COD (Equal chords subtends equal angle at the centre)
∠AOB + ∠BOC + ∠COD = 180˚ (AOD is a straight line)
∠AOB = ∠BOC = ∠COD = 60˚
In ΔOAB,
OA = OB
Radius of the same circle
∠OAB = ∠OBA
∠OAB + ∠OBA = 180˚ – ∠AOB
∠OAB + ∠OBA = 180˚ – 60˚
∠OAB + ∠OBA = 120˚
∠OAB = ∠OBA = 60˚
In cyclic quadrilateral ADEF,
∠DEF + ∠DAF = 180˚
∠DAF = 180˚ – ∠DEF
∠DAF = 180˚ – 110˚
∠DAF = 70˚
Again,
∠FAB = ∠DAF + ∠OAB
∠FAB = 70˚ + 60˚
∠FAB = 130˚

Question 3. If two sides of a cycle – quadrilateral are parallel; prove that:
(i) its other two side are equal.
(ii) its diagonals are equal.
Solution:

It is given that, ABCD is a cyclic quadrilateral in which AB||DC. AC and BD are diagonals.
Prove: (i) AD = BC (ii) AC = BD
Proof:-
(i) AB || DC
∠DCA = ∠CAB (alternate angle)
Now, chord AD subtends ∠DCA and chord BC subtends ∠CAB at the circumference of the circle.
∠DCA = ∠CAB
Chord AD = Chord BC
AD = BC
(ii) Now in ΔABC and ΔADB,
AB = AB (Common)
∠ACB = ∠ADB (angles in the same segment)
BC = AD (proved)
ΔACB≅ΔADB
AC = BD (CPCT)

Question 4. The given figure show a circle with centre O. also, PQ = QR = RS and ∠PTS = 75°. Calculate:
(i) ∠POS,
(ii) ∠ QOR,
(iii) ∠PQR.

Solution:

Join OP,OQ,OR and OS.
PQ = QR = RS
∠POQ = ∠QOR = ∠ROS (Equal chords subtends equal angles at the centre)
Arc PQRS subtends ∠POS at the centre and ∠PTS at the remaining part of the circle.
∠POS = 2∠PTS
∠POS = 2×75˚
∠POS = 105˚
∠POQ + ∠QOR + ∠ROS = 150˚
∠POQ = ∠QOR = ∠ROS = (150˚)/3
∠POQ = ∠QOR = ∠ROS = 50˚
In ΔOPQ,
OP = OQ (radius of a circle)
∠OPQ = ∠OQP
∠OPQ + ∠OQP + ∠POQ = 180˚
∠OPQ + ∠OQP + 50˚ = 180˚
∠OPQ + ∠OQP = 180˚ – 50˚
∠OPQ + ∠OPQ = 130˚
2∠OPQ = 130˚
∠OPQ = (130˚)/2
∠OPQ = 65˚
Similarly we can prove that,
(i) now ∠POS = 150˚
(ii) ∠QOR = 50˚
(ii) ∠POR = ∠PQO + ∠OQR
∠POR = 65˚ + 65˚
∠POR = 130˚

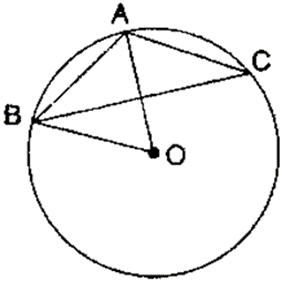
Question 5. In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of:
(i) ∠AOB,
(ii) ∠ACB,
(iii) ∠ABC.

Solution:
(i) Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.
∠ACB = 1/2 ∠AOB
Since AB is the side of a regular hexagon,
∠AOB = 60˚
(ii) ∠AOB = 60˚
∠ACB = 1/2 × 60˚
∠ACB = 30˚

Question 6. In a regular pentagon ABCDE, inscribed in a circle; find ratio between angle EDA and angel ADC.
Solution:

(i) Arc AB subtends ÐAOB at the centre and ÐACB at the remaining part of the circle.

Question 7. In the given figure. AB = BC = CD and ∠ABC = 132°, calculate:
(i) ∠AEB,
(ii) ∠AED,
(iii) ∠COD.

Solution:

In the figure, O is the centre of circle, with AB = BC = CD.
∠ABC = 132˚
(i) In cyclic quadrilateral ABCD,
∠ABC+∠AEC = 180˚ (sum of opposite angles)
132˚+∠AEC = 180˚
∠AEC = 180˚-132˚
∠AEC = 48˚
AB = BC,
∠AEB = ∠BEC (equal chords subtends equal angles)

(ii) Similarly, AB = BC = CD
∠AEB = ∠BED = ∠CED = 24˚
∠AEB = ∠AEB + ∠BEC + ∠CED
∠AEB = 24˚ + 24˚ + 24˚
∠AEB = 72˚
(iii) Arc CD subtends ∠COD at the centre and ∠CED at the remaining part if the circle.
∠COD = 2∠CED
∠COD = 2 × 24˚
∠COD = 48˚

Question 8. In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find:
(i) ∠CAB,
(ii) ∠ADB.

Solution:

∠ACB = 54˚
In cyclic quadrilateral ADBC
∠ADB + ∠ACB = 180˚ (sum of opposite angles)
∠ADB + 54˚ = 180˚
∠ADB = 180˚-54˚
∠ADB = 126˚

Question 9. The figure shows a circle with centre O. AB is the side of regular pentagon and AC is the side of regular hexagon. Find the angles of triangle ABC.

Solution:

Join OA, OB and OC
Since AB is the side of a regular pentagon,
∠AOB = 360˚/5
∠AOB = 72˚
AC is the side of a regular hexagon,
∠AOC = 360˚/6
∠AOC = 60˚
∠AOB + ∠AOC + ∠BOC = 360˚
72˚ + 60˚ + ∠BOC = 360˚
132˚ + ∠BOC = 360˚
∠BOC = 360˚ – 132˚
∠BOC = 228˚
Arc BC subtends ∠BOC at the centre and ∠BAC at the remaining part of the circle.

Question 10. In the given figure, BD is a side of a regular hexagon, DC is a side of a regular pentagon and AD is diameter. Calculate:
(i) ∠ADC
(ii) ∠BAD,
(iii) ∠ABC
(iv) ∠AEC.

Solution:

Join BC, BO, CO and EO
Since BD is the side of a regular hexagon
∠BOD = 360°/6
∠BOD = 60˚
Since DC is the side of a regular pentagon,
∠BOD = (360°)/5
∠BOD = 72˚
In ΔBOD
∠BOD = 60˚ and OB = OD
∠OBD = ∠ODB = 60˚
(i) ΔOCD,∠COD = 72˚ and OC = OD

(iv) In cyclic quadrilateral AECD
∠AEC + ∠ADC = 180˚ (sum of opposite angles)
∠AEC + 54˚ = 180˚
∠AEC = 180˚ – 54˚
∠AEC = 126˚

Exercise 17 C

Question 1. In the given circle with diameter AB, find the value of x.

Solution:
∠ABD = ∠ACD = 30° (Angle in the same segment)
In ∆ADB,
∠BAD + ∠ADB + ∠DBA = 180° (Angles of a A)
∠ADB = 90° (Angle in a semi-circle)
x + 90° + 30° = 180°
x + 120° = 180°
x = 180° – 120°
x = 60°
Hence, the value of x is 60°.

Question 2. In the given figure, ABC is a triangle in which ∠BAC = 30° Show that BC is equal to the radius of the circum-circle of the triangle ABC, whose centre is O.

Solution:

Given that, in the figure ABC is a triangle in which ∠A = 30˚
Need to prove BC is the radius of circumcircle of ΔABC whose centre is O.
Construction: – join OB and OC.
Proof: – ∠BOC = 2∠BAC
∠BOC = 2×30˚
∠BOC = 60˚
Now in ΔOBC,
OB = OC (Radius of the circle)
∠OBC = ∠OCB
In ΔBOC,
∠OBC + ∠OCB + ∠BOC = 180˚ (Angle of a triangle)
∠OBC + ∠OBC + 60˚ = 180˚
2∠OBC = 180˚ – 60˚
2∠OBC = 120˚
∠OBC = (120˚)/2
∠OBC = 60˚
∠OBC = ∠OCB = ∠BOC = 60˚
ΔBOC is an equilateral triangle.
BC = OB = OC
OB and OC are the radius of the circumcircle.
BC is also the radius of the circumcircle.

Question 3. Prove that the circle drawn on any one a the equal side of an isosceles triangle as diameter bisects the base.
Solution:

It is given that, in ΔABC, AB = AC and a circle with AB as diameter is drawn which intersects the side BC and D.
Need to prove D is the mid – point of BC.
By Construction join AD
Proof: – ∠1 = 90˚
∠1 + ∠2 = 180˚ (linear pair)
∠2 + ∠2 = 180˚
2∠2 = 180˚
∠2 = 180˚/2
∠2 = 90˚
In right ΔABD and ΔACD,
AB = AC (Given)
AD = AD (Common)
ΔABD ≅ ΔACD (by RHS congruence rule)
BD = DC (CPCT)
Hence, D is the mid-point of BC.

Question 4. In the given figure, chord ED is parallel to diameter AC of the circle. Given ∠ CBE = 65°, calculate ∠DEC.

Solution:

By Construction Join OE.
EC subtends ∠EOC at the centre and ∠EBC at the remaining part of the circle.
∠EOC = 2∠EBC
∠EOC = 2 × 65˚
∠EOC = 130˚
In ΔOEC,
OE = OC (Radius of the circle)
∠OEC = ∠OCE
In ΔEOC,
∠OEC + ∠OCE + ∠EOC = 180˚ (angle sum property)
∠OCE + ∠OCE + 130˚ = 180˚
2∠OCE = 180˚ – 130˚
2∠OCE = 50˚
∠OCE = 50˚/2
∠OCE = 25˚
AC || ED (given)
∠DEC is Alternate angles of ∠OCE
∠DEC = ∠OCE
∠DEC = 25˚

Question 5. The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
Solution:

It is given that, ABCD is a cyclic quadrilateral and PQRS is a quadrilateral formed by the angle.
By construction bisectors of angle ∠A, ∠B, ∠C and ∠D
Need to prove PQRS is a cyclic quadrilateral.
Proof: –
In ΔAPD,
∠PAD + ∠ADP + ∠APD = 180˚__________(1)
In ΔBQC,
∠QBC + ∠BCQ + ∠BQC = 180˚__________(2)
By adding equation (1) and (2)
∠PAD + ∠ADP + ∠APD + ∠QBC + ∠BCQ + ∠BQC = 180˚ + 180˚
∠PAD + ∠ADP + ∠APD + ∠QBC + ∠BCQ + ∠BQC = 360˚
∠PAD + ∠ADP + ∠QBC + ∠BCQ = 1/2 [∠A + ∠B + ∠C + ∠D]
∠PAD + ∠ADP + ∠QBC + ∠BCQ = 1/2×360˚
∠PAD + ∠ADP + ∠QBC + ∠BCQ = 180˚
∠APD + ∠BQC = 360˚ – 180˚
∠APD + ∠BQC = 180˚
These are the sum of opposite angles of quadrilateral PRQS.
Hence, PQRS is a cyclic quadrilateral.

Question 6. In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate:
(i) ∠BDC
(ii) ∠BEC
(iii) ∠BAC

Solution:
(i) It is given that, BD is a diameter of the circle and ∠DBC = 58˚
The angle in a semicircle is a right angle.
∠BCD = 90˚
In ΔBDC,
∠DBC + ∠BCD + ∠BDC = 180˚
58˚ + 90˚ + ∠BDC = 180˚
148˚ + ∠BDC = 180˚
∠BDC = 180˚¬ – 148˚
∠BDC = 32˚
(ii) We know that the opposite angles of a cyclic quadrilateral are supplementary.
In cyclic quadrilateral BECD,
∠BEC + ∠BDC = 180˚
∠BEC + 32˚ = 180˚
∠BEC = 180˚ – 32˚
∠BEC = 148˚
(iii) In cyclic quadrilateral ABEC,
∠BAC + ∠BEC = 180˚
∠BAC + 148˚ = 180˚
∠BAC = 180˚ – 148˚
∠BAC = 32˚

Question 7. D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Proved that the points B, C, E and D are con – cyclic. 
Solution:

It is given that, In ΔABC, AB = AC and D and E are points on AB and AC such that AD = AE.
Constriction: – Join DE.
Need to Prove: – B,C,E,D are con – cyclic.
Proof:
In ΔABC, AB = AC
∠B = ∠C (angle opposite to equal sides)
Similarly,
In ΔADE,
AD = AE (given)
∠ADE = ∠AED (angle opposite to equal sides)
In ΔABC,
AP/AB = AE/AC
DE || BC
∠ADE = ∠B (Corresponding angles)
∠B = ∠C (proved above)
Ext. ∠ADE = interior opposite ∠C
BCED is a cyclic quadrilateral.
Hence, B, C, E and D are con – cyclic.

Question 8. In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ ADC = 92°, ∠ FAE = 20°; determine ∠ BCD. Given reason in support of your answer.

Solution:
In cyclic quadrilateral ABCD,
AF || CB and DA is produced to E such that ∠ADC = 92˚ and ∠FAE = 20˚
Now we need to find the measure of ∠BCD
In cyclic quadrilateral ABCD,
∠B + ∠D = 180˚
∠B + 92˚ = 180˚
∠B = 180˚ – 92˚
∠B = 88˚
Since AF || CB,∠FAB = ∠B = 88˚
∠FAE = 20˚ (given)
Ext. ∠BAE = ∠BAF + ∠FAE
Ext. ∠BAE = 88˚ + 22˚
Ext. ∠BAE = 108˚
Ext. ∠BAE = ∠BCD
∠BCD = 108˚

Question 9. If I is the in centre of triangle ABC and Al when produced meets the circumcircle of triangle ABC in points D. if ∠BAC = 66° and ∠ABC = 80˚.calculate:
(i) ∠DBC
(ii) ∠IBC
(iii) ∠BIC

Solution:

By construction join DB and DC, IB and IC,
∠BAC = 66˚,∠ABC = 80˚, I is the in centre of the ΔABC,
(i) Since ∠DBC and ∠DAC are in the same segment,
∠DBC = ∠DAC

(iii) ∠BAC = 66˚ and ∠ABC = 80˚
In ΔABC,
∠ACB = 180˚ – (∠ABC + ∠BAC)
∠ACB = 180˚ – (80˚ + 66˚)
∠ACB = 180˚ – (156˚)
∠ACB = 180˚ – 156˚
∠ACB = 34˚
Since IC bisects the ∠C
∠ICB = 1/2 ∠C
∠ICB = 1/2×34˚
∠ICB = 17˚
Now in ΔIBC,
∠IBC + ∠ICB + ∠BIC = 180˚
40˚ + 17˚ + ∠BIC = 180˚
∠BIC = 180˚ – 57˚
∠BIC = 123˚

Question 10. In the given figure, AB = AD = DC = PB and ∠ DBC = x°. Determine, in terms of x:
(i) ∠ABD,
(ii) ∠APB.
Hence or otherwise, prove that AP is parallel to DB.

Solution:

It is given that, In the figure, AB = AD = DC = PB and DBC = x˚
Join AC and BD.
Need to find:- the measure of ∠ABD and ∠APB.
Proof: ∠DAC = ∠DBC = x (angles in the same segment)
∠DCA = ∠DAC = x (AD = DC)
We have,
∠ABD = ∠DAC (angles in the same segment)
In ΔABP,
Ext. ∠ABD = ∠BAP + ∠APB
∠BAP = ∠APB (AB = BP)
2×x = ∠APB + ∠APB
2x = 2∠APB
x = ∠APB
∠APB = ∠DBC = x
These are corresponding angles
Hence, AP‖DB┤

Question 11. In the given figure; ABC, AEQ and CEP are straight lines. Show that ∠APE and ∠ CQE are supplementary.

Solution:

It is given that, in the figure ABC, AEQ and CEP are straight line.
Need to prove: ∠APE + ∠CQE = 180˚
By construction: – Join EB
Proof: –
In cyclic quadrilateral ABEP,
∠APE + ∠ABE = 180˚_________(1)
In cyclic quadrilateral BCQE,
∠CQE + ∠CBE = 180˚_________(2)
By adding (1) and (2) equation,
∠APE + ∠ABE + ∠CQE + ∠CBE = 180˚ + 180˚
∠APE + ∠ABE + ∠CBE = 360˚
∠ABE + ∠CBE = 180˚ (linear pair)
∠APE + ∠CQE + 180˚ = 360˚
∠APE + ∠CQE = 360˚ – 180˚
∠APE + ∠CQE = 180˚
Therefore, ∠APE and ∠CQE are supplementary.

Question 12. In the given, AB is the diameter of the circle with centre O. If ∠ ADC = 32°, find angle BOC.

Solution:

Arc AC subtends ∠AOC at the centre and ∠ADC at the remaining part of the circle.
∠AOC = 2∠ADC
∠AOC = 2 × 32˚
∠AOC = 64˚
Since ∠AOC and ∠BOC are linear pair, we have,
∠AOC + ∠BOC = 180˚
64˚+ ∠BOC = 180˚
∠BOC = 180˚-64˚
∠BOC = 116˚
Hence, the value of ∠BOC is 116˚.

Question 13. In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A: whereas sides PQ and SR produced meet at point B. If ∠A: ∠B = 2 : 1;find angles A and B.

Solution:
PQRS is a cyclic quadrilateral in which ∠PQR = 135˚
Side SP and RQ are produced to meet at A and Side PQ and SR are produced to meet B.
∠A = ∠B = 2:1
Let ∠A = 2x
∠B-x
Now,
In cyclic quadrilateral PQRS,
∠PQR = 135˚
∠S = 180˚-135˚
∠S = 45˚ (Since sum of opposite angle of a cyclic quadrilateral are supplementary)
∠PQR and ∠PQA are linear pair,
∠PQR + ∠PQA = 180˚
135˚ + ∠PQA = 180˚
∠PQA = 180˚-135˚
∠PQA = 45˚
In ΔPBS,
∠P = 180˚-(45˚ + x)
∠P = 180˚-45˚ – x
∠P = 135˚ – x___________(1)
In ΔPQA,
Ext. ∠P = ∠PQA + ∠A
Ext. ∠P = 45˚ + 2x__________(2)
From (1) and (2) we get,
45˚ + 2x = 135˚ – x
2x + x = 135˚ – 45˚
3x = 90˚
x = 90˚/3
x = 30˚
∠A = 2x
∠A = 2×30˚
∠A = 60˚
∠B = x
∠B = 30˚
Hence, the value of ∠A is 60˚ and ∠B is 30˚

Question 14. In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC. If the bisector of angle A meet BC at point E and the given circle at point F, prove that:
(i) EF = FC
(ii) BF = DF

Solution:

It is given that, ABCD is a cyclic quadrilateral in which AD || BC bisector of ∠A meets BC at E and the given circle at F.
DF and BF are joined.
Need to prove:- (i) EF = FC (ii) BF = DF
Proof:- ABCD is a cyclic quadrilateral and AD||BC
AF is the bisector of ∠A, ∠BAF = ∠DAF
∠DAE = ∠BAE
∠DAE = ∠AEB (Alternate angles)
(i) In ΔABE,
∠ABE = 180˚ – 2∠AEB
∠CEF = ∠AEB (Vertically opposite angles)
∠ADC = 180˚ – ∠ABC
∠ADC = 180˚ – (180˚ – 2∠AEB)
∠ADC = 180˚ – 180˚ + 2∠AEB
∠ADC = 2∠AEB (Since ADCF is a cyclic quadrilateral)
∠ECF = 180˚ – (∠AFC + ∠CEF)
∠ECF = 180˚ – (180˚ – 2∠AEB + ∠AEB)
∠ECF = 180˚-180˚ + 2∠AEB – ∠AEB)
∠ECF = ∠AEB
EC = EF
(ii) Arc BF = Arc DF (Equal arcs subtends equal angles)
BF = DF (Equal arcs have equal chords)

Question 15. ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point e; whereas sides BC and AD produced meet at point F. I f ∠ DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
Solution:

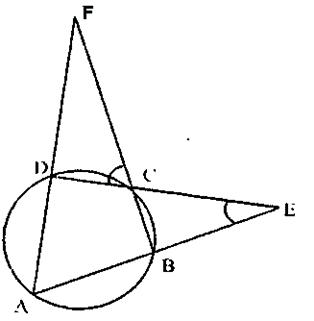
It is given that, in a circle ABCD is a cyclic quadrilateral AB and DC are produced to meet at E and BC and AD are produced to meet at F.
∠DCF: ∠F: ∠E = 3:5:4
Let ∠DCF = 3x
∠F = 5x
∠E = 4x
Now we have to find ∠A, ∠B, ∠C and ∠D
In cyclic quadrilateral ABCD,
BC is produced.
∠A = ∠DCF = 3x
In ΔCDF,
Ext. ∠CDA = ∠DCF + ∠F
Ext. ∠CDA = 3x + 5x
Ext. ∠CDA = 8x
In ΔBCE,
Ext. ∠ABC = ∠BCE + ∠E (∠BCE = ∠DCF) (Vertically opposite angles)
Ext. ∠ABC = ∠DCF + ∠E
Ext. ∠ABC = 3x + 4x
Ext. ∠ABC = 7x
In cyclic quadrilateral ABCD,
∠B + ∠D = 180˚
7x + 8x = 180˚
15x = 180˚
x = 180˚/15
x = 12˚
To find ∠A
∠A = 3x
∠A = 3 × 12˚
∠A = 36˚
To find ∠B
∠B = 7x
∠B = 7 × 12˚
∠B = 84˚
To find ∠C
∠C = 180˚ – ∠A
∠C = 180˚ – 36˚
∠C = 144˚
To find ∠D
∠D = 8x
∠D = 8˚ × 12˚
∠D = 96˚

Question 16. The following figure shows a circle with PR as its diameter. If PQ = 7 cm and QR = 3RS = 6 cm, Find the perimeter of the cyclic quadrilateral PORS.

Solution:
It is given that, In the figure PQRS is a cyclic quadrilateral in which PR is a diameter.
PQ = 7cm
QR = 3RS = 6cm
3RS = 6cm
RS = 2cm
In ΔPQR,
∠Q = 90˚ (Angle in semi circle)
PR² = PQ² + QR² (by Pythagoras theorem)
PR² = (7)² + (6)²
PR² = 49 + 36
PR² = 85
In ΔPSQ,
PR² = PS² + RS² (by Pythagoras theorem)
85 = PS² + (2)²
PS² = 85 – 4
PS² = 81
PS = √81
PS = 9
Perimeter of quadrilateral PQRS = PQ + QR + RS + SP
Perimeter of quadrilateral PQRS = 7 + 9 + 2 + 6
Perimeter of quadrilateral PQRS = 24cm

Question 17. In the following figure, AB is the diameter of a circle with centre O. If chord AC = chord AD. Prove that:
(i) arc BC = arc DB
(ii) AB is bisector of ∠ CAD.
Further if the length of arc AC is twice the length of arc BC find:
(a) ∠BAC
(b) ∠ABC

Solution:

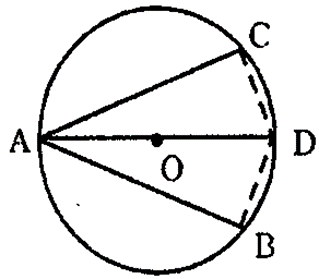
It is given that, in a circle with centre O, AB is the diameter and AC and AD are two chords such that AC = AD.
Need to Prove: – (i) arc BC = arc DB
(ii) AB is the bisector of ∠CAD
(iii) If arc AC = 2arc BC, then find (a) ∠BAC (b) ∠ABC
By construction: – Join BC and BD
Proof: – In right angled ΔABC and ΔABD
AC = AD (given)
AB = AB (common)
∠ADC = ∠ADB (each 90˚)
ΔABC≅ΔABD (By RHS congruence rule)
(i) BC = BD (CPCT)
Arc BC = Arc BD (equal chords have equal arcs)
(ii) ∠BAC = ∠BAD
AB is the bisector of ∠CAD
(iii) If Arc AC = 2 arc BC,
∠ABC = 2∠BAC
∠ABC + ∠BAC = 90˚
2∠BAC + ∠BAC = 90˚
3∠BAC = 90˚
∠BAC = 90˚/3
∠BAC = 30˚

Question 18. In cyclic quadrilateral ABCD; AD = BC, ∠ = 30° and ∠ = 70°; find;
(i) ∠BCD
(ii) ∠BCA
(iii) ∠ABC
(ii) ∠ADC
Solution:

It is given that, ABCD is a cyclic quadrilateral and AD = BC
∠BAC = 30˚
∠CBD = 70˚
We have,
∠DAC = ∠CBD (angles in the same segment)
∠DAC = 70˚ (∠CBD = 70˚)
∠BAD = ∠BAC + ∠DAC
∠BAD = 30˚ + 70˚
∠BAD = 100˚____________(1)
AD = BC, ∠ACD = ∠BDC (equal chords subtends equal angles)
∠ACB = ∠ADB (angles in the same segment)
∠ACD + ∠ACB = ∠BDC + ∠ADB
∠BCD = ∠ADC = 80˚
In ΔBCD,
∠CBD + ∠BCD + ∠BDC = 180˚ (angle sum property)
70˚ + 80˚ + ∠BDC = 180˚
150˚ + ∠BDC = 180˚
∠BDC = 180˚ – 150˚
∠BDC = 30˚
∠ACD = 30˚ (∠ACD = ∠BDC)
∠BCA = ∠BCD – ∠ACD
∠BCA = 80˚ – 30˚
∠BCA = 50˚
∠ADC + ∠ABC = 180˚
80˚ + ∠ABC = 180˚
∠ABC = 180˚ – 80˚
∠ABC = 100˚

Question 19. In the given figure, ∠ACE = 43° and ∠ = 62°; find the values of a, b and c.

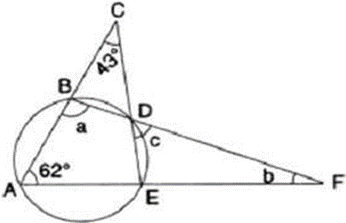
Solution:

It is given that,
∠ACE = 43˚
∠CAF = 62˚
In ΔAEC,
∠ACE + ∠CAE + ∠AEC = 180˚
43˚ + 62˚ + ∠AEC = 180˚
105˚ + ∠AEC = 180˚
∠AEC = 180˚-105˚
∠AEC = 75˚
∠ABD + ∠AED = 180˚
Opposite angles of a cyclic quadrilateral and ∠AED = ∠AEC
a + 75˚ = 180˚
a = 180˚-75˚
a = 105˚
∠EDF = ∠BAE (angles in the alternate segments)
c = 62˚
In ΔBAF,
a + 62˚ + b = 180˚
105˚ + 62˚ + b = 180˚
167˚ + b = 180˚
b = 180˚-167˚
b = 13˚
Hence, the value of a = 105˚, b = 13˚ and c = 62˚

Question 20. In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠ BAC = 25°
Find
(i) ∠CAD
(ii) ∠CBD
(iii) ∠ADC

Solution:

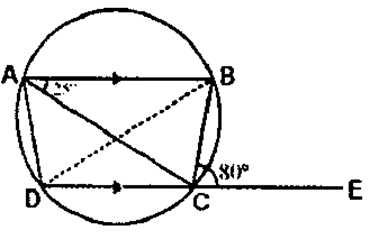
It is given that,
ABCD is a cyclic quadrilateral in which AB||DC. ABCD is an isosceles trapezium
AD = BC
(i) Join BD
We have,
Ext. ∠BCE = ∠BAD (Exterior angle of a cyclic quadrilateral is equal to interior opposite angle)
∠BAD = 80˚
∠BAC = 25˚
∠CAD = ∠BAD – ∠BAC
∠CAD = 80˚ – 25˚
∠CAD = 55˚
(ii) ∠CBD = ∠CAD (angle of the same segment)
∠CBD = 55˚
(iii) ∠ADC = ∠BCD (angles of the isosceles trapezium)
∠ADC = 180˚ – ∠BCE
∠ADC = 180˚ – 80˚
∠ADC = 100˚

Question 21. ABCD is a cyclic quadrilateral of a circle with centre o such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle if AD and BC produced meet at P, show that APB = 60°.
Solution:

It is given that, ABCD is a cyclic quadrilateral in which AB is the diameter and chord CD is equal to the radius of the circle.
Need to prove ∠APB = 60˚
By construction:- join OC and OD
Proof:- chord CD = CO = DO (radius of the circle)
In ΔDOC, (equilateral triangle)
∠DOC = ∠ODC = ∠DCO = 60˚
Let,
∠A = x and ∠B = y
OA = OB = OC = OD (radius of the same circle)
∠ODA = ∠OAD = x
∠OCB = ∠OBC = y
∠AOD = 180˚-2x
∠BOC = 180˚-2y
AOB is a straight line
∠AOD + ∠BOC + ∠COD = 180˚
180˚-2x + 180˚ – 2y + 60˚ = 180˚
2x + 2y = 240˚
2(x + y) = 240˚
x + y = 240˚/2
x + y = 120˚
∠A + ∠B + ∠P = 180˚ (Angles of a triangle)
120˚ + ∠P = 180˚
∠P = 180˚ – 120˚
∠P = 60˚
Hence, ∠APB is 60˚.

Question 22. In the figure, given alongside, CP bisects angle ACB. Show that DP bisects angle ADB.

Solution:
It is given that, in the figure, CP is the bisector of ∠ABC.
Need to prove, DP is the bisector of ∠ADB.
Proof- Since CP is the bisector of ∠ACB
∠ACP = ∠BCP
∠ACP = ∠ADP (angles in the same segment of the circle)
∠BCP = ∠BDP
∠ACP = ∠BCP
∠ADP = ∠BDP
DP is the bisector of ∠ADB.

Question 23. In the figure, given below, AD = BC, ∠ BAC = 30° and ∠ = 70° find:
(i) ∠BCD
(ii) ∠BCA
(iii) ∠ABC
(iv) ∠ADC

Solution:
It is given that, in the figure, ABCD is a cyclic quadrilateral AC and BD are its diagonals.
∠BAC = 30˚
∠CBD = 70˚
Need to Prove: – ∠BCD, ∠BCA, ∠ABC and ∠ADB
∠CAD = ∠CBD = 70˚ (angle in the same segment)
∠BAD = ∠BDC = 30˚
∠BAD = ∠BAC + ∠CAD
∠BAD = 30˚ + 70˚
∠BAD = 100˚
(i) ∠BCD + ∠BAD = 180˚ (opposite angles of cyclic quadrilateral)
∠BCD + ∠BAD = 180˚
∠BCD + 100˚ = 180˚
∠BCD = 180˚ – 100˚
∠BCD = 80˚
(ii) Here, AD = BC, ABCD is an isosceles trapezium and AB||DC
∠BAC = ∠DCA (alternate angles)
∠DCA = 30˚
∠ABC = ∠DCA = 30˚ (angles in the same segment)
∠BCA = ∠BCD – ∠DAC
∠BCA = 80˚ – 30˚
∠BCA = 50˚
(iii) ∠ABC = ∠ABD + ∠CBD
∠ABC = 30˚ + 70˚
∠ABC = 100˚
(iv) ∠ADB = ∠BCA (angle in the same segment)
∠ADB = ∠BCA = 30˚

Question 24. In the figure given below, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°. Find:
(i) ∠OBD
(ii) ∠AOB
(iii) ∠BED
Solution:
(i) AD is parallel to BC
OD is parallel to BC and BD is transversal.
∠ODB = ∠CBD = 32˚ (alternate angles)
In ΔOBD,
OD = OB (Radius of the circle)
∠ODB = ∠OBD = 32˚
(ii) AD is parallel to BC
AO is parallel to BC and OB is transversal.
∠AOB = ∠OBC (Alternate angles)
∠OBC = ∠OBD + ∠DBC
∠OBC = 32˚ + 32˚
∠OBC = 64˚
∠AOB = 64˚
(iii) In ΔOAB,
OA = OB (Radius of the same circle)
Let us assumed that, ∠OAB = ∠OBA = x
∠OAB + ∠OBA + ∠AOB = 180˚
x + x + 64˚ = 180˚
2x + 64˚ = 180˚
2x = 180˚ – 64˚
2x = 116˚
x = 116˚/2
x = 58˚
∠OAB = 58˚
∠DAB = 58˚
∠DAB = ∠BED = 58˚ (angle inscribed in the same arc are equal)

Question 25. In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of
(i) ∠BCD
(ii) ∠BOD
(iii) ∠OBD

Solution:
∠DAE and ∠DAB are linear pair
So,
∠DAE + ∠DAB = 180°
∠DAB = 110°
Also,
∠BCD + ∠DAB = 180° (Opposite angles of cyclic quadrilateral BADC)
∠BCD = 70°
∠BCD = 1/2∠BOD (Angles subtended by an arc on the centre and on the circle)
∠BOD = 140°
In ∆BOD,
OB = OD (Radius of same circle)
So,
∠OBD = ∠ODB (isosceles triangle)
∠OBD+∠ODB+∠BOD = 180° (sum of angles of triangle 2∠OBD = 40°)
∠OBD = 20°
Hence, the value of ∠OBD is 20˚.