Question 1. Draw a circle of radius 3 cm. Mark a point P at a distance of 5 cm from the centre of the circle drawn. Draw two tangents PA and PB to the given circle and measure the length of each tangent.
Solution:

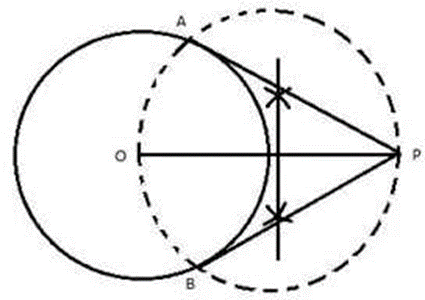
Construction Procedures:
1. Draw a circle with a radius of 3 cm and a center of O.
2. Take a point P from O such that OP = 5 cm.
3. Draw a bisector of OP that passes through M.
4. Draw a circle with a center M and a radius OM that intersects the provided circle at A and B.
5. Assemble AP and BP.
As a result, the tangents AP and BP are necessary. AP = BP = 4 cm as measured
Question 2. Draw a circle of diameter of 9 cm. Mark a point at a distance of 7.5 cm from the centre of the circle. Draw tangents to the given circle from this exterior point. Measure the length of each tangent.
Solution:
Construction Procedures:
1. Make a 9cm radius circle with the letter O in the middle.
2. Outside the circle, draw a line with a point P of 7.5 cm.
3. Draw a circle that intersects the preceding circle at A and B with OP as the diameter.
4. Join PA and PB as a member.
Tangents PA and PB are required as a result. PB = 6 cm.
Question 3. Draw a circle of radius 5 cm. Draw two tangents to this circle so that the angle between the tangents is 45˚.
Solution:
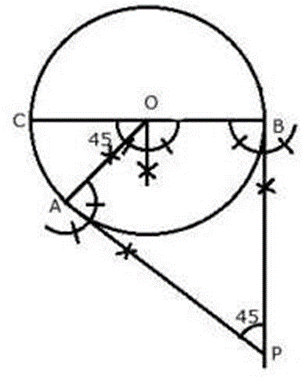
Construction Procedures
1. Draw a circle with a diameter of 5 cm and a diameter of O.
2. At O, draw arcs with an angle of 180˚-45˚=135˚ so that AOB=135˚
3. Draw two rays at each point A and B that meet at point P, outside the circle, at a 90˚ angle.
4. At P, the requisite tangents AP and BP establish a 45˚ angle with each other.
Question 4. Draw a circle of radius 4.5 cm. Draw two tangents to this circle so that the angle between the tangents is 60˚.
Solution:

Construction Procedures:
1. Draw a circle with a radius of 4.5 cm and a radius of O.
2. Draw arcs at O with an angle of 180˚–60˚=120˚, so that AOB=120˚.
3. Draw two rays at A and B that intersect at point P, outside the circle, at a 90˚ angle at each point.
4. At P, the requisite tangents AP and BP form a 60˚ angle with each other.
Question 5. Using ruler and compasses only, draw an equilateral triangle of side 4.5 cm and draw its circumscribed circle. Measure the radius of the circle.
Solution:

Construction Procedures:
1. Draw a BC = 4.5 cm line segment.
2. Draw two arcs of radius 4.5 cm with centers B and C that meet at A.
3. Assemble AC and AB.
4. Make perpendicular bisectors of AC and BC that cross at O.
5. Draw a circle with a center O and a radius OA, OB, or OC that passes through A, B, and C.
This is the triangle ABC’s needed circumcircle. When the radius is measured, it is found to be OA = 2.6 cm.
Question 6. Using ruler and compasses only.
(i) Construct triangle ABC, having given BC = 7 cm, AB – AC = 1 cm and ∠ABC = 45°.
(ii) Inscribe a circle in the ∆ABC constructed in (i) above. Measure its radius.
Solution:

(i) Construction of triangle:
1. Draw a BC = 7 cm line segment.
2. Cut off BE = AB – AC = 1 cm at B by drawing a ray BX at a 45o angle.
3. Draw the perpendicular bisector of EC intersecting BX at A by joining EC.
4. Become an AC member.
The needed triangle is ABC.
(ii) Construction of in circle:
1. Draw angle bisectors for ABC and ACB that overlap at O.
2. Draw perpendiculars from O to BC.
3. Using O as the center and OL as the radius, draw a circle that touches the ABC’s sides. This is the needed ABC in-circle.
4. When measuring, the OL radius was found to be 1.8 cm.
Question 7. Using ruler and compasses only, draw an equilateral triangle of side 5 cm. Draw its inscribed circle. Measure the radius of the circle.
Solution:

Construction Procedures:
1. Draw a BC = 5 cm line segment.
2. Draw two arcs of 5 cm radius each, intersecting at A, with centers B and C.
3. Assemble AB and AC.
4. Create angle bisectors for B and C that intersect at O.
5. Draw OL ⊥ BC from O.
6. Now draw a circle with a center O and a radius OL that touches the edges of ABC. OL = 1.4 cm as measured.
Question 8. Using ruler and compasses only,
(i) Construct a triangle ABC with the following data: Base AB = 6 cm, BC = 6.2 cm and ∠CAB – 60°
(ii) In the same diagram, draw a circle which passes through the points A, B and C and mark its centre as O.
(iii) Draw a perpendicular from O to AB which meets AB in D.
(iv) Prove that AD = BD
Solution:

Construction Procedures:
1. Draw a line segment with the length AB = 6 cm.
2. Draw a ray at A that forms a 60o angle with BC.
3. Draw an arc with B as the center and a radius of 6.2 cm that crosses the AX ray at C.
4. Become a BC member.
The needed triangle is ABC.
Justification:-
1. Draw the crossing perpendicular bisectors of AB and AC at O.
2. Draw a circle that passes through A, B, and C with the center O and the radius OA, OB, or OC.3. From O, draw OD ⊥ AB.
Proof: In right ∆OAD and ∆OBD
OA = OB (radii of same circle)
OD = OD (common)
∆OAD ≅ ∆OBD (RHS)
AD = BD (CPCT)
Question 9. Using ruler and compasses only construct a triangle ABC in which BC = 4 cm, ∠ACB = 45° and perpendicular from A on BC is 2.5 cm. Draw a circle circumscribing the triangle ABC.
Solution:
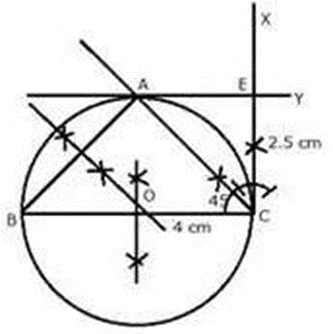
Solution:
Construction Procedures:
1. Draw a BC = 4 cm line segment.
2. Draw a perpendicular line CX at C and cut off CE = 2.5 cm from it.
3. Draw another perpendicular line EY from E.
4. Draw a ray from C that makes a 45˚ angle with CB and intersects EY at A.
5. Become an AB member.
The needed triangle is ABC.
Justification:-
1. Make perpendicular bisectors of the sides AB and BC that intersect at O.
2. With centre O, and radius OB, draw a circle which will pass through A, B and C. Measuring the radius OB = OC = OA = 2 cm
Question 10. Perpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
(i) What do you call the point O?
(ii) What is the relation between the distances OA, OB and OC?
(iii) Does the perpendicular bisector of BC pass through O?
Solution:
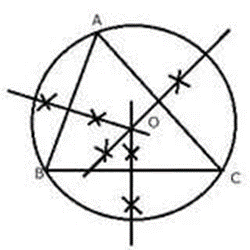
Construction Procedures:
1. O is the circumcentre of the ABC circumcircle.
2. The circumcircle’s radii are OA, OB, and OC.
3. Yes, BC’s perpendicular bisector will traverse O.
Question 11. The bisectors of angles A and B of a scalene triangle ABC meet at O.
(i) What is the point O called?
(ii) OR and OQ are drawn perpendiculars to AB and CA respectively. What is the relation between OR and OQ?
(iii) What is the relation between angle ACO and angle BCO?
Solution:

Construction Procedures:
1. The letter O is referred to as the center of the ABC circle.
2. The radii of the in circle are OR and OQ, and OR = OQ.
3. The bisector of angle C is OC.
∠ACO = ∠BCO.
Question 12. (i) Using ruler and compasses only, construct a triangle ABC in which AB = 8 cm, BC = 6 cm and CA = 5 cm.
(ii) Find its in centre and mark it I.
(iii) With I as centre, draw a circle which will cut off 2 cm chords from each side of the triangle.
Solution:
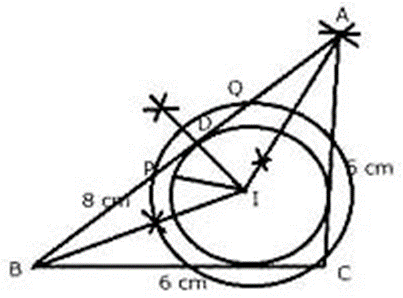
Construction Procedures:
1. Draw a BC = 6 cm line segment.
2. Draw an arc with a radius of 8 cm and a center B.
3. Draw another arc with a radius of 5 cm that meets the first arc at A.
4. Assemble AB and AC.
The needed triangle is ABC.
Justification:-
1. Draw B and A’s angle bisectors intersecting at I. Then there’s me, who’s in the middle of the ABC triangle.
2. Draw ID AB through I.
3. Now from D, cut off DP=DQ=2/2=1cm
4. With centre I, and radius IP or IQ, draw a circle which will intersect each side of triangle ABC cutting chords of 2 cm each.
Question 13. Construct an equilateral triangle ABC with side 6 cm. Draw a circle circumscribing the triangle ABC.
Solution:
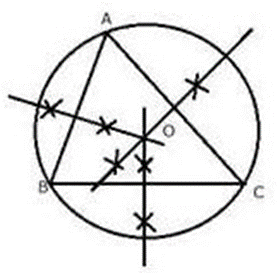
Construction Procedures:
1. Draw a BC = 6 cm line segment.
2. Draw two circles of radius 6 cm that meet at A, with centers B and C.
3. Assemble AC and AB.
4. Make perpendicular bisectors of AC, AB, and BC that intersect at O.
5. Draw a circle with a center O and a radius OA, OB, or OC that passes through A, B, and C.
This is the triangle ABC’s needed circumcircle.
Question 14. Construct a circle, inscribing an equilateral triangle with side 5.6 cm.
Solution:
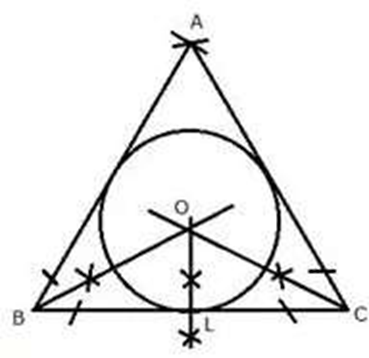
Construction Procedures:
1. Draw a BC = 5.6 cm line segment.
2. Draw two circles of 5.6 cm radius each, intersecting at A, with centers B and C.
3. Assemble AB and AC.
4. Create angle bisectors for B and C that intersect at O.
5. Draw OL BC from O.
6. Now, using the center O and the radius OL, draw a circle that touches the edges of ABC. This is the needed circle.
Question 15. Draw a circle circumscribing a regular hexagon of side 5 cm.
Solution:

Construction Procedures:
1. Draw a regular hexagon ABCDEF with 5 cm on each side and a 120o interior angle.
2. Join the diagonals AD, BE, and CF that cross at O.
3. Draw a circle with the center at O and the radius at OA that passes through the vertices A, B, C, D, E, and F.
4. The needed circumcircle is this.
Question 16. Draw an inscribing circle of a regular hexagon of side 5.8 cm.
Solution:
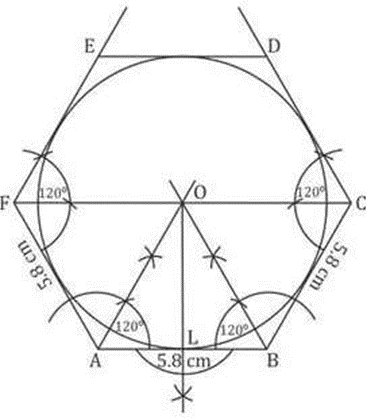
Construction Procedures:
1. Draw a line segment with the length AB = 5.8 cm.
2. Draw rays at an angle of 120° at A and B, and cut off AF = BC = 5.8 cm.
3. Draw rays at an angle of 120° each for F and C, and cut off FE = CD = 5.8 cm.
4. Sign up for DE. The normal hexagon is ABCDEF.
5. Draw the intersection of the bisectors of A and B at O.
6. Draw OL AB from O.
7. Draw a circle with a center O and a radius OL that meets the hexagon’s sides.
This is necessary in the hexagonal circle.
Question 17. Construct a regular hexagon of side 4 cm. Construct a circle circumscribing the hexagon.
Solution:

Construction Procedures:
1. Draw a circle with a radius of 4 cm and a center of O.
2. Draw radii OA and OB so that AOB = 60°, because the internal angle of a regular hexagon is 60˚.
3. On the provided circle, cut out arcs BC, CD, EF, and each equal to arc AB.
4. Join the letters AB, BC, CD, DE, EF, FA to form the needed regular hexagon ABCDEF in a circle.
The hexagon is circumscribed by the circle, which is the requisite circumcircle.
Question 18. Draw a circle of radius 3.5 cm. Mark a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
Solution:

Construction Procedures:
1. Draw a line segment with a length of OP = 6 cm.
2. Draw a circle with a radius of 3.5 cm and a center of O.
3. Draw the OP’s middle.
4. Draw a circle with a center M and a diameter OP that intersects the circle at T and S.
5. Become a member of both PT and PS.
The needed tangents are PT and PS. The length of PT = PS = 4.8 cm was measured.
Question 19. Construct a triangle ABC in which base BC = 5.5 cm, AB = 6 cm and m ∠ABC =120˚.
i.) Construct a circle circumscribing the triangle ABC.
ii.) Draw a cyclic quadrilateral ABCD so that D is equidistant from B and C.
Solution:
i.)

Construction Procedures:
1.) Draw a BC = 5.4 cm line.
2.) Make AB = 6 cm such that mABC = 120 degrees.
3.) Construct AB and BC’s perpendicular bisectors such that they overlap at O.
4.) Make a circle with the radius of O.
ii.)
1.) Extend BC’s perpendicular bisector until it crosses the circle at point D.
2.) Combine the BD and CD.
3.) In this case, BD = DC.
Question 20. Using a ruler and compasses only:
(i) Construct a triangle ABC with the following data: AB = 3.5 cm, BC = 6 cm and ∠ABC = 120°.
(ii) In the same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.
(iii) Measure ∠BCP.
Solution:

Steps of constructions:
1. Draw a BC = 6 cm line segment.
2. At B, draw a ray BX that forms a 120° angle with BC.
3. Cut-off AB = 3.5 cm with B as the center and a radius of 3.5 cm. Come and join AC.
As a result, the needed triangle is ABC.
4. Draw a perpendicular bisector MN of BC via point O. Draw a circle with O as the center and OB as the radius. Draw an ABC angle bisector that intersects the circle at point P. As a result, point P is equidistant from points AB and BC.
5. BCP = 30° as measured
Question 21. Construct a ∆ABC with BC = 6.5 cm, AB = 5.5 cm, AC = 5 cm. Construct the in circle of the triangle. Measure and record the radius of the in circle.
Solution:

Construction Procedures:
1. Make a BC of 6.5 cm.
2. Draw an arc with a radius of 5.5 cm with B as the center.
3. Draw a 5 cm radius arc with C at the center. Allow this arc to intersect with the preceding arc at A.
4. Combine the letters AB and AC to get ABC.
5. Draw the ABC and ACB bi sectors. Allow these bisectors to collide at O.
6. Draw ON ⊥ BC.
7. Draw an in circle that touches all of the edges of ABC with O as the center and radius ON.
8. The radius ON is 1.5 cm when measured.
Question 22. Construct a triangle ABC with AB = 5.5 cm, AC = 6 cm and ∠BAC = 105°. Hence :
(i) Construct the locus of points equidistant from BA and BC.
(ii) Construct the locus of points equidistant from B and C.
(iii) Mark the point which satisfies the above two loci as P. Measure and write the length of PC.
Solution:

Construction Procedures:
1. Draw AB = 5.5 cm on a piece of paper.
2. Create BAR = 105˚.
3. With a radius of 6 cm and a center of A, aut off arc on AR at C.
4. Become a BC member. The needed triangle is ABC.
5. Draw the BD of ABC’s angle bisector, which is the loss of points equidistant between BA and BC.
6. Draw the perpendicular bisector EF of BC, which is the locus of equidistant points between B and C.
7. At point P, BD and EF cross each other. As a result, P meets the first two lod.
PC = 4.8 cm according to measurement
Question 23. Construct a regular hexagon of side 5 cm. Hence construct all its lines of symmetry and name them.
Solution:
Construction Procedures:
1. Using a ruler, draw an AF measuring 5 cm.
2. Draw an arc above AF with A as the center and a radius equal to AF.
3. Cut the previous arc at Z with F as the center and the same radius as before.
4. Draw a circle running between A and F with Z as the center and the same radius.
5. Draw an arc to cut the circle above AF at B with A as the center and the same radius.
6. Draw an arc to cut the circle at C using B as the center and the same radius.
7. Repeat step 7 to retrieve the remaining hexagon vertices at D and E.
8. To make the hexagon, connect successive arcs on the circle.
9. Draw the AF, FE, and DE perpendicular bisectors.
10. Extend AF, FE, and DE bisectors to meet CD, BC, and AB at X, L, and O, respectively.
11. Become a member of AD, CF, and EB.
These are the regular hexagon’s six symmetry lines.

Question 24. Draw a line AB = 5 cm. Mark a point C on AB such that AC = 3 cm. Using a ruler and a compass only, construct:
(i) A circle of radius 2.5 cm, passing through A and C.
(ii) Construct two tangents to the circle from the external point B. Measure and record the length of the tangents.
Solution:

Steps for construction:
1. Using a ruler, draw AB = 5 cm.
2. Cut a 3 cm arc on AB with A as the center to get C.
3. Draw an arc above AB with A as the center and a radius of 2.5 cm.
4. Draw an arc to cut the preceding arc with the same radius and C as the center, and label the junction as O.
5. Draw a circle with O as the center and a radius of 2.5 cm, with points A and C on the circle.
6. Become an OB member.
7. To get the mid-point of OB, M, draw the perpendicular bisector of OB.
8. Draw a circle with the center M and a radius equal to OM to cut the preceding circle at points P and Q.
9. Assemble using PB and QB. The needed tangents to the provided circle from exterior point B are PB and QB = PB = 3 cm.
That is, each tangent is 3 cm long.
Question 25. Using a ruler and a compass construct a triangle ABC in which AB = 7 cm, ∠CAB = 60o and
AC = 5 cm. Construct the locus of
1) points equidistant from AB and AC
2) points equidistant from BA and BC
Hence construct a circle touching the three sides of the triangle internally.
Solution:
Construction Procedures:
1. Draw a line with the length AB = 7 cm.
2. Draw an arc of a circle that crosses AB at M, using P as the center and the same radius.
3. Draw an arc crossing the previously drawn arc at point N, using M as the center and the same radius as before.
4. Draw the ray AX through N, therefore XAB = 60 degrees.
5. Draw an arc cutting AX at C, with A as the center and a radius of 5 cm.
6. Become a BC member.
7. The triangle ABC that is required is acquired.
8. Create an angle bisector between CAB and ABC.
9. Make an O in the middle of their junction.
10. Draw a circle of radius OD with O at the center.
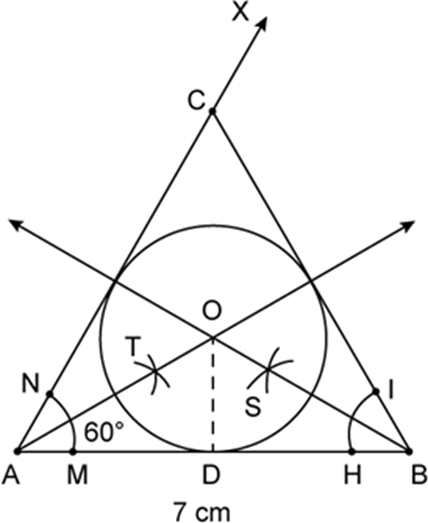
Question 26. Construct a triangle ABC in which AB = 5 cm, BC = 6.8 cm and median AD = 4.4 cm. Draw in circle of this triangle.
Solution:

Steps for construction:
1. Make a BC of 6.8 cm.
2. Draw a line from point D to the mid-point of BC, where BD = DC = 3.4 cm.
3. Draw a line from point D to point B to point A, which is the intersection of arcs AD = 4.4 cm and AB = 5 cm.
4. Assemble AB, AD, and AC. The needed triangle is ABC.
5. Draw the bisectors of angles B and C, which are rays BX and CY, where I is the circle’s center.
6. Make an ABC circle in the shape of a triangle.
Question 27. Draw two concentric circles with radii 4 cm and 6 cm. Taking a point on the outer circle, construct a pair of tangents to inner circle. By measuring the lengths of both the tangents, show that they are equal to each other.
Solution:

Steps for construction:
1. Draw concentric circles of radius 4 cm and 6 cm with centre of O.
2. Take point P on the outer circle.
3. Join OP.
4. Draw perpendicular bisectors of OP where M is the midpoint of OP.
5. Take a distance of a point O from the point M and mark arcs from M on the inner circle it cuts at point A and B respectively.
6. Join PA and PB.
We observe that PA and PB are tangents from outer circle to inner circle are equal of a length 4.5 cm each.
Question 28. In triangle ABC, ∠ABC = 90°, AB = 6 cm, BC = 7.2 cm and BD is perpendicular to side AC. Draw circumcircle of triangle BDC and then state the length of the radius of this circumcircle drawn.
Solution:

Steps for construction:
1. Make a BC of 7.2 cm.
2. Using a compass, draw an angle ABC = 90°.
3. Using a compass, draw BD perpendicular to AC.
4. Become a BD member.
5. Connect the perpendicular bisectors of AB and BC at I, where I is the circle’s circumcentre.
6. Using circumcentre I, draw a circumcircle with a radius of 4.7 cm.


