Question 1. Complete the following table:

Solution:

Question 2. A point P is its own image under the reflection in a line l. Describe the position of point the P with respect to the line l.
Solution:
It is given that, the point P is its own image under the reflection in the line l.
Here point P is a point of invariance.
Hence, the position of point P unchanged.
Question 3. State the co-ordinates of the following points under reflection in x-axis:
(i) (3, 2)
(ii) (-5, 4)
(iii) (0, 0)
Solution:
(i) (3, 2)
Co-ordinate of reflection in the x-axis is (3, -2).
(ii) (-5, 4)
Co-ordinate of reflection in the x-axis is (-5, -4).
(iii) (0, 0)
Co-ordinate of reflection in the x-axis is (0, 0).
Question 4.State the co-ordinates of the following points under reflection in y-axis:
(i) (6, -3)
(ii) (-1, 0)
(iii) (-8, -2)
Solution:
(i) (6, -3)
Co-ordinate of reflection in the y-axis is (-6, -3).
(ii) (-1, 0)
The co-ordinate of reflection in the y-axis is (1, 0).
(iii) (-8, -2)
The co-ordinate of reflection in the y-axis is (8, -2).
Question 5. State the co-ordinates of the following points under reflection in origin:
(i) (-2, -4)
(ii) (-2, 7)
(iii) (0, 0)
Solution:
(i) (-2, -4)
Co-ordinate of reflection in origin is (2, 4).
(ii) (-2, 7)
Co-ordinate of reflection in origin is (2, -7).
(iii) (0, 0)
Co-ordinate of reflection in origin is (0, 0).
Question 6. State the co-ordinates of the following points under reflection in the line x = 0:
(i) (-6, 4)
(ii) (0, 5)
(iii) (3, -4)
Solution:
(i) (-6, 4)
Co-ordinate of reflection in the line x = 0 is (6, 4).
(ii) (0, 5)
Co-ordinate of reflection in the line x = 0 is (0, 5).
(iii) (3, -4)
Co-ordinate of reflection in the line x = 0 is (-3, -4).
Question 7. State the co-ordinates of the following points under reflection in the line y = 0:
(i) (-3, 0)
(ii) (8, -5)
(iii) (-1, -3)
Solution:
(i) (-3, 0)
Co-ordinate of reflection in the line y = 0 is (-3, 0).
(ii) (8, -5)
The co-ordinate of reflection in the line y = 0 is (8, 5).
(iii) (-1, -3)
The co-ordinate of reflection in the line y = 0 is (-1, 3).
Question 8. A point P is reflected in the x-axis. Co-ordinates of its image are (-4, 5).
(i) Find the co-ordinates of P.
(ii) Find the co-ordinates of the image of P under reflection in the y-axis.
Solution:
(i) It is given that, the co-ordinates of image are (-4, 5)
Here, co-ordinates of P are (-4, -5).
(ii) Co-ordinates of reflection in the y-axis (4, -5).
Question 9. A point P is reflected in the origin. Co-ordinates of its image are (-2, 7).
(i) Find the co-ordinates of P.
(ii) Find the co-ordinates of the image of P under reflection in the x-axis.
Solution:
(i) It is given that, the co-ordinates of its image are (-2, 7)
Here, co-ordinates of P are (2, -7).
(ii) Co-ordinates of reflection in the x-axis (2, 7).
Question 10. The point (a, b) is first reflected in the origin and then reflected in the y-axis to P’. If P’ has co-ordinates (4, 6); evaluate a and b.
Solution:
It is given that, (a, b) is first reflected in the origin and then reflected in the y-axis to P’
Co-ordinates of P’ is (4, 6)
We know that, MO (a, b) = (-a, -b)
MY (-a, -b) = (a, -b)
Thus, we get the co-ordinates of the point P’ as (a, -b).
It is given that the co-ordinates of P’ are (4, 6).
Now, by comparing we get, a = 4 and b = -6.
Question 11. The point P (x, y) is first reflected in the x-axis and reflected in the origin to P’. If P’ has co-ordinates (-8, 5); evaluate x and y.
Solution:
It is given that, P (x, y) is first reflected in the x-axis and reflected in the origin to P’.
Co-ordinates of P’ (-8, 5)
We know that, MX (x, y) = (x, -y)
MO (x, -y) = (-x, y)
Thus, we get the co-ordinates of the point P’ as (-x, y).
It is given that the co-ordinates of P’ are (-8, 5).
Now, by comparing we get, x = 8 and y = 5
Question 12. The point A (-3, 2) is reflected in the x-axis to the point A’. Point A’ is then reflected in the origin to point A”.
(i) Write down the co-ordinates of A”.
(ii) Write down a single transformation that maps A onto A”.
Solution:
(i) It is given that, the point A (-3, 2) is reflected in the x-axis
Here, reflection in x-axis MX (x, y) = (x, -y).
A’ = reflection of A (-3, 2) in the x- axis = (-3, -2).
The reflection in origin is given by MO (x, y) = (-x, -y).
A” = reflection of A’ (-3, -2) in the origin = (3, 2)
Hence, the reflection of A’ is (-3,-2) and A’’ is (3, 2).
(ii) Here, the reflection in y-axis is given by MY (x, y) = (-x, y).
The reflection of A (-3, 2) in y-axis is (3, 2).
Hence, the single transformation is the reflection of A in the y-axis to the point A”.
Question 13. The point A (4, 6) is first reflected in the origin to point A’. Point A’ is then reflected in the y-axis to the point A”.
(i) Write down the co-ordinates of A”.
(ii) Write down a single transformation that maps A onto A”.
Solution:
(i) It is given that, The point A (4, 6) is first reflected in the origin to point A’
Here, reflection in origin MO (x, y) = (-x, -y).
A’ = reflection of A (4, 6) in the origin = (-4, -6)
The reflection in y-axis is given by MY (x, y) = (-x, y).
A” = reflection of A’ (-4, -6) in the y-axis = (4, -6)
(ii) Here, reflection in x-axis is given by MX (x, y) = (x, -y).
The reflection of A (4, 6) in x-axis is (4, -6).
Hence, the single transformation is the reflection of A in the x-axis to the point A”.
Question 14. The triangle ABC, where A is (2, 6), B is (-3, 5) and C is (4, 7), is reflected in the y-axis to triangle A’B’C’. Triangle A’B’C’ is then reflected in the origin to triangle A”B”C”.
(i) Write down the co-ordinates of A”, B” and C”.
(ii) Write down a single transformation that maps triangle ABC onto triangle A”B”C”.
Solution:
(i) It is given that, triangle ABC, where A is (2, 6), B is (-3, 5) and C is (4, 7).
We know that, Reflection in y-axis is given by MY (x, y) = (-x, y)
A’ = Reflection of A (2, 6) in y-axis = (-2, 6)
B’ = Reflection of B (-3, 5) in y-axis (3, 5)
C’ = Reflection of A (4, 7) in y-axis (-4, 7)
(ii) Reflection in origin is given by MO (x, y) = (-x, -y)
A” = Reflection of A’ (-2, 6) in origin = (2, -6)
B” = Reflection of B’ (3, 5) in origin (-3, -5)
C” = Reflection of C’ (-4, 7) in origin (4, -7)
Hence, Single transformation which maps triangle ABC to triangle A”B”C” is reflection in x- axis.
Question 15. P and Q have co-ordinates (-2, 3) and (5, 4) respectively. Reflect P in the x-axis to P’ and Q in the y-axis to Q’. State the co-ordinates of P’ and Q’.
Solution:
It is given that, P and Q have co-ordinates (-2, 3) and (5, 4).
Reflection in x-axis is given by MX (x, y) = (x, -y)
P’ = Reflection of P (-2, 3) in x-axis = (-2, -3)
Reflection in y-axis is given by MY (x, y) = (-x, y)
Q’ = Reflection of Q (5, 4) in y-axis = (-5, 4)
Hence, the co-ordinates of points P’ and Q’ are (-2, -3) and (-5, 4) respectively.
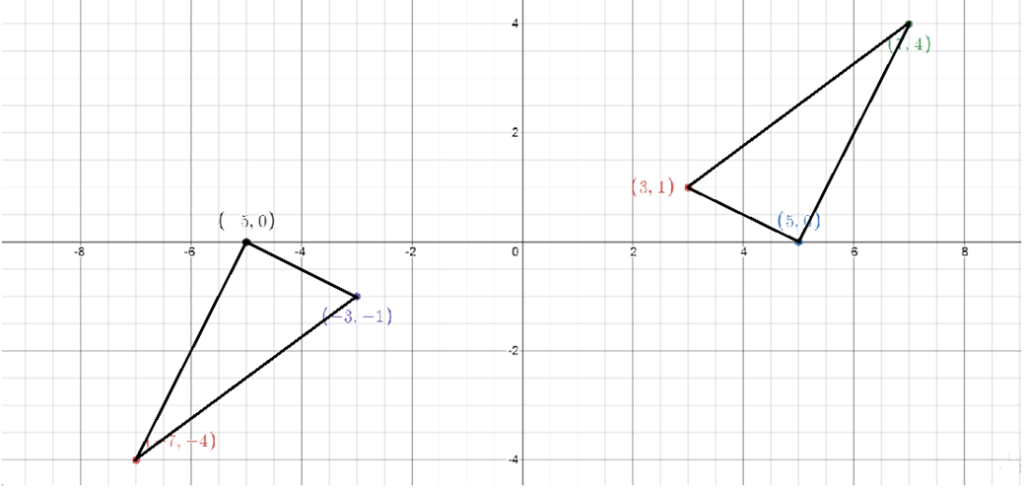
Question 16. On a graph paper, plot the triangle ABC, whose vertices are at points A (3, 1), B (5, 0) and C (7, 4). On the same diagram, draw the image of the triangle ABC under reflection in the origin O (0, 0).
Solution:
Below is the graph shows ∆ABC and ∆A’B’C’.
Question 17. Find the image of point (4, -6) under the following operations:
(i) MX . My
(ii) My . Mx
(iii) MO . Mx
(iv) Mx . MO
(v) MO . My
(vi) My . MO
Write down a single transformation equivalent to each operation given above. State whether:
(a) MO . Mx = Mx . MO
(b) My . MO = MO . My
Solution:
(i) MX . MY (4, -6) = MX (-4, -6) = (-4, 6)
Hence, Single transformation equivalent to MX . MY is MO.
(ii) My . Mx (4, -6) = My (4, 6) = (-4, 6)
Hence, Single transformation equivalent to MY . MX is MO.
(iii) MO . Mx (4, -6) = MO (4, 6) = (-4, -6)
Hence, Single transformation equivalent to MO . Mx is My.
(iv) Mx . MO (4, -6) = Mx (-4, 6) = (-4, -6)
Hence, Single transformation equivalent to Mx . MO is My.
(v) MO . My (4, -6) = MO (-4, -6) = (4, 6)
Hence, Single transformation equivalent to MO . My is Mx.
(vi) My . MO (4, -6) = My (-4, 6) = (4, 6)
Hence, Single transformation equivalent to Mx . MO is Mx.
From (iii) and (iv), it is clear that MO . Mx = Mx . MO.
From (v) and (vi), it is clear that My . MO = MO . My.
Question 18. Point A (4, -1) is reflected as A’ in the y-axis. Point B on reflection in the x-axis is mapped as B’ (2, 5). Write down the co-ordinates of A’ and B.
Solution:
Reflection in y-axis is given by MY (x, y) = (-x, y)
A’ = Reflection of A(4, -1) in y-axis = (-4, -1)
Reflection in x-axis is given by Mx (x, y) = (x, -y)
B’ = Reflection of B in x-axis = (-2, 5)
Hence, the co-ordinate of A’ is (-4,-1) and B is (-2, -5)
Question 19. The point (-5, 0) on reflection in a line is mapped as (5, 0) and the point (-2, -6) on reflection in the same line is mapped as (2, -6).
(a) Name the line of reflection.
(b) Write down the co-ordinates of the image of (5, -8) in the line obtained in (a).
Solution:
(a) It is given that, point (-5, 0) on reflection in a line is mapped as (5, 0).
We know that reflection in the line x = 0 is the reflection in the y-axis.
Point (-2, -6) on reflection in the same line is mapped as (2, -6).
Hence, the line of reflection is x = 0.
(b) We know that, MY (x, y) = (-x, y)
Hence, Co-ordinates of the image of (5, -8) in the line x = 0 are (-5, -8).
Exercise 12B
Question 1. Attempt this question on graph paper.
(a) Plot A (3, 2) and B (5, 4) on graph paper. Take 2 cm = 1 unit on both the axes.
(b) Reflect A and B in the x-axis to A’ and B’ respectively. Plot these points also on the same graph paper.
(c) Write down:
(i) the geometrical name of the figure ABB’A’;
(ii) the measure of angle ABB’;
(iii) the image of A” of A, when A is reflected in the origin.
(iv) the single transformation that maps A’ to A”.
Solution:
(a) (b)
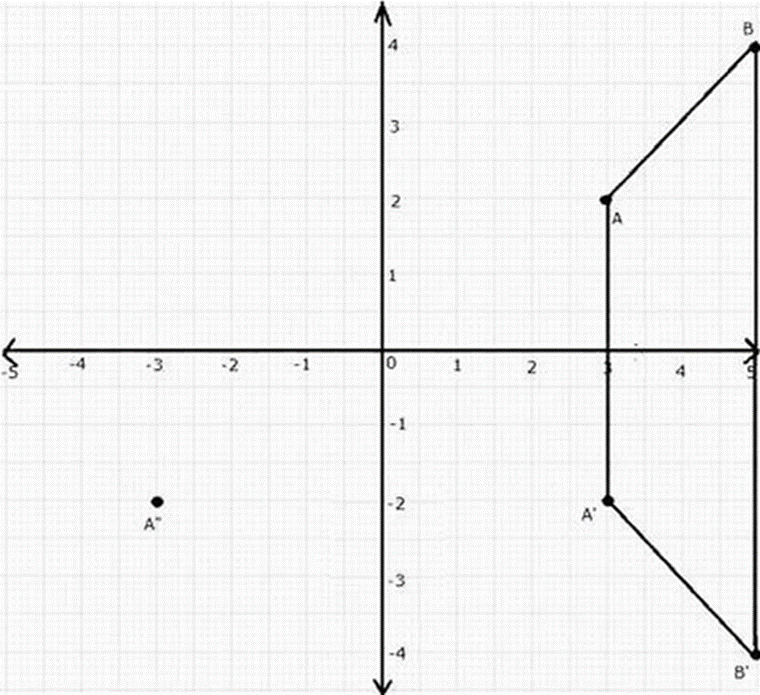
c) (i) The geometrical name of the figure ABB’A’ is an isosceles trapezium.
(ii) The measure of angle ABB’ is 45°.
(iii) The image of A” of A, when A is reflected in the origin is A” = (-3, -2)
(iv) The reflection of y-axis in single transformation that maps A’ to A”.
Question 2. Points (3, 0) and (-1, 0) are invariant points under reflection in the line L1; points (0, -3) and (0, 1) are invariant points on reflection in line L2.
(i) Name or write equations for the lines L1 and L2.
(ii) Write down the images of the points P (3, 4) and Q (-5, -2) on reflection in line L1. Name the images as P’ and Q’ respectively.
(iii) Write down the images of P and Q on reflection in L2. Name the images as P” and Q” respectively.
(iv) State or describe a single transformation that maps P’ onto P”.
Solution:
(i) It is given that, points (3, 0) and (-1, 0) lie on the x-axis.
(3, 0) and (-1, 0) are invariant under reflection in x-axis.
Hence, the equation of line L1 is y = 0.
(0, -3) and (0, 1) are invariant under reflection in y-axis.
Hence, the equation of line L2 is x = 0.
(ii) P’ = Image of P (3, 4) in L1 = (3, -4)
Q’ = Image of Q (-5, -2) in L1 = (-5, 2)
(iii) P” = Image of P (3, 4) in L2 = (-3, 4)
Q” = Image of Q (-5, -2) in L2 = (5, -2)
(iv) In origin, the single transformation that maps P’ to P” is reflection.
Question 3. (i) Point P (a, b) is reflected in the x-axis to P’ (5, -2). Write down the values of a and b.
(ii) P” is the image of P when reflected in the y-axis. Write down the co-ordinates of P”.
(iii) Name a single transformation that maps P’ to P”.
Solution:
(i) It is given that, Point P (a, b) is reflected in the x-axis to P’ (5, -2).
We know that, MX (x, y) = (x, -y)
P’ (5, -2) = reflection of P (a, b) in x-axis.
Co-ordinates of P are (5, 2).
Hence, the values of a is 5 and b is 2.
(ii) It is given that, P” is the image of P when reflected in the y-axis
P” = image of P (5, 2) reflected in y-axis
Hence, the value of P” is (-5, 2).
(iii) The reflection in origin is a single transformation that transfers P’ to P”.
Question 4. The point (-2, 0) on reflection in a line is mapped to (2, 0) and the point (5, -6) on reflection in the same line is mapped to (-5, -6).
(i) State the name of the mirror line and write its equation.
(ii) State the co-ordinates of the image of (-8, -5) in the mirror line.
Solution:
(i) It is given that, point (-2, 0) on reflection in a line is mapped to (2, 0) and the point (5, -6) on reflection in the same line is mapped to (-5, -6).
We know reflection of a point (x, y) in y-axis is (-x, y).
The point (-2, 0) when reflected in y-axis is (2, 0).
Hence, the mirror line is the y-axis and its equation is x = 0.
(ii) Co-ordinates of the image of (-8, -5) in the mirror line are (8, -5).
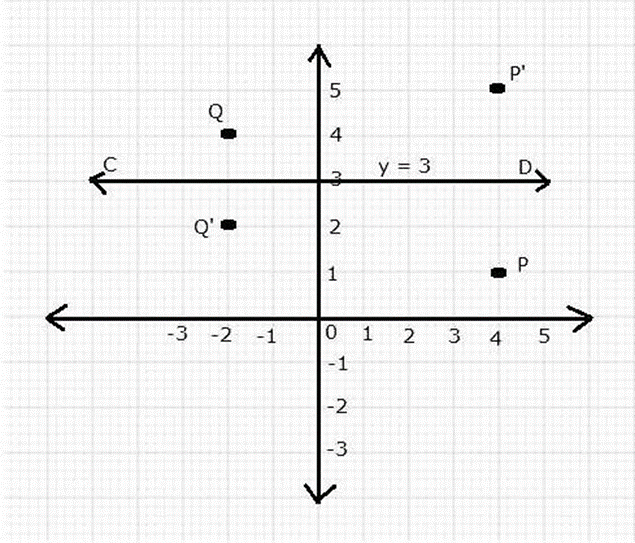
Question 5. The points P (4, 1) and Q (-2, 4) are reflected in line y = 3. Find the co-ordinates of P’, the image of P and Q’, the image of Q.
Solution:
It is given that, the points P (4, 1) and Q (-2, 4) are reflected in line y = 3.
Mark points P (4, 1) and Q (-2, 4).
Draw a straight line parallel to line CD from P and create. Make a point P’ on this line that is the same distance above CD as P is below it. The co-ordinates of P’ are (4, 5).
Draw a line parallel to CD from Q and mark point Q’, which is the same distance below CD as Q is above it. The co-ordinates of Q’ are (-2, 2).
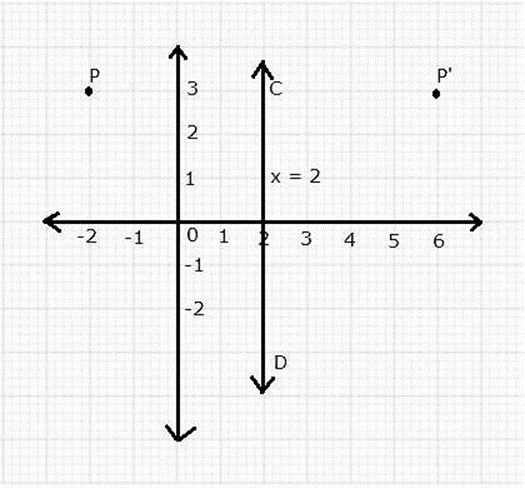
Question 6. A point P (-2, 3) is reflected in line x = 2 to point P’. Find the coordinates of P’.
Solution:
The line x = 2 is a line that runs parallel to the y-axis and is 2 units away from it. Make a note of point P. (-2, 3).
Draw a straight line parallel to line CD from P and create. Make a point P’ on this line that is the same distance to the right of CD as P is to the left. P’s coordinates are as follows: (6, 3).
Question 7. A point P (a, b) is reflected in the x-axis to P’ (2, -3). Write down the values of a and b. P” is the image of P, reflected in the y-axis. Write down the co-ordinates of P”. Find the co- ordinates of P”’, when P is reflected in the line, parallel to y-axis, such that x = 4.
Solution:
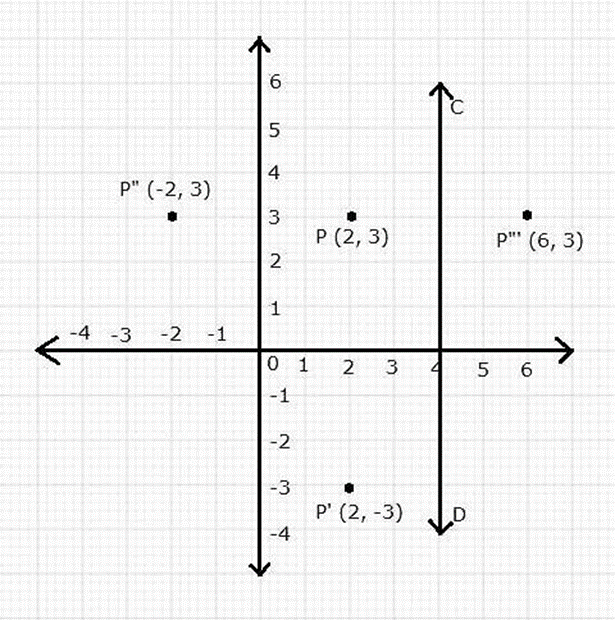
The x-axis reflects a point P (a, b) to P’ (2, -3). We already know that Mx (x, y) = (x, -y) As a result, P’s coordinates are (2, 3). As a result, a = 2 and b = 3.
P” = Image of P reflected in the y-axis = (-2, 3)
P”’ = Reflection of P in the line (x = 4) = (6, 3)
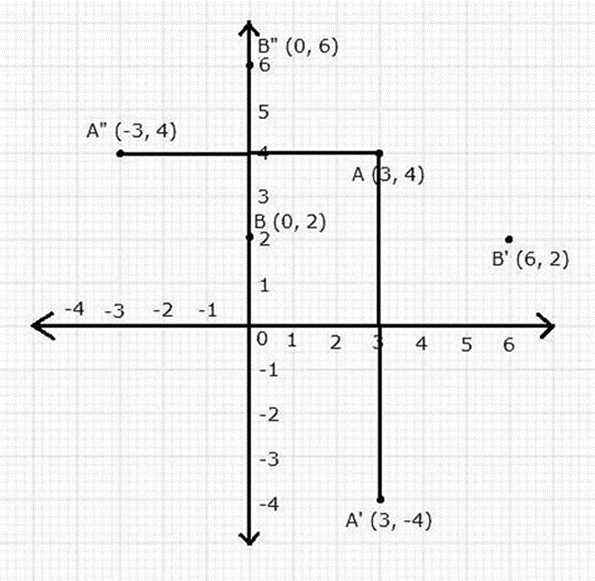
Question 8. Points A and B have co-ordinates (3, 4) and (0, 2) respectively. Find the image:
(a) A’ of A under reflection in the x-axis.
(b) B’ of B under reflection in the line AA’.
(c) A” of A under reflection in the y-axis.
(d) B” of B under reflection in the line AA”.
Solution:
It is given that, Points A and B have co-ordinates (3, 4) and (0, 2).
(a) A’ = A under reflection in the x-axis = (3, -4)
(b) B’ = B under reflection in the line AA’ = (6, 2)
(c) A” = A under reflection in the y-axis = (-3, 4)
(d) B” = B under reflection in the line AA” = (0, 6)
Question 9. (i) Plot the points A (3, 5) and B (-2, -4). Use 1 cm = 1 unit on both the axes.
(ii) A’ is the image of A when reflected in the x-axis. Write down the co-ordinates of A’ and plot it on
the graph paper.
(iii) B’ is the image of B when reflected in the y-axis, followed by reflection in the origin. Write down the co-ordinates of B’ and plot it on the graph paper.
(iv) Write down the geometrical name of the figure AA’BB’.
(v) Name the invariant points under reflection in the x-axis.
Solution:
(i) The points A (3, 5) and B (-2, -4) can be plotted on a graph as shown.
(ii) The co-ordinates of A’ of Image of A when reflected in the x-axis is (3, -5)
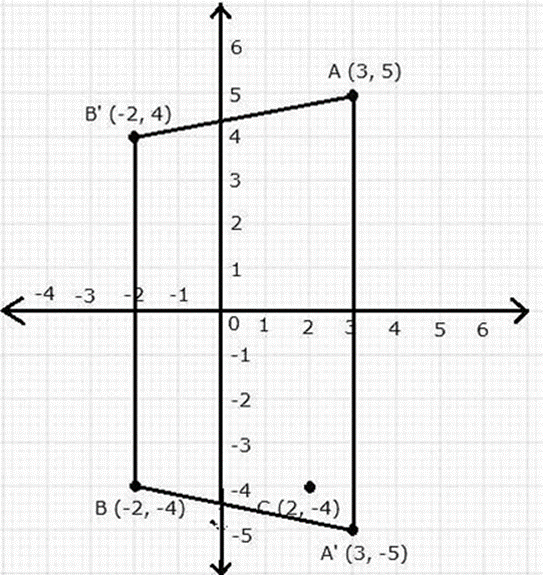
(iii) C = Image of B when reflected in the y-axis = (2, -4) B’ = Image when C is reflected in the origin =
(-2, 4).
(iv) The geometrical name of the figure AA’BB’ is Isosceles trapezium.
(v) A point that does not change as a result of a transformation is called an invariant. As a consequence, the two points required are (3, 0) and (3, 0). (0, -2).
Question 10. The point P (5, 3) was reflected in the origin to get the image P’.
(a) Write down the co-ordinates of P’.
(b) If M is the foot if the perpendicular from P to the x-axis, find the co-ordinates of M.
(c) If N is the foot if the perpendicular from P’ to the x-axis, find the co-ordinates of N.
(d) Name the figure PMP’N.
(e) Find the area of the figure PMP’N.
Solution:
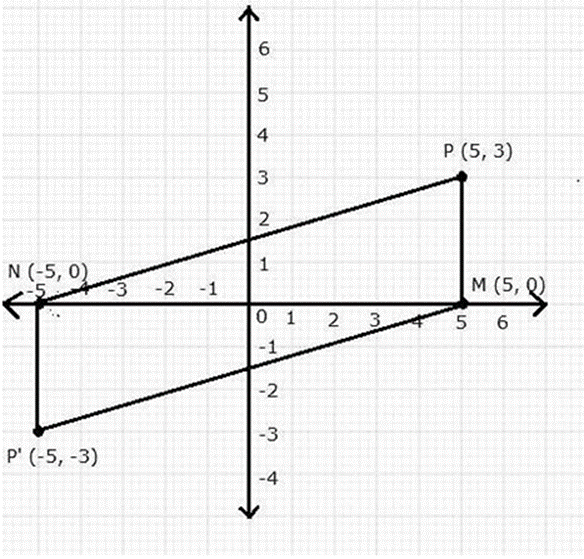
(a) The co-ordinates of P’ = (-5, -3)
(d) The Co-ordinates of M = (5, 0)
(c) The Co-ordinates of N = (-5, 0)
(d) The figure PMP’N is a parallelogram.
(e) Area of PMP’N = 2 (Area of DPMN)
= 2 × 1/2 × 10 × 3
= 30 sq. units
Question 11. The point P (3, 4) is reflected to P’ in the x-axis; and O’ is the image of O (the origin) when reflected in the line PP’. Write:
(i) the co-ordinates of P’ and O’.
(ii) the length of the segments PP’ and OO’.
(iii) the perimeter of the quadrilateral POP’O’.
(iv) the geometrical name of the figure POP’O’.
Solution:
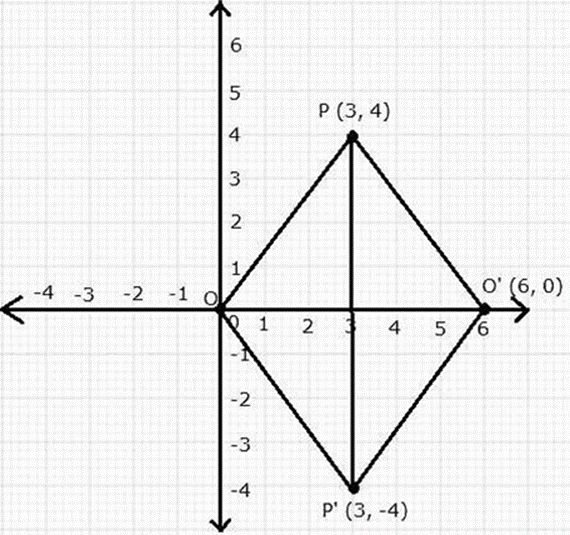
(i) Co-ordinates of P’ and O’ are (3, -4) and (6, 0) respectively.
(ii) PP’ = 8 units and OO’ = 6 units.
(iii) From the graph it is clear that all sides of the quadrilateral POP’O’ are equal. In right Δ PO’Q,
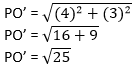
PO’= 5 units
Perimeter of quadrilateral POP’O’ = 4 PO’
Perimeter of quadrilateral POP’O’= 4 × 5 units
Perimeter of quadrilateral POP’O’= 20 units
Hence, the Perimeter of quadrilateral POP’O’ is 20 units.
(iv) The geometrical name of the figure POP’O’ is a rhombus.
Question 12. A (1, 1), B (5, 1), C (4, 2) and D (2, 2) are vertices of a quadrilateral. Name the quadrilateral ABCD. A, B, C, and D are reflected in the origin on to A’, B’, C’ and D’ respectively. Locate A’, B’, C’ and D’ on the graph sheet and write their co-ordinates. Are D, A, A’ and D’ collinear?
Solution:
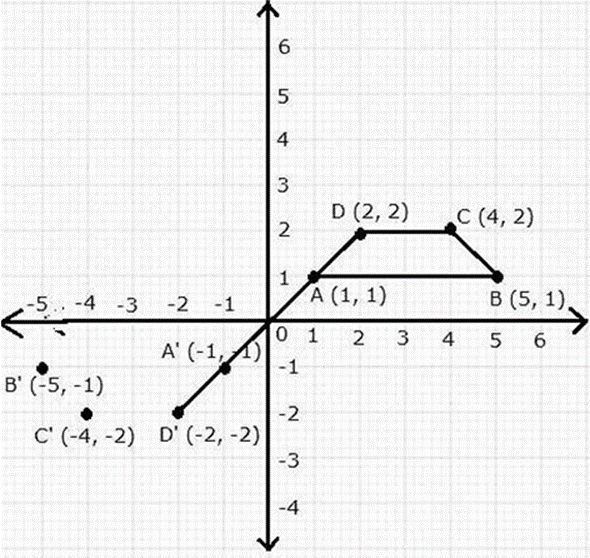
The Quadrilateral ABCD is an isosceles trapezium. Co-ordinates of A’, B’, C’ and D’ are A'(-1, -1), B'(-5, -1), C'(-4, -2) and D'(-2, -2) respectively. It is clear from the graph that D, A, A’ and D’ are collinear.
Question 13. P and Q have co-ordinates (0, 5) and (-2, 4).
(a) P is invariant when reflected in an axis. Name the axis.
(b) Find the image of Q on reflection in the axis found in (i).
(c) (0, k) on reflection in the origin is invariant. Write the value of k.
(d) Write the co-ordinates of the image of Q, obtained by reflecting it in the origin followed by reflection in x-axis.
Solution:
(a) An invariant is a point that does not change as a result of a transformation. When reflected on an axis, P (0, 5) is known to be invariant. When P is mirrored in the y-axis, it is obvious that it will stay invariant. As a result, the y-axis is necessary.
(b) The co-ordinates of the image of Q (-2, 4) when reflected in y-axis is (2, 4).
(c) On reflection in the origin, (0, k) is invariant. The reflection of origin in origin is unchanging, as we know. As a result, k = 0.
(d) When reflected in origin, the image of Q (-2, 4) has the coordinates = (2, -4) When the image of (2, -4) is mirrored in the x-axis = (2, 4). As a result, the point’s co-ordinates are (2, 4).
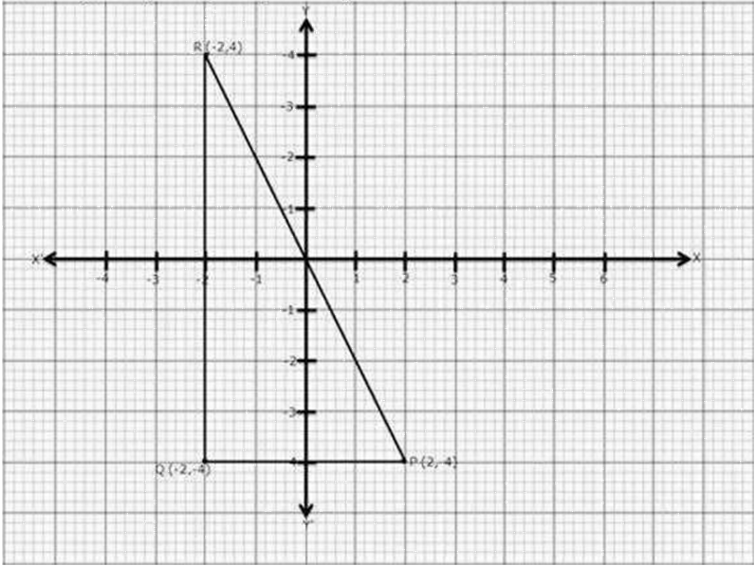
Question 14. (i) The point P (2, -4) is reflected about the line x = 0 to get the image Q. Find the co- ordinates of Q.
(ii) The point Q is reflected about the line y = 0 to get the image R. Find the co-ordinates or R.
(iii) Name the figure PQR.
(iv) Find the area of figure PQR.
Solution:
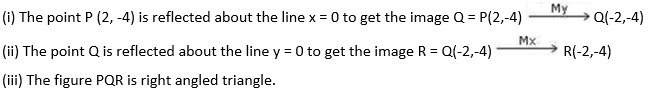

Question 15. Using a graph paper, plot the point A (6, 4) and B (0, 4).
(a) Reflect A and B in the origin to get the image A’ and B’.
(b) Write the co-ordinates of A’ and B’.
(c) Sate the geometrical name for the figure ABA’B’.
(d) Find its perimeter.
Solution:
(a)
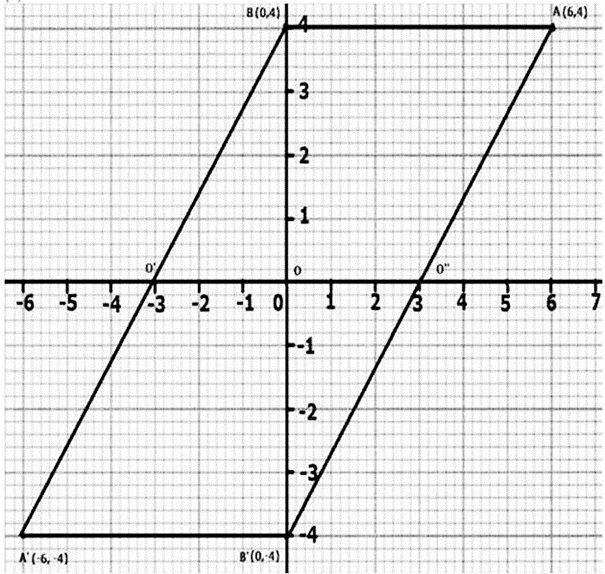
(b) Co-ordinates of A’ = (-6,-4)
Co-ordinates of B’ = (0,-4)
(c) ABA’B’ is a parallelogram.
(d) In ∆BA’B, BB’ = 8 units
A’B’ = 6 units
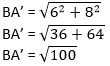
BA’ = 10 units
B’A = 10 units
AB = A’B’ 6 units
Perimeter of ABA’B’ = AB + BA’ + A’B’ + B’A
Perimeter of ABA’B’ = 6 + 10 + 6 + 10
Perimeter of ABA’B’ = 32 units
Question 16. Use graph paper for this question. (Take 2 cm = 1 unit along both x and y axis. Plot the points O (0, 0), A (-4, 4), B (-3, 0) and C (0, -3).
(i) Reflect points A and B on the y-axis and name them A’ and B’ respectively. Write down their coordinates.
(i) Name the figure OABCB’A’.
(ii) State the line of symmetry of this figure.
Solution:
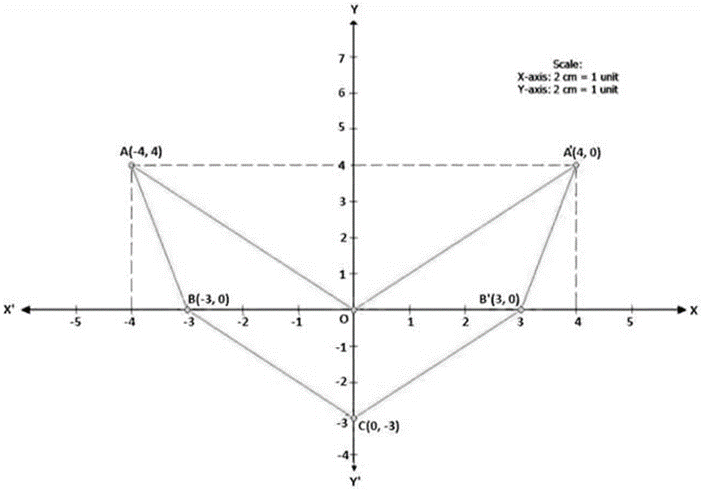
1. A’ = (4, 4) AND B’ = (3, 0)
2. The figure is an arrow head.
3. The y-axis i.e. x = 0 is the line of symmetry of figure OABCB’A’.





