Question 1. State the condition when on applying a force, the body has:
a) The translational motion
b) The rotational motion.
Solution:
a) The body creates translational motion when it is free to move.
b) The body creates rotational motion when it is pivoted at a certain location.
Question 2. Define moment of force and state its S.I unit.
Solution:
The product of the force’s magnitude and the angle at which the force’s line of action is perpendicular to the axis of rotation yields the moment of force. The S.I. moment of force unit is the Newton metre (Nm).
Question 3. State whether the moment of force is a scalar or a vector quantity.
Solution:
The moment of a force is a vector.
Question 4. State two factors affecting the turning effect of a force.
Solution:
The moment of the force about a point depends on the following two factors:
(a) The force exerted, its magnitude, and,
(b). the separation between the force’s direction of action and the axis of rotation.
Question 5. When does a body rotate? State one way to change the direction of rotation of a body given a suitable example to explain your answer
Solution:
The body rotates about the axis passing through the pivot point when the body is pivoting at a point and a force is given to the body at a suitable position. By altering the point of application of force, the direction of rotation may be varied. A disc that has been rotated at its center by moving the point of application of force F from A to B is shown in the provided figure producing. Counterclockwise and clockwise moments

Question 6. Write the expression for the moment of force about a given axis.
Solution:
Moment of force about a certain axis is = force x the perpendicular distance from the axis of rotation.
Question 7. What do you understand by the clockwise and anticlockwise moment of force? When is it taken positive?
Solution:
When a body is turned counterclockwise, the moment of force is known as an anticlockwise moment and is interpreted as positive, but when a body is turned clockwise, the moment of force is known as a clockwise moment and is seen as negative.
Question 8. State one way to reduce the movement of given force about a given axis of rotation.
Solution:
The moment of force is a function of how far the force’s line of action is from the axis of rotation. The moment of a particular force decreases as the perpendicular distance from the axis increases.
Question 9. State one way to obtain greater moment of a given force about a given axis of rotation
Solution:
A force’s moment is calculated by multiplying its magnitude by its perpendicular distance from the axis of rotation. Therefore, increasing the distance from the axis of rotation where the force would apply would be one approach to increase the moment.
Question 10. Why is it easier to open a door by applying the force at the free end of it?
Solution:
Because less force is required to spin the body, opening a door is simpler when applied at its free end. This is because the bigger the perpendicular distance, the easier it is.
Question 11. The stone of hand flour grinder is provided with a handle near its rim. Give reason.
Solution:
The handle on the manual flour mill’s stone allows for simple rotation of the stone around the iron pivot at its centre with only a slight push given to the handle.
Question 12. It is easier to turn the steering wheel of a large diameter than that of a small diameter. Given reason
Solution:
Since less force is required to turn a steering wheel with a big diameter that is located far from the centre of the rim than one with a small diameter, it is simpler to turn.
Question 13. A spanner (or wrench) has a long handle. Why?
Solution:
The long handle of a spanner (or wrench) increases the turning moment, making it easier to spin a nut with less power.
Question 14. A jack screw is provided with a long arm. Explain why?
Solution:
The extended arm of a jack screw makes raising or lowering the jack, which is used to lift a big item like a vehicle, easier.
Question 15. A, B and C are the three forces each of magnitude 4 n acting in the plane of the paper as shown in Figure. Point O lies in the same plane.
1) Which force has the least moment about O? Give a reason.
2) Which force has the greatest moment about O? Give a reason.
3) Name the forces producing (a) Clockwise (b) anticlockwise moments.
4) What is the resultant torque about the point O?

Solution:
1) We know that,
Moment of Force = Force x Perpendicular distance
Since the perpendicular distance of vector C is least from the point O.
Vector C will have the least moment about O.
2) We know that
Moment of force = Force x Perpendicular distance
Since the perpendicular distance of vector A is greatest from the point O.
Vector A will have the greatest moment about O.
3) (a) Clockwise moments will result from vectors A and B.
Explanation: If the body is rotating in a clockwise direction. The clockwise moment of force is seen as negative and is known as the moment of force.
(b) The anticlockwise moment will be produced by vector C.
Explanation: If the body is rotating counterclockwise. Anticlockwise moments of force are seen as positive moments of force.
4) Resultant torque about point O = sum of torques due to vectors A, B, and C Resultant torque about point O.
=-(4×0.9)- (4×0.8)+(4×0.6)Nm
=-3.6-3.2+2.4
=-4.4Nm
The negative sign suggests that the resultant torque is in the clockwise direction.
Question 16. The adjacent diagram shows a heavy roller, with its axle at O. which its axle at O. which is to be raised on a pavement XY by applying a minimum possible force. show by an arrow on the diagram the point of application and the direction in which the force should be applied.
Solution: diagram.
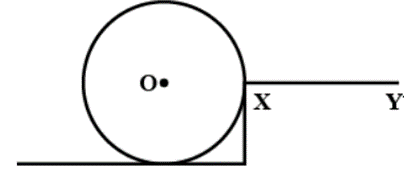
Solution: Force F should be provided in the direction as shown in the diagram.

Question 17. A body is acted upon by two force of magnitude F but in opposite direction. State the effect of the force
(i) if both forces act at the same point of the body.
(ii) if the two forces act at two different points of the body at a separation r.
Solution:
(i) Resultant force acting on the body = F – F = 0
Moment of forces = 0 i.e no motion of the body
(ii) The forces tend to rotate the body about the mid-point between two forces, Moment of forces = Fr
Question 18. Draw a neat labelled diagram to show the direction of two forces acting on a body to produce rotation in it. Also, mark the point about which rotation takes place by the letter O.
Solution:
Two equal and opposing pressures of magnitude F are applied at A and B, respectively. The bar is turned counterclockwise by the two forces.
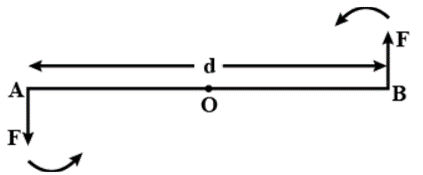
Question 19. (i) What do you understand by the term couple?
(ii) State the couple effect. Give two example of couple action in our daily life.
Solution:
(i) A pair is formed by two parallel, equal, and in opposition to one another active forces.
(ii) In order to generate the rotation, a pair is always required. For instance, twisting the steering wheel and inserting a key into a lock.
Question 20. Define moment of couple. Write its S.I unit?
Solution:
The sum of both force and the angle between the lines of action of the two forces is equal to the moment of a pair. The couple’s moment in SI is measured in Nm.
Question 21. Prove that Moment of couple = Force × couple arm.
Solution:
Two equal and opposing pressures of magnitude F are applied at A and B, respectively. The bar is turned counterclockwise by the two forces. The couple arm, ab, is the distance that separates two forces perpendicularly.
Moment of Force F at the end A=F×OA (anticlockwise)
Moment of force F at the end B=F×OB (anticlockwise)
Total moment of couple =F×OA+F×OB
=F×(OA+OB)=F×AB
=F×d (Anticlockwise)
Either force × perpendicular distance between the two forces (or couple arm)
Hence, Moment of couple = Force × Couple arm.
Question 22. What do you mean by equilibrium of a body?
Solution:
A body is said to be in equilibrium when various forces acting on it result in no change in its state of motion or rest.
Question 23. (i)State the condition when a body is in static equilibrium. Give one example of static equilibrium.
(ii) State the condition when a body is in dynamic equilibrium. Give one example of dynamic equilibrium.
Solution:
(i) A body is in static equilibrium when it continues to be in the condition of rest while being affected by the applied forces. A book on a table, for instance, is in static equilibrium.
(ii) A body is said to be in dynamic equilibrium when it maintains the same state of motion (translational or rotational) while being affected by the applied forces. A raindrop in dynamic equilibrium is one that travels to the ground at a constant speed, for instance.
Question 24. State two conditions for a body acted upon by several forces to be in equilibrium.
Solution:
For a body to be in equilibrium:
1) All forces acting on the body should result in a sum of zero.
2) All forces acting on the body around the point of rotation should have a net resultant moment of zero.
Question 25. State the principle of moments. Give one device as an application of it
Solution:
According to the principle of moments, a body is in equilibrium if the algebraic total of all the moments generated by all the forces operating on it around the axis of rotation is zero. The notion of moments governs how a physical balance (or beam balance) operates.
Question 26. Describe a simple experiment to verify the principle of moments, if you are supplied with a metre rule, a fulcrum and two springs with slotted weights.
Solution:
Using a strong thread at O as indicated; suspend a metre rule horizontally from a stable support. Now, suspend two spring balances on either side of the thread with some slotted weights W1 and W2 on them. It’s possible for the scale to slant. Keep one spring balance at position A and the other at position B while you alter the distances of the other two from the support until the scale is once again horizontal.
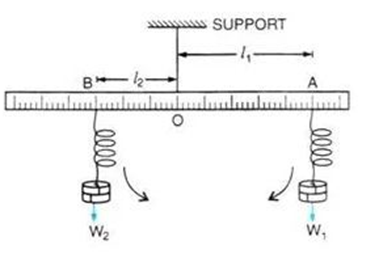
Let the weight hung from the spring balance at A on the right side of the thread be W1 at a distance of OA=l1, and the weight suspended from the spring balance at B on the left side of the thread be W2 at a distance of OB=l2.
As opposed to the weight W2, weight W1 tends to turn the scale in a clockwise direction. Clockwise moment = W1 x l1
Anticlockwise moment = W2 x l2
In equilibrium, when the scale is horizontal, it is found that
Clockwise moment = Anticlockwise moment
i.e., W1 x l1 = W2 x l2
This verifies the principle of moments.
Question 27. Complete the following sentence:
(i) The S.I. unit of moment of force is _________.
(ii) In equilibrium algebraic sum of moments of all forces about the point of rotation is ______________.
(iii) In a beam balance when the beam is balanced in a horizontal position, it is in ____________equilibrium.
(iv) The moon revolving around the earth is in ____________ equilibrium.
Solution:
(i) The S.I. unit of moment of force is newton-meter.
(ii) In equilibrium algebraic sum of moments of all forces about the point of rotation is zero.
(iii) In a beam balance when the beam is balanced in a horizontal position, it is in static equilibrium.
(iv) The moon revolves around the earth is in dynamic equilibrium.
EXERCISE-1A
MULTIPLE CHOICE TYPES
Question 1. The moment of a force about the axis depends:
a) Only on the magnitude of force
b) Only on the perpendicular distance of force from the axis
c) Neither on the force nor on the perpendicular distance of force from the axis
d) Both on the force and its perpendicular distance from the axis.
\Solution: d) Both on the force and its perpendicular distance from the axis
Question 2. A body is acted upon by two unequal forces in opposite directions, but not in the same line. The effect is that:
a) The body will have only the rotational motion
b) The body will have only the translational motion
c) The body will have neither the rotational motion nor the translational motion
d) The body will have rotational as well as translational motion.
Solution: d) The body will have rotational as well as translational motion.
EXERCISE-1A
NUMERICAL
Question 1. The moment of a force of 10 N about a fixed point O is 5 N m. Calculate the distance of the point O from the line of action of the force.
Solution:
Moment of force = force x perpendicular distance of from point O
Moment of force = F x r
5Nm = 10 x r
R = 5/10 = 0.5 m
Question 2. A nut is opened by a wrench of length 10 cm. if the least force required is 5.0 N. find the moment of force needed to turn the nut.
Solution:
Length r = 10 cm = 0.1 m
F = 5N
Moment of force = F x r = 5 x 0.1 = 0.5 Nm
Question 3. A wheel of diameter2 m is shown in the figure with the axle at O. A force F = 2 N is applied at B in the direction shown in the figure. Calculate the moment of force about Centre O and point A.
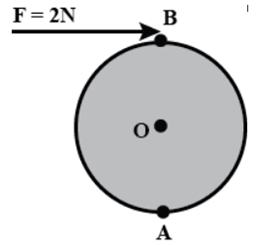
Solution:
It is given that,
F = 2N
Diameter = 2m
The perpendicular distance between B and O = 1m
1) Moment of force at point O = F x r
= 2 x 1 = 2 Nm (clockwise)
2) Moment of force at point A = F x r
= 2 x 2
= 4 Nm (clockwise)
Question 4. The diagram in the figure shows two forces F1 = 5 N and F2 = 3N acting at point A and B of a rod pivoted at a point O, such that OA = 2m and OB = 4m
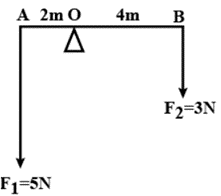
Calculate:
1) Moment of force F1 about O
2) Moment of force F2 about O
3) Total moment of the two forces about O.
Solution:
it is given that
AO = 2m
OB = 4m
1) Moment of Force F1 (= 5N) at A about the point O = F1 x OA
= 5 x 2
= 10Nm (anticlockwise)
2) Moment of force F2 = (= 3N) at B about the point O = F2 x OB
= 3 x 4
= 12 Nm (clockwise)
3) Total moment of forces about the mid-point O
= 12 – 10
= 2 Nm (clockwise)
Question 5. Two forces each of magnitude 10 N act vertically upwards and downwards respectively at the two ends of a uniform road of length 4m which is pivoted at its midpoint as shown in the figure. Determine the magnitude of the resultant moment of forces about the pivot O.

Solution:
It is given that,
AB = 4m
OA = 2m
OB = 2m
Moment of force F (=10N) at A about the point O = F x OA
= 10 x 2
= 20 Nm (clockwise)
Moment of force F (=10 N) at point B about the point O = F x OB
= 10 x 2
= 20 Nm (clockwise)
Total moment of forces about the mid-point O
= 20 + 20
= 40 Nm (clockwise)
Question 6. The figure shows two forces each of magnitude 10 N acting at points A and B at a separation of 50 cm, in opposite directions. Calculate the resultant moment of two forces about points A, B, and O, situated exactly at the middle of the two forces.

Solution:
Perpendicular distance of point A from the force F = 10 N at B is 0.5m, while it is zero from the force F = 10 N at A
Hence moment of force about A is
= 10 N × 0.5m
= 5 Nm(clockwise)
Perpendicular distance of the point B from the Force F = 10 N at A is 0.5m while it is zero from the force F = 10 N at B.
Hence moment of force about B is
= 10N × 0.5m = 5Nm (clockwise)
Perpendicular distance of point O from either of the forces F = 10N is 0.25 m
The moment if force F (=10N) at A about O
= 10N × 0.25m
= 2.5 Nm (clockwise)
And a moment of force F (=10N) at B about O
= 10 N × 0.25m
= 2.5 Nm (clockwise)
Hence total moment of the two forces about O
= 2.5 + 2.5 = 5 Nm (clockwise)
Question 7. A steering wheel of diameter 0.5 m is rotated anticlockwise by applying two forces each of magnitude 5 N. Draw a diagram to show the application of forces and calculate the moment of couple applied
Solution:
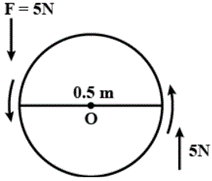
Moment of couple = either force × couple arm
Moment of couple = 5N × 0.5m
Moment of couple = 2.5 Nm
Question 8. A uniform metre rule is pivoted at its mid-point. A weight of 50 gf is suspended at one end of it. Where a weight of 100 gf should be suspended to keep the rule horizontal?
Solution:
Let us assumed that, the 50gf weight produce the anticlockwise moment about the middle point of metre rule i.e. at 50 cm.
Let us assumed that, a weight of 100gf produce a clockwise moment about the middle point. Let its distance from the middle be d cm. Then according to the principle of moments
Anticlockwise moment = Clockwise moment
=50gf×50cm
= 100gf×d

Question 9. A uniform metre rule balance horizontally on a knife-edge placed at the 58 cm mark when a weight of 20 gf is suspended from one end.
(i) Draw a diagram of the arrangement.
(ii) What is the weight of the rule?
Solution:
(i) Weight mg (W) of rule produces an anti-clockwise moment about the knife edge O. In order to balance it, 20gf must be suspended at the end B to produce the clockwise moment about the knife edge O.
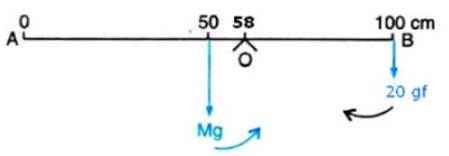
(ii) From the principle of moments,
Anticlockwise moment = Clockwise moment
W×(58-50) =20gf×(100-58)
W×8=20gf×42
W=(20gf×42)/100
W=105gf
Hence, the weight of the rule is 105gf.
Question 10. The diagram below Shows a uniform bar supported at the middle point O. A weight of 40 gf is placed at a distance of 40 cm to the left of the point O. How can you balance the bar with a weight of 80 gf?

Solution:
Anticlockwise moment = 40gf×40cm
Clockwise moment = 80gf×d cm
From the principle of moments,
Anticlockwise moment = Clockwise moment
40 gf×40cm=80gf×d
Hence, `d=(40gf×40)/80
=20cm` to the right of point O
Question 11. The figure shows a uniform metre rule placed on a function at its mid-point O and having a weight 40 gf at the 10 cm mark and a weight of 20 gf at the 9.0 cm mark.
(i) Is the metre rule in equilibrium? If not how will the rule turn?
(ii) How can the rule be brought in equilibrium by using an additional weight of 40 gf?

Solution:
(i) Anticlockwise moment = 40 gf x (50 – 10) cm
= 40 gf x 40 cm = 1600 gf x cm
The clockwise moment is not equal to the clockwise moment. Hence the metre rule is not in equilibrium and it will turn anticlockwise.
(ii) To balance it, 40gf weight should be kept on right hand side so as to produce a clockwise moment about the middle point. Let its distance from the middle be d cm. Then,
Clockwise moment= 20gf x 40cm + 40gf x d cm
From the principle of moments,
Anticlockwise moment= Clockwise moment
40gf×40cm=20gf×40+40×d cm
1600-800=40gf×d cm
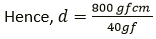
d=20cm
Hence, by placing the additional weight of 40gf at the 70cm mark the rule can be brought in equilibrium.
Question 12. When a boy weighing 20 kgf sits at one end of a 4 m long see saw, it gets depressed at this end. How can it be brought to the horizontal position by a man weighing 40 kgf?
Solution:
From the principle of moments,
Anticlockwise moment = clockwise moment
20 kgf×2 m= 40 kgf×d

Question 13. A physical balance has its arms of length 60 cm and 40 cm. What weight kept on pan of the longer arm will balance an object of weight 100 gf kept on other pan?
Solution:
From the principle of moments,
Anti-clock moment = Clockwise moment
100gf×40cm=W×60cm
Weight on the longer pan

Question 14. The diagram in the figure shows a uniform metre rule weighing 100 gf, pivoted as its center O. two weight 150 gf and 250 gf hang from point A and B respectively of the metre rule such that OA = 40 cm and OB = 20 cm . Calculate
(i) The total anticlockwise moment about o
(ii) The total clockwise moment about O
(iii) The difference of the anticlockwise and clockwise moment
(iv) The distance from O where a 100gf weight should be placed to balance the metre rule.

Solution:
(i) The total anticlockwise moment is about O
=150gf×40cm
=6000gf cm
(ii) Total clockwise moment about O,
=250 gf × 20 cm
= 5000 gf cm
(iii) The difference of anticlockwise and clockwise moment
=6000- 5000
= 1000gf cm
(iv) From the principle of moments,
Anticlockwise moment= Clockwise moment
To balance it, 100gf weight should be kept on right hand side so as to produce a clockwise moment about the O. Let its distance from the point O be d cm. Then,
150gf×40 cm=250gf × 20cm +100gf × d
6000gf cm= 5000gf cm + 100gf × d
1000gf cm=100gf×d
Hence, d=1000gfcm/100
=10cm on the right side of O.
Question 15. A uniform metre rule of weight 10gf is pivoted at its 0 mark.
(i) What moment of force depresses the rule?
(ii) How can it be made horizontal by applying a least force?
Solution:
(i) Anticlockwise moment
= 10 gf×50 cm
= 500 gf cm
(ii) From the principle of moments,
Anticlockwise moment = Clockwise moment
10 gf×50cm=W×100 cm

Question 16. A uniform half metre rule can be balanced at the 29.0 cm mark when a mass 20g is hung from its one end.
1) Draw a diagram of the arrangement.
2) Find the mass of the half metre rule.
Solution:

Figure shows a uniform half metre rule PQ which is balanced at 29 cm mark. Let M be the mass of the rule. A uniform rule has same distribution of mass throughout its length so its weight Mg will act at its middle point which is at 25 cm. The weight mg produces anticlockwise moment about point o. In order to balance the 20g (0.02kg) weight is tied at 50cm mark which generates clockwise moment.
Hence from the principle of moments
Anticlockwise moment= clockwise moment
Mg (29-25)=0.02 g (50-29)
M=21(0.02)/4
M=0.105 kg
M=105 g
Question 17. A uniform metre rule of mass 100 g is balanced on the fulcrum at mark 10 cm by suspending an unknown mass M at the mark 20 cm.
(i) Find the value of M.
(ii) To which side the rule will tilt if the mass m is moved to the mark 10cm ?
(iii) What is the resultant moment now?
(iv) How can it be balanced by another mass 50 g ?
Solution:
(i) From the principle of moments
Clockwise moment = Anticlockwise moment
100g×(50-40)cm=m×(40-20)cm
100g×10cm=m×20cm
m= 50 g
Hence, the principle moments is 50 g.
(ii) The rule will tilt on the side of mass m (anticlockwise), if the mass m is moved to the mark 10cm.
(iii) Anticlockwise moment if mass m is moved to the mark 10 cm = 50 g x (40-10) cm = 50 x 30 =1500g cm
Clockwise moment=100g x (50 – 40) cm= 1000 g cm
Resultant moment= 1500 g cm -1000 g cm= 500 g cm (anticlockwise)
(iv) From the principle of moments,
Clockwise moment= Anticlockwise moment
To balance it, 50g weight should be kept on right hand side so as to produce a clockwise moment .Let its distance from fulcrum be d cm. Then,
100g×(50-40)cm+50g×d=50g×(40-10)cm
1000g cm + 50g×d =1500g cm
50g × d=500g cm
d=10 cm
By suspending the mass 50g at the mark 50 cm, it can be balanced.
Question 18. In the following figure, a uniform bar of length l m is supported at its ends and loaded by a weight W kgf at its middle. In equilibrium, find the reactions R1 and R2 at the ends.

Solution:
According to the principle of moments,
Clockwise moments = anticlockwise moments
R1 + R2 = W
As the system is in equilibrium,
r1×1/2=r2×1/2
R1 = R2
2 R1 = W
R1 = R2 =w/2 kgf
EXERCISE-1B
Question 1. Define the term center of gravity of a body.
Solution:
The centre of gravity is the location where the total weight of the body is thought to act because the algebraic sum of the moments of weights of the constituent particles is zero around this location.
Question 2. Can the center of gravity be situated outside the material of the body? Give an example
Solution:
Yes, the centre of gravity can be located outside of the body’s physical structure. For instance, the ring’s centre of gravity.
Question 3. On what factor does the position of the centre of gravity of a body depend? Explain your answer with an example.
Solution:
The position of the centre of gravity of a body of given mass relies on its form i.e., on the distribution of mass in it. A uniform wire, for instance, has its centre of gravity at its midpoint. But if this wire is twisted into a circle, the centre of the circle will be where its centre of gravity is located.
Question 4. (i) What is the position of the centre of gravity of a rectangular lamina?
(ii) What is the position of the centre of gravity of a cylinder?
Solution:
(i) The junction of a rectangular lamina’s diagonals is where its centre of gravity is located.
(ii) The middle of the cylinder’s axis is where the centre of gravity is located.
Question 5. At which point is the centre of gravity situated in a
(i) Triangular lamina.
(ii) Circular lamina
Solution:
(i) A triangular lamina’s centre of gravity is located where its medians connect.
(ii) The centre of a circular lamina is where the centre of gravity is located.
Question 6. Where is the centre of gravity of a uniform ring situated?
Solution:
The centre of a uniform ring is where its centre of gravity is located.
Question 7. Square cardboard is suspended by passing a pin through a narrow hole at its one corner. Draw a diagram to show its rest position. In the diagram, mark the point of suspension by the letter S and the centre of gravity by the letter G.
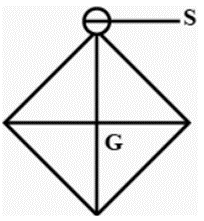
Solution:
A square cardboard object at rest, with the point of suspension at S and the centre of gravity G
Question 8. Explain how you will determine the position of the centre of gravity experimentally for a triangular lamina (or a triangular piece of cardboard).
Solution:
Take a lamina that is triangular. Make three small holes near the triangular lamina’s edge at a, b, and c. Now, suspend the provided lamina from hole “a” along with a plumb line. Make sure the lamina can freely move around the point of suspension. Draw a straight line when the lamina has come to rest along the plumb line. Repeat the experiment by suspending the lamina through holes “b” and “c,” respectively, for which we obtain straight lines to be and cf. It is seen that the lines ad, be, and cf converge to a common point G, which is the location of the triangular lamina’s centre of gravity, or the intersection of medians.

Question 9. State True or False:-
(i) The position of the centre of gravity of a body remains unchanged even when the body is deformed.
Solution: False
(ii) Centre of gravity of a freely suspended body always lies vertically below the point of suspension.
Solution: True
Question 10. A uniform flat circular rim is balanced on a sharp vertical nai by supporting it at point A, as shown in the figure. Mark the position of the centre of gravity of the rim in the diagram by the letter G.
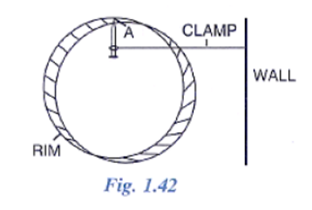
Solution:

Question 11. The figure shows three pieces of cardboard of uniform thickness cut into three different shapes. On each diagram draw two lines to indicate the position of the centre of gravity G.

Solution:
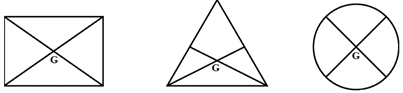
EXERCISE-1B
MULTIPLE CHOICE TYPES
Question 1. The centre of gravity of a uniform ball is
a) At its geometrical centre
b) At its bottom
c) At its topmost point
d) At any point on its surface
Solution: a) At its geometrical centre
Question 2. The centre of gravity of a hollow cone of height h is at distance x from its vertex where the value of x is:
a) h/3
b) h/4
c) 2h/3
d) 3h/4
Solution: c) 2h/3
EXERCISE-1C
Question 1. Explain the meaning of uniform circular motion. Give one example of such motion.
Solution:
A particle’s motion is referred to as being uniformly circular when it follows a circular route while moving at a constant speed. An illustration of uniform circular motion is the rotation of the earth around the sun.
Question 2. Draw a neat labelled diagram for a particle moving in a circular path with a constant speed. In you diagram show the direction of velocity at any instant.
Solution:
A particle moving in a circular path with a constant speed

Question 3. Is it possible to have an accelerated motion with a constant speed? Name such type of motion.
Solution:
Yes, a constant speed, accelerated motion exists in a uniform circular motion.
Question 4. Give an example of motion in which speed remains uniform, but the velocity changes.
Solution:
Cycling on a circular track is an example of motion where the velocity fluctuates but the speed stays constant.
Question 5. A uniform circular motion is an accelerated motion explains it. State whether the acceleration is uniform or variable? Name the force responsible to cause this acceleration. What is the direction of force at any instant? Draw diagram in support of your answer.
Solution:
When an item travels in a circle at a constant speed, its magnitude of velocity does not alter; just its continuous change in direction. It is seen as evenly accelerated motion as a result.
Question 6. Differentiate between Uniform linear motion and Uniform circular motion.
Solution:

Question 7. Name the force required for circular motion. State its direction.
Solution:
Circular motion requires a centripetal force. It is always pointed in the direction of the circle’s centre.
Question 8. What is a centripetal force?
Solution:
Centripetal force is the force exerted on a body moving in a circle. It moves in the direction of the path’s centre.
Question 9. Explain the motion of a planet around the sun in a circular path.
Solution:
A planet orbits the sun in a roughly round route, with the centripetal force required for circular motion provided by the sun’s gravitational pull on the planet.
Question 10. (i) With reference to the direction of action, how does a centripetal force differ from centrifugal force?
(ii) Is centrifugal force the force of reaction of centripetal force?
(iii) Compare the magnitudes of centripetal and centrifugal force.
Solution:
(i) They take opposing actions
(ii) The centrifugal force does not exist.
(iii) Centrifugal force refers to an object’s propensity to move away from the curve’s centre and outward when it follows a curved route. Inertia, the propensity of a thing to resist any change in its condition of rest or motion, is what causes it; it is not actually a force. A genuine force called centripetal force opposes centrifugal force and keeps an item from “shooting out,” causing it to move uniformly fast in a circular motion.

Question 11. Is centrifugal force a real force?
Solution:
No, centrifugal force is a fictitious force.
Question 12. A small pebble is placed near the periphery of a circular disc which is rotating about an axis passing through it centre.
(a) What will be your observation when you are standing outside the disc? Explain it
(b) What will be your observation when you are standing at the centre of the disc. Explain it
Solution:
(a) Observing the pebble from outside the disc reveals that it is travelling in a circular motion.
(b) When we stand in the centre of the disc, the pebble is positioned directly in front of us and is still.
Question 13. A piece of stone tied at the end of a thread is whirled in a horizontal circle. Name the force which provides the centripetal force.
a) Is the velocity of stone uniform or variable?
b) Is the acceleration of stone uniform or variable?
c) What is the direction of acceleration of stone at any instant?
d) What force does provide the centripetal force required for circular motion?
e) Name the force and its direction which acts on the hand.
Solution:
a) The speed of stones varies.
b) The stone’s acceleration varies.
c) The stone accelerates in a direction that is toward the centre of the elliptical route.
d) The centripetal force needed for circular motion is provided by the tension force in the string.
e) The movement of stress outward from the circular path’s centre.
Question 14. State two differences between the centripetal and centrifugal force
Solution:

Question 15. State True or False
(i) The earth moves around the sun with a uniform.
(ii) The motion of the moon around the earth in a circular path is an accelerated motion.
(iii) A uniform linear motion is un-accelerated, while a uniform circular motion is an accelerated motion.
(iv) In a uniform circular motion, the speed continuously changes because of the direction of motion changes.
(v) A Boy experiences a centrifugal force on his hand when he rotates a piece of stone tied at one end of a string, holding the other end in the hand.
Solution:
(i) The earth moves around the sun with a uniform. True
(ii) The motion of the moon around the earth in a circular path is an accelerated motion. True
(iii) A uniform linear motion is un-accelerated, while a uniform circular motion is an accelerated motion. True
(iv) In a uniform circular motion, the speed continuously changes because of the direction of motion changes. False
(v) A Boy experiences a centrifugal force on his hand when he rotates a piece of stone tied at one end of a string, holding the other end in the hand. False
EXERCISE-1C
MULTIPLE CHOICE TYPES
Question 1. Which of the following quantity remains constant in uniform circular motion?
a) Velocity
b) Speed
c) Acceleration
d) Both velocity and speed
Solution: b) Speed
Question 2. The centrifugal force is:
a) a real force
b) the force of reaction of centripetal force
c) a fictitious force
d) directed towards the centre of circular path
Solution: c) a fictitious force



