ICSE Class 10 Work Energy and Power Notes are one of the best materials that students can get, as it will help them to concentrate better and reduce the level of stress that students face during the furious year.
Notes are essential for conceptual understanding and scoring good marks, and for Revision, Revision Notes are always considered as the best when your exams are coming. We give ICSE Class 10 Work Energy and Power Notes in a straightforward, free downloadable PDF design for the students to figure out a better understanding of the topics.
Students should refer to Force Work And Energy ICSE Class 10 Physics notes provided below designed based on the latest syllabus and examination pattern issued by ICSE. These revision notes are really useful and will help you to learn all the important and difficult topics. These notes will also be very useful if you use them to revise just before your Physics Exams. Refer to more ICSE Class 10 Physics Notes for better preparation.
ICSE Class 10 Physics Force Work And Energy Revision Notes
Students can refer to the quick revision notes prepared for Chapter Force Work And Energy in Class 10 ICSE. These notes will be really helpful for the students giving the Physics exam in ICSE Class 10. Our teachers have prepared these concept notes based on the latest ICSE syllabus and ICSE books issued for the current academic year. Please refer to Chapter wise notes for ICSE Class 10 Physics provided on our website.
Force Work And Energy ICSE Class 10 Physics
Newton’s Second Law of Motion

Suppose a heavy wooden block is lying on a table. If we give it a gentle push, then it will move with a low velocity. In other words, if we apply a small force on the block, then its momentum will change slightly. Likewise, if we push the wooden block with a greater force, then the change in its momentum will be greater than before. We can thus conclude that the change in the momentum of a body is directly proportional to the strength of the applied force. This brings us to Newton’s second law of motion.
It is stated as follows:
The rate of change of momentum of an object is directly proportional to the unbalanced external force acting on it. The direction of the unbalanced force is
the same as the direction of the change of momentum.
Momentum and Newton’s Second Law
Consider a body of mass m. It initially moves with velocity u and accelerates at a constant rate a. It attains a final velocity v after time t. This acceleration is induced by force F.
Now, Newton’s second law of motion can be mathematically represented as follows:

Using the first equation of motion, we know that:
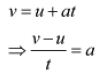
Using this, we obtain:
F = ma = Mass × Acceleration
Unit of force is taken Newton so the value of constant of proportionality (k) becomes one.
1 Newton = 1kg 1ms−2
Thus, we can restate Newton’s second law of motion as follows:
Force acting on a body is equal to the product of its mass and acceleration.
Impulse
• Impulse of a force is a measure of the total effect of the force
• Impulse = Force × Time
• Forces which act on bodies for a short time are called impulsive forces.
Example: firing a gun, hitting a ball with a bat
• It is a vector quantity.
Solved Examples
Easy
Example 1:
A moving block of mass 2 kg changes its speed from 5 m/s to 15 m/s in 2 s. Find the net force acting on the block.
Solution:
It is given that:
Initial speed (u) of the block = 5 m/s
Its final speed, v = 15 m/s
Time taken, t = 2 s
Let the acceleration due to gravity be a.
Using the first equation of motion, we know that:
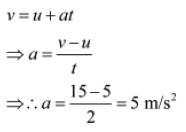
It is given that the mass of the block is 2 kg.
From Newton’s second law of motion, we know that:
F = ma = 2 × 5 = 10 N
Therefore, the net force acting on the block is 10 N.
Medium
Example 2:
A particle of mass 2 kg is subjected to a force F = kx with k = 20 N/m and x being its distance from the origin. What is its initial acceleration if it is released from a point 30 cm away from the origin?
Solution:
It is given that:
Force (F) applied on the particle = kx
Where, k = 20 N/m
x = 30 cm = 0.3 m
∴ F = 20 × 0.3 = 6 N
From Newton’s second law of motion, we know that:
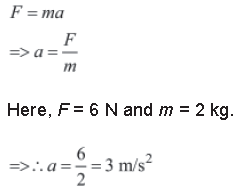
Therefore, the initial acceleration of the particle is 3 m/s2.
Hard
Example 3:
A ball of mass 150 g strikes a wall at a speed of 10 m/s and at an angle of 30°. The ball rebounds with the same speed. If the contact time is 10-3 s, then what is the force applied by the wall?
Solution:
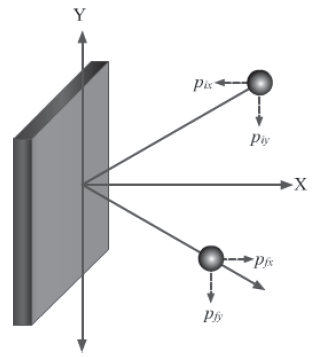
Mass (m) of the ball = 150 g = 0.15 kg
Its initial velocity, u = 10 m/s
Its initial momentum, pi = mu = 0.15 × 10 = 1.5 kg-m/s
Initial momentum of the ball along the x-axis, pix = −1.5 cos 30°
Initial momentum of the ball along the y-axis, piy = −1.5 sin 30°
Final velocity (v) of the ball = 10 m/s
Its final momentum, pf = mv = 0.15 × 10 = 1.5 kg-m/s
Final momentum of the ball along the x-axis, pfx = 1.5 cos 30°
Final momentum of the ball along the y-axis, pfy = −1.5 sin 30°
Change in the momentum of the ball along the x-axis = pfx − pix = 3cos30° = 3 × 0.866 = 2.598 kg-m/s
Change in the momentum of the ball along the y-axis = pfy − piy = 0
So, force acting along the x-axis = 2.598/103 = 2598
There is no change in the momentum along the y-axis; so, no force acts on the ball along it.
Thus, the force applied by the wall on the ball is 2598 N along the x-axis.
Did You Know?
During the free fall of a ball, the earth pulls the ball toward itself. In turn, the ball also pulls the earth upward with an equal amount of force. However, the effect of this force on the earth is negligible.
Frictional Force
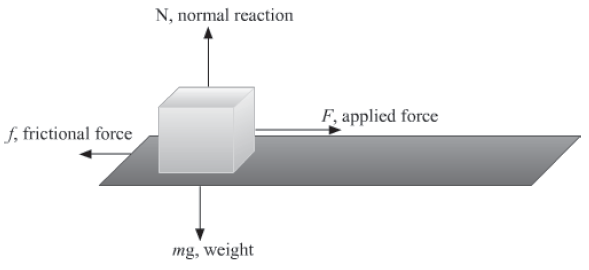
The normal reaction N is equal to the weight mg.
N = mg
The frictional force f is given by:
f = μN = μmg
Where, μ is the coefficient of friction
If the applied force is greater than the frictional force, then the acceleration a of the block is found as:
ma = F − f
=> ma = F − μmg
If the applied force just balances the frictional force, then there is no acceleration of the block and the block does not move.
So, F = f
Remember, when f is the frictional force.
Real-World Examples of Newton’s Second Law of Motion High Jump
During an athletic event, the participants in the high jump event are provided with cushions to fall on after completing a jump. This is done to prevent any kind of injury to the athletes.

When an athlete falls on the cushion, it takes her a longer period of time to come to a stop. A small stopping force acts on her because her rate of change of velocity is low.
As a result, she does not get hurt. If the athlete were to fall on a hard surface, then her velocity would reduce to zero in a very short time. In this case, a large stopping force would act on her because her rate of change of velocity would be high. As a result, the athlete would get hurt.
Seat belts

A very useful application of Newton’s second law lies in the use of seat belts in cars. To prevent injuries to passengers in case of an accident, all cars are provided with seat belts. In the event of an accident, a fast-moving car stops suddenly, i.e., its high velocity is reduced to zero in a very short interval of time. The time taken by the passengers to fall gets increased because of the seat belts worn by them. The rate of change of velocity of the passengers gets reduced because of the increase in the time taken by them to fall. Hence, a lesser stopping force acts on them, as a result of which, injuries are reduced.
Torque, Equilibrium, Principle of Moments and Centre of Gravity
When a force acts on a rigid body, two kinds of motion are exhibited.
• Linear or Translational Motion: When a rigid body, which is free to move, starts moving in a straight path along the direction of applied force, then such motion is called linear or translation motion.
• Rotational Motion: When a rigid body, pivoted at a point, starts rotating about the axis passing through the pivoted point when a force acts on it, then such motion is called rotational motion.
Torque (Moment of Force)
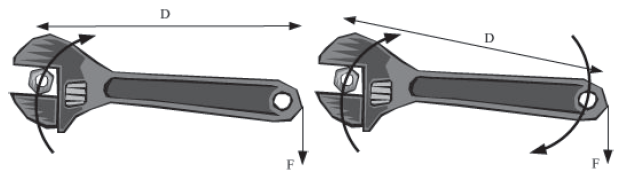
The given figure shows a wrench and a nut. When a force, F, is applied to the handle of the wrench, the nut turns in a direction as shown in the given diagram.
It is interesting to note that the greater the distance between the nut and the point of application of force (denoted by D in the figures), the easier it will be to turn the nut.
Therefore, the turning of the nut depends on two factors:
i. The greater the applied force F, the more easily the nut can be turned.
ii. The greater the distance d, the more easily the nut can be turned.
It is clear from these points that the turning effect can be increased either by increasing F or by increasing d (distance between the nut and the point of application of force F)
On account of these points, we define a quantity called torque.
Torque (τ) = Force (F) × Perpendicular distance (d)
Torque represents the turning force acting on an object. It can either be clockwise or anticlockwise, depending upon how the force is applied. The given figures show clockwise as well as anticlockwise torque.
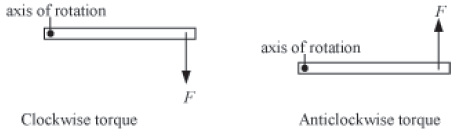
A clockwise torque tends to turn an object in the clockwise direction. Similarly, an anticlockwise torque tends to turn an object in the anticlockwise direction.
Torque is also known as moment of force.
Unit of Torque
Torque (τ) = Force (F) × Perpendicular distance (d) Since the unit of force is N and the unit of distance is m, the unit of torque is Nm (Newton-metre).
Translational Equilibrium
An object is said to be in translational equilibrium if the net force acting on the object is zero. A translational equilibrium corresponds to the state of rest or to a straight-line motion at a constant speed. It means that if an object is in translational equilibrium, the object remains at rest or continues its motion in a straight line at constant speed. The
essential condition for translational equilibrium can be given in the form of an equation as:
Σ F = 0
The given figure shows a block on which two forces are acting.

The net force on this block is 120 N − 120 N = 0 N.
Therefore, the given block is said to be in translational equilibrium.
It means that if the block is already at rest, then it will continue to be at rest after the two forces start acting simultaneously.
Also, it means that if the block was already in motion, it will continue the same type of motion after the two forces start acting simultaneously.
Rotational Equilibrium
An object is said to be in rotational equilibrium if the net torque acting on the object is zero.
Consider a drum fitted such that it can rotate around its axis. The given figures show two such drums. Arun and Pankaj tie up ropes, as shown in the given figures and pull the ropes with equal forces.
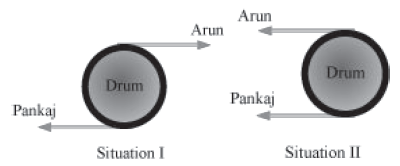
In which of the given situations will the drum not rotate? Yes, that is right! The drum will not rotate in situation II. Therefore, in situation II, the drum is in rotational equilibrium. The torque exerted by Arun is equal but opposite to the
torque exerted by Pankaj.
Clockwise and Anticlockwise Moment
Torque is also known as moment of force.
The given figure shows a metre scale that can rotate about the fixed point O.
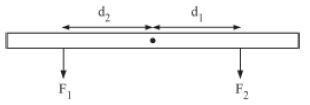
The moment of force F1 is given by:
τ1 = F1 × d1
This tends to turn the metre scale in the clockwise direction.
Hence, it is a clockwise moment.
Similarly, the moment of force F2 is given by:
τ2 = F2 × d2
It is an anti-clockwise moment. It tends to turn the metre scale in the anticlockwise direction.
For an object to remain in remain in rotational equilibrium:
Clockwise moment = Anticlockwise moment
Example
Let us consider a light rod AB of negligible mass with centre at C. Two parallel forces, each of magnitude F, are applied at the ends such that the forces are perpendicular to the rod, as shown in the figure below.
Here, total force on the rod = F − F = 0. This is because the forces act in opposite directions.
The net force on the rod is zero. Therefore, the rod is in translational equilibrium.
The moments of both forces about C are equal (= aF) but they are not opposite. They
act in the same direction and cause the anticlockwise rotation of the rod. Thus, the rod is
not in rotational equilibrium.
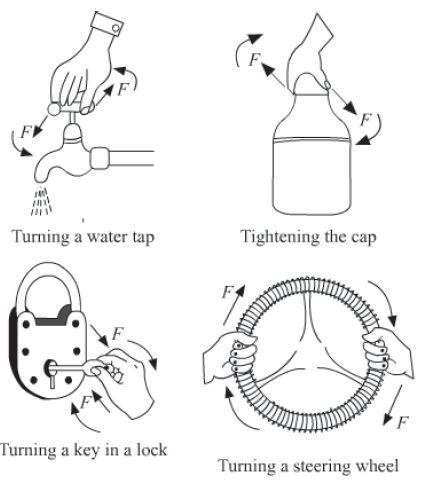
Couple
A pair of parallel forces, which are equal and opposite and are not acting along the same line, form a couple. These two equal and opposite forces always act at two different points. Such couple is always needed to produced a rotation.
Examples: Turning of a tap water, tightening the cap of a bottle, turning a steering wheel are some examples where couple is used.
Moment of Couple
It is the product of either force and perpendicular distance between the two forces or couple arm.
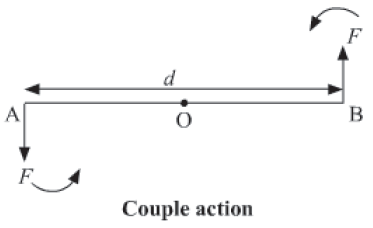
Moment of force F at the end A = OA × F (anticlockwise)
Moment of force F at the end B = OB × F (anticlockwise)
Total moment of couple = OA × F + OB ×× F = OB × F = F × d (anticlockwise)
Principle of Moments
According to the principle of moments, a body will be in rotational equilibrium if algebraic sum of the moments of all forces acting on the body about a fixed point is zero.
Example − Take an ideal lever comprising of a rod AB of negligible mass pivoted at a point O.
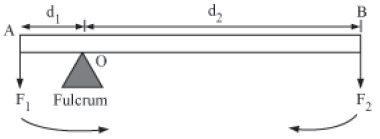
Here, F1 and F2 are two parallel forces. For translational equilibrium, net force should be equal to 0.
∴ R − F1 − F2 = 0
R = F1 + F2 … (i)
For rotational equilibrium, the algebraic sum of moments of forces about O must be zero. If AO = d1 and OB = d2, then
F1 × d1 − F2 × d2 = 0 … (ii)
From equation (ii),
F1d1 = F2d2 … (iii)
In case of the lever, force F1 is usually some weight to be lifted (called load) and its distance from the fulcrum (AO = d1) is called the load arm.
Force F2 is the effort applied to lift the load and its distance from the fulcrum (OB = d2) is called the effort arm.
From equation (iii), we have
Load × Load arm = Effort × Effort arm
The ratio F1/F2 is called mechanical advantage (M.A.) of the lever i.e.,

Usually, M.A. > 1 i.e., F1 > F2 i.e., a small effort is applied to lift a heavy load.
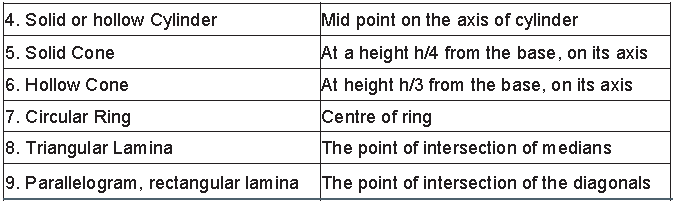
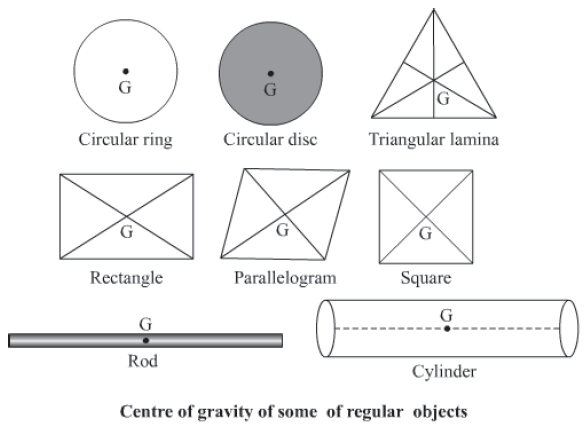
Centre of Gravity
• The centre of gravity of a body is the point at which the body’s whole weight is said to act from. The concept of centre of gravity makes it easy to do calculations for objects having extended size.
• Generally, it turns out that the centre of gravity is also the centre of mass. The centre of mass of an object is the point where the whole mass of the object is said to be concentrated.
• The Centre of gravity of a body of irregular shape can be determined by the following method.
Suspend the body from some point such as A.
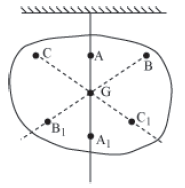
Draw the vertical line AA1. This line AA1 passes through Centre of Gravity, which lies somewhere on this line.
Similarly, draw vertical lines BB1 and CC1 by suspending the body from some other points B and C, etc. The point of intersection of these verticals gives us the position of Centre of Gravity (G) of the irregular body.
Centre of Gravity of Some Regular objects

Example
Consider the motion of a body that is rotating as well as translating, as shown in the given figure.
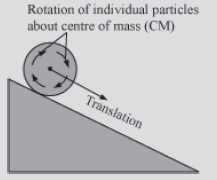
Let the mass of this irregular object be “M” and the net force acting on the object be “F”. Each of the particles of the object follow complex paths as the object is rotating as well as translating. It is, therefore, difficult to apply the equation “f = ma” on each particle. But it is possible to use this equation if the whole mass “M” of the object is considered to be concentrated at the centre of gravity of gravity (G) of the object. During the journey of the shown object, it is the point G that does not revolve. All other particles of the object revolve around the point G.
Even though it is not possible to easily track the motion of individual particles, it is possible to track the motion of point G using the equation F = Ma, where,
a is the acceleration of the centre of mass (G). Hence, the concept of centre of mass makes it easy to track the motion of an object by tracking its centre of gravity (G) with second law (F = ma) applied to this point.
Uniform Circular Motion
Uniform Circular Motion: An Overview
Circular motion is all around us. It is there in the English nursery rhyme ‘Here We Go Round the Mulberry Bush’. It is there when you go round and round an endless circle on a merry-go-round. It is there when you rotate a string with a ball tied to it. How many real-life examples of this motion can you think of in a minute? Make a list.
Now, let us learn the physics of circular motion.
Motion in a Closed Path and Circular Motion
When a body moves in a closed path, its final position is the same as its initial position. Let us consider some closed paths and an object moving on each of them at a constant speed.
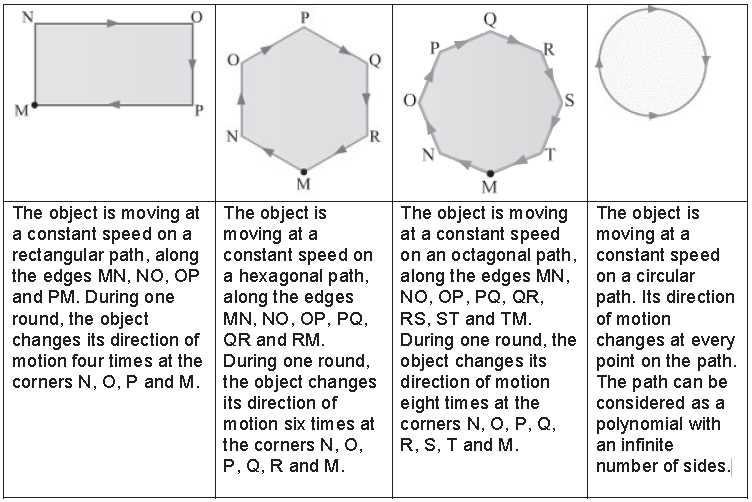
Uniform Circular Motion
When a body moves along a circular arc or a circle, it is said to be in circular motion.
What is the kind of closed path that you trace every day, right from leaving the bed in the morning to going to bed at night?
In uniform motion, the velocity of the moving body remains constant. In circular motion, the velocity can never be constant, but the speed of the moving body can be constant.
A body moving in a circular path at a constant speed is said to be in uniform circular motion.
Take a string with a ball tied at one end and rotate it. As you rotate the string, the ball traces a circular path in the air (as shown in the figure).
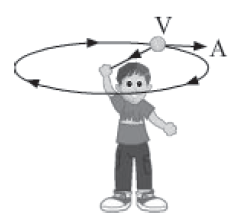
Let the length of the string be r. so, the radius of the circular track traced by the stone is r.
Let the time taken by the stone to complete one rotation be “l”.
Distance travelled in one rotation = circumference of the circular track = 2πr
Let the speed of rotation of the ball be v.
Circular Motion: Velocity at Any Instant
We know that the velocity of a body in circular motion changes at every instant. For one complete rotation, the average velocity is zero. This is because the displacement is zero. However, the body will have some finite instantaneous velocity at every instant.
The velocity of a body in a circular path is always tangential to the path and is perpendicular to the radius of the circle.
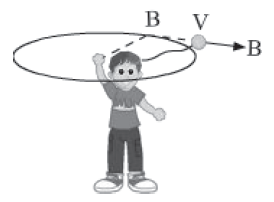
Consider once again the string with the ball tied to it. Suppose the boy loose grip of string. The stone with string will be free from boy’s hand and leave the circular path tangentially. This happens because the tension in string—provided by the centripetal force required for the revolution—vanishes when the string flies off.
Circular Motion: Velocity at Any Instant
What would happen if Earth were to stop rotating about its axis all of a sudden?
At the equator, Earth rotates about its axis at the speed of 1674.4 km/h. We cannot feel this rotation because we, too, move with Earth at the same rate. Now, if Earth were to suddenly stopped spinning, everything on its surface at the equator would suddenly move at more than 1600 km/hour tangentially. The escape velocity of Earth is around
40000 km/h, so these things would not fly off into outer space; however, the speed is high enough to project the things to about 11 km from Earth’s surface. This would result in serious damage.
When a body of mass m revolves with a uniform speed v on a circular path of radius r, the work done by the body in one complete rotation is zero. Why?
Work is the scalar product of force and displacement. In one complete rotation, the displacement is zero. So, the work done by the force is also zero.
Circular Motion: Forces
Circular motion is an accelerated motion. The velocity of a body in circular motion changes at every instant. The force that keeps the body in the circular path is called the centripetal force.
The force that acts radially inward and keeps the moving body in a circular path is called centripetal force.

The centripetal force acts on the body toward the centre. Why then does the body not leave its circular path and move toward the centre?
The answer lies in the nature of motion of the body. Circular motion is an accelerated motion. For Newton’s laws to be applicable in such motion, a fictitious force is introduced. A fictitious force is a force that doesn’t exist in reality. This force is the centrifugal force. In circular motion, the centrifugal force is always directed opposite to the centripetal force and is equivalent to the magnitude of the centripetal force. Thus, the centripetal force is balanced by the centrifugal force. This is the reason why the moon doesn’t fall down to Earth.
Centrifugal force is the fictitious outward force experienced by a body in circular path. The magnitude of this force is always equal to the centripetal force on the body and is always directed opposite to the centripetal force.
What provides the centripetal force to the moon for it to revolve around Earth?
The gravitational force of attraction between Earth and the moon provides the centripetal force required to keep the moon revolving around Earth.
Did You Know?
At the circus, the motorcyclist in the death pit or the well of death (maut ka kuan) does not fall from the wall because his high speeds along the circular path provide him with sufficient force to remain attached to the wall.
Solved Examples
Easy
Example 1:
A 150 g stone is tied at one end of a string of length 60 cm. It is made to revolve in a circular path at a constant speed. What is the centripetal acceleration of the stone if it makes two complete revolutions in a second?
Solution:

Medium
Example 2:
The radius of the nearly circular orbit of the moon around Earth is about 384000 km and the time period of revolution of the moon around Earth is 27.3 days. What is the centripetal acceleration of the moon toward Earth?
Solution:
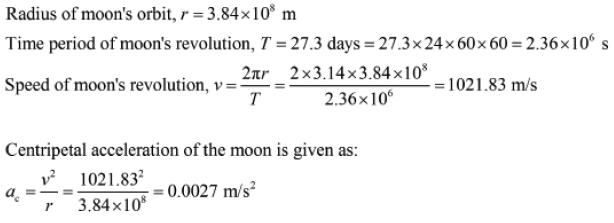
Hard
Example 3: At the circus, a motorcyclist rides in a circular track of radius r, in the vertical plane. What is the minimum velocity at the highest point of the track so that the motorcyclist can complete the track successfully?
Solution:

Centripetal and Centrifugal Forces in Nature
Do you know that Earth’s bulging out at the equator is due to the centrifugal force?
At the equator, Earth’s rotational speed is about 1674.4 km/h. The centrifugal force experienced by the land and water mass is the maximum at this region. The radially outward force experienced by the mass distribution in this region is large enough to affect Earth’s shape. This is the reason for the equatorial bulge of Earth.

Food for Thought
Take an onion and a potato. Can you think of a way to lift the potato with the onion?
Remember, the onion must be smaller than the potato.

Explanation: You will need a pen and a one-metre thread to do this activity. Take out the refill of the pen, insert the thread through one end of the pen and bring it out from its other end. Each end of the thread must be at least 30 cm from the pen. Attach the onion to one end of the thread and the potato to the other. Now, rotate the pen such that the
onion starts revolving about it. The potato rises as you increase the speed of revolution of the onion.
The centripetal force required to move the onion in the circular path is provided by the tension in the thread, which is in turn induced by the gravitational force on the potato. When the speed of revolution of the onion is increased, the centripetal force necessary for this motion also increases. When the tension in the thread exceeds the weight of the
potato, the potato rises.
Decreasing the speed of revolution decreases the centripetal force and, consequently, makes the potato go down.
Work
Work − Basic Idea
In everyday usage, the word ‘work’ indicates any activity involving physical or mental effort aimed at achieving some definite and well-defined objective. In contrast, the scientific usage of this term has a more restricted meaning.
In science work is said to be done by a force when a force causes a displacement of a body. Thus, work in scientific term is dependent on the force applied and the displacement caused. Since, force and displacement are vector quantities we must consider the angle between the force and displacement also.
Scientifically, no work is done in any of the preceding examples. This is because there is no net displacement of any object.
Work − Definition and Unit
In physics, the term ‘work’ is used to define situations where motion results through the action of a force. The amount of work done is measured by multiplying the applied force with the distance through which a body moves along the line of action of the force.
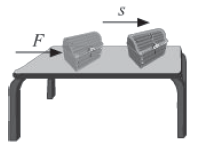
Suppose a wooden box is kept on a table. When a force of magnitude F acts on the box, it gets displaced through a distance s in the direction of the applied force (as shown in the figure).
Thus work done (W) is given by the scalar product of force (F) and displacement (s).
Work = Force × Displacement
W = F x s
So, work can be defined as follows:
The work done in moving a body is equal to the product of the force on the body and the displacement of the body in the direction of the applied force.
The SI unit of work is joule (J).
When a body moves a distance of one metre along the direction of an applied force of one newton, the work done is one joule.
J = 1 N × 1 m = 1 N-m
Did You Know?
Work is the product of force and displacement. Both force and displacement have agnitude as well as direction. However, work has only magnitude, and no direction.
This is because work is the scalar product of two vectors—force and displacement.
Since force and displacement are vector quantities, we must consider the angle between them as well.
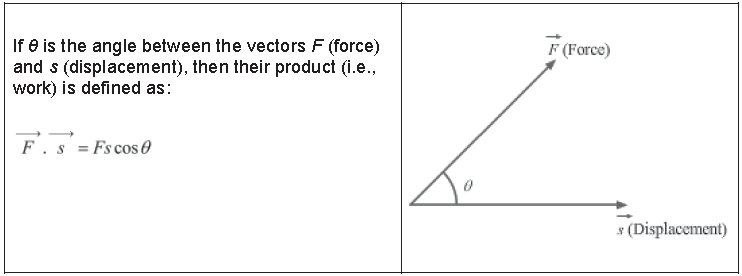
The product of F and s is a dot product. Dot products are scalar in nature, i.e., they have magnitude, but no specified direction.
Solved Examples
Easy
Example 1:
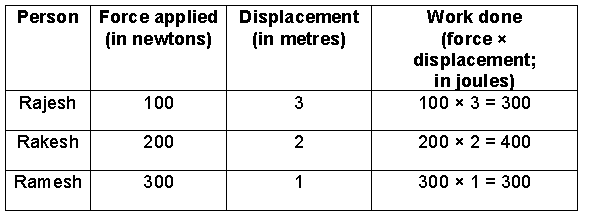
Rajesh, Rakesh and Ramesh push a heavy box one by one along the ground. The following table lists the magnitude of force applied and the displacement of the box in each case.
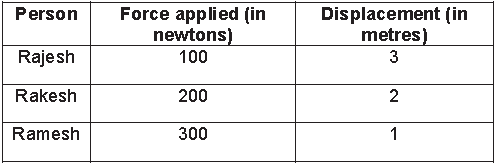
Who has done the maximum amount of work on the box?
Solution:
The following table shows the amount of work done on the box by each person. It is clear that Rakesh has done the maximum amount of work.
Medium
Example 2a:
What is the force acting on a body displaced through a distance of 100 hectometres due to work of 500 erg?
Solution:
Work = 500 erg = 5 × 10−5 J
Displacement = 100 hm = 104 m
We know that:
Work = Force × Displacement
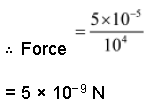
Example 2b:
A force of 2.5 N is acting on an object, causing the object to be displaced by 1.8 metres in the direction of the force. What is the work done by the force?
Solution:
We know that:
Work done = Force × Displacement
Applied force = 2.5 N
Displacement = 1.8 m
∴ Work done = 2.5 × 1.8 = 4.5 J
Hard
Example 3a:
Consider the three scenarios.
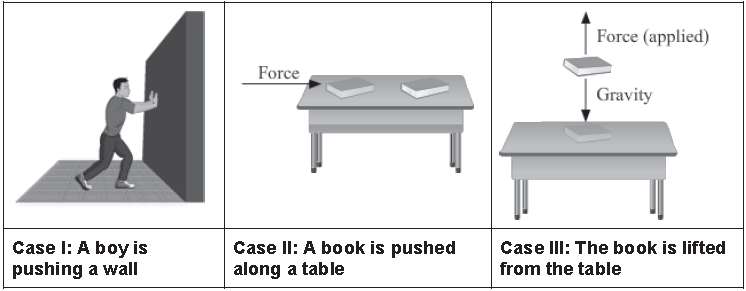
In which of the above case(s) is work done?
Solution:
Work is done in ‘Case II’ and ‘Case III’.
Case I: Even if we push a wall with the maximum force that we can apply, the wall will not move. Thus, there is no net displacement, and consequently, no work is done.
Case II: If we push a book along a table, then it will move to a certain distance depending upon the force applied. Thus, there is a net displacement in the position of the book, and consequently, work is done. This work is done against the frictional force existing between the book and the surface of the table.
Case III: If the book is lifted to a certain height, then a force is exerted against gravity. This force displaces the book to the said height. Thus, once again, there is a net displacement in the position of the book, and consequently, work is done.
Example 3b:
A satellite of mass 2000 kg is revolving around the earth in a nearly circular orbit of radius 42000 km. The gravitational force of attraction between the earth and the satellite is 450 N.
What is the work done by the earth on the satellite?
Solution:
Scientifically, work done by a body is considered to be equal to zero when the direction of force and that of displacement are at right angle with each other. Hence, the displacement in the direction of applied force is zero that ultimately makes the work done zero.
In the given case, the satellite is moving around the earth in a nearly circular orbit. Therefore, its direction of displacement at any instant will be perpendicular to its orbit. And hence, the gravitational force of earth will act at right angle to the direction of motion of satellite. This is also shown in the following figure.
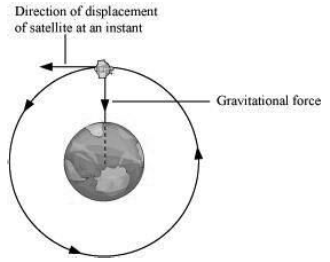
Therefore, the work done by the earth on the satellite moving around it is zero.
Know Your Scientist
James Prescott Joule (1818−1889)

He was an English physicist. At the age of sixteen, he studied with the British chemist, John Dalton. He began his independent research in a laboratory built at home where he hoped to replace steam engines with electric motors. He was also an inventor. He invented electrical welding and the displacement pump. The unit of energy is named in his honour.
Work Done by a Constant Force
Positive Work
A force is said to do work when it induces a displacement. If the force and displacement are in the same direction, then the work done is positive. If the force and displacement are in opposite directions, then the work done is negative.
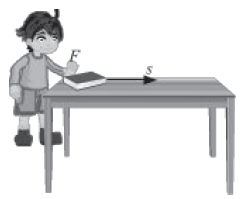
Positive work: A book being pushed along a table If force and displacement are in the same direction, then the angle between them is 0o.
We know that:
Work done (W) = Force (F) × Displacement (s) × cos θ
So, we get:
W = F × s × cos 0°
= Fs ( cos 0° = 1)
Negative Work

Negative work: A soccer player’s hand pushed backward while stopping a fast-moving football
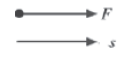
If force and displacement are in opposite directions, then the angle between them is
180°.
So, we get:
W = F × s × cos 180°
= −Fs∴( cos 180° = −1)
Zero Work
Zero Work
The following table lists the conditions for zero work done.



While the coolie moves forward, he exerts a net force in the upward direction. The force and displacement are perpendicular to each other. Hence, the work done is zero, as is shown by the calculation below.
W = F × s × cos θ
= F × s × cos 90°
= F × s × 0 = 0
No work is done by a coolie when he walks with a heavy luggage on his head.
Zero Work- Examples
Take a look at these examples of the three conditions for zero work.
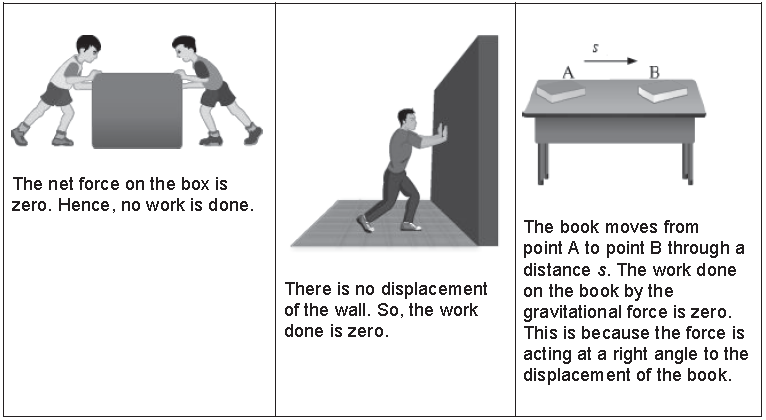
Work Done Against Gravity
The force of gravity acts on all objects bound to Earth. Any object on Earth’s surface experiences a gravitational pull—called weight—towards Earth’s centre. If an object is to be displaced in the upward direction, then work has to be done against this gravitational pull.
Suppose a block of mass m is on Earth’s surface. The weight of the block is mg. This weight acts vertically downward. At the same time, the ground also exerts an equal and opposite force—as a reaction force—on the block. As a result, the block remains at rest. Let us now apply a force F, which is slightly larger than the weight of the block, in the
upward direction.
F ≈ mg
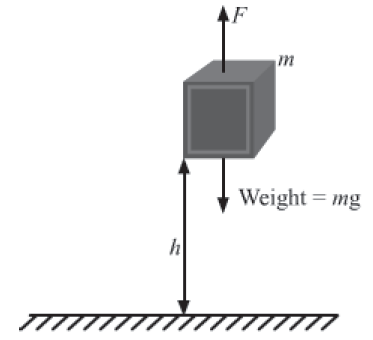
As the block leaves the ground, this applied force moves it in the upward direction with zero acceleration. The acceleration is zero because the applied force is negligibly larger than the weight of the block.
The block is moved to a height h above the ground. Thus, the applied force causes a displacement h of the block in the upward direction.
The force and displacement are in the same direction. It is essential that the height h is very small compared to Earth’s radius.
So, the work done by the applied force in moving the block against gravity with zero acceleration is given as:
W = F × h = mgh
Work Done by a Force Acting Obliquely to Displacement
A force making an angle with the motion of an object will not completely take part in inducing the motion of that object. Only the component of the force along the direction of displacement will be responsible for the motion of the object.
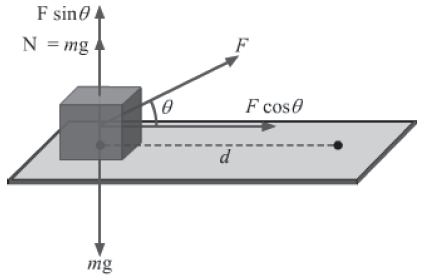
Suppose force F is acting on a block of mass m and is making an angle θ with the horizontal.
This force can be resolved into two perpendicular components.
• The horizontal component of the force is given as: F cos θ
• The vertical component of the force is given as: F sin θ
Net vertical force = Normal reaction due to the floor + Vertical component of the force = N + F sin θ
It is the horizontal component of the force which causes the displacement s of the block. So, the work done on the block by the force F is given as:
W = (F cos θ) s = Fs cos θ
Solved Examples
Easy
Example 1:
How much work is done by the gravitational force when 256 kg block of wood falls through 2.80 m?
Solution:
Force with which the block of wood is pulled down by gravity is, F = mg = (256)(9.8) = 2508.8 N
The force and the displacement are both downwards, so the angle between them is 0o.
So, work done is, W = Fd = (2508.8)(2.80) = 7024.64 J
Medium
Example 2:
The work done in lifting a suitcase from the floor to a table depends on
a. the path you take to lift the suitcase
b. the time you take to lift the book
c. the height of the table from the floor
d. the mass of the suitcase and hence its weight
Solution:
The work done in lifting a suitcase is equal to the change in PE of the suitcase. It is
equal to the product of the weight of suitcase and the height of the table.
(a) Work does NOT depend on the path, as long as there are no non-conservative forces doing work.
(b) Work does NOT depend on the time taken.
(c) Work DOES depend on the height of the table − the higher the table, the more work it takes to lift the suitcase.
(d) Work DOES depend on the weight of the suitcase − the more the suitcase weighs the more work it takes to lift the
suitcase.
Hard
Example 3:
A force of 10 N acting on a body of mass 2 kg, which was initially at rest, at an angle of 600 with the horizontal direction displaces the body through a distance of 2 m along the surface of a floor. Calculate the work done and the kinetic energy of the block.
Solution:
Force, F = 10 N
Angle with horizontal, θ = 60o
Displacement in horizontal direction, S = 2 m
Component of force along horizontal direction is = F cosθ = (10)(cos60) = 5 N
So, work done is, W = (5)(2) = 10 J
The acceleration of the block is, a = F/m = 10/2 = 5 m/s2
Using,
v2 = u2 + 2as
=> v2 = 0 + (2)(5)(2) = 20
=> ½ mv2 = (0.5)(2)(20) = 20 J
Energy
Work and energy are the two terms used very often in our day-to-day lives. We often call someone very energetic, if the person is capable of doing a lot of work. In physics also, energy and work are very closely related and their meanings are not very different from the way we use them in our daily lives. What is the relation between work and
energy?
Energy is defined as the ability to do work.
You know what work is.
When a force displaces an object along its direction, we say the force does a work.
Therefore, a body has the ability to do work, if it possesses some energy. Without spending energy, a body cannot do any work. If we think about it a bit, then we will see that to apply a force, some amount of energy has to be spent. From this, we can also conclude that if work is done on a body, then some energy gets transferred to the body.
For example, if we lift a stone to a certain height, then a work is done on the stone to lift it against the force of gravity. For that, we use energy stored in our muscles. Again, the work is stored as energy in the stone by virtue of its position. Therefore, when the stone is released from the height, the stored energy gets released.
Thus, we can conclude that energy is required to do some work. On the other hand, if some work is done on a body, then the spent energy that gets stored in the body in turn becomes capable to do some work. This is called work−energy relation.
Power
Here, the tortoise and rabbit apply the same force to move the box through the same distance. The rabbit gets lazy, but the tortoise maintains its slow and steady pace. Undoubtedly, both do the same work, but the tortoise takes less time to complete the work. So, the tortoise proves to be more powerful.
Considering that the same force of magnitude is applied, the work done to raise a weight through a distance is the same as the work done to push another weight through the same distance. The time required to do the work determines the rate of working, but has nothing to do with the amount of work.
Power − Definition and Unit
A given amount of work may be done either in a short time or a long time. In commercial operations, the rate of working or the work done per second/per hour is an important consideration.
Power is defined as the rate of doing work. The SI unit of power is watt (W) which is joules per second.
This relation shows that for a given work, power is inversely proportional to the time taken. We can obtain a mathematical relation for power by dividing the work done by time taken.

We know that energy is consumed when work is done. Therefore, we can also define power as the rate at which energy is consumed or utilised. Consequently, we can calculate power by dividing energy consumed by time taken.

Since energy has only magnitude and no direction, power also has only magnitude and no direction.
Power is also defined as the product of force and average speed.
If a constant force F acts on a body and displaces it by distance S in the direction of force in time t, then
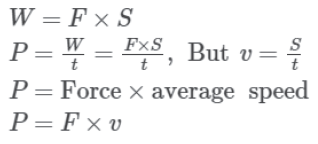

Know Your Scientist
James Watt (1736−1819)
He was a Scottish inventor and mechanical engineer. Improving upon the Newcomen steam engine, he developed his own machine. Used for pumping water out from mines, it was four times more powerful than other machines based on Thomas Newcomen’s design. Watt measured the power of his steam engine with a strong horse. This led him to conclude that a ‘horsepower’ equals 746 watts.
Know Your Scientist
Power − Definition and Unit
1 Watt is the power of a device that does work at the rate of 1 joule per second. We can also say that power is 1 W when the rate of consumption of energy is 1 Js- 1. We express larger rates of energy transfer in terms of kilowatt (kW), with 1 kW = 1000 W.
Horse power: It is another unit of power, broadly used in mechanical engineering. 1 H.P. = 746 W = 0.746 kW
Solved Examples
Easy
Example 1:
A body does hundred joules of work in ten seconds. What is its power?
Solution:
Power can be calculated as follows:
Power = Work done / Time takes
Here, work done = 100 J
Time taken = 10 s
On putting these values in the formula, we get:
Power = 100 J / 10 s = 10W
Hence, the power of the body is ten watts.
Medium
Example 2:
A pump lifts ten kilograms of water in two seconds to the top floor of a house from the ground. The height of the house is ten metres. What is the power of the
pump?
(Take g = 9.8 m/s2)
Solution:
First, we need to calculate the work done by the pump in lifting water against the force of gravity.
The work done against gravity is given as:
Hence, the power of the pump is 490 W.
W = mgh
Here, mass (m) of the water lifted = 10 kg
Acceleration due to gravity, = 9.8 m/s2
Height (h) of the house = 10 m
Therefore the work done by the pump gravity is :
W = 10 x 9.8 x 10 = 980 j
Time takes (f) to lift the water = 2s
Hard
Example 3:
Water is to be pumped to fill a tank of volume 30 kL at a height 40 m from the ground in 15 minutes by a water pump on the ground floor. What is the electric power consumed by the water pump? Efficiency of the pump is 30%. Density of water is ρ = 1000 kg/m3 and g = 9.8 m/s2.
Solution:
Volume of water pumped up in the 15 min is = 30 kL = 30 m3
So, mass of water pumped = Vρ = 30ρ kg
Weight of water pumped = 30ρg N
So, work done in pumping water to a height 40 m above ground = weight × height
= (30ρg)(40)
= 1200ρg
So, power required to lift this water in 15 min or 900 s is = 1200ρg/900 = 4ρg/3 Let, P be the power consumed by the pump. 30% of this power is only used to lift the water.
So, 30% of P = 4ρg/3
=> 0.30P = 4(1000)(9.8)/3
=> P = 43555.5 W
Kinetic Energy
Energy
The world requires a lot of energy. To satisfy this demand, we have natural energy sources such as the sun, wind, water at a height and tides. We also have artificial energy sources such as petroleum and natural gas.

Energy exists in various forms. Some of these are
• Light energy
• Sound energy
• Heat energy
• Mechanical energy
• Electrical energy
• Chemical energy
• Nuclear energy
Kinetic Energy
Mechanical energy is the energy possessed by an object having the potential to do work. It is associated with the motion or the position and configuration of the object. Mechanical energy is of the following two types.
• Kinetic energy (associated with the motion of an object)
• Potential energy (associated with the position and configuration of an object)
The amount of energy carried by a moving object is linked to its mass and speed. This energy is called kinetic energy. For example, a moving truck causes more damage than a small car travelling at the same speed. which implies that the truck carries more energy than the car.
Kinetic Energy
The energy of a body by virtue of its motion is called kinetic energy.
The SI unit of work is joule (J), named after the physicist James P. Joule.
Suppose a body of mass m is moving with a uniform velocity u. Let an external force be applied on it so that it gets displaced by distance s and its velocity becomes v. In this scenario, the kinetic energy of the moving body is equal to the work that was required to change its velocity from u to v.
Thus, we have the velocity−position relation as:
v2 = u2 + 2as
OR
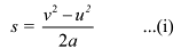
Where, a is the acceleration of the body during the change in its velocity Now, the work done on the body by the external force is given by:
W = F × s
F = ma …(ii)
From equations (i) and (ii), we obtain:
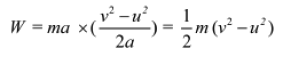
If the body was initially at rest (i.e., u = 0), then:
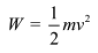
Since kinetic energy is equal to the work done on the body to change its velocity from 0 to v, we obtain:
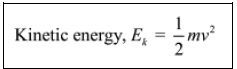
The kinetic energy of a body is directly proportional to —
• Its mass (m)
• The square of its velocity (v2)
It is the kinetic energy of the wind that is used for generating electricity through windmills.
Relationship between kinetic energy and momentum
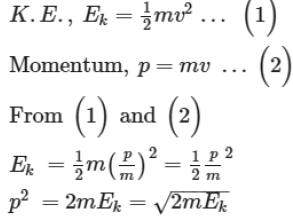
Work−Energy Theorem
Work can be done to induce motion in a body at rest. The moving body possesses kinetic energy. Thus, we can say that the work done on the body is stored in it as some form of energy.
The work−energy theorem states that the work done on a body is equal to the change in the kinetic energy of the body.
Suppose a body of mass m pushed by a force F has an acceleration a, due to which its velocity is u at time t = t1 and its velocity becomes v at time t = t2.
The force on the body is, F = ma
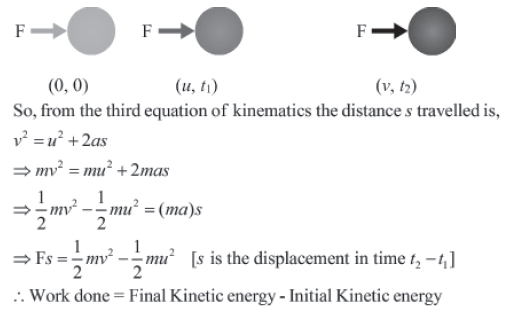
Thus, the work done by the force to increase the speed of the moving body is stored in the body as its increased kinetic energy.
Potential Energy
Potential Energy: Core Concepts
An object possesses potential energy by virtue of its position or height.
Take a rubber band and stretch it. When you release one end of the rubber band, it returns to its original position. The band had acquired energy in the stretched position. How did it acquire this energy?
Take a spring-loaded toy car and wind it using its key. When you release it on the ground, the toy car begins to move. How did it get this energy to move?
In the above case, the energy was stored in the objects because of the deformations in their configuration. When work was done to change their shape, energy got stored in them. This energy is also known as potential energy or elastic potential energy.
So, when you stretched the rubber band, you transferred energy to the rubber band. Similarly, when you wound the spring of the toy car, you transferred energy to the spring. Consequently, the rubber band and the spring retained potential energy by virtue of their configuration.
We can thus define potential energy as the energy stored in a body by virtue of its position or configuration.
Potential Energy of an Object at a Height
As the distance or height of a body from the ground changes, the potential energy possessed by the body also undergoes change. As it rises, its potential energy also increases. Its potential energy becomes zero when it is brought back to the ground level.
Suppose a body of mass m is initially at a height h1 from the ground. It is then taken to a height h2.
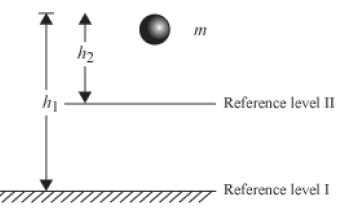
Note: Gravitational potential energy depends upon the reference level
Potential energy at height h1 = mgh1
Potential energy at height h2 = mgh2
Change in potential energy due to change in height = mg (h2 − h1)
Let us say that the body was originally on the ground and was then taken to a height h. In that case,
h1 = 0
h2 = h
So, change in potential energy = mg (h2 − h1) = mg (h − 0) = mgh
Whiz Kid
The potential energy of an object at a height depends upon a chosen reference level, called the zero level. It is so named because the potential energy of an object placed on this reference level is zero. In the given figure, the potential energy of the ball with respect to ‘Reference level I’ is greater than the energy it possesses with respect to
‘Reference level II’.
Solved Examples
Easy
Example 1:
What is the potential energy of a body of mass 2 kg kept at a height of 10 m above the zero level? (Take g = 9.8 m/s2)
Solution:
The potential energy of the body is computed as:
Ep = m × g × h
Here, mass, m = 2 kg
Acceleration due to gravity, g = 9.8 m/s2
Height, h = 10 m
∴ Ep = 2 × 9.8 × 10 = 196 J
Hence, the potential energy of the body is 196 J.
Medium
Example 2:
The potential energy of an object of mass 10 kg increases by 5000 J when it is raised through a height h. What is the value of h? (Take g = 9.8 m/s2)
Solution:
The potential energy of the object is given as:
Ep = m × g × h
Here, mass, m = 10 kg
Acceleration due to gravity, g = 9.8 m/s2
Potential energy, Ep = 5000 J
⇒ 5000 = 10 × 9.8 × h
⇒ ∴ h = 5000/98 = 51.02 m
Hard
Example 3:
‘n’ books each of thickness ‘d’ and mass ‘m’ lie flat on a table. How much work is required to stack them one on top of another?
Solution:
No work is done to place the first book as it is already in position.
The second book must be moved upwards by a distance d and the force required is equal to its weight, mg.
The force and the displacement are in the same direction, so the work is mgd.
The third book will need to be moved a distance of 2d by the same size force, so the work is 2mgd.
Similarly, the work done to lift the nth book is (n – 1) mgd.
Thus the work done is, W = mgd + 2mgd + 3mgd +…………… + (n – 1)mgd
=> W = ½ n(n − 1)mgd
Potential Energy and Work
Work has to be done to raise the potential energy of a body. The work done in changing the position or configuration of a body is stored in the body as potential energy.
Suppose a body of mass m is initially at a height h1 from the ground. It is then taken to a height h2. A force equal to its weight, mg, is applied to increase its height and the body is moved with zero acceleration.
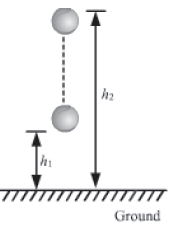
The work done by the force mg in displacing the body from height h1 to height h2 is given as:
W = mg (h2 − h1)
This expression is the same as the change in the potential energy of the body. Thus, we can say that the work done in changing its height is stored in it as potential energy.
Energy Stored in a Compressed Spring
Suppose a spring of spring constant k is compressed by a length x.
The work done in compressing the spring is found to be:
This work done is stored in the spring as elastic potential energy.
∴ Elastic potential energy of a spring compressed by a length x = 1/2kx2
Law of Conservation of Energy
Conservation of Energy − An Overview
The energy that you use to press the enter/return key on your keyboard has its source in the sun. Strange, isn’t it? The red light at the bottom of the computer mouse glows using electrical energy generated in a thermal or hydel power station. In a power station, different forms of energy get converted into electrical energy for our use.
Nowhere in this universe is energy ever created. It is only converted from one form to another. Go through this lesson to understand the concept behind the law of conservation of energy.
Consider a system of bodies which neither receives energy from without nor gives up any. In such a system, the total amount of energy remains unchanged—regardless of the actions or changes that may take place within the system. This unchanging energy simply manifests itself in different forms (e.g., sound, heat, light, etc.). Our universe is such a system of bodies.
The law of conservation of energy states that the total energy of this universe is conserved or constant. Energy cannot be created or destroyed; however, it can be transformed from one form to another.
The sum of the kinetic energy and potential energy of a system is called mechanical energy.
EMech = Kinetic energy + Potential Energy Or, EMech = K + U
These two forms of energy change as they transform back and forth into each other; however, at any point, their sum remains constant.
ΔEMech = ΔK + ΔU
The mechanical energy of a system is conserved only when the system does not gain or lose energy in any form.
Quick Questions
Question 1: So many forms of energy are observed in nature. How do we use these forms of energy in our daily life? The chemical energy stored in an electric cell can be used to power a bulb to produce light. Where does this light energy come from?
Solution: Various devices like generators, wind mill, solar panel etc convert one form of energy to another. Example: Wind mill converts wind energy to electrical energy which can be used to light a bulb or charge batteries.
In an electric cell the chemical energy gets converted into electrical energy which heats the filament of a bulb. The hot filament produces light and some heat. Thus, we have chemical energy transformed into heat and light energy.
Question 2: How the transformation of energy takes place in the wind-up toy car? What is the prime source of energy in the process? Do you know any more toys that work on the same principle?
Solution: When you turn the key of the wind-up toy car the muscular energy from your body is stored in the coiled spring of the toy car. Which when released rotates the wheel of the toy car and hence the energy appears as the kinetic energy of the car.
The energy of the muscle comes from the food we take which is obtained from plants and animals. The prime source of the energy contained in the food molecules comes from the sun. Thus, sun is the prime source of energy in the process.
Total energy of a freely falling body is always constant. Let see this using a graphical representation.

A body of mass m is falling freely under the action of gravity from the height h above the ground. As this body falls down, its potential energy changes into the kinetic energy but at each point of motion the sum of potential and kinetic energy remains unchanged. Hence the mechanical energy remains conserved.
Curve Showing Conservation of Mechanical Energy of a Freely Falling Body:
Similarly, when a body is thrown up with some initial velocity, its kinetic energy goes on decreasing whereas its potential energy goes on increasing with height. The motion is such that at each point of time mechanical energy remains conserved.
Thus, the initial kinetic energy of the body of mass m thrown upwards with say initial velocity u to reach certain height, say h, must be equal to the potential energy of the body at that height. So,
Conservation of Mechanical Energy in a Simple Pendulum
A simple pendulum consists of a bob suspended from a string with a support. It works on the principle of alternative transformation of kinetic and potential energy. At any instant, the total energy of the bob remains the same.
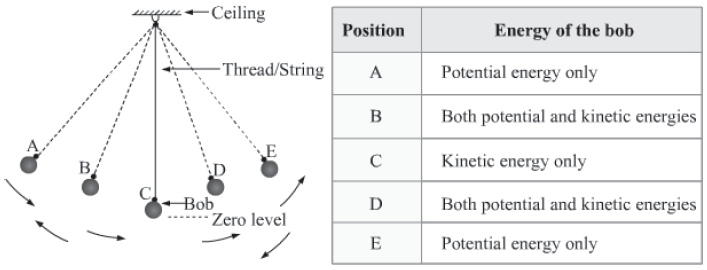
At point A, the bob has potential energy, but zero kinetic energy. This is because it is at rest. When released from this point, its potential energy starts decreasing. At the same time, it gains kinetic energy. Consequently, at point B, it has both potential and kinetic energy.
Potential energy becomes zero as the bob passes through the zero level at point C. As it moves further, its kinetic energy starts decreasing. Simultaneously, it gains potential energy. Thus, at point D, the bob has both forms of energy. Finally, at point E, the bob is again at rest and has only potential energy (like when it was at point A).
Solved Examples
Easy
Example 1:
Two bodies of masses 6m and 12m are kept at a height of h and 2h from a reference level. What is the ratio of potential energy of the masses?
Solution:
Mass of A is 6m
Height of A from the ground is h
PE of A is = (6m)(g)(h) = 6mgh
Mass of B is 12m
Height of A from the ground is 2h
PE of A is = (12m)(g)(2h) = 24mgh
Therefore,
PE of A : PE of B = 6mgh : 24mgh = 1 : 4
Medium
Example 2:
A ball of mass 200 g is dropped from a height of 10 m. What will be its velocity
when it hits the ground? (Take g = 9.8 m/s2)
Solution:
By the law of conservation of energy:
Loss in the potential energy of the ball = Gain in the kinetic energy of the ball
Loss in potential energy = mgh
Here, m = Mass of the ball = 200 g
g = Acceleration due to gravity = 9.8 m/s2
h = Height from which the ball falls = 10 m
Gain in kinetic energy = 1/2 mv2
Here, v = Velocity of the ball just before it hits the ground
According to the law of conservation of energy:
mgh = 1/2 mv2
⇒ v2 = 2gh
⇒ v2 = 2 × 9.8 × 10 = 196 (m/s)2
⇒ v = 14 m/s
Therefore, when the ball hits the ground, its velocity will be 14 m/s.
Hard
Example 3:
Two objects of masses m1 and m2 have same kinetic energy. Both are stopped with the same retarding force F. If m1 > m2, then which mass will stop in shorter distance?
Solution:

Different Forms of Energy and Its Transformation (Energy Chain)
You must have heard of energy drinks. What are the drinks meant for? They are supposed to provide you more energy so that you can do more work. Thus, you can easily conclude that energy and work are related to each other. The ability to do work is called energy.
The world requires a lot of energy. To satisfy this demand, we have natural energy sources such as the sun, wind, water at a height, tides, etc. We also have other energy sources such as petroleum, natural gas, etc.

Energy exists in various forms such as light, sound, motion, etc.
Forms of energy
Some forms of energy are:
• Mechanical
• Light
• Heat
• Muscular
• Sound
• Magnetic
• Electrical
• Chemical
• Nuclear
In this section, we will consider only mechanical energy.
Mechanical energy
It is the form of energy possessed by an object that has the potential to do work. It is caused by the motion or the position and configuration of the object. Mechanical energy is of two types:
• Kinetic energy (caused by motion of the object)
• Potential energy (caused by position and configuration of the object)
Kinetic energy
A body possesses kinetic energy by virtue of its motion. A moving arrow can be embedded into an object. Hence, it is said that the arrow possesses kinetic energy.
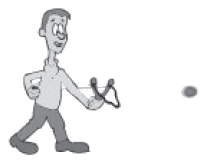
The elastic string of a catapult is stretched to throw a stone. The work done is stored in the stone and the string. After its release, the stone is said to possess kinetic energy.
Kinetic energy of a body can be calculated using the expression,
K.E. = 1/2 mv2
(where, m= mass and v2= the square of its velocity)
Its SI unit is Joule (J).
From the above formula it is clear that kinetic energy of a body increases with its velocity. Kinetic energy of a body is directly proportional to
(i) its mass (m) and
(ii) the square of its velocity (v2)
It is the kinetic energy of the wind that is used in windmills to generate electricity.

Potential Energy
Therefore, you have learned that
• potential energy possessed by a body by virtue of its configuration is known as elastic potential energy
• potential energy possessed by a body by virtue of its position with respect to the ground is known as gravitational potential energy Potential energy of a body can be calculated using the expression,
P.E. = mgh
(where, m= mass, g= acceleration due to gravity, and h= height)
The SI unit of potential energy is Joule.
A body possesses potential energy by virtue of its configuration or position.
Where does a keyed toy car derive energy to move?
Take a rubber ball and go to the top floor of your house. Now, drop the ball from a height on the floor on which you are standing. The ball will be rebound to some height. Notice the height of its rebound. Now, drop the ball from the top floor on the ground and again notice the height of rebound of the ball.
You will observe that the ball will be rebound to a greater height when dropped on the ground than when it is dropped on the top floor. This is because the energy of the ball hitting the ground is greater than that hitting the floor. From where does the ball get a large amount of energy in the second case?
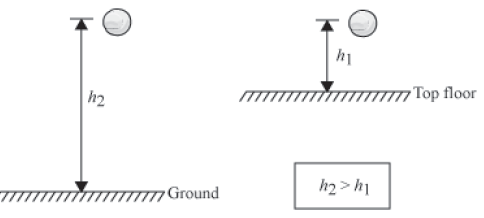
We know the fact that an object located at a height with respect to a certain reference level is said to possess energy called gravitational potential energy. This energy depends on this reference level (sometimes also referred as ground level or zero level). When a ball is taken to the top floor from the ground floor, it acquires some gravitational potential energy.
When this ball was dropped from a height h1 on the top floor, the zero level is the top floor itself. When the ball was dropped from a height h2 on the ground, the zero level is the ground. Since the distance covered by the ball was greater in the second case, i.e. h2 > h1, it rebounded to a greater height from the ground than that from the top floor.
Hence, we conclude from the above discussion that potential energy stored in a body is directly proportional to its height with respect to zero level.
Chemical Energy
Do you know how energy is stored in energy drinks or in a food item? The energy is stored in these items in the form of chemical energy. This kind of energy is stored as a bonding between the molecules. When we eat or drink, the food items undergo chemical changes. As result of this, the chemical bonding in the food items breaks and energy gets released. Not only food, all the fire items such as oil, kerosene, coal, wood, gunpowder have chemical energy stored in them.
Light Energy
You must have noticed that a material becomes hot when placed under the sun for a long time. If you place a paper under bright sunlight and hold a magnifying glass over it for a long time, then you will see that the paper starts burning. Why does all this happen? What kind of energy is responsible for this? The answer is light energy. Many
chemical reactions such as photosynthesis require light energy to start. Light energy also causes a reaction in the chemicals coated on a photographic film.
Heat Energy
Have you ever wondered about the process of cooking food? The food is cooked from
the heat produced by burning of fuel. This energy is known as heat energy. The sun is a perfect source of heat energy.
The amount of heat produced or released is measured in the unit “Calorie”.
Nuclear Energy
In order to understand nuclear energy, we should first understand nuclear fission reaction.
How is electricity produced in nuclear power plants?
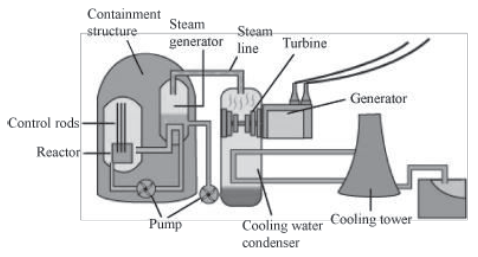
Nuclear power plants consist of nuclear reactors. These reactors use uranium rods as fuel and hen heat is generated by
the process of nuclear fission.
Neutrons smash into the nucleus of the uranium atoms, which roughly split into half and release energy in the form of heat.
Carbon dioxide gas is pumped through the reactor to take the heat away. The hot gas then heats water to form steam. This steam drives the turbines of generators to produce electricity.
Electrical Energy
You must have seen that electric fan stops rotating as the power goes off. This is because a fan uses electric energy for its rotation. As the electric power goes off, the energy supply to the fan stops and the fan stops rotating. Therefore, electric energy is another form of energy. In fact, in modern civilization, it is the most widely used form of energy. Everything from a small electric bulb to a heavy machine in a factory requires electric energy. Electricity can be used for producing light, heat, sound, and even chemical energy.
Magnetic Energy
Bring a magnet near an iron nail. What do you notice? The iron nail gets attracted towards the magnet and starts moving. You already know that movement means kinetic energy. But from where does the kinetic energy come to the nail?
The attraction of the magnet causes the movement of the nail. Therefore, the magnet must possess some kind of energy that does the work on the nail. This energy is called magnetic energy. Magnetic energy is broadly used in industries where heavy metal pieces are shifted from one place to another. In Japan, magnetic energy is used even for running high-speed trains.
Sound Energy
Have you ever noticed that when you play music at a very high volume, the glass pane of the windows or the showcase in your room starts vibrating? Why does this happen? This happens because of the high-volume sound. We call it sound energy. The interesting fact about sound energy is that it is produced because of vibration and causes vibration. When sound energy enters our ear and strikes the eardrum, it starts vibrating and thus, we can hear.
Principle of Conservation of Energy
What causes a ball dropped from a height to move? When an arrow is released from a bow, what causes the arrow to acquire kinetic energy?
Since a ball at a height and an arrow in the stretched string of a bow possess potential energy by virtue of their position and configuration respectively, they both acquire kinetic energy. However, does it mean that potential energy stored inside the ball or arrow is converted into kinetic energy?
We observe a number of examples in nature in which a form of energy is converted into another form. For example, the chemical energy of food we eat gets converted into muscular energy that can be used to do work such as cycling, walking, lifting a load, etc.
During cycling, the muscular energy of the cyclist is converted into the kinetic energy of the bicycle that moves him forward. One thing to be noted here is that the total energy of the system (cyclist + bicycle) remains unchanged i.e., muscular energy + kinetic energy remain unchanged during cycling.
Know this: There is an energy loss in the machines when they are running for a long time due to the friction between wheel and axle. This loss of energy or friction between wheel and axle can be reduced by using some lubricating substances like grease. Therefore to minimize the energy loss we should lubricate machines in regular interval of time.
Conservation of energy
“Energy cannot be created or destroyed. It can only be transformed from one form to another”. In other words, the total amount of energy in a system always remains constant.
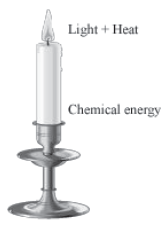
For example, in a burning candle, chemical energy stored in the wax is transformed into light and heat energy.
The total energy, before and after burning the candle, remains constant.
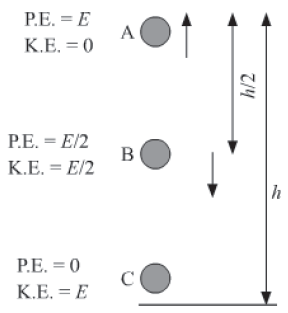
Total mechanical energy of a freely falling body always remains conserved provided friction due to air is neglected.
A body of mass m is falling freely under the action of gravity from the height h above the ground. At point A, the body posses maximum potential energy, say E. As this body falls down, its potential energy changes into the kinetic energy such that at point B, half of the potential energy changes to kinetic energy and at point C the total potential energy of the body changes to kinetic energy. Thus, at point C, the body posses only kinetic energy which will be equal to E. Hence the mechanical energy of the freely falling body remained conserved.

ICSE Class 10 Work Energy and Power Notes are one of the best materials that students can get, as it will help them to concentrate better and reduce the level of stress that students face during the furious year.
Notes are essential for conceptual understanding and scoring good marks, and for Revision, Revision Notes are always considered as the best when your exams are coming. We give ICSE Class 10 Work Energy and Power Notes in a straightforward, free downloadable PDF design for the students to figure out a better understanding of the topics.






