Students should refer to Sound ICSE Class 10 Physics notes provided below designed based on the latest syllabus and examination pattern issued by ICSE. These revision notes are really useful and will help you to learn all the important and difficult topics. These notes will also be very useful if you use them to revise just before your Physics Exams. Refer to more ICSE Class 10 Physics Notes for better preparation.
ICSE Class 10 Physics Sound Revision Notes
Students can refer to the quick revision notes prepared for Chapter Sound in Class 10 ICSE. These notes will be really helpful for the students giving the Physics exam in ICSE Class 10. Our teachers have prepared these concept notes based on the latest ICSE syllabus and ICSE books issued for the current academic year. Please refer to Chapter wise notes for ICSE Class 10 Physics provided on our website.
Sound ICSE Class 10 Physics
Waves – Transverse and Longitudinal
Waves
Continuous disturbance that transfers energy without any net displacement of the medium particles
Types of Wave
• Mechanical wave
• Requires a material medium for propagation
• Examples − sound waves, water waves, etc.
• Electromagnetic wave
• Does not require any material medium
• Examples − light wave, X-rays, etc.
• Matter wave
• Associated with electrons, protons, neutrons, atoms
Types of Mechanical Wave
• Transverse wave
• Medium particles oscillate perpendicular to the direction of propagation of wave.

• Transverse waves are transmitted through solids and not through liquids and gases as the latter does not possess any internal transverse restoring force (shear strength).
• Longitudinal waves
• Medium particles oscillate along the direction of propagation of wave.

• Longitudinal waves can propagate through solids, liquids, and gases.
Reflection of Sound
When you sing in the bathroom or shout in an open field, your sound gets reflected off various obstacles. This reflection of sound results in echo and reverberation. There is an old wives’ tale that a duck’s quack has no echo. The tale would be true if the duck quacks in your living room. However, in suitable conditions, a duck’s quack will surely echo.
When sound falls on a hard surface (solid or liquid), it bounces and changes its direction—just like light or a rubber ball. This bouncing back of sound on striking a surface is called reflection of sound.
Hard surfaces such as a metal box and concrete wall are good reflectors of sound waves. Soft surfaces such as a cushion are bad reflectors of sound because they absorb sound.
Laws of reflection of sound:
(i)The incident sound wave, the reflected sound wave and the normal to the surface at the point of incidence, all lie in the same plane, i.e., reflection is a two-dimensional phenomenon.
(ii)The angle of reflection of sound is always equal to the angle of incidence.
Quick Questions
Question 1: Is the law of reflection of sound similar to the law of reflection of light?
Solution: Yes, the two laws are similar.
Question 2: Does the frequency of sound change after reflecting off a surface?
Solution: No, it does not. The frequency of sound depends only on the source of sound.
Echo
The repetition of sound caused by its reflection off a hard surface is known as echo. If you shout once in an auditorium, then you will hear the original sound at first and then the reflected sound. This reflected sound is the echo of the original sound.
Echo
The sensation of a sound exists in the human brain for about 0.1 s. This means that if two sounds reach our ears within one-tenth of a second, then we will not hear them as separate sounds. So, if a reflected sound is to be heard separately from the original sound, there needs to be a time interval of at least one-tenth of a second (i.e., 0.1 s) between them
Now, we know that:
The speed of sound in air at 20°C is about 344 m/s.
The minimum time difference needed between a sound and its reflection for the echo to be heard is 0.1 s.
Therefore, the total distance travelled by the sound and its reflection to produce the echo is given as:
Total distance = Speed × Time
= 344 × 0.1 = 34.4 m
So, the sound travels 34.4 m during the time between which it is transmitted and the echo is heard. This distance is twice the actual distance between the source of the sound and the reflector of the sound. Therefore, the actual distance between the source of the sound and the reflector of the sound is 17.2 m.
Project Ideas
Visit your school auditorium with a friend. One of you should stand at a corner and the other should stand at the adjacent corner that is farther from it. One of you should clap. The other should measure the time interval between the clap and its echo using a stopwatch. Then, taking the speed of sound to be 330 m/s, calculate the distance between the two of you. Find out the actual length of the auditorium and compare it with the distance calculated.
Solved Examples
Medium
Example 1:
A person is standing between two vertical cliffs. He is 540 m away from the nearest cliff. He shouts and hears the first echo after 3 s. Calculate the speed of sound in air.
Solution:
Total distance covered by the sound and its reflection = 2 × 540 m
Time taken for the echo to be heard = 3 s
Let the speed of sound in air be v.

Example 2:
Rajeev claps his hands near a mountain and hears the echo of the sound after 6 s. If the speed of sound in air is 346 m/s, then calculate the distance between Rajeev and the mountain.
Solution:
Time taken for the echo to be heard = 6 s
The time taken by the sound to reach the mountain is half of the time taken for the echo to be heard, i.e., 3 s.
Speed of sound in air = 346 m/s
Let the distance between Rajeev and the mountain be s.
We know that:
Distance = Speed × Time
⇒ s = 346 × 3
∴ s = 1038 m
Reverberation
A sound produced in an auditorium exists for some time because it undergoes multiple reflections off the walls, ceiling and floor. This is called reverberation. The duration of an echo in this case is so short that several echoes overlap with the original sound. If the reverberation is too long, then the sound becomes distorted, noisy and confusing.
Solved Examples
Easy
Example 1:
A fishing boat using sonar detects a school of fish 150 m below it by transmitting an ultrasound signal. How much time elapses between the transmission of the signal and its return to the boat? (Speed of sound in sea water = 1500 m/s)
Solution:
It is given that:
Speed of sound in sea water = 1500 m/s
Distance between the boat and the fish = 150 m
Distance covered by the ultrasound signal = (2 × 150) m = 300 m
Let the time taken by the signal to return to the boat be t.

Medium
Example 2:
A man standing at a point between two parallel walls fires a pistol. He hears the first echo after 0.5 s and the second one after 0.7 s. Find the distance between the walls. (Speed of sound in air = 340 m/s)
Solution:
It is given that:
Speed of sound in air = 340 m/s
Time taken for the first echo to be heard = 0.5 s
Let the distance between the man and one of the walls be x. The sound and its echo travel double this distance.
We know that:

Now,
Time taken for the second echo to be heard = 0.7 s
Let the distance between the man and the other wall be y. The sound and its echo travel double this distance.
So,

Thus, distance between the two walls = x + y = 85 m + 119 m = 204 m
Hard
Example 3:
A woman, standing at a distance from a hill, fires a gun. She hears its echo after 3 s. Then, moving 350 m away from the hill, she fires again. This time she hears the echo after 5 s. Calculate the speed of sound in air.
Solution:
It is given that the first echo is heard after 3 s.
Let the distance between the woman and the hill be x. The sound and its echo travel double this distance.
Let the speed of sound in air be v.
We know that:

The woman then moves 350 m away and fires again. The time taken for the this echo to be heard is 5 s.
Let the new distance between the woman and the hill be x + 350. The sound and its echo travel double this distance.
So,

Uses of Echo
• For determination of speed of sound:

• Bats and dolphins use echo to detect obstacle or enemy in their path Also, they use it to hunt their prey.
• Bats and dolphins can produce and hear ultrasonic sound i.e sound of very high frequency of about 100 KHz. Thus, they have very high audible limit. Bats and dolphins produce high frequency sound waves which on striking any obstacle or prey on their path get reflected and start travelling towards them. On hearing these reflected sound
waves (the echoes of the waves produced by them), they detect the obstacles or the preys in their path. In this way, they protect them from colliding with the obstacles or hunt their preys. This process of detecting obstacles is known as sound ranging.
• Sonar is the acronym for Sound Navigation and Ranging. It is an acoustic instrument installed in ships to measure depth, direction and speed of underwater objects such as icebergs, sea rocks, shipwrecks and spy submarines. It uses high-frequency ultrasound for this purpose and works on the principle of echo.
Sonar consists of two main parts—the transducer and the detector. The former produces and transmits ultrasonic sound, while the latter receives the ultrasound reflected from the bottom of the sea or an underwater object. Sonar measures the echo of the ultrasound and calculates the depth or distance of underwater objects using the relation:
2d = v × t
Where, d = Distance between the ship and the underwater object
v = Speed of ultrasound in water
t = Time taken by the echo to return from the object
This method of measuring distance is known as echo ranging.
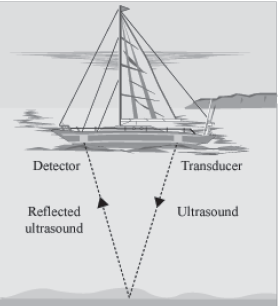
• In medical field: Here, echo method of ultrasonic waves is used to view human organs and any foreign body inside it.
Natural, Damped and Forced Vibration; Resonance
Natural vibrations
The periodic vibrations of a body in the absence of any external force on the body are known as natural or free vibrations. The frequency of the body in natural vibrations is called its natural frequency.
Few examples of natural or free vibrations:
• Simple pendulum: It starts vibrating with its natural frequency when its bob is displaced from its mean position. Its frequency depends upon length l of the pendulum and acceleration due to gravity g and is given by

• A load and spring system: Its frequency is given by

where K is force constant and m is the mass of the spring.
• Tuning fork when struck hard on a rubber pad starts vibrating with natural frequency.
• On plucking the strings of instruments like sitar, guitar, violin, etc, vibrations of a definite natural frequency are produced. This natural frequency is given as

where d is the density of the material and πr2d is the mass of the unit length of the string. The frequency f of vibrations in a stretched string is
• inversely proportional to length and radius of the string
• directly proportional to the square root of the tension (T) in the string
• A string of a given length stretched between its ends under a given tension can be made to vibrate in different modes by plucking the string at different points.

In figure (a), the string of length l is stretched in the middle because of which it vibrates in one loop. This vibration is known as principle note of frequency f. When the same string is plucked at its 1/4 length from one end, it vibrates in two loops (figure (b)).
Similarly, when it is plucked at its 1/6 length from one end, it vibrates in three loops (figure (c)).The wavelength of different modes in figure (a), (b) and (c) is 2l, 2l/2 and 2l/3, respectively.
Nature of natural vibrations
The natural vibrations are the simple harmonic vibrations under the influence of restoring force for which the amplitude and frequency continue to remain constant. These natural vibrations are possible only in vacuum.
In actual practice, it is impossible to achieve natural vibrations as the surrounding always has some form of medium which offers resistance to the motion or vibrations of a body because of which the amplitude of vibrations goes on decreasing. The frequency of natural vibration depends on the shape and size of the vibrating body.

Damped vibrations
The periodic vibrations of a body of decreasing amplitude in the presence of any resistive force are called damped vibrations. Two forces which take part in damped vibrations are:
• the restoring force
• the frictional or resistive force
The reason for damped vibrations is the frictional or resistive force due to the surrounding medium. This resistive force has the tendency to oppose the motion of a body and, at any instant, is proportional to the velocity of the body (=mv/t). Thus, the energy of vibrating body continuously gets dissipated for overcoming this resistive force due to which the amplitude of its vibrations goes on decreasing. Ultimately, the body stops vibrating when it loses all its energy. The rate of decrease of amplitude of vibrations depends on
• nature of the medium
• shape and size of the body in vibrations

Few examples of damped vibrations:
• Thin branch of a tree when pulled and released produces damped vibrations.
• Tuning fork when struck on a rubber pad in the presence of air produces damped vibrations.
• Simple pendulum oscillating in air produces damped vibrations.
• Vibrations of a loaded spring in air are damped vibrations.
Forced vibrations
The vibrations of a body which take place under the influence of an external periodic force acting on it, are called the forced vibrations. The forces which take part in forced vibrations are:
• the restoring force
• the frictional or resistive force
• the external periodic force or driving force
In forced vibration, the body vibrates with the frequency of the applied force and not with its natural frequency. The amplitude of forced vibrations depends on the frequency of the driving force. The amplitude of forced vibrations will be very large if the frequency of driving force is exactly equal to the natural frequency of the body and if these two
frequencies are different, then the amplitude of forced vibration will be small.
Few examples of forced vibrations:
• Vibrations produced in the table top when a vibrating tuning fork is pressed against it are forced vibrations.
• Vibrations produced in the microphone’s diaphragm with the frequencies corresponding to the speech of the speaker is an example of forced vibrations.
• In string instruments like guitar, an artist applies the periodic force on the strings to produce forced vibration in them.
Resonance
It is a special case of forced vibration in which the frequency of the externally applied periodic force on an object is equal to its natural frequency. In this case, the body begins to vibrate with an increased amplitude. This phenomenon is known as resonance.
Demonstration of resonance
(1) Resonance achieved using tuning forks and sound boxes

In the above set up, two tuning forks A and B of same frequency are mounted on two separate sound boxes with their open ends facing each other. Now, when the prong of one of the forks say, A strikes on a rubber pad, then it starts vibrating. Then it passes its forced vibration to the air column of the sound box placed below it.
These vibrations are of large amplitude because of large surface area in the sound box. Gradually vibrations produced by the sound box of fork A get communicated to the sound box of fork B. Now, the sound box of fork of B starts vibrating with the frequency
of fork A. Since, the frequency of these vibrations is same as the natural frequency of the fork B.
The fork B picks up these vibrations and starts vibrating under resonance. Hence, the two sound boxes help in communicating the vibrations and in increasing the amplitude of vibrations.
(2) Forced and resonant vibrations of pendulums

We have a set up in which four pendulums are suspended from a rubber string of length PQ. Pendulum A and B are of the same length so that their natural frequency of vibration is same. The pendulum C is shorter than A and B and pendulum D is longer than A and B. Hence, the natural frequency of C is higher than that of A and B and natural frequency of D is lower than that of A and B.
Initially, the pendulum A is set into vibration by displacing its bob to one of its side. We will observe that pendulum B which is of the same length as of pendulum A also starts vibrating with some small amplitude initially and then gradually acquires the same amplitude as of pendulum A.
The vibrations produced in pendulum A are communicated as forced vibration to the other pendulums through the rubber string PQ. But the pendulum C and D remain in the state forced vibrations while pendulum B comes in the state of resonance.
This happens because the length of pendulum A and B are same which results in the same natural frequency of both the pendulums. And therefore there is an exchange of energy only between A and B and thus the resonance takes place between them. Few examples where resonance can be seen:
• in machine parts
• in a bridge
• in radio and TV receivers
Characteristics of Sound Waves
Characteristics of Sound: An Overview
We can distinguish the sounds made by two men, two women, two musical instruments, two animals, etc. This is because sound waves differ in their quality or timbre. Quality is a characteristic of sound that enables us to distinguish between sounds with the same loudness and pitch. The following figures show the sound waves produced by a violin
and a flute.

A pleasant sound has a rich quality. The sound of a violin is more pleasant than that of a flute. This is evident from their respective sound waves.
These sound waves depict the voices of a boy and girl. Can you identify the girl’s sound wave?

Did You Know?
Two sounds with the same loudness, pitch and speed can be distinguished by their quality or timbre. If a sound is pleasant to hear, then it is said to have a rich timbre. An unpleasant sound has a poor timbre.
Characteristics of Sound
Sound is a longitudinal wave. A longitudinal wave manifests alternate regions of compressions and rarefactions while travelling through a medium. A longitudinal wave can be described by the five characteristics listed below.
• Amplitude
• Wavelength
• Frequency
• Time period
• Speed
These five characteristics are demonstrated in the following figure with the help of a transverse wave. Note that the crests and troughs in a transverse wave are equivalent to the compressions and rarefactions in a longitudinal wave, respectively.

Amplitude (A)
The amplitude (A) of a wave is the maximum displacement of the medium particles on either side of their original, undisturbed position. In the following figure, the transverse equivalent of a longitudinal sound wave is shown.

The maximum displacement of the medium particles is represented by the maximum
heights MP, ER and IT, and the maximum depths QC and SG. This maximum
displacement is the amplitude of the wave, i.e. MP = ER = IT = QC = SG = Amplitude of
the wave.
•The SI unit of amplitude is metre (m).
•The loudness of a sound is directly related to its amplitude. The amplitude of a loud sound is larger than that of a soft sound.
•The amplitude of a sound wave determines the amount of energy it carries.
Did You Know?
The loudness of a sound is directly related to the amplitude of the wave. It is the measure of our ears’ response to a sound. Our ears detect louder sounds better than softer ones. A loud sound has greater amplitude than a soft sound.
Whiz Kid
Loudness and Intensity
It is quite common to use the terms ‘loudness’ and ‘intensity’ interchangeably. However, the two are not the same.
Loudness is the measure of the human ear’s response to a sound. In contrast, intensity is the amount of energy passing per unit area per unit time.
•A sound may be louder than another owing to a difference in their intensities.
Can you say which sound wave corresponds to the louder sound?

Wavelength (λ)

The distance between two consecutive compressions or rarefactions of a sound wave is its wavelength (λ). In case of a transverse wave, wavelength is the distance between two consecutive crests or troughs.
In the figure, the distances BF and DH represent the wavelength of the wave.
The SI unit of wavelength is metre (m).
Can you say which of these two waves has the longer wavelength ?
Frequency (f)
The frequency (f) of a source of sound is the number of cycles or vibrations produced by it per second. It is the rate at which sound wave is produced by the source.
If five crests of a wave pass through a fixed point in one second, then the frequency of the wave is five cycles per second.
The SI unit of frequency is hertz (Hz).
One hertz is equal to one vibration per second. Sometimes a bigger unit of frequency— called kilohertz (kHz)—is used.
1 kHz = 1000 Hz
The frequency (f) of a wave is the reciprocal of its time period T, i.e.
f = 1/T
Note that the frequency of a wave is the same as the frequency of the vibrating body that produces the wave. For example, the frequency of a tuning fork is marked as 256 Hz. This means that it can produce a sound wave of frequency 256 Hz.
The frequency of a wave remains constant in any medium, but its speed and wavelength depend upon the nature of the medium.
Did You Know?
Pitch, Tone and Note
Pitch is defined as the shrillness of a sound. This highness or lowness of a sound is proportional to the frequency of the sound.
The sound produced by a flute is of a higher pitch compared to the sound produced by a drum. This is because the frequency of the former is higher than that of the latter.
Similarly, women produce higher-pitched sounds than men.
Tone is defined as a sound that has a single frequency.
Note is defined as a sound that has a mix of different frequencies.
Suppose two sounds, produced from two different sources, have the same amplitude and speed. In this case, one sound can be distinguished from the other by its pitch, which is directly related to its frequency. The female voice is high-pitched while the male voice is low-pitched.

Quality or Timbre is that characteristic of a sound that helps in distinguishing various types of sounds having same amplitude and frequency, but emitted from different sources. Quality of sound depends on its waveform.
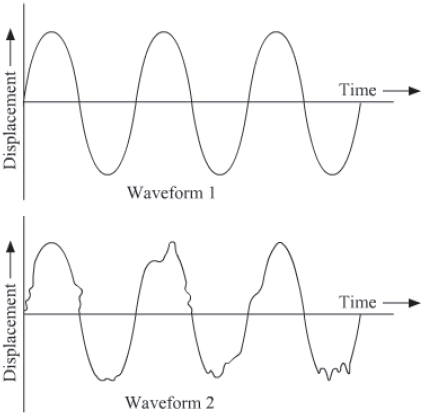
Both the sounds shown above have different quality as their waveforms are different.
Whiz Kid

Take a wide tub filled with water. Drop a pebble at the centre of the tub from a height. You will observe ripples moving outwards in a transverse-wave-like motion. Count the number of crests that hit a particular side of the tub. Note the time using a stopwatch. Then, calculate the frequency of this wave. Share your result with friends.
Know Your Scientist

Heinrich Rudolph Hertz (1857-1894) was a German scientist. He was educated at the University of Berlin. He confirmed James Clark Maxwell’s electromagnetic theory through his experiments. He laid the foundation for the future development of the radio, telephone, telegraph and television. He died quite young, less than a month before his
thirty-seventh birthday. The SI unit of frequency is named in his honour.
Sonic Boom
Sonic boom occurs when an aircraft breaks the sound barrier. An aircraft travelling with a supersonic speed will produce a pressure wave of sound in the shape of a cone whose vertex will be formed at nose of the aircraft and its base will be behind the aircraft. So, when the edge of the cone intersects with our ears, we hear a loud sound
known as sonic boom.
Time Period (T)
The time required to complete one complete oscillation or cycle is called the time period (T). It is also defined as the time interval between two consecutive crests or troughs of a wave.
• The SI unit of time period is second (s).
• It is the inverse of the frequency of a wave, i.e. T = 1/f.

A flat sound is a low-pitched sound.
This is a periodic wave. Its time period is represented by length on the time axis,
e.g. ab, cd and ef.
Solved Examples
Easy
Example 1:
The frequency of a source of sound is 400 Hz. Calculate the number of times the source vibrates in one minute. Also calculate the time period.
Solution:
Frequency of the source of sound = 400 Hz
Number of vibrations of the source per second = 400
Number of vibrations of the source per minute = 400 × 60 = 24000
We know that time period (T) is the inverse of frequency (f). So,

Speed
The distance travelled by a wave in a given interval of time is called its speed (v). Its SI unit is metre per second (m/s). Hence, we can write:

Suppose a wave can travel a distance λ in T seconds with a speed v. Then, these terms are related as follows:

We know that
f = 1/T
So,
v = f × λ
Therefore, speed is the product of frequency and wavelength.
Now, the sound travels with much greater speed in solids than in liquids and than in gases.

Did You Know?
According to Albert Einstein’s special theory of relativity, nothing can travel faster than the speed of light. The speed of light in air (3 × 108 m/s) is about 10,00,000 times greater than the speed of sound in air (344 m/s).
Solved Examples
Easy
Example 1:
What is the speed of sound with frequency 20 Hz and wavelength 0.2 m?
Solution:
Speed (v) = Frequency (f) × Wavelength (λ)
= 20 × 0.2 = 4 m/s
Example 2:
f twenty pulses are produced per second, then what is the frequency of the wave in hertz?
Solution:
The frequency of a wave in hertz is equal to the number of pulses produced per second.
Number of pulses produced by the wave per second = 20
Frequency of the wave = 20 Hz
Medium
Example 3:
A sound wave travelling at a speed of 330 ms-1 has a wavelength of 2 cm.
Calculate the frequency of the wave. Will it be audible to humans?
Solution:
Speed of the sound wave = 330 m/s
Wavelength = 2 cm = 0.02 m
We know that

Hence, the frequency of the sound wave is 16.5 kHz.
ow, we know that human hearing ranges from 20 Hz to 20 kHz. Since the frequency of the given sound wave is 16.5 kHz, it will be audible to humans.
Example 4:
Sound waves travel at a speed of 330 m/s. Calculate the frequency of a sound wave whose wavelength is 0.75 m.
Solution:
• Distance from the source
Given:
Speed (v) of the wave= 330 m/s
Wavelength λ = 0.75 m
We have to find the frequency (f) of the wave.
We know that

Hence, the frequency of the sound wave is 440 Hz.
Hard
Example 5:
A wave pulse on a string moves a distance of 10 m in 0.05 s. Find the velocity of the pulse and the wavelength of the wave if its frequency is 300 Hz.
Solution:
We know that

Therefore, the speed or velocity of the pulse is 200 m/s.
We also know that
Speed = frequency × wavelength
In the given case:
Frequency = 300 Hz

Therefore, the wavelength of the wave is 0.67 m.
Whiz Kid
Attach one end of a coiled spring to a wall. Compress the spring and then release it. You will observe a longitudinal wave produced in the spring, with alternating compressions and rarefactions. Count the number of compressions or rarefactions passing from the fixed point. Note the time using a stopwatch. Then, calculate the frequency of this wave.

Factors Affecting the Speed of Sound
We know that sound waves require a medium to travel. The temperature, humidity and nature of a medium affect the speed of sound travelling through it. Let us see how.
Temperature
The temperature of a medium is directly related to the speed of sound travelling through it. The speed of sound increases with an increase in the temperature and decreases with a decrease in the temperature. For example, the speed of sound in air at 0°C is about 332 m/s whereas its speed in air at 25°C is about 346 m/s.
Humidity
Like temperature, humidity is directly related to the speed of sound. For example, the speed of sound in dry air is 334 m/s; in moist air, it is 338 m/s.
Nature
The speed of sound varies according to the nature of the medium it travels through. The speed of sound in a gaseous medium is less than that in a liquid medium. Also, the speed of sound in a liquid medium is less than that in a solid medium.
For example, at 25°C, the speeds of sound in hydrogen, water and iron are about 1284 m/s, 1500 m/s and 5130 m/s respectively. Hence, we can conclude that
vg < vl < vs
Here, vg = Speed of sound in a gaseous medium; vl = Speed of sound in a liquid
medium; vs = Speed of sound in a solid medium
Whiz Kid
The given table lists the speeds of sound in various materials at different temperatures.
| Medium | Temperature (°C) | Speeds of sound (in m/ s) |
| dry air | 0 | 332 |
| dry air | 20 | 344 |
| dry air | 25 | 346 |
| Hydrogen | 0 | 1280 |
| Hydrogen | 25 | 1284 |
| Distilled water | 20 | 1498 |
| Sea water | 37 | 1531 |
| Blood | 20 | 1570 |
| copper | 20 | 3750 |
| Aluminium | 20 | 5100 |
| Aluminium | 25 | 6420 |
| iron | 20 | 5130 |
| glass | 20 | 5170 |
Did You Know?
Here is an interesting natural phenomenon related to the speed of sound. When lightning strikes, the flash is seen a few seconds before the sound is heard. Why does this happen?
This happens because the speed of sound in air (332 m/s) is much less than that of light (300000000 m/s). Hence, there is a difference between the time taken by the two to cover the same distance.
Here are two other phenomena indicating that light travels faster than sound.
1. When a cracker bursts, we first observe the light and then hear the sound.
2. When a gun is fired from a distance, we first notice the flash of the gun and then hear the gunshot.
Solved Examples
Easy
Example 1:
A person hears a thunder four seconds before the flash of lightning. What is the distance between the person and the point where lightning occurs in the sky?(Speed of sound in air = 330 m/s)
Solution:
We know that

In this case:
Speed = 330 m/s
Time = 4 s
Distance = Speed × Time
= 330 × 4 = 1320 m
Hence, the distance between the person and the point of lightning in the sky is 1320 m
or
1.32 km.
Hard
Example 2:
Ravinder throws a stone vertically upward with a velocity of 50 m/s. It hits a bell hanging at a height of 125 m. The bell rings as the stone hits it. How long after his throw will Ravinder hear the ring of the bell? (Take the speed of sound as 344 m/s and acceleration due to gravity as 10 m/s2.)
Solution:
Let us first calculate the time taken (t) by the stone to reach a height of 125 m.
We have the following motion relation:
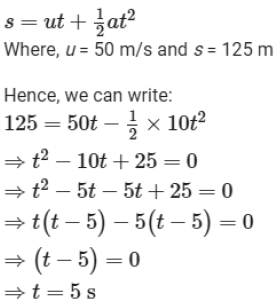
Now, let us calculate the time taken (t’) by the sound of the ring to reach the ground. We can do so by dividing the height of the bell by the speed of sound.

Hence, Ravinder will hear the sound of the ring 5.36 (5 + 0.36) seconds after his throw.
Musical Sound
Sound maybe of two types: noise and musical sound. Musical sounds are produced by musical instruments like flute, guitar, violin, etc. They produce a pleasant effect on the listener. On the other hand, noise is produced by a person’s shouts, thunderstorm etc. They produce an unpleasant effect on the listener.
Characteristics of musical sound:
(i) Loudness – This characteristic property of sound distinguishes two sounds of same frequency. It depends upon the intensity of vibration, which is proportional to the square of amplitude. So, larger the amplitude, louder is the sound. Loudness also depends on the following factors:
• Density of air
• Sensitivity of the ear
• Distance from the source
• Velocity and direction of wind
(ii) Pitch – Pitch is the characteristic of sound which differentiates the notes. Pitch of the sound depends on the frequency of the sound. A sound is said to have high pitch or is shrill if it is produced by a vibrating body of high frequency. If a body vibrates with low frequency, then it produces a flat sound. For example, a male voice is flat while a
female voice is shrill.
(iii) Quality – Quality is the characteristic of sound that differentiates two sounds of same pitch and loudness. The sound produced by the musical instruments are made up of waves of definite frequency but contain a series of tones of different frequencies.
They are called Overtones and the tone of smallest frequency is called the fundamental tone. Larger the number of overtones, higher is the quality of sound.((i
Musical scale:
When two notes are sounded simultaneously and produce a pleasant sensation in the ear, then it is a concord or a consonance.
If the notes produce an unpleasant sound in the ear, then it is a dischord or a dissonance.
Harmony – Harmony is the pleasant effect produced due to concord, when two or more notes are sounded together.
Melody – Melody is the pleasant effect produced by two or more notes, when they are sounded one after the another.
Musical intervals – Musical interval is the ratio of frequencies of two notes in the musical scale.
Musical scale – Musical scale is the series of notes separated by a fixed musical interval. Keynote is the starting note of a musical scale.
A diatonic scale contains a series of eight notes.
An octave is the interval between the keynote and the last tone.
Advantages of a diatonic scale
• This scale provides the same order and duration of chords and intervals, which succeed each other, that are required for a musical effect.
• This scale can produced a musical composition with the lower and higher multiples of frequencies of the notes.
Loudness and Intensity
Loudness of sound
Loudness is the characteristic of sound by virtue of which a loud sound can be distinguished from a feeble one, both having the same pitch and timbre. It depends upon the amplitude of the wave. The unit of loudness is phone and decibel (dB).

On comparing the waves of the above graphs, which are produced on striking a tuning fork with a rubber band first gently and then strongly, we observe two waves have same frequency (i.e. same pitch) and same waveform (i.e. same quality or timbre) , but they differ in amplitude. Evidently, the loud sound corresponds to the wave of the large
amplitude.
Loudness of sound
• is directly proportional to the square of amplitude
• inversely varies with the square of distance from the source
• is directly proportional to the surface area of vibrating body
• is directly proportional on the density of the medium
• increases with the presence of resonating bodies near the vibrating body
Intensity of sound
It is the amount of sound energy passing per second normally through the unit area around a point in a medium. Its unit is watt per meter2 .
The intensity of sound wave is proportional to
• square of the amplitude of vibration
• square of the frequency of vibration
• density of air
Subjective nature of loudness and objective nature of intensity
The loudness of a sound depends on (1) intensity and (2) sensitivity of the ears of the listener i.e. the sound of the same intensity may appear to be of different loudness to different persons.
Moreover, two sounds of the same intensity but of different frequencies may differ in loudness to the same listener because listeners’ ears are sensitive to different frequencies.
Thus, loudness is subjective in nature but intensity is objective in nature as it being a measurable quantity.
Relationship between loudness and Intensity
According to the Weber and Fechner, relationship between loudness and intensity is given as
L = K log10 I
Here, K is the constant of proportionality.
For an equally loud pure sound of frequency 1 kHz, the loudness of a sound in phon is the loudness in decibel.
Let I1 and I0 be the intensities of two sounds of loudness L1 and L0, respectively. Using the relation between loudness and intensity, we have
L1 = K log10 I1 and L0 = K log10 I0
If taking L as the difference of loudness of two sounds, then
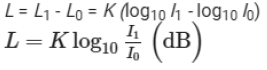
Noise pollution
Noise pollution is the disturbance produced by noise which has harmful impact on humans and animals. When sounds of level above 120 dB is produced from various sources such as loudspeakers, moving vehicles etc., then such sounds are reffered as noise. Now, when these sounds of level above 120 dB are constantly heard, then these can cause severe headache or permanent damage to the ears of listeners. Sounds with such level also have adverse effects on various birds and animals.







