Question 1. Calculate the co-ordinates of the point P which divides the line segment joining:
(i) A (1, 3) and B (5, 9) in the ratio 1: 2.
(ii) A (-4, 6) and B (3, -5) in the ratio 3: 2.
Solution:
(i) Let us assumed that, co-ordinates of the point P be (x, y)
We know that
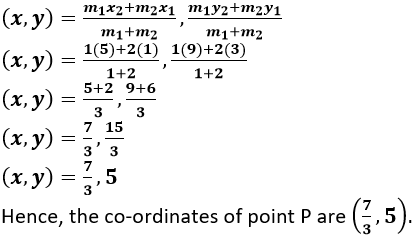
Question 2. In what ratio is the line joining (2, -3) and (5, 6) divided by the x-axis.
Solution:
It is given that, the joining points A (2,-3) and B (5,6) divided by the x-axis by the point P(x,0).
Let the ratio is k:1.
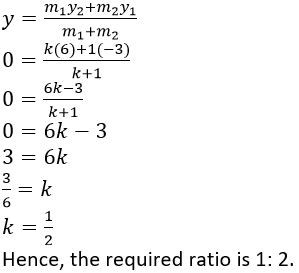
Question 3. In what ratio is the line joining (2, -4) and (-3, 6) divided by the y-axis.
Solution:
It is given that, the joining points A (2,-4) and B (-3, 6) divided by the x-axis by the point P(0, x).
Let the ratio is k:1.
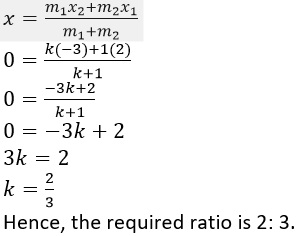
Question 4. In what ratio does the point (1, a) divided the join of (-1, 4) and (4, -1)? Also, find the value of a.
Solution:
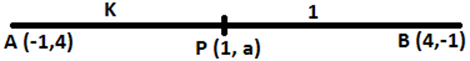
It is given that, the joining points A (-1, 4) and B (4, -1) divided by the x-axis by the point P (1, a). Let the ratio is k: 1

Question 5. In what ratio does the point (a, 6) divide the join of (-4, 3) and (2, 8)? Also, find the value of a.
Solution:
It is given that, the joining points A (-4, 3) and B (2, 8) divided by the x-axis by the point P (a, 6).
Let the ratio is k: 1.

Question 6. In what ratio is the join of (4, 3) and (2, -6) divided by the x-axis. Also, find the co- ordinates of the point of intersection.
Solution:
It is given that, the joining points A (4, 3) and B (2, -6) divided by the x-axis by the point P (x, 0).
Let the ratio is k: 1.
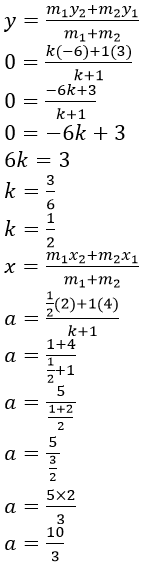
Hence, the required ratio is 1: 2 and the value of a is 10/3.
Question 7. Find the ratio in which the join of (-4, 7) and (3, 0) is divided by the y-axis. Also, find the coordinates of the point of intersection.
Solution:
It is given that, the joining points A (-4, 7) and B (3, 0) divided by the x-axis by the point P (0, y).
Let the ratio is k: 1
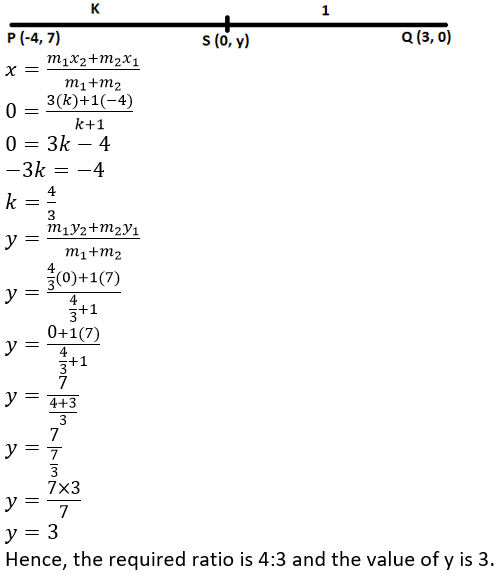
Question 8. Points A, B, C and D divide the line segment joining the point (5, -10) and the origin in five equal parts. Find the co-ordinates of A, B, C and D.
Solution:

The coordinates of point A is (3,-6).
Point C divides the line PO in the ratio 3:2.

Question 9. The line joining the points A (-3, -10) and B (-2, 6) is divided by the point P such that

Solution:
Let us assumed that, the co-ordinates of Point P (x, y)
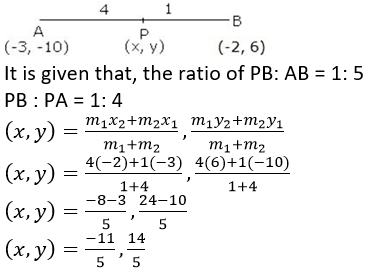
Question 10. P is a point on the line joining A (4, 3) and B (-2, 6) such that 5AP = 2BP. Find the co- ordinates of P.
Solution:
It is given that, 5AP = 2BP
AP/BP=2/5
Co-ordinates of the point P are
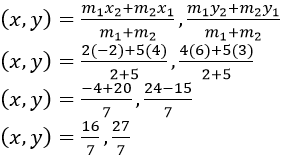
Question 11. Calculate the ratio in which the line joining the points (-3, -1) and (5, 7) is divided by the line x = 2. Also, find the co-ordinates of the point of intersection.
Solution:
It is given that, the points are (-3, -1) and (5, 7) is divided by the line x = 2, will be of the type (2, y).

Question 12. Calculate the ratio in which the line joining A (6, 5) and B (4, -3) is divided by the line y = 2.
Solution:
It is given that, the point A (6, 5) and (4, -3) is divided by the line y = 2, will be of the type (x, 2).
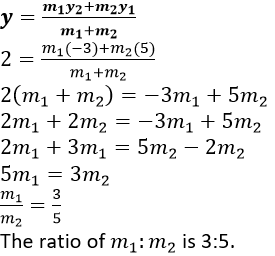
Question 13. The point P (5, -4) divides the line segment AB, as shown in the figure, in the ratio 2: 5. Find the co-ordinates of points A and B.
Solution:
It is given that, the point P (5, -4) divides the line segment AB, as shown in the figure, in the ratio 2: 5.
Here, Point A lies on x-axis, so the coordinates of A be (x, 0) and B lies on y-axis so, the coordinates of B be (0, y).
We know that, the section formula,
Question 14. Find the co-ordinates of the points of trisection of the line joining the points (-3, 0) and (6, 6).
Solution:
It is given that, the co-ordinates of the points of trisection of the line joining the points (-3, 0) and (6, 6). AP=PQ=QB
Here,
AP:PB =1:2
Coordinates of the points P,

Question 15. Show that the line segment joining the points (-5, 8) and (10, -4) is trisected by the co- ordinate axes.
Solution:
It is given that, the co-ordinates of the points of trisection of the line joining the points (-5, 8) and (10, -4). AP=PQ=QB
Here,
AP:PB =1:2
Coordinates of the points P,
Question 16. Show that A (3, -2) is a point of trisection of the line-segment joining the points (2, 1) and (5, -8). Also, find the co-ordinates of the other point of trisection.
Solution:
It is given that, the co-ordinates of the points of trisection of the line joining the points (2, 1) and (5, -8). PA=AB=BQ
Here,
PA:AQ=1:2
Coordinates of the point A.

Question 17. If A = (-4, 3) and B = (8, -6)
(i) Find the length of AB.
(ii) In what ratio is the line joining A and B, divided by the x-axis?
Solution:
(i) It is given that,
Points of A = (-4, 3) and B = (8, -6)

Question 18. The line segment joining the points M (5, 7) and N (-3, 2) is intersected by the y-axis at point L. Write down the abscissa of L. Hence, find the ratio in which L divides MN. Also, find the co-ordinates of L.
Solution:
It is given that L lines on y-axis coordinate on y axis are 0. Let P be the point on the x-axis that divides AB in the ratio k: 1

Question 19. A (2, 5), B (-1, 2) and C (5, 8) are the co-ordinates of the vertices of the triangle ABC. Points P and Q lie on AB and AC respectively, such that AP: PB = AQ: QC = 1: 2.
(i) Calculate the co-ordinates of P and Q.
(ii) Show that PQ = 1/3 BC.
Solution:
(i) It is given that, A (2, 5), B (-1, 2) and C (5, 8) are the co-ordinates of the vertices of the triangle ABC.
Coordinates of P are,


Question 20. A (-3, 4), B (3, -1) and C (-2, 4) are the vertices of a triangle ABC. Find the length of line segment AP, where point P lies inside BC, such that BP: PC = 2: 3.
Solution:
It is given that, the ratio of BP:PC is 2:3.
Here,
Coordinates of P are,

Question 21. The line segment joining A (2, 3) and B (6, -5) is intercepted by x-axis at the point K. Write down the ordinate of the point K. Hence, find the ratio in which K divides AB. Also, find the co-ordinates of the point K.
Solution:
It is given that, the line segment joining A (2, 3) and B (6, -5) is intercepted by x-axis at the point K, So, its ordinate is 0.
Let us assumed that, point k(x,0) divides AB in the ratio k:1
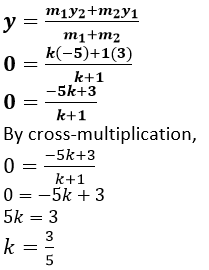

Question 22. The line segment joining A (4, 7) and B (-6, -2) is intercepted by the y-axis at the point K. Write down the abscissa of the point K. Hence, find the ratio in which K divides AB. Also, find the co-ordinates of the point K.
Solution:
It is given that, the line segment joining A (4, 7) and B (-6, -2) is intercepted by the y-axis at the point K.
Let us assumed that, point k(0,y) divides AB in the ratio k:1.
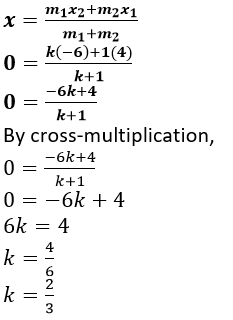

Question 23. The line joining P (-4, 5) and Q (3, 2) intersects the y-axis at point R. PM and QN are perpendiculars from P and Q on the x-axis. Find:
(i) the ratio PR: RQ.
(ii) the co-ordinates of R.
(iii) the area of the quadrilateral PMNQ.
Solution:
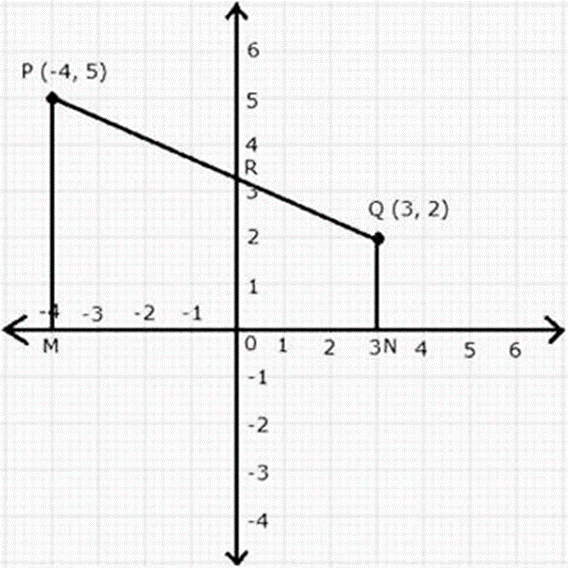
(i) It is given that, the line joining P (-4, 5) and Q (3, 2) intersects the y-axis at point R. Let us assumed that, point R (0,y) PQ in the ratio k:1.


Question 24. In the given figure, line APB meets the x-axis at point A and y-axis at point B. P is the point (-4, 2) and AP: PB = 1: 2. Find the co-ordinates of A and B.
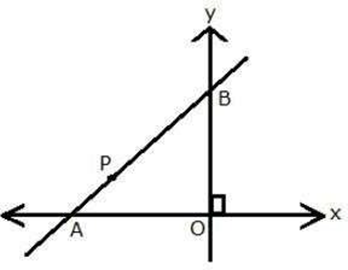
Solution:
It is given that, line APB meets the x-axis at point A and y-axis at point B. Let the co-ordinates of A and B be (x, 0) and (0, y) respectively. P is the point (-4, 2) and AP: PB = 1: 2.
By Section formula,
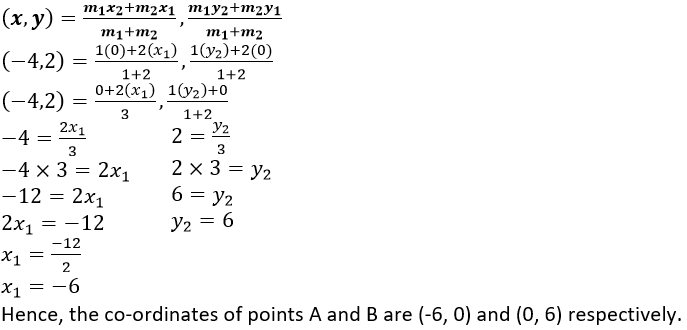
Question 25. If P(-b,9a–2) divides the line segment joining the points A(-3,3a+1) and B(5,8a) in the ratio 3: 1, find the values of a and b.
Solution:
It is given that, (x1, y1) = (-3, 3a+1); (x2, y2) = B (5, 8a) and (x, y) = (-b, 9a – 2)
m_1=3 and m_2=1
Coordinate of P(x, y)
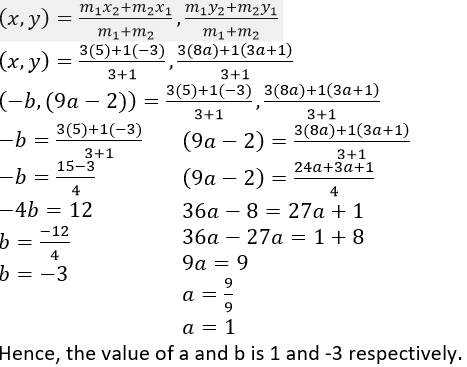
Exercise 13B
Question 1. Find the mid-point of the line segment joining the points:
(i) (-6, 7) and (3, 5)
(ii) (5, -3) and (-1, 7)
Solution:
(i) It is given that, A(-6, 7) and B(3, 5)

Question 2. Points A and B have co-ordinates (3, 5) and (x, y) respectively. The mid-point of AB is (2, 3). Find the values of x and y.
Solution:
It is given that, points A and B have co-ordinates (3, 5) and (x, y) and mid-point of AB is (2, 3).
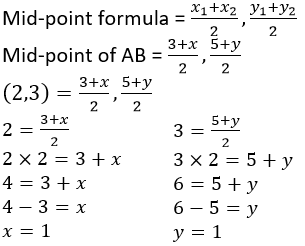
Question 3. A (5, 3), B (-1, 1) and C (7, -3) are the vertices of triangle ABC. If L is the mid-point of AB and M is the mid-point of AC, show that LM = 1/2 BC.
Solution:
It is given that, A (5, 3), B (-1, 1) and C (7, -3) are the vertices of triangle ABC. L is the mid-point of AB and M is the mid-point of AC.
Here,
Co-ordinates of L are,


Question 4. Given M is the mid-point of AB, find the co-ordinates of:
(i) A; if M = (1, 7) and B = (-5, 10)
(ii) B; if A = (3, -1) and M = (-1, 3).
Solution:
(i) It is given that, M is the mid-point of AB.
Let the co-ordinates of A be (x, y)
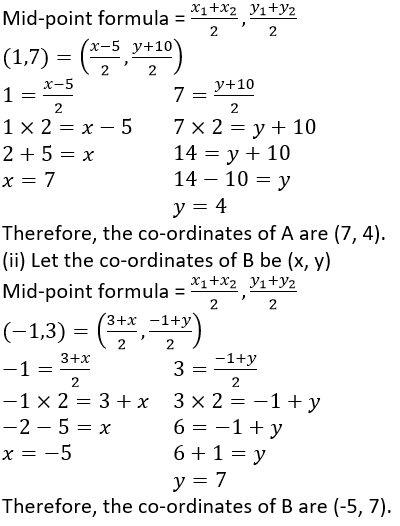
Question 5. P (-3, 2) is the mid-point of line segment AB as shown in the given figure. Find the co- ordinates of points A and B.
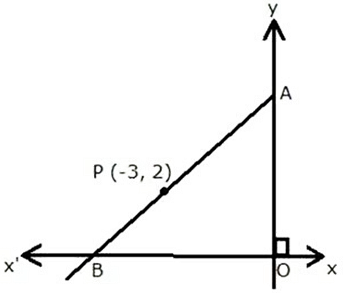
Solution:
It is given that, P (-3, 2) is the mid-point of line segment AB. Let us assumed that the co-ordinated of point A be (0,y) and B be (x,0).
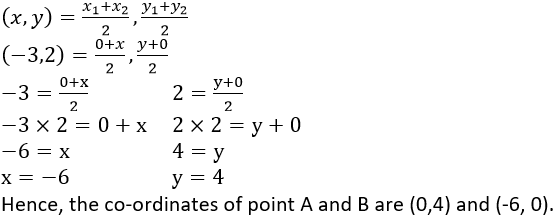
Question 6. In the given figure, P (4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
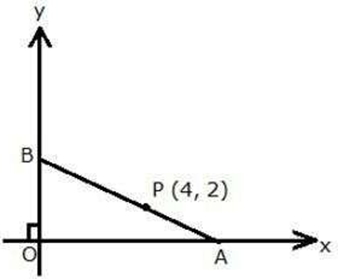
Solution:
It is given that, P (4, 2) is the mid-point of line segment AB. Let us assumed that the co-ordinated of point A be (x,0) and B be (0,y).
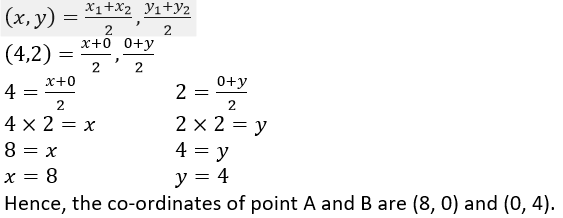
Question 7. (-5, 2), (3, -6) and (7, 4) are the vertices of a triangle. Find the lengths of its median through the vertex (3, -6).
Solution:
It is given that, A (-5, 2), B (3, -6) and C (7, 4) be the vertices of the given triangle.
Let us assumed that, D is the median of AB, E is the median of BC and F is the median of CA.
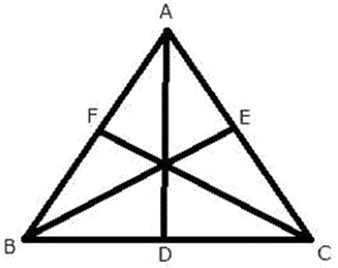
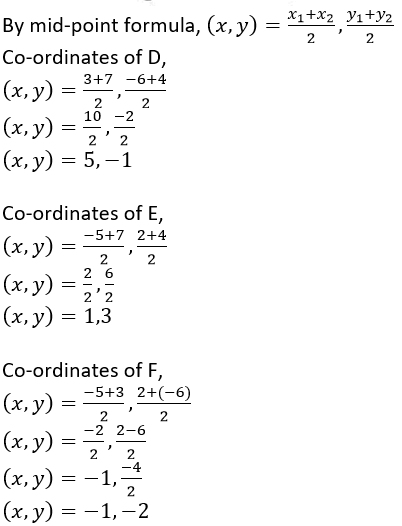
The median of the triangle through the vertex B (3,-6) is BE. Here, coordinates of B (3, -6) and coordinate of E (1,3) We know that the distance formula,
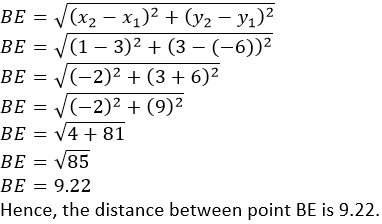
Question 8. Given a line ABCD in which AB = BC = CD, B = (0, 3) and C = (1, 8). Find the co-ordinates of A and D.
Solution:
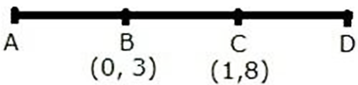

Question 9. One end of the diameter of a circle is (-2, 5). Find the co-ordinates of the other end of it, if the centre of the circle is (2, -1).
Solution:
It is given that, the coordinated of the diameter of a circle is (-2, 5) and the centre of the circle is (2,-1).
Let the required co-ordinates of the other end of mid-point be (x, y).
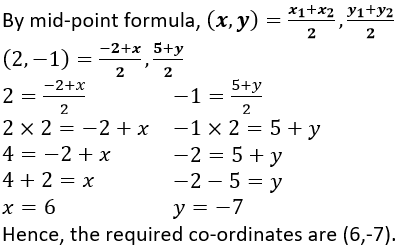
Question 10. A (2, 5), B (1, 0), C (-4, 3) and D (-3, 8) are the vertices of a quadrilateral ABCD. Find the co-ordinates of the mid-points of AC and BD. Give a special name to the quadrilateral.
Solution:
It is given that, A (2, 5), B (1, 0), C (-4, 3) and D (-3, 8) are the vertices of a quadrilateral ABCD.
Here, Co-ordinates of the mid-point of AC,

Question 11. P (4, 2) and Q (-1, 5) are the vertices of a parallelogram PQRS and (-3, 2) are the co- ordinates of the points of intersection of its diagonals. Find the coordinates of R and S.
Solution:
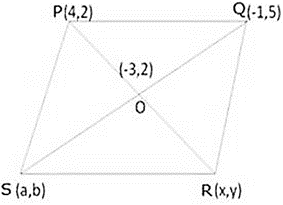
It is given that, the coordinates of P(4,2) and Q(-1,5) and (-3, 2) are the co-ordinates of the points of intersection of its diagonals. Let us assumed that, the co-ordinates of P(4,2) and R(x, y)

Question 12. A (-1, 0), B (1, 3) and D (3, 5) are the vertices of a parallelogram ABCD. Find the co-ordinates of vertex C.
Solution:
Let the coordinates of vertex C be (x,y).
ABCD is a parallelogram.
Mid-point of AC = Mid-point of BD
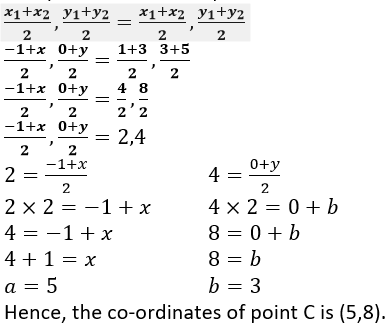
Question 13. The points (2, -1), (-1, 4) and (-2, 2) are mid-points of the sides of a triangle. Find its vertices.
Solution:
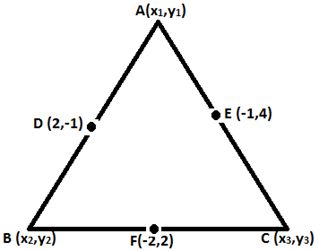
It is given that, the points (2, -1), (-1, 4) and (-2, 2) are mid-points of the sides of a triangle.
Let us assumed that, A(x1,y1), B(x2,y2), C(x3,y3) are the co-ordinates of the vertices of ∆ABC.

By adding equation (1), (3) and (5), we get,
𝑥1 + 𝑥2 + 𝑥1 + 𝑥3 + 𝑥2 + 𝑥3 = 4 + (−2) + (−6)
2𝑥1 + 2𝑥2 + 2𝑥3 = 4 − 2 − 6
2(𝑥1 + 𝑥2 + 𝑥3) = 4 − 2 − 6
2(𝑥1 + 𝑥2 + 𝑥3) = −2
𝑥1 + 𝑥2 + 𝑥3 = −1
Put the value of 𝑥1 + 𝑥2 in above equation,
4 + 𝑥3 = −1
𝑥3 = −1 − 4
𝑥3 = −5
Put the value of 𝑥3 in equation (3)
−2 = 𝑥1 + (−5)
−2 = 𝑥1 − 5
−2 + 5 = 𝑥1
3 = 𝑥1
𝑥1 = 3
Put the value of 𝑥3 in equation (5)
−4 = 𝑥2 + 𝑥3
−4 = 𝑥2 + (−5)
−4 = 𝑥2 − 5
−4 + 5 = 𝑥2
1 = 𝑥2
𝑥2 = 1
By adding equation (2), (4) and (6), we get,
𝑦1 + 𝑦2 + 𝑦1 + 𝑦3 + 𝑦2 + 𝑦3 = −2 + 8 + 4
2𝑦1 + 2𝑦2 + 2𝑦3 = −2 + 12
2(𝑦1 + 𝑦2 + 𝑦3) = 10
𝑦1 + 𝑦2 + 𝑦3 = 5
Put the value of 𝑦1 + 𝑦2 in above equation,
−2 + 𝑦3 = 5
𝑦3 = 5 + 2
𝑦3 = 7
Put the value of 𝑦3 in equation (4),
8 = 𝑦1 + 7
8 − 7 = 𝑦1
𝑦1 = 1
Put the value 𝑦1in equation (6),
−2 = 1 + 𝑦2
−2 = 1 + 𝑦2
−2 − 1 = 𝑦2
−3 = 𝑦2
𝑦2 = −3
Question 14. Points A (-5, x), B (y, 7) and C (1, -3) are collinear (i.e., lie on the same straight line) such that AB = BC. Calculates the values of x and y.
Solution:
It is given that, Points A (-5, x), B (y, 7) and C (1, -3) are collinear such that AB = BC
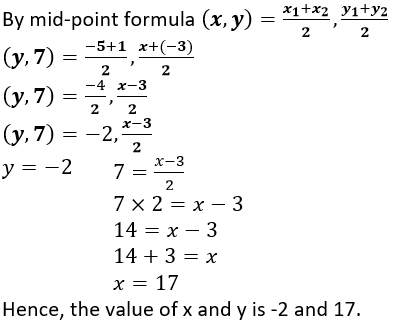
Question 15. Points P (a, -4), Q (-2, b) and R (0, 2) are collinear. If Q lies between P and R, such that PR = 2QR, calculate the values of a and b.
Solution:
It is given that, Points P (a, -4), Q (-2, b) and R (0, 2) are collinear. If Q lies between P and R, such that PR = 2QR.
According to question,
Q lies between P and R, PR=PQ+QR
2QR=PQ+QR
2QR-QR=PQ
QR=PQ
Q is the mid-point,
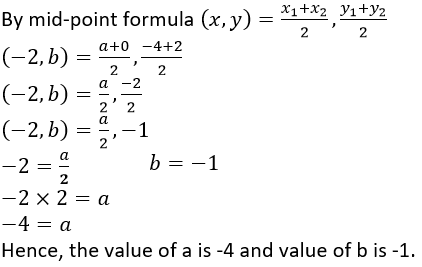
Question 16. Calculate the co-ordinates of the centroid of a triangle ABC, if A = (7, -2), B = (0, 1) and C = (-1, 4).
Solution:
It is given that, co-ordinates of the centroid of a triangle ABC, if A = (7, -2), B = (0, 1) and C = (-1, 4).
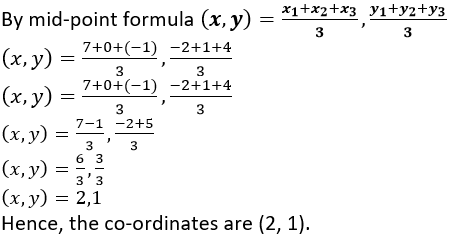
Question 17. The co-ordinates of the centroid of a PQR are (2, -5). If Q = (-6, 5) and R = (11, 8); calculate the co-ordinates of vertex P.
Solution:
Let us assumed that, G be the centroid of DPQR whose coordinates are (2, -5) and let (x,y) be the coordinates of vertex P.
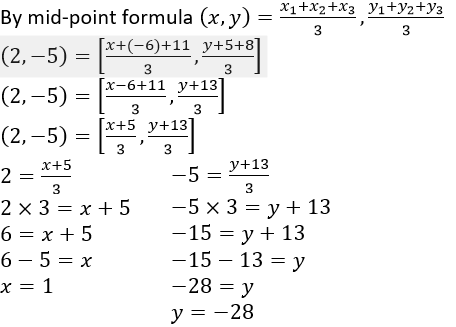
Question 18. A (5, x), B (-4, 3) and C (y, -2) are the vertices of the triangle ABC whose centroid is the origin. Calculate the values of x and y.
Solution:
It is given that, the vertices of the triangle ABC whose centroid is the origin. The co-ordinates at the origin are (0,0).
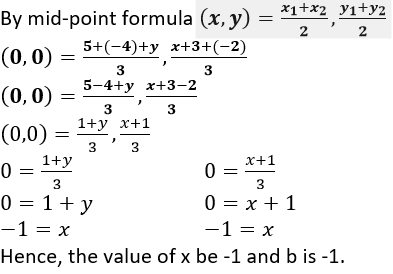
Exercise 13C
Question 1. Given a triangle ABC in which A = (4, -4), B = (0, 5) and C = (5, 10). A point P lies on BC such that BP: PC = 3: 2. Find the length of line segment AP.
Solution:

Question 2. A (20, 0) and B (10, -20) are two fixed points. Find the co-ordinates of a point P in AB such that: 3PB = AB. Also, find the co-ordinates of some other point Q in AB such that AB = 6AQ.
Solution:
It is given that, 3PB=AB

The ratio is 1:5.
It is given that, co-ordinates of A (20, 0) and B (10, -20)
By using section formula

Question 3. A (-8, 0), B (0, 16) and C (0, 0) are the vertices of a triangle ABC. Point P lies on AB and Q lies on AC such that AP: PB = 3: 5 and AQ: QC = 3: 5. Show that: PQ = 3/8 BC.
Solution:
It is given that, the vertices of a triangle are A (-8, 0), B (0, 16) and C (0, 0) and the ratio of AP:PB are 3:5.
By using section formula,

Hence, the co-ordinates of Q are (-5,0).
Distance of PQ,
By distance formula,
We know that the distance formula,
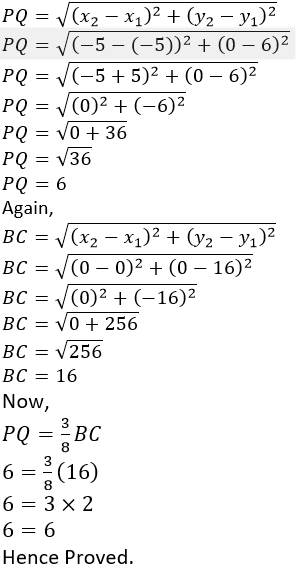
Question 4. Find the co-ordinates of points of trisection of the line segment joining the point (6, -9) and the origin.
Solution:
It is given that, the co-ordinates of point A (6,-9) and B (0,0)
Let us assumed that, Point P divides the line segment in the ratio 1:2 and co-ordinates of P (x, y).
By using section formula,
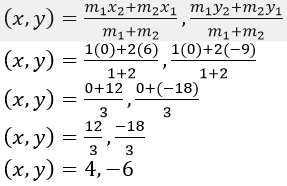
Hence, the co-ordinates of P (4,-6).
Let us assumed that, Point Q divides the line segment in the ratio 2:1 and co-ordinates of Q (x, y).
By using section formula,
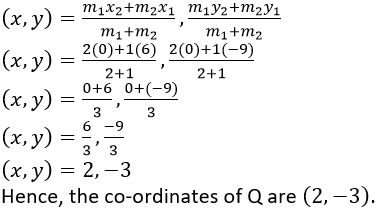
Question 5. A line segment joining A(-1, 5/3) and B (a, 5) is divided in the ratio 1: 3 at P, point where the line segment AB intersects the y-axis.
(i) Calculate the value of ‘a’.
(ii) Calculate the co-ordinates of ‘P’.
Solution:
It is given that, the line segment AB intersects the y-axis at point P
Let us assumed that, the co-ordinates of point P be (0, y) and P divides AB in the ratio 1: 3.
By using section formula,
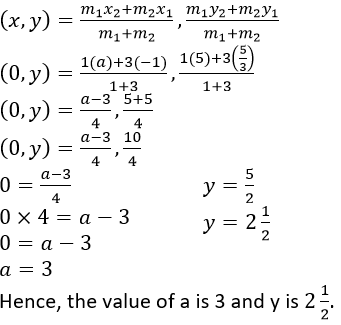
Question 6. In what ratio is the line joining A (0, 3) and B (4, -1) divided by the x-axis? Write the co- ordinates of the point where AB intersects the x-axis.
Solution:
Let the line segment AB intersects the x-axis by point P(x,0) in the ratio K:1.
By using section formula,

Question 7. The mid-point of the segment AB, as shown in diagram, is C (4, -3). Write down the co- ordinates of A and B.
Solution:
A lies on x-axis, co-ordinates of point A(x,0) and B lies on y-axis co-ordinates of point A(0,y).
By mid-point formula,
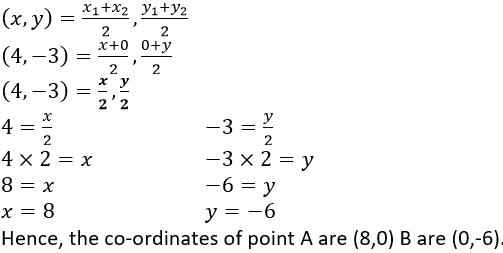
Question 8. AB is a diameter of a circle with centre C = (-2, 5). If A = (3, -7), find
(i) the length of radius AC
(ii) the coordinates of B.
Solution:

Question 9. Find the co-ordinates of the centroid of a triangle ABC whose vertices are: A (-1, 3), B (1, -1) and C (5, 1)
Solution:
It is given that, the co-ordinates of the centroid of a triangle ABC vertices are A (-1, 3), B (1, -1) and C (5, 1).
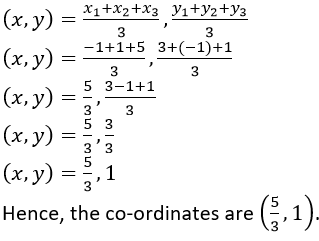
Question 10. The mid-point of the line-segment joining (4a, 2b – 3) and (-4, 3b) is (2, -2a). Find the values of a and b.
Solution:
It is given that the mid-point of the line-segment joining (4a, 2b – 3) and (-4, 3b) is (2,-2a).
By mid-point formula,
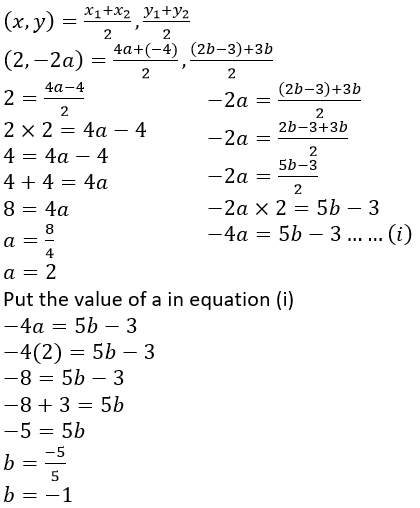
Question 11. The mid-point of the line segment joining (2a, 4) and (-2, 2b) is (1, 2a + 1). Find the value of a and b.
Solution:
It is given that, the mid-point of (2a, 4) and (-2, 2b) is (1, 2a + 1).
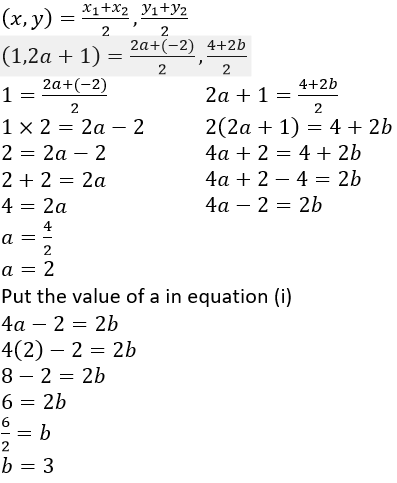
Question 12. (i) Write down the co-ordinates of the point P that divides the line joining A (-4, 1) and B (17, 10) in the ratio 1: 2.
(ii) Calculate the distance OP, where O is the origin.
(iii) In what ratio does the y-axis divide the line AB?
Solution:
(i) It is given that, the co-ordinates of the point P that divides the line joining A (-4, 1) and B (17, 10) in the ratio 1: 2.
By Section formula,


Question 13. Prove that the points A (-5, 4), B (-1, -2) and C (5, 2) are the vertices of an isosceles right- angled triangle. Find the co-ordinates of D so that ABCD is a square.
Solution:
It is given that, the points A (-5, 4), B (-1, -2) and C (5, 2) are the vertices of an isosceles right- angled triangle.

104
𝐴𝐵 = 𝐵𝐶 so, it is a isosceles triangle
We know that, 𝐴𝐵2 + 𝐵𝐶2 = 𝐴𝐶2
𝐴𝐵2 + 𝐵𝐶2 = 𝐴𝐶2
Hence, it is an isosceles right-angles triangle.
If ABCD is a square,
Mid-point of AC = Mid-point of BD
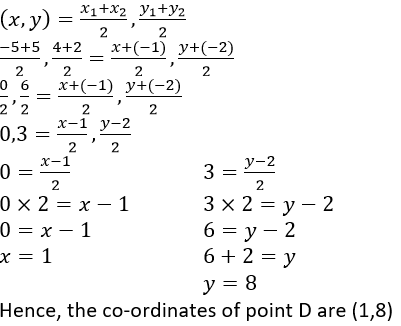
Question 14. M is the mid-point of the line segment joining the points A (-3, 7) and B (9, -1). Find the co-ordinates of point M. Further, if R (2, 2) divides the line segment joining M and the origin in the ratio p: q, find the ratio p: q.
Solution:
It is given that, M is the mid-point of the line segment joining the points A (-3, 7) and B (9, -1).
The co-ordinates of point M are,






