Selina ICSE Class 10 Maths Solutions Chapter 21 Trigonometrical Identities

Question 1.

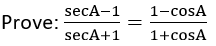
Solution:

Question 2.

Solution:

Question 3.

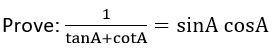
Solution:

Question 4.

Solution:

Question 5. Prove: sin4 A – cos² A = 2sin² A – 1
Solution:
sin⁴ A – cos⁴ A
(sin² A)²-(cos² A)²
(sin² A + cos2 A) – (sin² A – cos² A)
1-(sin² A-cos² A)
sin² A – cos² A
sin² A – (1- sin² A)
2sin² A – 1
LHS = RHS

Question 6. Prove: (1 – tanA)² + (1 + tanA)² = 2sec² A
Solution:
From LHS,
(1-tanA)² + (1 + tanA)²
We know that, (a-b)² = a² + b² – 2ab
(1 + tan² A-2tanA) + (1 + tan² A + 2tanA)
2(1 + tan² A)
2sec² A = RHS

Question 7. Prove: cosec⁴ A-cosec² A=cot4 A + cot² A
Solution:
From LHS,
cosec² A(cosec² A – 1)
From RHS,
cot4 A + cot² A
cot² A(cot² A + 1)
(cosec² A – 1)cosec2 A
LHS = RHS

Question 8. Prove: secA(1 – sinA)(secA + tanA) = 1
Solution

Question 9. Prove: cosecA(1 + cosA)(cosecA – cotA) = 1
Solution:
From LHS
cosecA(1 + cosA)(cosecA – cotA) = 1

Question 10. Prove: sec² A + cosec² A=sec² Acosec² A
Solution:
From LHS
sec² A + cosec² A

Question 11.

Solution:

Question 12. Prove: tan² A – sin² A = tan² Asin² A
Solution:
From LHS,
tan² A – sin² A

Question 13. Prove: cot²A − cos²A = cos²A cot²A
Solution:

Question 14. Prove: (cosecA + sinA)(cosecA − sinA) = cot²A + cos²A
Solution:
From LHS
(cosecA + sinA)(cosecA − sinA)
cosec²A − sin²A
(1 + cot²A) − (1 − cos²A)
1 + cot²A − 1 + cos²A
cot²A + cos²A
LHS = RHS

Question 15. Prove: (secA − cosA)(secA + cosA) = sin²A + tan²A
Solution:
From LHS
(secA − cosA)(secA + cosA)
We know that, (a + b)(a − b) = a² − b²
sec²A − cos²A
(1 + tan²A) − (1 − sin²A)
sin²A − tan²A
LHS = RHS

Question 16. Prove: (cosA + sinA)² + (cosA − sinA)² = 2
Solution:
From LHS
(cosA + sinA)² + (cosA − sinA)²
cos²A + sin²A + 2cosA sinA + cos²A + sis²A − 2cosA sinA
cos²A + sin2A + cos²A + sin2A
2cos²A + 2sin²A
2(cos²A + sin²A)
2 × 1 = 2
LHS = RHS

Question 17. Prove: (cosecA − sinA)(secA − cosA)(tanA + cotA) = 1
Solution:
From LHS
(cosecA − sinA)(secA − cosA)(tanA + cotA)

Question 18.

Solution:

Question 19.

Solution:

Question 20.

Solution:

Question 21. Prove: (sinA + cosecA)² + (cosA + secA)² = 7 + tan²A + cot²A
Solution:
From LHS
(sinA + cosecA)² + (cosA + secA)²
sin²A + cosec²A + 2sinAcosecA + cos²A + sec²A + 2cosAsecA
sin²A + cosec²A + 2 + cos²A + sec²A + 2
sin²A + cosec²A + cos²A + sec²A + 4
sin²A + cos²A + cosec²A + sec²A + 4
1 + cosec²A + sec²A + 4
cosec²A + sec²A + 5
1 + cot²A + 1 + tan²A + 5
cot²A + 1 + tan²A + 6
7 + tan²A + cot²A
LHS = RHS

Question 22. Prove: sec²A. cosec²A = tan2A + cot²A + 2
Solution:

Question 23.

Solution:

Question 24.

Solution:

Question 25.

Solution:

Question 26.

Solution:

Question 27.

Solution:

Question 28.

Solution:

Question 29.

Solution:

Question 30.

Solution:

Exercise 21 B

Question 1. Prove:

Solution:

(v) 2sin²A + cos4A
2sin²A + (1 − sin²A)²
2sin²A + 1 + sin⁴A − 2sin²A
1 + sin⁴A
LHS = RHS

(viii) (1 + tanAtanB)² + (tanA − tanB)²
1 + tan²A tan²B + 2tanAtanB + tan²A + tan²B − 2tanAtanB
1 + tan²A tan²B + tan² A + tan²B
sec²A + tan²B(1 + tan²A)
sec²A + tan²B sec²A
sec²A(1 + tan²B)
sec²A sec²B
LHS = RHS

Question 2. If xcosA + ysinA = m and xsinA − ycosA = n, then prove that x² + y² = m² + n².
Solution:
m² + n²
(xcosA + ysinA)² + (xsinA − ycosA)²
x²cos²A + y²sin²A + 2xysinAcosA + x²sin²A + y²cos²A − 2xysinAcosA
x²cos²A + x²sin²A + y²sin²A + y²cos²A
x²(cos2A + sin²A) + y²(cos²A + sin²A)
x² + y²
Therefore, x² + y² = m² + n²

Question 3. If m = asecA + btanA and n = atanA + bsecA, prove that m² − n² = a² − b²
Solution:
It is given that,
m = asecA + btanA and n = atanA + bsecA
m² − n² = (asecA + btanA)² − (atanA + bsecA)²
a²sec²A + b²tan²A + 2ab secAtanA − (a²tan²A + b²sec²A + 2ab secAtanA)
a²sec²A + b²tan²A + 2ab secAtanA − a²tan²A − b²sec²A − 2ab secAtanA
a²sec²A + b²tan²A − a²tan²A − b²sec²A
a²sec²A − b²sec²A + b²tan²A − a²tan²A
sec²A(a² − b²) + tan²A(a² − b²)
(a² − b²){sec²A + tan²A}
(a² − b²)
Therefore, m² − n² = a² − b²

Question 4. If x = rsinAcosB,y = rsinAsinB and z = r cosA, prove that x² + y² + z² = r²
Solution:
From LHS
(rsinAcosB)² + (rsinAsinB)² + (rcosA)²
r²sin²Acos²B + r²sin²Asin²B + r²cos²A
r²sin²A(cos^2B + sin²B) + r²cos²A
r²sin²A + r²cos²A
r²(sin²A + cos²A)
r²
LHS = RHS

Question 5. If sinA + cosA = m and secA + cosecA = n, prove that n(m²−1) = 2m.
Solution:
It is given that,
sinA + cosA = m and secA + cosecA = n
From LHS,
n(m² − 1)
(secA + cosecA)[(sinA + cosA)²−1]

Question 6. If x = rcosAcosB,y = rcosAsinB and z = rsinA, Prove that x² + y² + z² = r².
Solution:
From LHS
(rcosAcosB)² + (rcosAsinB)² + (rsinA)²
r²cos²Acos²B + r²cos²A sin²B + r²sin²A
r²cos²A (cos²B + sin²B) + r²sin²A
r²cos²A + r²sin²A
r²(cos²A + sin²A)
r²
LHS = RHS

Question 7.

Solution:

Question 1. Without using trigonometric tables, show that:
(i) tan10˚ tan15˚ tan75˚ tan80˚ = 1
(ii) sin42˚ sec48˚ + cos42˚cosec48˚ = 2

Solution:
(i) tan10˚tan15˚tan75˚tan80˚
tan(90˚-80˚)tan(90˚-75˚)tan75˚tan80˚
cot80˚cot75˚tan75˚tan80˚
We know that, cotƟtanƟ = 1
1
LHS=RHS
(ii) sin42˚ sec48˚+cos42˚ cosec48˚ = 2
sin42˚ sec(90˚-42˚) + cos42˚ cosec(90˚-42˚)
sin42˚ cosec42˚ + cos42˚ sec42˚

Question 2. Express each of the following in terms of angles between 0˚ and 45˚:
(i) sin59˚ + tan63˚
(ii) cosec68˚ + cot72˚
(iii) cos74˚ + sec67˚
Solution:
(i) sin59˚ + tan63˚
sin(90˚ − 31˚) + tan(90˚ − 27˚)
cos31˚ + cot27˚
LHS = RHS
(ii) cosec68˚ + cot72˚
cosec(90˚ − 22˚) + cot(90˚ − 18˚)
sec22˚ + tan18˚
LHS = RHS
(iii) cos74˚ + sec67˚
cos(90˚ − 16˚) + sec(90˚ − 23˚)
sin16˚ + cosec23˚
LHS = RHS

Question 3. Show that:

Solution:

Question 4. For triangle ABC, show that:

Solution:

Question 5. A triangle ABC is right angled at B; find the value of

Solution:
It is given that, ABC is a right angled triangle, right angled at B.
A + C = 90˚

Question 6. (i) sinx = sin60˚cos30˚ – cos60˚sin30˚
(ii) sinx = sin60˚cos30˚ + cos60˚sin30˚
(iii) cosx = cos60˚cos30˚ – sin60˚sin30˚
(iv) tanx = tan60˚ – tan30˚/1 + tan60˚ tan30˚
(v) sin²x = 2sin45˚ + cos45˚
(vi) sin3x = 2sin30˚ + cos30˚
(vii) cos⁡(2x – 6˚) = cos² 30˚ – cos² 60˚
Solution:

(vii) cos(2x − 6) = cos²30˚ − cos²60˚
cos(2x − 6) = cos²(90˚ − 60˚) − cos²60˚
cos(2x − 6) = sin²60˚ − cos²60˚
cos(2x − 6) = 1 − 2cos²60˚
cos(2x − 6) = 1 − 2(12)²
cos(2x − 6) = 1 − 2(14)
cos(2x − 6) = 1 − 12
cos(2x − 6) = 12
cos(2x − 6) = cos60˚
2x − 6 = 60˚
2x = 60˚ + 6˚
2x = 66˚
x = 33˚

Question 7. In each case, given below, find the value of angle A, where 0˚≤A≤90˚.
(i) sin(90˚ − 3A).cosec42˚ = 1
(ii) cos(90˚ − A).sec77˚ = 1
Solution:

Question 8. Prove that:

Solution:

Question 9.

Solution:

Question 10. Evaluate:
sin²34˚ + sin²56˚ + 2tan18˚ tan72˚ − cot²30˚
Solution:
sin²34˚ + sin²56˚ + 2tan18˚ tan72˚ − cot²30˚
sin²34˚ + sin²(90˚ − 34˚) + 2tan18˚ tan (90˚ − 72˚) − cot²30˚
sin²34˚ + cos²34˚ + 2tan18˚ cot 18˚ − cot²30˚
(sin²34˚ + cos²34˚) + 2tan18˚(1/tan18˚) − cot²30˚
1 + 2 − (√3)²
3 − 3
0
LHS = RHS

Question 11. Without using trigonometrically tables, evaluate:
cosec² 57° – tan² 33° + cos44° cosec46° – √2 cos45° – tan² 60°
Solution:
cosec² 57° – tan² 33° + cos44° cosec46° – √2 cos45° – tan² 60°
cosec² (90˚-33°) – tan² 33° + cos44° cosec(90˚-44°) – √2 cos45° – tan² 60°
sec33° – tan² 33° + cos44° sec44° – √2 cos45° – tan² 60°
1 + 1 – √2 cos45° – tan² 60°
1 + 1 – √2 (1/√2) – (√3)²
2 – 1 – 3
-2
LHS = RHS

Exercise 21 D

Question 1. Use tables to find sine of:
(i) 21˚
(ii) 34˚ 42’
(iii) 47˚ 32’
(iv) 62˚ 57’
(v) 10˚ 20˚ + 20˚ 45’
Solution:
(i) 21˚
= sin 21˚
= 0.3584
(ii) 34˚ 42’
= sin(34˚ 40’ + 2′)
= 0.5693
(iii) 47˚ 32’
= sin(47˚ 30’ + 2’)
= 0.7373 + 0.0004
= 0.7377
(iv) 62˚ 57’
= sin(62˚ 50’ + 7′)
= 0.8906
(v) 10˚ 20˚ + 20˚ 45’
= sin(30˚ 65’)
= sin(31˚ 5’)
= 0.5150 + 0.0012
= 0.5162

Question 2. Use table to find cosine of:
(i) 2˚ 4’
(ii) 8˚ 12’
(iii) 26˚ 32’
(iv) 65˚ 41’
(v) 9˚ 23’ + 15˚ 54’
Solution:
(i) 2˚ 4’
= cos2˚ 4’
= 0.9994-0.0001
= 0.9993
(ii) 8˚ 12’
= cos8˚ 12’
= 0.9898
(iii) 26˚ 32’
= cos⁡(26˚ 30’ + 2^’)
= 0.8949-0.0003
= 0.8946
(iv) 65˚ 41’
= cos65˚ 41’
= cos(65˚ 36’ + 5′)
= 0.4131-0.0013
= 0.4118
(v) 9˚ 23’ + 15˚ 54’
= cos⁡(9˚ 23’ + 15˚ 54’)
= cos⁡(24˚ 77’)
= cos⁡(25˚ 17’)
= cos⁡(25˚ 12’ + 5′)
= 0.9048-0.0006
= 0.9042

Question 3. Use trigonometrical tables to find tangent of:
(i) 37˚
(ii) 42˚ 18’
(iii) 17˚ 27’
Solution:
(i) 37˚
= tan37˚
= 0.7536
(ii) 42˚ 18’
= tan42˚ 18′
= 0.9099
(iii) 17˚ 27’
= tan⁡(17˚ 27’)
= tan⁡(17˚ 24’ + 3′)
= 0.3134 + 0.0010
= 0.3144

Question 4. Use tables to find the acute angle Ɵ, if the value of sin Ɵ is:
(i) 0.4848
(ii) 0.3827
(iii) 0.6525
Solution:
(i) From the tables,
sin29˚ = 0.4848
Ɵ = 29˚
(ii) From the tables,
sin29˚ = 0.4848
Ɵ = 29˚
(iii) From the table,
sin40˚ 42′ = 0.6521
sinƟ-sin40˚ 42′ = 0.6525-0.6521
sinƟ-sin40˚ 42′ = 0.0004
Ɵ = 40˚ 44′

Question 5. Use tables to find the acute angle Ɵ, if the value of cosƟ is:
(i) 0.9848
(ii) 0.9574
(iii) 0.6885
Solution:
(i) From the table,
cos10˚ = 0.9848
Ɵ = 10˚
(ii) From the table,
cos16˚ 48′ = 0.9574-0.9573 = 0.0001
From the table,
1^’ = 0.0001
Ɵ = 16˚ 48′-1′
Ɵ = 16˚ 47′
(iii) From the table,
cos46˚ 30′ = 0.6885-0.6884 = 0.0001
From the table,
1^’ = 0.0001
Ɵ = 46˚ 30′-1′
Ɵ = 46˚ 29′

Question 6. Use tables to find the acute angle Ɵ, if the value of tan q is:
(i) 0.2419
(ii) 0.4741
(iii) 0.7391
Solution:
(i) From the table,
tan13˚ 36′ = 0.2419
Ɵ = 13˚ 36′
(ii) From the table,
tan25˚ 18′ = 0.4727-0.4727 = 0.0014
From the table
4’ = 0.0014
Ɵ = 25˚ 18′ + 4′
Ɵ = 25˚ 22′
(iii) From the table,
tan36˚ 24′ = 0.7391-0.7373 = 0.0018
From the table
4’ = 0.0018
Ɵ = 36˚ 24′ + 4′
Ɵ = 36˚ 28′

Exercise 21 E

Question 1. If sinA + cosA = p and secA + cosecA = q, the prove that: q(p²−1) = 2p
Solution:
It is given that, q(p²−1) = 2p
(secA + cosecA)[(sinA + cosA)²−1]
We know that (a + b)² = a² + b² + 2ab
= (secA + cosecA)[(sinA + cosA)²−1]
= (secA + cosecA)[sin²A + cos²A + 2sinAcosA − 1]
= (secA + cosecA)[1 + 2sinAcosA−1]
= (secA + cosecA)[2sinAcosA]

Question 2. If x = acosƟ and y = bcotƟ, show that:

Solution:

Question 3. If secA + tanA = p, show that:

Solution:

Question 4. If tan A = ntanB and sinA = msinB, prove that:

Solution:

Question 5. (i) If 2sinA – 1 = 0, show that: sin³A = 3sinA – 4sin³ A
(ii) If 4cos² A – 3 = 0, show that: cos³A = 4cos³ A – 3cosA
Solution:
(i) It is given that, 2sinA – 1 = 0
2sinA = 1
sinA = 1/2
We know that, sin30˚ = 1/2
sinA = sin30˚
A = 30˚
From LHS
sin³A
sin³(30˚)
sin90˚
We know that sin 90˚ = 1
sin90˚ = 1
From RHS
= 3sinA – 4sin³ A
= 3sin(30˚) – 4sin³ A

cosA = cos30˚
A = 30˚
From LHS
cos³A
cos³(30˚)
cos90˚
0
From RHS
= 4cos³ A – 3cosA
= 4cos³ (30˚) – 3cos(30˚)

Question 6.

Solution:

Question 7. If 4cos² A – 3 = 0 and 0˚ ≤ A ≤ 90˚, then prove that:
(i) sin³A = 3sinA – 4sin³ A
(ii) cos³A = 4cos³ A – 3cosA
Solution:
It is given that, 4cos² A – 3 = 0
4cos² A = 3
cos² A = 3/4

cosA = cos30˚
A = 30˚
(i) sin³A = 3sinA – 4sin³ A
From LHS
sin³(30˚)
sin90˚
We know that the value of sin90˚ is 1.
sin90˚ = 1
From RHS,
3sinA – 4sin₃ A
3sin⁡(30˚) – 4sin³ (30˚)

ii) cos³A = 4cos³ A – 3cosA
From LHS
cos³(30˚)
cos90˚
We know that, cos90˚ = 0
cos90˚ = 0
From RHS
= 4cos³ (30˚) – 3cos(30˚)

Question 8. Find A, if 0˚ ≤ A ≤ 90˚ and:
(i) 2cos² A – 1 = 0
(ii) sin³A – 1 = 0
(iii) 4sin²A – 3 = 0
(iv) cos²A – cosA = 0
(v) 2cos²A + cosA – 1 = 0
Solution:

(ii) sin³A – 1 = 0
sin³A = 1
We know that sin90˚ = 1
sin³A = sin90˚
3A = 90˚
A = 90˚/3
A = 30˚

(iv) cos² A – cosA = 0
cosA(cosA – 1) = 0
cosA = 0 or cosA – 1 = 0
cosA = 0 or cosA = 1
We know that, cos90˚ = 0 and cos0˚ = 1
cosA = cos90˚ and cosA = cos0˚
A = 90˚ and A = 0˚
So, the value of A is 90˚ or 0˚
(v) 2cos² A + cosA – 1 = 0
2cos² A + 2cosA – cosA – 1 = 0
2cosA(cosA + 1) – 1(cosA + 1) = 0
(2cosA – 1)(cosA + 1) = 0
2cosA – 1 = 0 or cosA + 1 = 0
2cosA = 1 or cosA = – 1
cosA = 1/2 or cosA = – 1
We know that, cos60˚ = 1/2
cosA = cos60˚
A = 60˚

Question 9. If 0˚<A<90˚; find A, if:

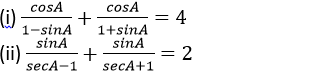
Solution:

Question 10. Prove that: (cosecA – sinA)(secA – cosA)sec² A = tanA
Solution:
From LHS
(cosecA – sinA)(secA – cosA)sec² A

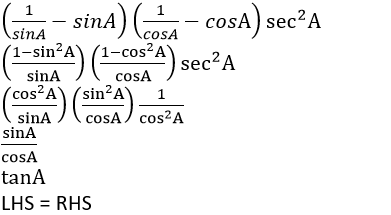
Question 11. Prove the identity (sinƟ + cosƟ)(tanƟ + cotƟ) = secƟ + cosecƟ.
Solution:

Question 12. Evaluate without using trigonometric tables,
sin² 28° + sin² 62° + tan² 38°– cot2 52° + 1/4 sec² 30°
Solution:
sin² 28° + sin² 62° + tan² 38°–cot² 52° + 1/4 sec2 30°
sin2 28° + [sin(90 – 28)°]² + tan² 38° – [cot² (90 – 38)°]² + 1/4 sec² 30°
sin2 28° + cos² 28˚ + tan² 38° – tan² 38 + 1/4 sec² 30°