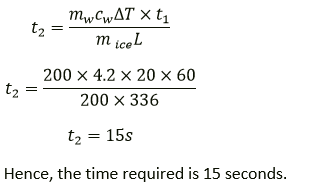Exercise-11A
Question 1. Define the term heat.
Solution:
The thermal energy of a material is the kinetic energy brought on by the random motion of its molecules.
Question 2. Name the S.I. unit of heat.
Solution:
Joule is the S.I. unit of heat (symbol J).
Question 3. Define the term calorie. How is it related to joule (the S.I. unit of heat)?
Solution:
The amount of heat energy needed to elevate 1 g of water from 14.5 °C to 15.5 a.c. is equal to one calorie of heat. Calories equal 4.186 J.
Question 4. Define one kilo-calorie of heat.
Solution:
The amount of heat energy needed to heat 1 kilograms of water from 14.5 °C to 15.5 °C is one kilocalorie.
Question 5. Define temperature and name its S.I. unit.
Solution:
Temperature is the parameter that controls how heat moves between two bodies that are in touch. S.I. unit kelvin (K)
Question 6. Differentiate between heat and temperature.
Solution:

Question 7. Define calorimetry?
Solution:
Calorimetry is the process of measuring the amount of heat.
Question 8. Define the term heat capacity and state its S.I. unit.
Solution:
The quantity of heat energy needed to increase a body’s temperature by 1oC or 1K is known as the heat capacity of the body. S.I. unit is joule per kelvin (JK-1).
Question 9. Define the term specific heat capacity and state its S.I. unit.
Solution:
The amount of heat energy needed to increase a substance’s temperature by 1°C per unit mass is known as its specific heat capacity (or 1K). S.I. unit is joule per kilogram per kelvin (Jkg-1K-1).
Question 10. How is heat capacity of a body related to specific heat capacity of its substance?
Solution:
Heat capacity of a body = Mass × specific heat capacity of its substance.
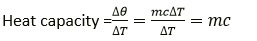
Question 11. Differentiate between heat capacity and specific heat capacity.
Solution:
Heat capacity: It is the quantity of heat energy necessary to increase the temperature by one degree Celsius. Specific heat capacity: It is described as the body’s capacity to store heat per unit of mass.
Question 12. Name a liquid which has the highest specific heat capacity.
Solution:
The substance that can hold the most heat is water.
Question 13. Write the approximate value of specific heat capacity of water in S.I. unit.
Solution:
Specific heat capacity of water = 4200Jkg-1 K-1
Question 14. What do you mean by the following statement?
(i) The heat capacity of a body is 50K-1
(ii) The specific heat capacity of copper is 0.4J g-1 K-1
Solution:
(i) Because a body has a heat capacity of 50K-1 it requires 50 joules of energy to raise its temperature by 1K. .
(ii) Since copper has a specific heat capacity of 0.4Jg-1 K-1 we need to provide 0.4 joules of energy to raise the temperature of one gramme of copper by 1K.
Question 15. Specific heat capacity of a substance A is 3.8 J g-1K-1 and of substance B is 0.4 Jg-1 K-1. Which substance is a good conductor of heat? How did you arrive at your conclusion?
Solution:
Drug B has a lower specific heat capacity than substance A. Therefore, for a given mass and heat energy, B will experience a greater temperature increase than A. Therefore, material B is an excellent heat conductor.
Question 16. Name two factors on which the heat energy liberated by a body on cooling depends.
Solution:
The nature of the substance and temperature change
Question 17. Name three factors on which heat energy absorbed by a body depends and state how does it depend on them
Solution:
The quantity of heat energy absorbed by a body depends on three factors:
(i) Mass of the body – The mass of the material has a direct relationship to the quantity of heat energy needed.
(ii) Nature of material of the body – The quantity of heat energy needed is stated in terms of the substance’s specific heat capacity, which depends on the nature of the substance.
(iii) Rise in temperature of the body – The amount of heat energy needed increases directly as the temperature rises.
Question 18. Write the expression for the heat energy Q received by the substance when m kg of substance of specific heat capacity c Jkg-1 K-1 is heated through Δt° C.
Solution:
The expression for the heat energy Q.
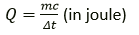
Question 19. Same amount of heat is supplied to two liquid A and B. The liquid A and B The liquid A shows a greater rise in temperature. What can you say about the heat capacity of A as compared to that of B?
Solution:
Liquid A’s heat capacity is lower than liquid B’s. Due to the fact that a material with limited heat capacity increases in temperature more.
Question 20. Two metallic blocks P and Q of masses in ratio 2: 1 are given the same amount of heat. If their temperature rises by the same amount, compare their specific heat capacities.
Solution:
Let CP and Cq be the specific heat capacities of blocks P and Q respectively,
We know that,
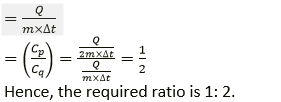
Question 21. What is the principle of method of mixture (or principle of calorimetry)? Name the law on which this principle is based.
Solution:
The mixing method’s guiding premise is: Heat energy obtained by the cold body = Heat energy wasted by the heated body. The law of energy conservation serves as the foundation for this idea.
Question 22. A mass m1 of a substance of specific heat capacity c1 at temperature t1 is mixed with a mass m2 of other substance of specific heat capacity c2 at a lower temperature t2. Deduce the expression for the temperature of the mixture. State the assumption made, if any.
Solution:
When a mass m1 of a material A with specific heat capacity c1 is combined with a mass m2 of a different substance B with specific heat capacity c2 at a higher temperature T2, the combined substance’s ultimate temperature is changed to T.
Fall in temperature of substance A = T1 – T
Rise in temperature of substance B = T – T2
Heat energy lost by A = m1 x c1× fall in temperature
= m1 c1 (T1–T)
Heat energy gained by B = m2 × c2× rise in temperature
=m2 c2 (T2–T)
If no energy lost in the surrounding, then by the principle of mixtures,
Heat energy lost by A = Heat energy gained by B
m1 c1 (T1–T)=m2 c2 (T2–T)

Question 23. Why do the farmers fill their fields with water on a cold winter night?
Solution:
The water in a plant’s tiny capillaries will freeze in the absence of water if the air temperature goes below 0°C on a chilly winter night, causing the veins to rupture since the volume of water expands as it freezes. Plants will subsequently perish, and the crop will be ruined. Farmers saturate their fields with water in order to protect the crop on such chilly nights since water has a high specific heat capacity and prevents temperatures around plants from falling below 0°C.
Question 24. Discuss the role of high specific heat capacity of water with reference to climate in coastal areas.
Solution:
Water has a high specific heat capacity. It is around five times higher than the level of sand. Therefore, a particular amount of water will take approximately five times more heat energy to for the same temperature to rise than a comparable mass of sand. Similar to this, for the same drop in temperature, a specific quantity of water will release approximately five times more heat energy than sand of the same mass would. As a result, under the same circumstances, sand is heated or chilled more quickly than water. As a result, there is a significant temperature differential between the land and the water, leading to the formation of both land- and sea-breezes. This wind makes the climate near the sea shore moderate.
Question 25. Water is used in hot water bottles for fomentation give a reason.
Solution:
Because water has a high specific heat capacity and does not cool down fast, a hot water bottle can supply heat energy for fomentation for an extended period of time.
Question 26. Water property of water makes it an effective coolant?
Solution:
Heat energy from heated machine parts is eliminated by allowing water to flow through pipes surrounding them. Because of its high specific heat capacity, water in pipes may absorb more heat from the environment without experiencing a significant increase in temperature. Water is hence a useful coolant.
Question 27. Give one example where high specific heat capacity of water is used as
(i) Cooling purposes?
(ii) Heat reservoir?
Solution:
(i) Radiator in car.
(ii) To avoid freezing of wine and juice bottles.
Question 28. A liquid X has specific heat capacity higher than the liquid Y.
(i) Which liquid is useful as coolant in car radiators?
(ii) Which liquid is useful as heat reservoir to keep juice bottles without freezing?
Solution:
(i) Liquid X has a larger specific heat capacity than liquid Y. As a result, for a given mass and heat energy, X will have a lower temperature rise than Y. The liquid has to absorb more energy while maintaining a relatively constant temperature when used as a coolant in automotive radiators. Liquid X is therefore perfect for this job.
(ii). Liquid X has a greater specific heat capacity than liquid Y. As a result, for a given mass and heat energy, X will have a lower temperature rise than Y. Before reaching freezing conditions, the liquid must release a significant quantity of heat to act as a heat reservoir to prevent juice bottles from freezing. Consequently, liquid X is excellent.
Question 29. (i) What is a calorimeter?
(ii) Name the material of which it is made of. Give two reasons for using the material stated by you.
(iii) Out of the three metals A, B and C of specific heat 900 J kg-1°C-1, 380 J kg-1°C-1 and 460 J kg-1°C-1 respectively, which will you prefer for calorimeter? Given reason
(iv) How is the loss of heat due to radiation minimized in a calorimeter?
Solution:
(i) A calorimeter is a cylindrical container used to calculate how much heat is transferred when one body interacts with another.
(ii) It is composed of thin copper sheet:-
(a) Because copper is an excellent heat conductor, the vessel quickly picks up the temperature of its contents.
(b) Since copper has a low specific heat capacity, a calorimeter’s heat capacity is also low, and little heat energy is extracted from the calorimeter’s contents to determine the temperature of those contents.
(iii) The calorimeter should have a low heat capacity, thus it is best to choose the metal with the lowest specific heat capacity out of the three.
(iv) Radiation loss can be reduced by cleaning the vessel’s exterior and interior surfaces.
Question 30. Why is the base of a cooking pan generally made thick?
Solution:
A cooking pan’s thermal capacity increases when the base is made thick, and the food is given enough heat energy at a low temperature to cook properly. Additionally, after cooking, it keeps the meal warm for a very long period.
Exercise–11A
Multiple Choice Types
Question 1 The S.I. unit of heat capacity is :
a) J kg-1
b) J K-1
c) J kg-1 K-1
d) cal °C-1
Solution: b) J K-1
Question 2. The S.I. unit of specific heat capacity is:
a) J kg-1
b) J K-1
c) J kg-1 K-1
d) kilocal kg-1 °C-1
Solution: c) J kg-1 K-1
Question 3. The specific heat capacity of water is :
a) 4200 J kg-1 K-1
b) 420 J g-1 K-1
c) 0.42 J g-1 K-1
d) 4.2 J kg-1 K-1
Solution: a) 4200 J kg-1 K-1
Exercise–11A
Numericals
Question 1. By imparting heat to a body its temperature rises by 15° C. what is the corresponding rise in temperature on Kelvin scale?
Solution:
The size of 1 degree on the Kelvin scale is the same as the size of 1 degree on the Celsius scale. Thus, the difference (or change) in temperature is the same on both the Celsius and Kelvin scales. Hence, the corresponding rise in temperature on the Kelvin scale will be 15K.
Question 2. (a) Calculate the heat capacity of a copper vessel of mass 150g if the specific heat capacity of copper is `410 Jkg-1 K-1.
(b) How much heat energy will be required to increase the temperature of the vessel in part (a) from 25°C to 35°C?
Solution:
(i) It is given that,
Mass of copper vessel = 150 g = 0.15 kg
the specific heat capacity of copper = 410 Jkg-1 K-1
0.15kg×410 Jkg-1 K-1
61.5 Jkg-1 K-1
Change in temperature = (35-25)°C = 10°C = 10K
(ii) Energy required to increase the temperature of vessel
ΔQ = mc×ΔT
ΔQ = 0.15 × 410×10
ΔQ = 615J
Question 3. A piece of iron of mass 2.0 kg has a thermal capacity of 966JK-1. Find:
(i) Heat energy needed to warm it by 15°C
(ii) Its specific heat capacity in S.I unit.
Solution:
(i) We know that heat energy needed to raise the temperature by 15° is = heat capacity × change in temperature. Heat energy required = 966JK-1 ×15K = 14490K
(ii) We know that specific heat capacity is = heat capacity/ mass of substance so specific heat capacity is
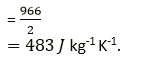
Question 4. Calculate the amount of heat energy required to raise the temperature of 100 g of copper from 20°C to 70°C. Specific heat capacity of copper = 390 Jkg-1 K-1
Solution:
Mass of copper m = 100 g = 0.1 kg
Change of temperature Δt = (70 − 20) °C
Specific heat of capacity of copper = 390 Jkg-1 K-1
Amount of heat required to raise the temperature of 0.1 kg of copper is
Q = m × Δt × c
Q = 0.1 × 50 × 390
Q = 1950 J
Question 5. 1300 J of heat energy is supplied to raise the temperature of 0.5 kg of lead from 20° C to 40°C. Calculate the specific heat capacity of lead
Solution:
Heat energy supplied = 1300 J
Mass of lead = 0.5 kg
Change in temperature = (40-20)°C = 20 °C (or 20 K)
Specific heat capacity of lead
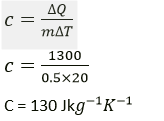
Question 6. Find the time taken by a 500 W heater to raise the temperature of 50 kg of material of specific heat capacity 960 Jkg-1 K-1 from 18°C to 38° C. assume that all the heat energy supplied by the heater is given to the material.
Solution:
Specific heat capacity of material c =960 Jkg-1 K-1
Change in temperature ΔT = (38 − 18)°C = 20°C (or 20 K)
Power of heater P = 500 W
ΔQ = mcΔT
ΔQ = 50 × 960 × 20
Time taken by a heater to raise the temperature of material
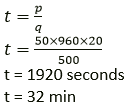
Question 7. An electric heater of power 600W raises the temperature of 4.0kg of a liquid from 10.0 ℃ to 15.0 ℃, 100s. Calculate: (i) the heat capacity of 4.0 kg of liquid, (ii) the specific heat capacity of the liquid.
Solution:
Power of heater P = 600 W
Mass of liquid m = 4.0 kg
Change in temperature of liquid = (15 − 10) °C = 5 °C(or 5 K)
Time taken to raise its temperature = 100s
Heat energy required to heat the liquid ΔQ = mcΔT
And
ΔQ = P × t
ΔQ = 600 × 100
ΔQ = 60000J
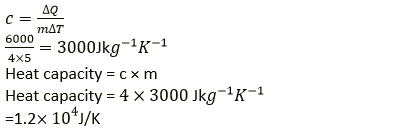
Question 8. 0.5 kg of lemon squash at 30° C is placed in a refrigerator which can remove heat at an average rate of 30Js-1. How long will it take to cool the lemon squash to 5°C? Specific heat capacity of squash = 4200 Jkg-1 K-1
Solution:
Change in temperature= 30 − 5 = 25 K.
ΔQ = mcΔT
ΔQ = 0.5×4200×25=52500J
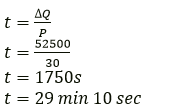
Question 9. A mass of 50g of a certain metal at 150° C is immersed in 100g of water at 11° C. The final temperature is 20° C. calculate the specific heat capacity of the metal. Assume that the specific heat capacity of water is 4.2 J g-1 K-1.
Solution:
Heat liberated by metal = m×s×∆t
=50×s×(150-20)
Heat absorbed by water = mw×sw×∆t
=100×4.2×(20-11)
Heat energy lost= heat energy gained
50×s×(150-20)=100×4.2×(20-11)
S=0.58Jg-1 K-1.
Question 10. 45 g of water at 50°C in a beaker is cooled when 50 g of copper at 18° C is added to it. The contents are stirred till a final constant temperature is reached. Calculate this final temperature. The specific heat capacity of copper is 0.39 Jkg-1 K-1 and that of water is 4.2 Jkg-1 K-1 State the assumption used.
Solution:
Mass of water (m1) = 45 g
Temperature of water (T1) = 50 °C
Mass of copper (m2) = 50 g
temperature of copper (T2) = 18°C
Final temperature (T) =?
The specific heat capacity of the copper c2 = 0.39 J/g/K
The specific heat capacity of water c1 = 4.2 J/g/K
m1 c1 (T1-T) = m2 c2 (T-T2)
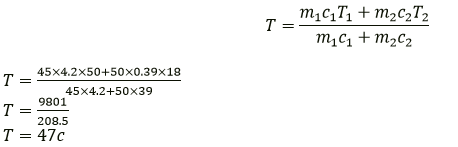
Question 11. 200 g of hot water at 80°C is added to 300 g of cold water at 10°C. Neglecting the heat taken by the container, calculate the final temperature of the mixture of water. Specific heat capacity of water = 4200J g-1 K-1.
Solution:
Mass of hot water (m1) = 200g
Temperature of hot water (T1) = 80°C
Mass of cold water (m2) = 300g
Temperature of cold water (T2) =10°C
Final temperature (T) =?
m1 c1 (T1-T) = m2 c2 (T-T2)
c1 = c2

Question 12. The temperature of 600 g of cold water rises by 15°C when 300 g of hot water at 50°C is added to it. What was the initial temperature of the cold water?
Solution:
It is given that,
Mass of hot water (m1) = 300g
Temperature (T1) = 50°C
Mass of cold water (m2) = 600g
Change in temperature of cold water (T − T2) = 15°C
Final temperature = T°C
The specific heat capacity of water is c.
m1 c1 (T1-T) = m2 c2 (T-T2)
300(50-T) = 600(15)
T = 20°C
Final temperature = 20°c
Change in temperature = 15°C
Initial temperature of cold water = 20°C – 15°C
Initial temperature of cold water = 5°C.
Question 13. 1.0 kg of water is container in a 1.25 kW kettle Calculate the time taken for the temperature of water to rise from 25° C to its boiling point 100°C. Specific heat capacity of water = 4.2 J g-1 K-1.
Solution:
Mass of water = 1000 g.
Change in temperature = 100°C-25°C
= 75°C (or 75K)
Amount of heat energy required to raise temperature = 1000×4.2×75
= 315000 J.
Time taken to raise the temperature, T = 4 min 12 seconds.
Exercise–11B
Question 1. (i) What do you understand by the change of phase of a substance?
(ii) Is there any change in temperature during the change of phase?
(iii) Does the substance absorb or liberate any heat energy during the change of phase?
(iv) What is the name given to the energy absorbed during a phase change?
Solution:
(i) The phase change of a material refers to the process of changing from one state to another while maintaining a constant temperature.
(ii) The temperature remains constant during the phase shift.
(iii) The material does indeed absorb or release heat during the phase shift.
(iv) The energy absorbed during a phase change is Latent heat
Question 2. (i) A substance changes from its solid state to the liquid state when heat is supplied to it name the process.
(ii) What name is given to heat observed by the substance.
(iii) How does the average kinetic energy of the molecules of the substance change.
Solution:
(i) Melting.
(ii) Latent heat of melting.
(iii) The average kinetic energy of the molecules remains constant since there is no temperature change.
Question 3. A substance undergoes (i) a change in its temperature, (ii) a change in its phase without change in its temperature. In each case, state the change in energy of molecules of the substance.
Solution:
(i) Average kinetic energy of molecules changes.
(ii) Average potential energy of molecules changes.
Question 4. (i) How does the average kinetic energy?
(ii) How does the average potential energy of molecules of a substance change during its change in phase at a constant temperature?Solution:
(i) Average kinetic energy does not change.
(ii) Average potential energy increases.
Explanation: When a substance is heated to a constant temperature (i.e., during a phase shift), the heat generated gives the vibrating molecules the potential energy they need to overcome the force of attraction between molecules and move around freely. This indicates that the material transforms. However, because this heat does not raise the molecules’ kinetic energy, there is no temperature increase as a result of a substance’s change in phase. Latent heat is the heat that is given to the substance and is used to change the state of matter without increasing the temperature.
Question 5. State the effect of presence of impurity on the melting point of ice. Give one use of it.
Solution:
The presence of impurities in ice lowers its melting point.
Use: To create a freezing combination by combining ice and salt. Ice creams are made using this freezing combination.
Question 6. State the effect of increase of pressure on the melting point of ice.
Solution:
The reduction in pressure causes the melting point of ice to rise. Every additional atmosphere of pressure causes a 0.0072°C drop in the melting point of ice.
Question 7. The diagram in Fig 11.12 below shows the change of phase of a substance on a temperature time graph.
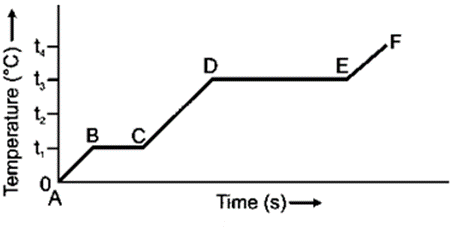
(a) What do the parts AB, BC, CD and DE represent?
(b) What are the melting points of the substance?
(c) What is the boiling point of the substance?
Solution:
(a) The AB section depicts the rise in temperature of the solid from 0 to T1, the BC part depicts the melting at T1, the CD part depicts the rise in temperature of the liquid from T1 to T3, and the DE part depicts the boiling at T3.
(b) T1˚C.
(c) T3˚C.
Question 8. 1 kg of ice at 0o is heated at constant rate and its temperature is recorded after every 30 s till steam is formed at 100˚C. Draw a temperature time graph to represent the change of phase.
Solution:
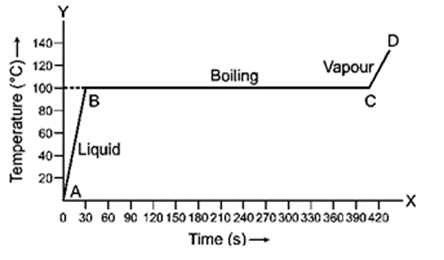
Question 9. Explain the term boiling?
(ii) Explain the term boiling point?
Solution:
(i) Boiling is the process of heating a liquid to a consistent temperature and converting it to a gas.
(ii) Boiling point: The boiling point of a liquid is the specific temperature at which vaporisation takes place.
Question 10. How is the volume of water affected when it boils at 100℃?
Solution:
When water reaches 100˚C, its volume will expand.
Question 11. How is the boiling point of water affected when some salt is added to it?
Solution:
As salt is added, the boiling point of water rises
Question 12. What is the effect of increase in pressure on the boiling point of a liquid?
Solution:
As pressure rises, a liquid’s boiling point rises as well.
Question 13. Water boils at 120 °C in a pressure cooker. Explain the reason
Solution:
• A liquid’s boiling point rises with increasing pressure and falls with decreasing pressure.
• Pure water has a boiling point of 100 °C at one atmosphere of pressure (760 mm Hg).
• Since steam cannot escape from a pressure cooker, the water boils at 120 to 125 degrees Celsius as a result of the increased pressure.
Question 14. Write down the approximate range of temperature at which water boils in a pressure cooker.
Solution:
Water boils in a pressure cooker at a temperature between 120°C and 125°C.
Question 15. It is difficult to cook vegetables on hills and mountains. Explain the reason.
Solution:
This is due to low air pressure at high elevations, which causes water’s boiling point to fall and cease to deliver the necessary thermal energy for cooking.
Question 16. Complete the following sentence:
(i) When ice melts, its volume _________
(ii) Decrease in pressure over ice ________ its melting point.
(iii) Increase in pressure _________ the boiling point of water.
(iv) A pressure cooker is based on the principle that boiling point of water increases with the _________
(v) The boiling point of water is defined as _________
(vi) Water can be made to boil at 115°C by ___________ Pressure over its surface
Solution:
(i) When ice melts, its volume decreases.
(ii) Decrease in pressure over ice increases its melting point
(iii) Increase in pressure increases the boiling point of water
(iv) A pressure cooker is based on the principle that boiling point of water increases with the increase in pressure.
(v) The boiling point of water is defined as the constant temperature at which water changes to steam.
(vi) Water can be made to boil at 115°C by increasing pressure over its surface.
Question 17. What do you understand by the term latent heat?
Solution:
The heat energy exchanged during a phase shift is thought to remain buried inside the substance and is referred to as latent heat since it does not externally appear as an increase or decrease in temperature.
Question 18. Define the term specific latent heat of fusion of ice state its S.I unit.
Solution:
The specific latent heat of fusion of ice is the amount of heat needed to melt a unit mass of ice at 0°C (the melting point).
Its S.I. unit is JKg-1
Question 19. Write the approximate value of specific latent heat of ice.
Solution:
Specific latent heat of ice: 336000 JKg-1
Question 20. The specific latent heat of fusion of ice is 336Kg-1. Explain the meaning of its statement.
Solution:
In order for 1 g of ice to turn into water at 0°C, 360 J of heat energy must be absorbed.
Question 21. 1 g ice of 0℃ melts to form 1 g water at 0℃. State whether the latent heat is absorbed or given out by ice.
Solution:
Ice takes in latent heat.
Question 22. Which has more heat: 1 g ice at 0℃ or 1g water 0℃? Give reason.
Solution:
In comparison to 1 g of ice at 0°C, 1 g of water has greater heat. This is due to the fact that water at 0°C requires ice to absorb 360 J of heat energy.
Question 23. (a) Which requires more heat: 1 g ice at 0℃ or 1 g water at 0℃ to raise its temperature to 10℃?
(b) Explain your answer in part (a).
Solution:
(a) 1g of ice at 0˚C needs more heat because melting ice would demand greater heat energy.
(b) To create 1g of water at 0˚C from 1g of ice at 0˚C, 336 J of heat must first be absorbed.
Question 24. Ice cream appears coder to the mouth than water at 0℃. Give reason.
Solution:
This is due to the fact that melting 1 g of ice at 0°C requires 336 J of heat energy from the mouth. As a result, mouth loses 336 J more heat energy when 1 g of ice is present at 0°C than when 1 g of water is present. As a result, 1 g of ice produces more cooling than 1 g of water does at the same temperature.
Question 25. Why do bottled soft drinks get cooled, more quickly by the ice cubes than by the iced water, both at 0℃?
Solution:
This is so that 1 g of ice at 0˚C may melt into water at 0˚C, which requires 336 J of heat energy from the bottle. As a result, the bottle loses 336 J more heat energy when 1 g of ice is present at 0˚C than when 1 g of frozen water is present. Therefore, bottled soft drinks get cooled, more quickly by the ice cubes than by iced water.
Question 26. It is generally cold after a hail-storm then during and before the hail storm. Give reason.
Solution:
The ice takes the heat energy needed for melting from the environment after the hailstorm, which causes the surrounding temperature to drop further and makes us feel colder.
Question 27. The temperature of the surrounding starts falling when ice in a frozen lake starts melting. Give reason.
Solution:
The cause is because the nearby atmosphere provides the thermal energy needed to defrost the frozen lake. As a result, the area’s temperature drops and it gets exceedingly cold.
Question 28. Water in lakes and ponds do not freeze at once in cold countries. Give reason.
Solution:
With a value of roughly 336 J Kg-1, the specific latent heat of fusion of ice is suitably high. The water in the lakes and ponds must shed a significant amount of heat to the surroundings before freezing. Since water is a poor conductor of heat, any covering of ice that has developed on it will likewise stop heat loss from lake water. Consequently, lakes and ponds do not freeze in cold areas.
Question 29. Explain the following:
(i) The surrounding becomes pleasantly warm when water in a lake starts freezing in cold countries?
(ii) The heat supplied to a substance during it change of state, does not cause any rise in its temperature.
Solution:
(i) Because the specific latent heat of fusion of ice is sufficiently high, a significant amount of heat must be released when lake water freezes, resulting in a nice rise in ambient temperature. (ii) Due to the latent heat of phase shift, which is only needed to change the phase, heat applied to a substance during a change in state has no effect on temperature.
Exercise–11B
Multiple Choice Types
Question 1. The S.I. unit of specific latent heat is:
a) cal g-1
b) cal g-1 K-1
c) J kg-1
d) J kg -1 K-1
Solution: c) J kg-1
Question 2. The specific latent heat of fusion of water is:
a) 80 cal g-1
b) 2260 Jg-1
c) 80 Jg-1
d) 336 Jkg-1
Solution: a) 80 cal g-1
Exercise–11B
Numericals
Question 1. 10g of ice at 0℃ absorbs 5460 J of heat energy to melt and change to water at 50℃. Calculate the specific latent heat of fusion of ice. Specific heat capacity of water is 4200JKg-1 K-1
Solution:
Mass of ice = 10g = 0.01kg
Amount of heat energy absorbed, Q = 5460J
Specific latent heat of fusion of ice = ?
Specific heat capacity of water = 4200JKg-1 K-1
Amount of heat energy required by 10g (0.01kg) of water at 0°C to raise its temperature by 50°C = 0.01 × 4200 × 50
= 2100J.
Let Specific latent heat of fusion of ice = L Jg-1
Then,
Q = mL + mcΔT
5460J = 10×L + 2100J
L = 336Jg-1
Question 2. How much heat energy is released when 5.0 of water at 20℃ changes into ice at 0℃? Take specific heat capacity of water = 4.2 JKg-1 K-1 Specific latent heat of fusion of ice 336 Jg-1
Solution:
Mass of water m = 5.0 g
Specific heat capacity of water c = 4.2 JKg-1 K-1
Specific latent heat of fusion of ice L = 336 Jg-1
Amount of heat energy released when 5.0 g of water at 20°C changes into water at 0°C
= 5×4.2 ×20
= 420 J.
Amount of heat energy released when 5.0g of water at 0°C changes into ice at 0°C
= 5 × 336J
= 1680J.
Total amount of heat released = 1680J + 420J = 2100J.
Question 3. A molten metal of mass 150 g is kept at its melting point 800℃. When it is allowed to freeze at the same temperature, it gives out 75,000 J of heat energy.
(a) What is the specific latent heat of the metal?
(b) If the specific heat capacity of metal is 200 JKg-1 K-1, how much additional heat energy will the metal give out in cooling to – 50 ℃?
Solution:
Mass of metal = 150 g
Specific latent heat of metal
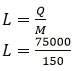
L = 500Jg-1
Specific heat capacity of metal is 200 JKg-1 K-1
Change in temperature = 800-(-50)
Change in temperature = 850°C (or 850 K).
ΔQ = mc×ΔT
ΔQ = 0.15×200×850
ΔQ = 25500J
Question 4. A refrigerator converts 100g of water at 20℃ to ice at –10℃ in 73.5min. Calculate the average the rate of heat extraction in watt. The specific heat capacity of water is 4.2JKg-1 K-1 Specific latent heat of ice is 336 J g-1 and the specific heat capacity of ice if 2.1JKg-1 K-1.
Solution:
Amount of heat released when 100g of water cools from 20o to 0°C = 100 × 20 × 4.2 = 8400J.
Amount of heat released when 100g of water converts into ice at 0°C = 100 × 336 = 33600J.
Amount of heat released when 100g of ice cools from 0°C to -10°C = 100 × 10 × 2.1 = 2100J. Total amount of heat = 8400 + 33600 + 2100 = 44100J.
Time taken = 73.5min = 4410s.
Average rate of heat extraction (power)
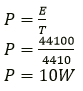
Question 5. In an experiment, 17g of ice is used to bring down the temperature of 40 g of water at 34℃ to its freezing temperature. The specific heat capacity of water is 4.2 JKg-1 K-1 Calculate the specific latent heat of ice. State one important assumption made in the above calculation.
Solution:
Mass of ice m1 = 17 g
Mass of water m2 = 40 g.
Change in temperature = 34 – 0 = 34K
Specific heat capacity of water is 4.2 JKg-1 K-1
Assuming there is no loss of heat, heat energy gained by ice (latent heat of ice), Q= heat energy released by water Q = 40 × 34 × 4.2 = 5712 J
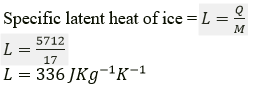
Question 6. Find the result of mixing 10 g of ice at – 10℃ with 10 g of water at 10℃. Specific heat capacity of ice = 2.1 JKg-1 K-1 specific latent heat of ice = 336 jg-1 specific heat capacity of water = 4.2 JKg-1 K-1
Solution:
Let whole of the ice melts and let the final temperature of the mixture be T°C.
Amount of heat energy gained by 10g of ice at -10°C to raise its temperature to 0°C
= 10×10×2.1
= 210J
Amount of heat energy gained by 10g of ice at 0°C to convert into water at 0°C
= 10×336
= 3360J
Amount of heat energy gained by 10g of water (obtained from ice) at 0˚C to raise its temperature to T°C = 10×4.2×(T-0) = 42T
Amount of heat energy released by 10g of water at 10°C to lower its temperature to T°C = 10 × = 4.2×(10-T)
= 420-42T
Heat energy gained = Heat energy lost
T = 210+3360+42T
T = 420-42T
T = -37.5°C
This cannot be true because water cannot exist at this temperature. So whole of the ice does not melt. Let m gm of ice melts. The final temperature of the mixture becomes 0°C. So, amount of heat energy gained by 10g of ice at -10°C to raise its temperature to 0°C
= 10×10×2.1
= 210J
Amount of heat energy gained by m gm of ice at 0°C to convert into water at 0°C
= m×336
= 336mJ
Amount of heat energy released by 10g of water at 10°C to lower its temperature to 0°C = 10×4.2×(10-0)
= 420
Heat energy gained = Heat energy lost 210 + 336m = 420 m = 0.625 gm.
Question 7. A piece of ice of mass 40 g is added to 200 g of water at 50℃, Calculate the final temperature of water when all the ice has melted. Specific heat capacity of water = 4200 JKg-1 K-1 and specific latent heat of fusion of ice = 336×103 JKg-1
Solution:
Let us assumed that,
Final temperature of water when all the ice has melted = T°C.
Amount of heat lost when 200g of water at 50°C cools to T°C
= 200×4.2×(50-T)
= 42000 – 840T
Amount of heat gained when 40g of ice at 0oC converts into water at 0˚C. = 40 × 336J = 13440J
Amount of heat gained when temperature of 40g of water at 0˚C rises to T˚C
= 40×4.2×(T-0)
= 168T
We know that,
Amount of heat gained = amount of heat energy lost.
13440+168T = 42000-840T
168T+840T = 42000 –13440
1008T = 28560

Question 8. 250 g of water at 30℃ is contained in a copper vessel of mass 50g. Calculate the mass of ice required to bring down the temperature of the vessel and its contents to 5℃. Given: specific latent heat of fusion of ice = 336×103 JKg-1 specific heat capacity of copper = 400 JKg-1 K-1 specific heat capacity of water = 4200 JKg-1 K-1
Solution:
Mass of copper vessel m1 = 50 g.
Mass of water contained in copper vessel m2 = 250 g.
Mass of ice required to bring down the temperature of vessel = m
Final temperature = 5°C.
Amount of heat gained when ‘m’ g of ice at 0°C converts into water at 0°C = m × 336 J
Amount of heat gained when temperature of ‘m’ g of water at 0°C rises to 5°C = m × 4.2 × 5
Total amount of heat gained = m × 336 + m × 4.2 × 5
Amount of heat lost when 250 g of water at 30°C cools to 5°C = 250 × 4.2 × 25 = 26250J
Amount of heat lost when 50 g of vessel at 30°C cools to 5°C = 50 × 0.4 × 25 = 500 J
Total amount of heat lost = 26250 + 500 = 26750 J
We know that amount of heat gained = amount of heat lost
m×336+m×4.2×5 = 26750
357m = 26750
m = 26750/357
m = 74.93g
Hence, mass of ice required is 74.93 g.
Question 9. 2kg of ice melts when water at 100℃ is poured in a hole drilled in a block of ice. What mass of water was used? Given: Specific heat capacity of water = 400JKg-1 K-1 Lice = 336×103 JKg-1.
Solution:
Since the whole block does not melt and only 2 kg of it melts, so the final temperature would
be 0 °C. Amount of heat energy gained by 2 kg of ice at 0°C to convert into water at 0°C
= 2× 336000
= 672000J
Let us assumed that,
Amount of water poured = m kg.
Initial temperature of water = 100°C.
Final temperature of water = 0°C.
Amount of heat energy lost by m kg of water at 100oC to reach temperature 0°C
= m×4200×100 = 420000mJ
We know that heat energy gained = heat energy lost.
672000J = m × 420000J
m = 672000/420000
m = 1.6kg
Question 10. Calculate the total amount of heat energy required to convert 100g of ice at −10℃ completely into water at 100℃. Specific heat capacity of ice = 2.1 JKg-1 K-1 specific heat capacity of water = 4.2 JKg-1 K-1, specific latent heat of ice = 336 jg-1
Solution:
Amount of heat energy gained by 100 g of ice at -10°C to raise its temperature to 0°C
= 100×2.1×10
= 2100 J
Amount of heat energy gained by 100 g of ice at 0°C to convert into water at 0°C
= 100×336
= 33600J
Amount of heat energy gained when temperature of 100 g of water at 0°C rises to 100°C
= 100×4.2×100
= 42000J
Total amount of heat energy gained is
= 2100 + 33600 + 42000
= 77700 J
= 7.77×104
Question 11. The amount of heat energy required to convert 1 kg of ice at – 10℃ to water at 100℃ is 7,77,000 J. Calculate the specific latent heat of ice. Specific heat capacity if ice = 2100 JKg-1 K-1, Specific heat capacity of water = 4200 JKg-1 K-1
Solution:
Amount of heat energy gained by 1kg of ice at −10°C to raise its temperature to 0°C
= 1×2100×10
= 21000J
Amount of heat energy gained by 1kg of ice at 0°C to convert into water at 0°C = L
Amount of heat energy gained when temperature of 1kg of water at 0oC rises to 100°C
= 1×4200×100
= 420000J
Total amount of heat energy gained = 21000 + 420000 + L = 441000 + L.
Given that total amount of heat gained is = 777000J.
So,
441000 + L = 777000
L = 777000 – 441000
L = 336000 JKg-1
Question 12. 200 g of ice at 0 °C converts into water at 0 °C in 1 minute when heat is supplied to it at a constant rate. In how much time, 200 g of water at 0 °C will change to 20 °C? Take specific latent heat of ice = 336 J g-1.
Solution:
Mass of ice, mice = 200 g
Time for ice to melt, t1 = 1 min = 60 s
Mass of water, mw = 200 g
Temperature change of water, ΔT = 20 °C
Rate of heat exchange is constant. So, power required for converting ice to water is same as the power required to increase the temperature of water.